数字电子技术-第四章课后习题答案-(江晓安等编).doc

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：13.57M 资料格式：doc 举报版权申诉

liulicaixia-10026327-4744302543354257664.doc.pdf-第1页.png

第1页 / 共27页

liulicaixia-10026327-4744302543354257664.doc.pdf-第2页.png

第2页 / 共27页

liulicaixia-10026327-4744302543354257664.doc.pdf-第3页.png

第3页 / 共27页

liulicaixia-10026327-4744302543354257664.doc.pdf-第4页.png

第4页 / 共27页

liulicaixia-10026327-4744302543354257664.doc.pdf-第5页.png

第5页 / 共27页

liulicaixia-10026327-4744302543354257664.doc.pdf-第6页.png

第6页 / 共27页

liulicaixia-10026327-4744302543354257664.doc.pdf-第7页.png

第7页 / 共27页

liulicaixia-10026327-4744302543354257664.doc.pdf-第8页.png

第8页 / 共27页

文本预览

第四章组合逻辑电路 1. 解： (a)(b)是相同的电路，均为同或电路。 2. 解：分析结果表明图(a)、(b)是相同的电路，均为同或电路。同或电路的功能：输入相同输出为“1”；输入相异输出为“0”。因此，输出为“0”(低电平)时，输入状态为 AB＝01 或 10 3. 由真值表可看出，该电路是一位二进制数的全加电路，A 为被加数，B 为加数，C 为低位向本位的进位，F1 为本位向高位的进位，F2 为本位的和位。 4. 解：函数关系如下： ABSF  3  SBBAS 2 1   BS 0  A 将具体的 S 值代入，求得 F 值，填入表中。

SSSS 3 12 0                 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111     )  B  AB   ( BA   AB BABA AB   AA BABA BABA 1  1  1  101   F F F F BAAABAABAF BABABABABABAF BABAF 0 BAF  BAA AB F  F BABABA AB  F BBA AB   0 F AB AB   0 AAF  BABAAF  BABABAAF AF       0 A   AB 

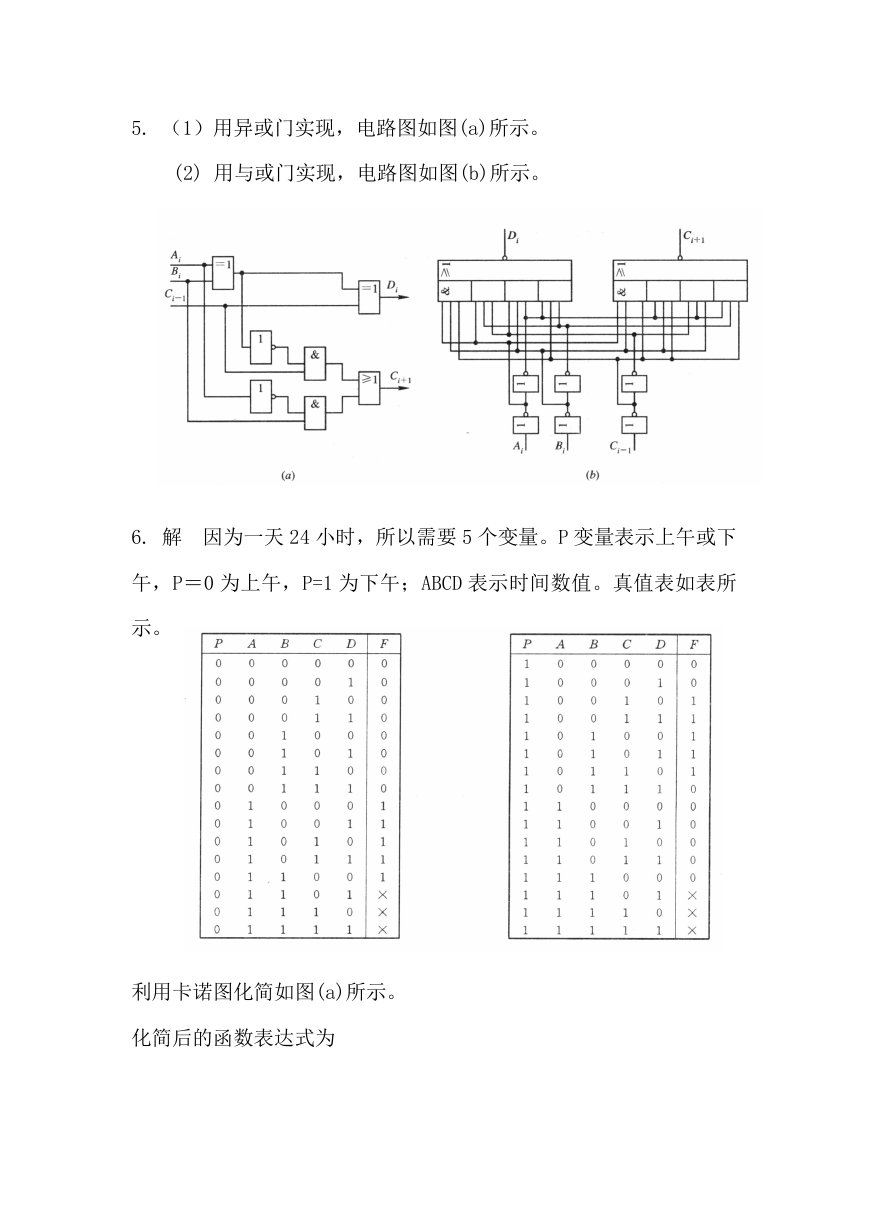
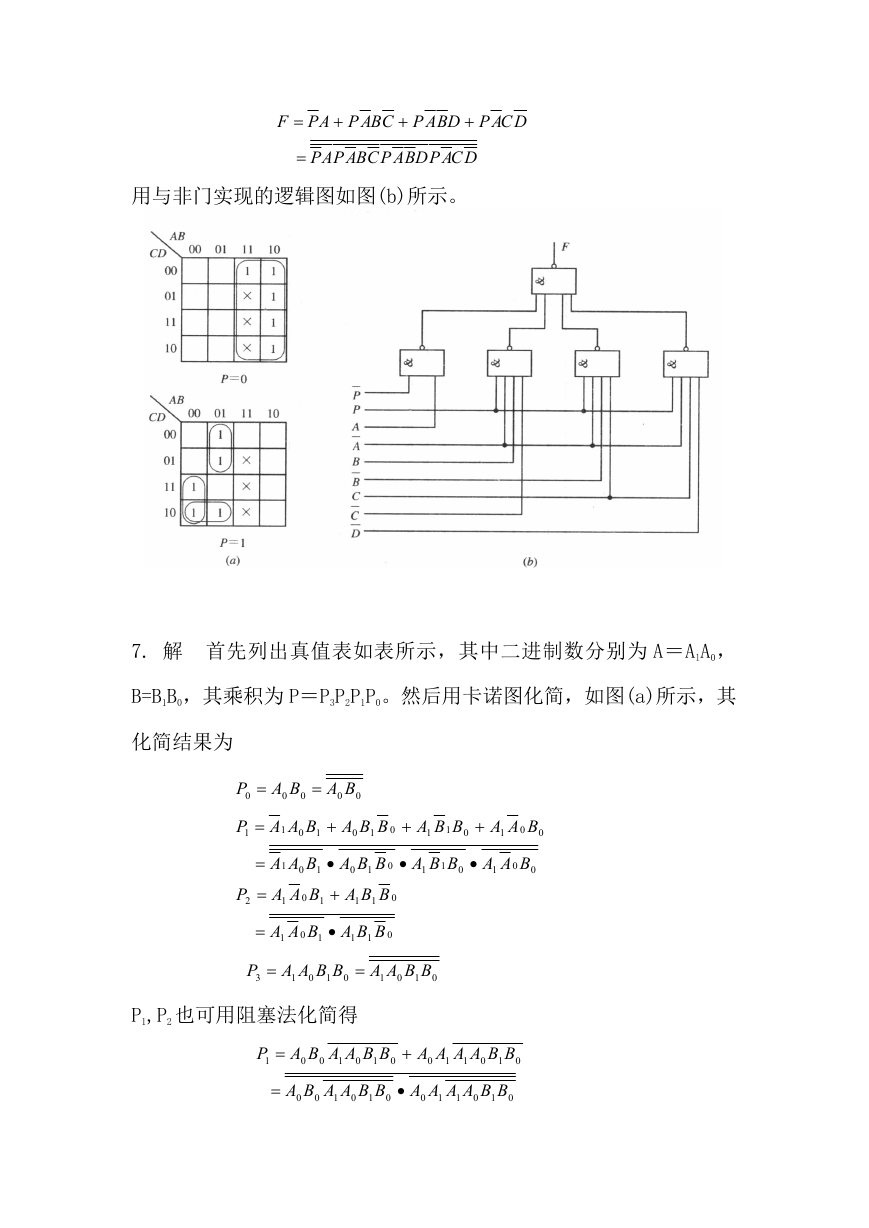
5. （1）用异或门实现，电路图如图(a)所示。 (2) 用与或门实现，电路图如图(b)所示。 6. 解因为一天 24 小时，所以需要 5 个变量。P 变量表示上午或下午，P＝0 为上午，P=1 为下午；ABCD 表示时间数值。真值表如表所示。利用卡诺图化简如图(a)所示。化简后的函数表达式为

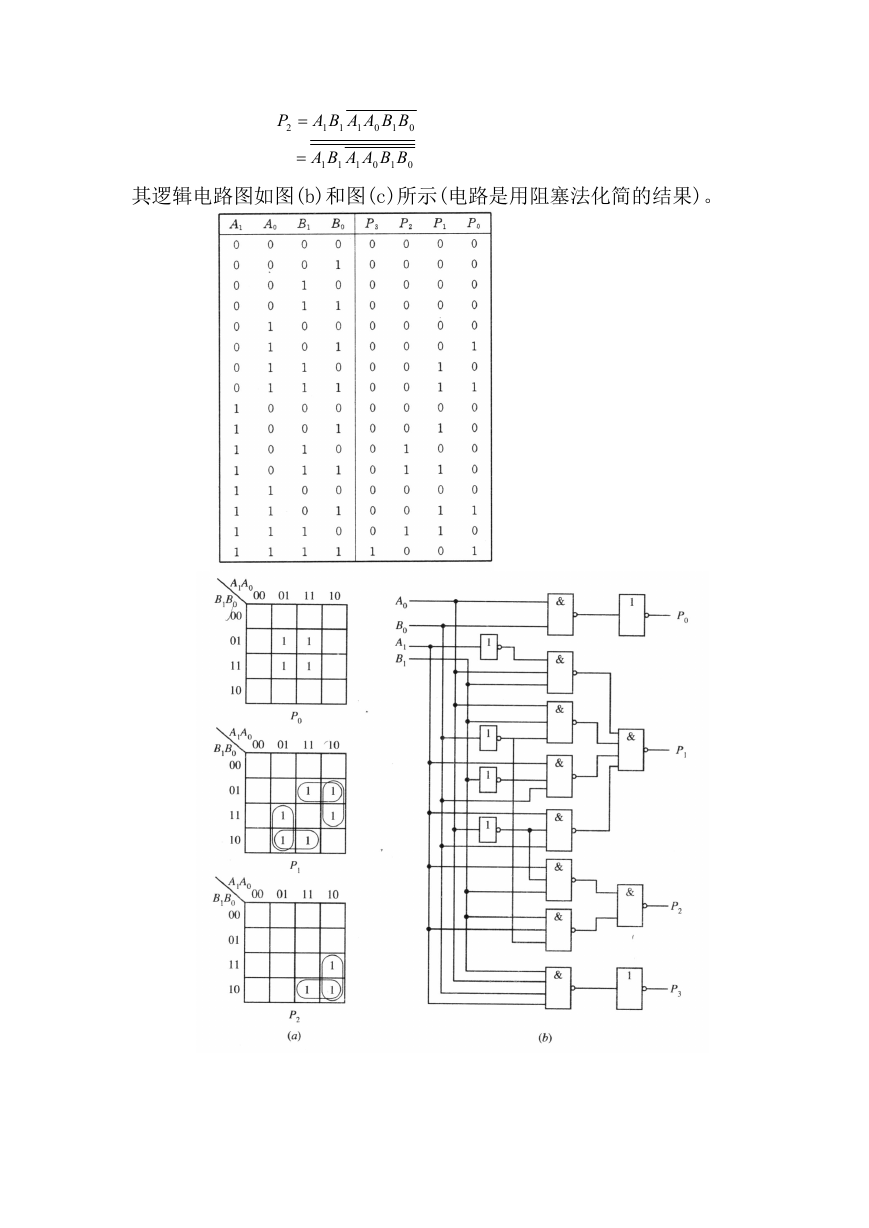
DCAPDBAPCBAPAPF      DCAPDBAPCBAPAP 用与非门实现的逻辑图如图(b)所示。 7. 解首先列出真值表如表所示，其中二进制数分别为 A＝AlA0， B=B1B0，其乘积为 P＝P3P2P1P0。然后用卡诺图化简，如图(a)所示，其化简结果为 P 0  BA 0 0  BA 0 0 P 1  BAA 1 1 0  BBA 0 1 0  BBA 1 1 0  BAA 1 0 0  BBA 1 1 0  BAA 1 0 0   P 2 0 BAA 1 1 BAA 1 1 0   1 BBA 0 0 BBA 1 1 0  BAA 1 1 0  BBA 1 1 0 P 3  BBAA 1 1 0  0 P1,P2 也可用阻塞法化简得 BBAA 1 1 0 0 P 1   BBAABA 0 1 0 1 0  0 BBAAAA 0 1 0 1 1 0 BBAABA 0 0 1 0 1  0 BBAAAA 0 1 0 1 1 0

P 2   BBAABA 1 1 1 1 0 0 BBAABA 1 0 1 1 1 0 其逻辑电路图如图(b)和图(c)所示(电路是用阻塞法化简的结果)。

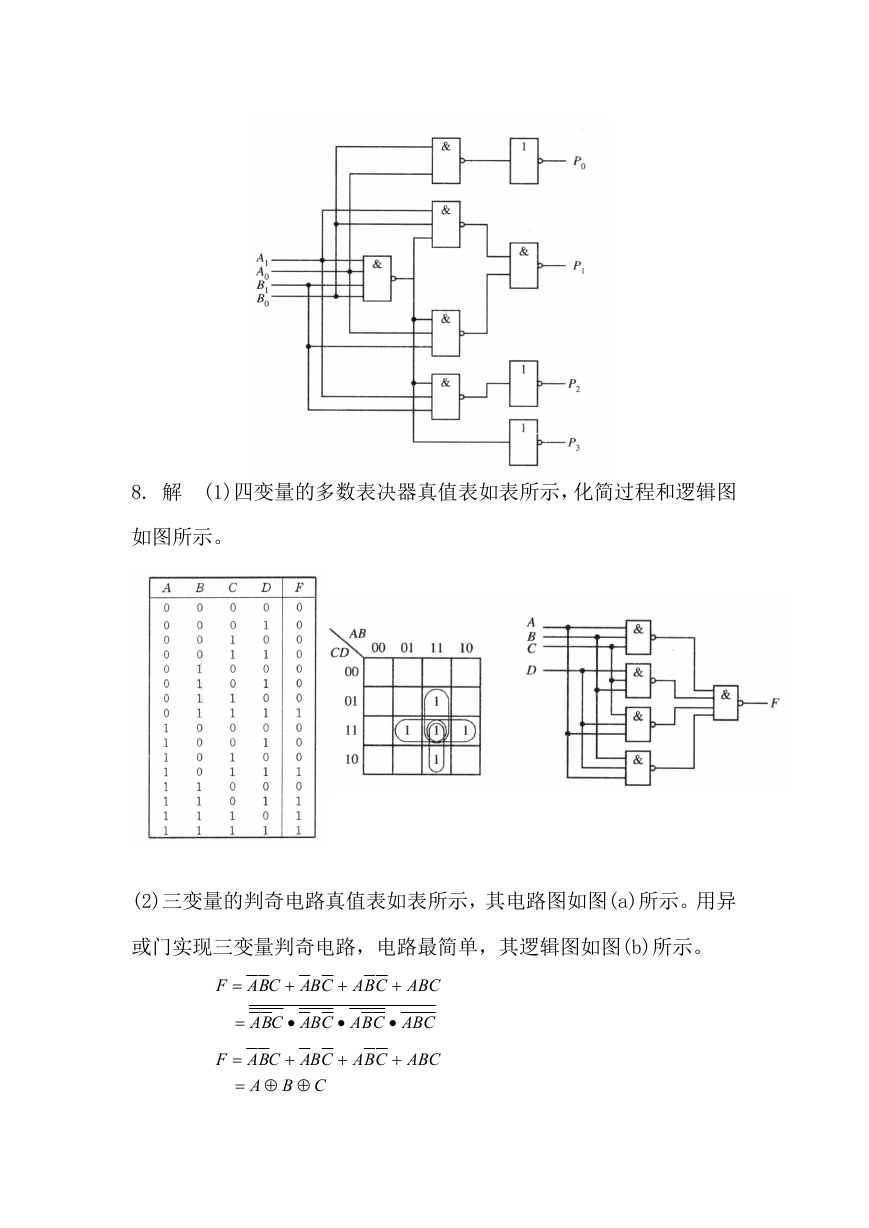
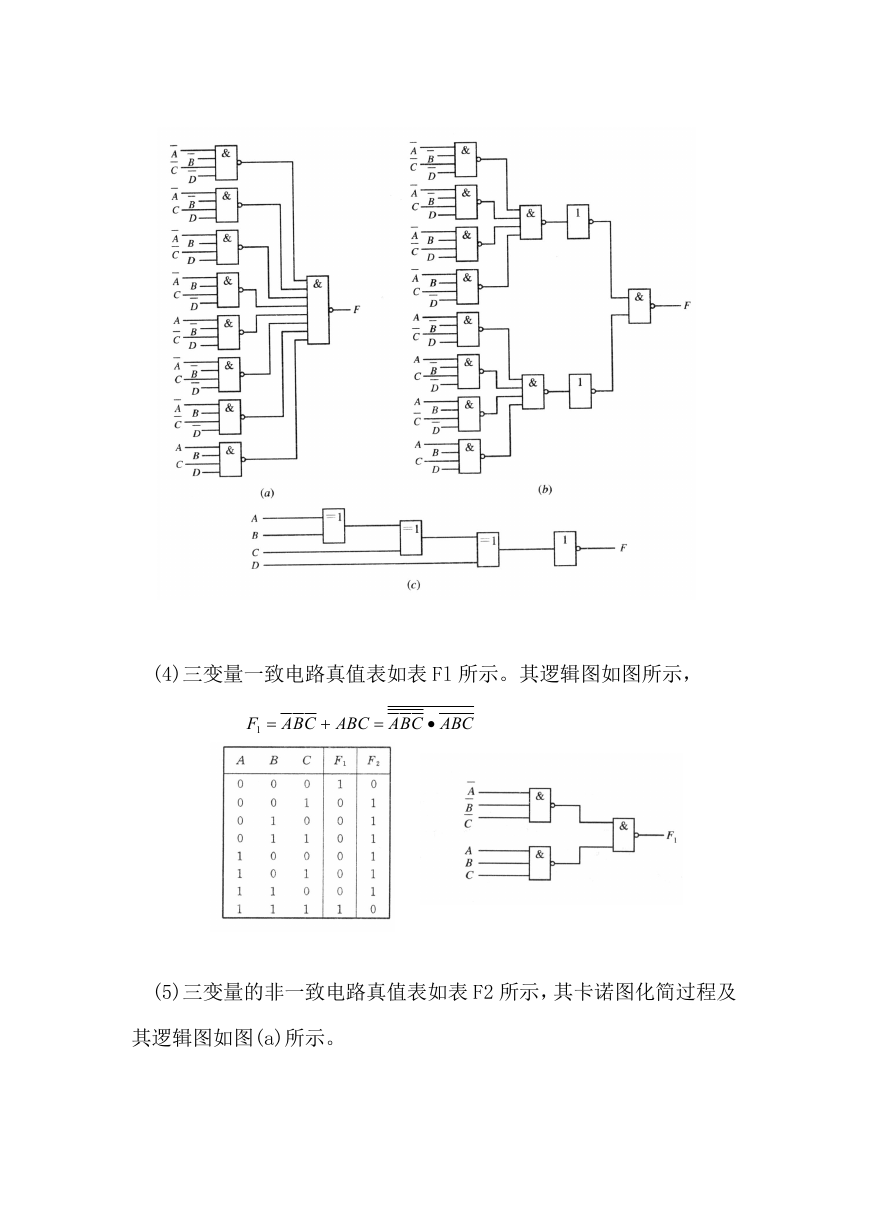
8. 解 (1)四变量的多数表决器真值表如表所示，化简过程和逻辑图如图所示。 (2)三变量的判奇电路真值表如表所示，其电路图如图(a)所示。用异或门实现三变量判奇电路，电路最简单，其逻辑图如图(b)所示。 CBACBACBAF     CBACBACBA   CBACBACBAF     CB A  ABC  ABC  ABC

(3)四变量的判偶电路真值表如表所示。 mF  3     m m m 10 0 mmmmmm m m        10 3 5 5 6 6 0 9 9  m 12 m  12  m 15 m 15  八个输入端的与非门价格较贵，其逻辑图如图(a)所示，如限定用四输入与非门实现，应按如下方法处理，电路如图(b)所示。 mF  0  m 3  m 5  mm 6 9  m 10  m 12  m 15  mmmmmm      3 0 9 6 5  m 12  m 15 10 最简单的电路是利用异或门实现，如图(c)所示。 AF  DCB

(4)三变量一致电路真值表如表 Fl 所示。其逻辑图如图所示， F 1 CBA  ABC  CBA  ABC (5)三变量的非一致电路真值表如表 F2 所示，其卡诺图化简过程及其逻辑图如图(a)所示。

分享到：

赞收藏

资料库

数字电子技术-第四章课后习题答案-(江晓安等编).doc

相关推荐

课程资源

热门标签

最新资料