logo资料库

分数傅里叶域多图像干涉加密技术.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.91M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 分数傅里叶域多图像干涉加密技术 秦海涛，钟志** （哈尔滨工程大学信息与通信工程学院，哈尔滨 150001） 摘要：提出一种新的多图像干涉加密方法，该方法分为 2 个步骤，首先通过离散余弦变换及 置乱将多幅图像融合成一幅实值图像，然后利用分数傅里叶域干涉加密算法，将其加密成 2 幅图像。置乱过程中的 2 个密钥非预先设定的数值，而是与原始图像有关，所以该方法可以 抵抗选择明文攻击；置乱过程的密钥空间极大，可以有效抵抗暴力攻击。该方法原理简单， 无需迭代操作。解密时，不需要使用全息技术获取相位信息，利用光强探测器、计算机等设 备即可获取解密图像，容易通过光学方法实现。通过计算机数值模拟仿真，对该算法的安全 性进行验证，并详细分析了密钥的敏感性，该方法计算量较小，实现简单，应用前景广阔。 关键词：多图像干涉加密；分数傅里叶域；离散余弦变换；混沌置乱 中图分类号：O438.2 Research on interference-based multiple-image encryption in the fraction Fouier domain Qin Haitao, Zhong Zhi (Information and Communication Engineering Institute, Harbin Engineering University, Haerbin 150001) Abstract: In this paper a novel interference-based multiple-image encryption system is proposed, which has two steps: firstly, the original images are combined into a real-valued signal by discrete cosine transform and scrambling technology, then the complex signal is encoded into two images by the interference-based encryption algorithm in the fractional Fourier domain. Two of the three keys in the scrambling process is relating to the original images and not pre-set, so this method is resistant to chosen-plaintext attacks. The key space in the scrambling process is so large that this method is resistant to brute force attack effectively. The encryption algorithm is quite simple and does not require iterative operation. And the decrypted process can be realized optically easily by light intensity detector without using holography to obtain the phase information. If one of the keys is wrong, the effective information of the original images cannot be got. Numerical simulation experiments have been carried out to verify the reliability security, reliability of the proposed methods and analysis the sensitivity of key. These algorithms have less computation, simplified operation and great prospects of application. Key words: Interference-based multiple-image encryption; Fractional Fourier domain; Discrete cosine transform; Chaotic scrambling 5 10 15 20 25 30 35 0 引言 近几十年，因特网和现代通信技术迅猛发展，在人们的工作和生活中无处不在，影响甚 远。网络给人们带来极大便捷的同时，也带来了信息安全隐患问题。数字图像，是一种应用 广泛的多媒体形式，在图像传输、私人电子相册存储等方面有较多应用。对于国防等特殊领 40 域，数字图像的保密性要求远超其它领域。如何安全地进行数字图像的传输，已经成为一个 急需解决的问题，受到人们的密切关注。对数字图像进行加密处理，已成为了最为常用、最 为基本的方法，是目前首选的解决方案，数字图像的加密技术具有不容忽视的研究意义和重 作者简介：秦海涛(1989-)，男，硕士，主要研究图像加密 通信联系人：钟志(1976-)，男，副教授，主要研究方向：光电检测、光电仪器、光电信号信息处理、通信 信号信息处理. E-mail: zhongzhi@hrbeu.edu.cn - 1 -
    中国科技论文在线 http://www.paper.edu.cn 要作用[1]。在图像信息安全领域，光学图像加密技术表现出了巨大的潜力。光学图像加密技 术可以并行处理二维数据，还具有相位、振幅、波长等更多的自由度，而且能够高速地进行 45 固有计算。与电子加密相比，具有更加复杂的环境，能更有效地抵抗攻击，使得光学图像加 密技术在图像加密中占据着不可替代的重要位置。 基于干涉原理的光学图像加密技术，是近几年才在图像加密领域流行起来的。Zhang 和 Wang 于 2008 年首次利用干涉原理实现光学图像干涉加密，加密过程非常简单，不需要迭 代算法，只需运用干涉原理，通过计算机计算即可将一幅原始图像加密成两块相位板[2]。随 50 后，Zhang 和 Wang 将该算法应用于双图像加密[3]。但只有入射光波长 λ 和相位板与输出面 之间距离 l 为密钥，密钥空间很小。Zhu 和 Wang 等做了大量实验，验证了在光学图像加密 领域使用干涉原理的可行性[4-5]，Qin 和 Gong 利用位置复用技术，将多幅原始图像加密到三 块相位板中，但解密图像存在串扰问题[6]。Wang 和 Guo 提出了改进算法，解决了图像间串 扰的问题，但是加密算法相对复杂，加密效率较低[7]。 55 为了扩大密钥空间、提高系统加密效率，本文提出基于离散余弦变换的分数傅里叶域多 图像干涉加密算法，并引入改进的置乱加密，有效增强了系统的安全性。 1 算法原理 1.1 分数傅里叶域单图像干涉加密算法 分数傅里叶域单图像干涉加密算法的加密过程非常简单，不需要迭代算法，只需要通过 60 计算机计算即可得到加密图像 M1 和 M2。解密原理图，如图 1 所示。将两块纯相位板 M1 和 M2，分别放到输入面相应的位置，并用两束特定波长的平行相干光垂直照射 M1 和 M2， 两束光经过透镜和半透镜后，在输出面产生干涉现象，然后只需要利用光强探测器，就可在 系统输出面上得到解密图像。 65 图 1 解密原理图 Fig. 1 Diagram of the decryption principle 以 Q(x, y)表示原始图像，其大小为 x×y，那么可以利用 Q(x, y)和一个大小相等的随机相 位构造一个新的图像 Q′(x, y)，其表达式为： (1) 70 式中，rand(m, n)表示大小为 m×n，取值在(0,1)内的随机距阵。 - 2 - '(,)(,)exp2(,)QxyQxyirandxy
    中国科技论文在线 http://www.paper.edu.cn 为书写方便，令 P[•]表示二维分数傅里叶变换 Fa1,a2[•]，P-1[•]表示其逆变换。由干涉原 理可知： 则 75 因为 M2 为纯相位板，那么 最后可以得到： 80 (2) (3) (4) (5) (6) (7) 1.2 分数傅里叶域多图像干涉加密算法 分数傅里叶域多图像干涉加密原理如图 2 所示。加密 4 幅图像，用 fk(x, y) (k=1, 2, 3, 4) 代表第 k 幅图像。首先对每一幅原始图像做离散余弦变换，然后利用低通滤波器将变换域中 85 的低频信息过滤出来，再融合得到一幅复合图像，最后将复合图像置乱得到 M(x, y)。利用 式(5)、(6)，即可得到加密图像。 图 2 多图像干涉加密算法原理图 Fig. 2 Diagram of the interference-based multiple-image encryption algorithm 90 使用 Logistic 映射对复合图像进行置乱，其表达式为 (8) 式中，k∊(0, 4]称为分支参数，xn∊(0, 1)，n={0,1,2,3……}。当 k∊(3.5699456, 4]时，Logistic 映射处于混沌状态，即初始值为 x0 时，在 Logistic 映射下，可以产生非周期、不收敛的序列， 此序列可用于图像像素的置乱[8]。 95 图 3 为 x0=0.44 时 Logistic 映射的倍周期分岔示意图。随着分支参数 k 的改变，系统从 倍周期分岔进入了混沌状态。每一次分岔，原来处于稳定的状态的周期轨道失去稳定，并产 生两个新的稳定周期轨道，如此往复，最后进入混沌状态，即所有的周期轨道失去稳定状态， 并有无穷多个不稳定的周期轨道。 - 3 - '(,)exp1exp2QxyiMiMPP1exp1exp2'(,)iMiMQxyP1exp2'(,)exp1iMQxyiMP21*111['(,)]exp(1)['(,)]exp(1)['(,)]exp(1)QxyiMQxyiMQxyiMPPP111arg[['(,)]]arccos[[['(,)]]/2]MQxyabsQxyPP12arg[['(,)]exp(1)]MQxyiMP1(1)nnnxkxx
    中国科技论文在线 http://www.paper.edu.cn 100 105 110 图 3 Logistic 映射示意图 Fig. 3 Diagram of the Logistic mapping 利用 Logistic 映射，生成混沌序列，截取所需长度，并将序列元素按从小到大重新排列， 以序列元素位置变化的方式，改变原图像素的位置，便得到置乱图像。Logistic 映射中分支 参数 k，初始值 x0，截取位置参数 p 均为密钥，很大程度上扩大了密钥空间。若图像较大， 像素个数较多时，对每一个像素进行置乱，运算量会很大，消耗的时间也很长。为提高效率， 可以将待加密图像进行分块处理，再依照上述置乱方法进行置乱。但像素块不能过大，否则 达不到置乱的效果。 与传统给定初始值 x0，截取位置参数 p 的方式不同，此加密算法的这两个参数与 4 幅原 始图像有关，这样可以抵抗选择明文攻击[9]。参数 x0 与 p 的计算公式如下： (9) (10) 式中，sum 表示 4 幅原始图像所有像素值的和。 图 4 为分数傅里叶域多图像干涉加密算法的解密原理图。得到 M(x, y)的方法与得到 Q(x, y)的方法相同，然后对 M(x, y)进行解置乱操作，并过滤出每一幅图像的相应信息，做离散余 115 弦逆变换，即可得到解密图像。 图 4 多图像干涉加密算法解密原理图 Fig. 4 Diagram of the interference-based multiple-image decryption algorithm 2 仿真与分析 120 为了验证该算法的性能，使用 Matlab R2014a 进行了数值模拟仿真。 为了能更准确更客观地评价恢复图像的质量，引入归一化均方误差(Normalized Mean Square Error，NMSE)。恢复图像与原始图像之间的归一化均方误差的表达式为： - 4 - 0mod,1000/1000xsum3000mod,1000psum
    中国科技论文在线 http://www.paper.edu.cn (11) 式中，M×N 表示图像的大小，ID(x, y)表示解密图像在像素位置(x, y)处的灰度值，IO(x, y)表 示原始图像在像素位置(x, y)处的灰度值。归一化均方误差值越小，表示恢复图像与原始图像 125 130 的差异越小，系统的可靠性越好；反之，差异越大，系统可靠性差。 图 5(a)-(d)为原始图像，其大小均为以 4 幅 256×256 像素的灰度图作为原始图像。令置 乱过程的分支参数 k=3.95，经计算此次加密置乱过程的 x0=0.617，截取位置参数 p=3617。 原始图像经离散余弦变换、过滤、融合、置乱，得到 M(x, y)，其包含了 4 幅原始图像的大 部分信息，如图 5(e)所示。分数傅里叶变换的阶数为(a1,a2)=(0.35,0.35)，M(x, y)经过分数傅 里叶域干涉加密算法加密后，得到杂乱无章的加密图像 M1 和 M2，如图 5(f)和(g)所示，视 觉上无法从加密图像 M1 和 M2 中得到原始图像的任何有效信息。使用正确的密钥进行解密， 即可恢复出正确的复合频谱图 M(x, y)，如图 5(h)所示，恢复出来的 M(x, y)与原始 M(x, y)之 间的归一化均方误差值为 2.9604e-30，证明分数傅里叶域干涉加密算法的加密与解密过程中 135 几乎不存在误差。对恢复出的 M(x, y)做相应的分割，得到每一幅图像对应的变换域频谱， 最后做离散余弦逆变换，即可得到恢复图像。如图 5(i)-(l)所示。与原图进行对比，可看出解 密图像与原始图像几乎相同，没有串扰或失真，恢复图与原图的归一化均方误差值介于 0.0026 与 0.0062 之间，可见此算法具有很好的加密及解密效果，能很好地恢复出原始图像。 140 (a)原图 1 (b)原图 2 (c)原图 3 (d)原图 4 (e)M(x, y) (f)M1 (g)M2 (h)解密 M(x, y) (i)解密图 1 (j)解密图 2 (k)解密图 3 (l)解密图 4 145 图 5 加密及解密图像 Fig. 5 Encrypted and decrypted images 下面定量分析解密密钥与正确密钥存在偏差对解密图像质量的影响。4 幅图像的情况几 乎一致，因此仅对第一幅图像进行分析。当密钥(a1, a2)=(0.36, 0.36)，其他密钥均正确时，解 - 5 - 221111(,)(,)(,)NMNMDOOyxyxNMSEIxyIxyIxy
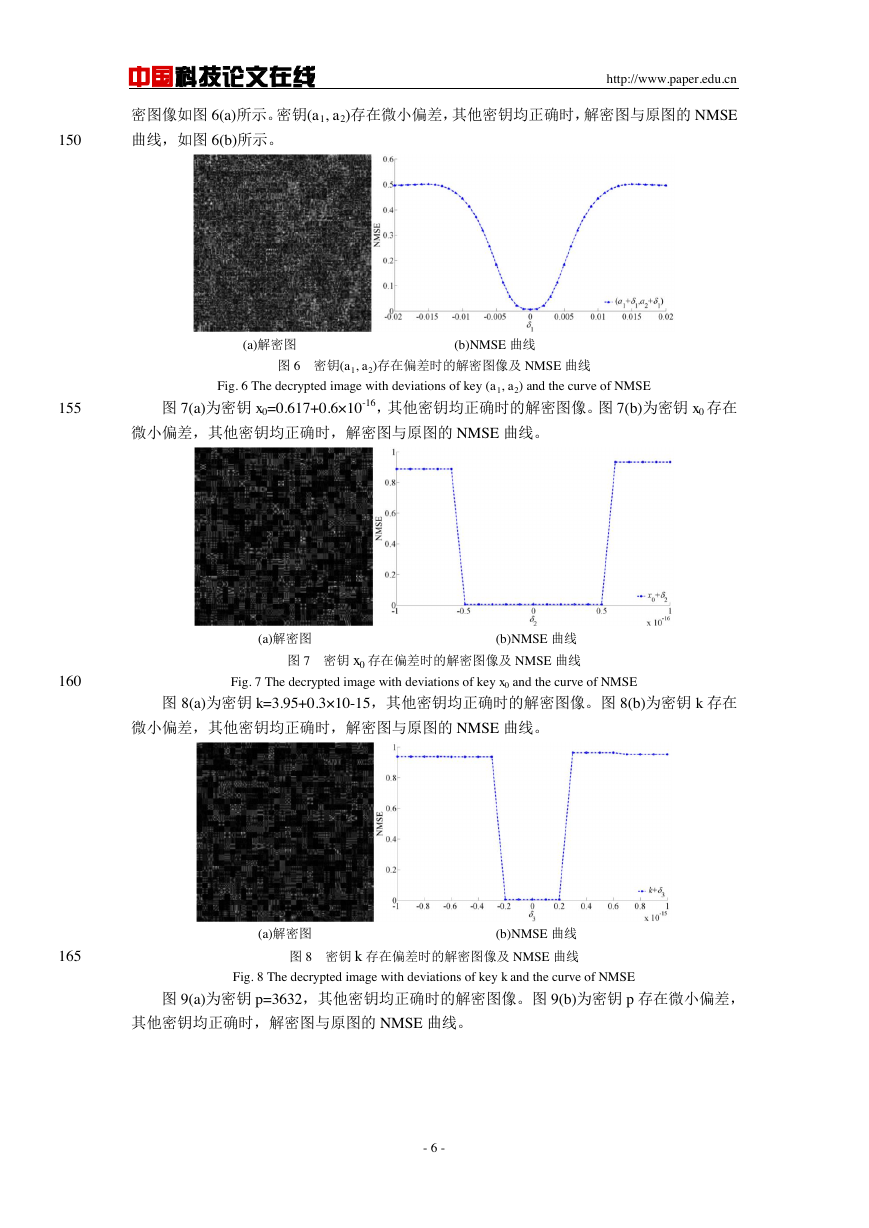
    中国科技论文在线 http://www.paper.edu.cn 密图像如图 6(a)所示。密钥(a1, a2)存在微小偏差，其他密钥均正确时，解密图与原图的 NMSE 曲线，如图 6(b)所示。 150 (a)解密图 (b)NMSE 曲线 图 6 密钥(a1, a2)存在偏差时的解密图像及 NMSE 曲线 Fig. 6 The decrypted image with deviations of key (a1, a2) and the curve of NMSE 155 图 7(a)为密钥 x0=0.617+0.6×10-16，其他密钥均正确时的解密图像。图 7(b)为密钥 x0 存在 微小偏差，其他密钥均正确时，解密图与原图的 NMSE 曲线。 (a)解密图 (b)NMSE 曲线 图 7 密钥 x0 存在偏差时的解密图像及 NMSE 曲线 160 Fig. 7 The decrypted image with deviations of key x0 and the curve of NMSE 图 8(a)为密钥 k=3.95+0.3×10-15，其他密钥均正确时的解密图像。图 8(b)为密钥 k 存在 微小偏差，其他密钥均正确时，解密图与原图的 NMSE 曲线。 (a)解密图 (b)NMSE 曲线 165 图 8 密钥 k 存在偏差时的解密图像及 NMSE 曲线 Fig. 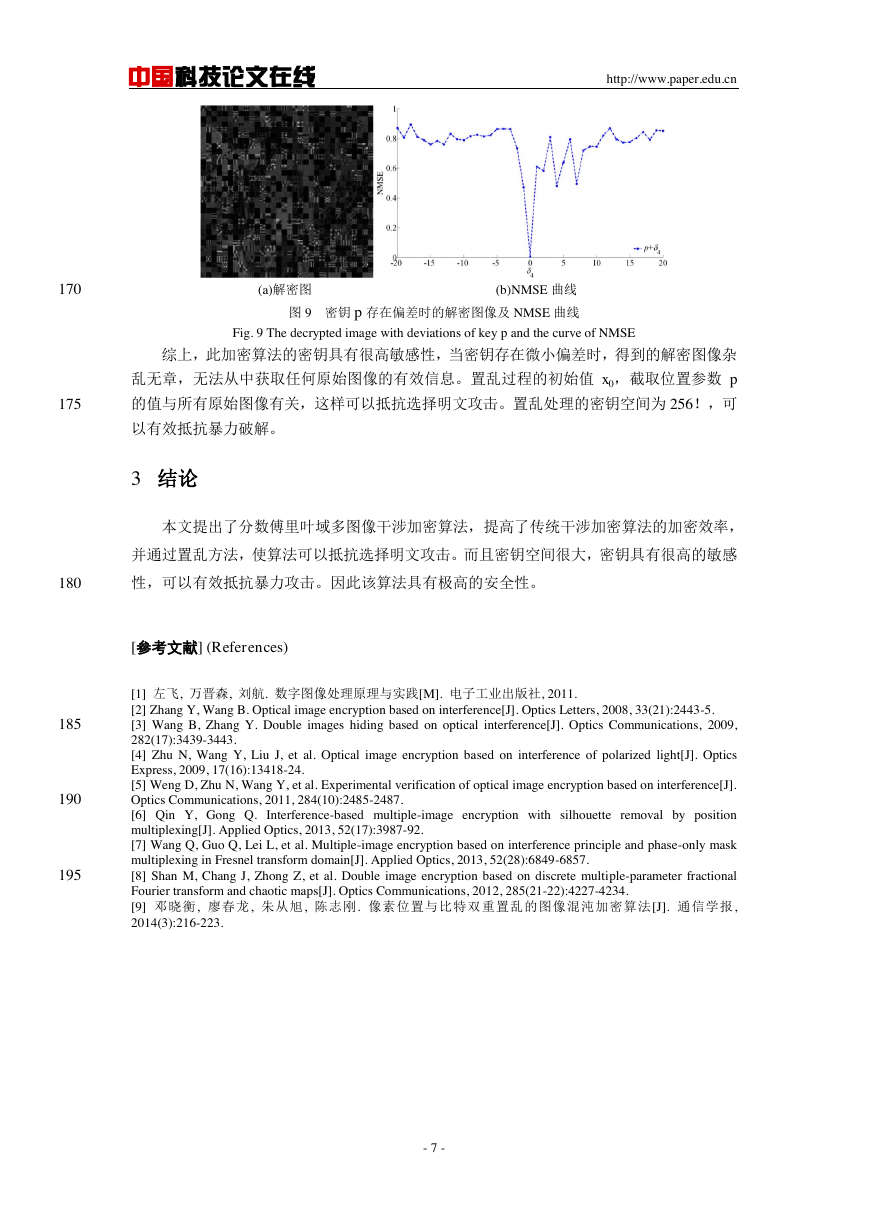8 The decrypted image with deviations of key k and the curve of NMSE 图 9(a)为密钥 p=3632，其他密钥均正确时的解密图像。图 9(b)为密钥 p 存在微小偏差， 其他密钥均正确时，解密图与原图的 NMSE 曲线。 - 6 -
    中国科技论文在线 http://www.paper.edu.cn 170 (a)解密图 (b)NMSE 曲线 图 9 密钥 p 存在偏差时的解密图像及 NMSE 曲线 Fig. 9 The decrypted image with deviations of key p and the curve of NMSE 综上，此加密算法的密钥具有很高敏感性，当密钥存在微小偏差时，得到的解密图像杂 乱无章，无法从中获取任何原始图像的有效信息。置乱过程的初始值 x0，截取位置参数 p 的值与所有原始图像有关，这样可以抵抗选择明文攻击。置乱处理的密钥空间为 256！，可 175 以有效抵抗暴力破解。 3 结论 本文提出了分数傅里叶域多图像干涉加密算法，提高了传统干涉加密算法的加密效率， 并通过置乱方法，使算法可以抵抗选择明文攻击。而且密钥空间很大，密钥具有很高的敏感 180 性，可以有效抵抗暴力攻击。因此该算法具有极高的安全性。 [参考文献] (References) 185 190 195 [1] 左飞, 万晋森, 刘航. 数字图像处理原理与实践[M]. 电子工业出版社, 2011. [2] Zhang Y, Wang B. Optical image encryption based on interference[J]. Optics Letters, 2008, 33(21):2443-5. [3] Wang B, Zhang Y. Double images hiding based on optical interference[J]. Optics Communications, 2009, 282(17):3439-3443. [4] Zhu N, Wang Y, Liu J, et al. Optical image encryption based on interference of polarized light[J]. Optics Express, 2009, 17(16):13418-24. [5] Weng D, Zhu N, Wang Y, et al. Experimental verification of optical image encryption based on interference[J]. Optics Communications, 2011, 284(10):2485-2487. [6] Qin Y, Gong Q. Interference-based multiple-image encryption with silhouette removal by position multiplexing[J]. Applied Optics, 2013, 52(17):3987-92. [7] Wang Q, Guo Q, Lei L, et al. Multiple-image encryption based on interference principle and phase-only mask multiplexing in Fresnel transform domain[J]. Applied Optics, 2013, 52(28):6849-6857. [8] Shan M, Chang J, Zhong Z, et al. Double image encryption based on discrete multiple-parameter fractional Fourier transform and chaotic maps[J]. Optics Communications, 2012, 285(21-22):4227-4234. [9] 邓晓衡, 廖春龙, 朱从旭, 陈志刚. 像素位置与比特双重置乱的图像混沌加密算法[J]. 通信学报, 2014(3):216-223. - 7 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料