1254 978-1-4577-1348-4/11/$26.00 ©2011 IEEE 2011 IEEE 22nd International Symposium on Personal, Indoor and Mobile Radio Communications Usability of Apple iPhones for Inertial Navigation Systems corina.schindhelm@siemens.com florian.gschwandtner@ifi.lmu.de CT T DE IT 1 Siemens AG Department for Informatics Corina Kim Schindhelm Florian Gschwandtner I. INTRODUCTION University of Munich Munich, Germany Munich, Germany For that reason, inertial systems are used for indoor posi- tioning. Knowing an initial position, all subsequent positions can be calculated using various sensor data, which do not require any infrastructure and ensure the user’s privacy. A lot of research was done in the area of inertial positioning systems using expensive and distinct devices. However, since modern devices are often equipped with inertial sensors, they could be used for common inertial positioning systems. Hence, we decided to examine two common devices, the Apple iPhone 3GS and the iPhone 4, on their capability of being used for inertial positioning using standard algorithms. The remainder is structured as followed: Sec. II introduces inertial navigation and list some reference work. Sec. III describes the devices, the algorithms and filters applied. Sec. IV introduces preliminarily results and Sec. V concludes the paper with future work. II. INERTIAL NAVIGATION SYSTEMS Inertial Navigation is an autonomous navigation aid. Based on an initial position, orientation (direction), and velocity (speed), an INS continuously calculates consecutive positions of a moving target. Thus, an INS consists of an entity equipped with sensors, typically an inertial measure- ment unit (IMU), which measures the data and an algorithm, which processes the data and calculates positions. The IMU is responsible for measuring acceleration and rotation. To obtain initial orientation of a full six-degree of freedom IMU, at least six sensors, three for the rotation (pitch, roll, yaw) and three for the acceleration (x, y, z) in every direction are needed. The algorithm that processes the IMU data is called dead reckoning. Based on an initial position, the current position is calculated with the aid of the current direction of motion, the velocity or the distance traveled. Besides the initial position, this system is completely independent from outside data sources, and thus allows for a privacy friendly self positioning. However, drawbacks like drifts and incorrect positions can result from small sensor measurement deviations. Woodman [3] describes the principle of inertial navigation and creates a simulator where sensor data can be observed Michael Banholzer Department for Informatics University of Munich Munich, Germany banholzer@cip.ifi.lmu.de Abstract—In recent decades, many indoor positioning tech- niques have been researched and some approaches have even been developed into consumer products. Most of them have been deployed into companies which benefit from indoor asset tracking. However, for public buildings like libraries or transportation systems, no direct benefit exists by installing expensive systems. Inertial navigation systems offer a form of positioning which is almost completely independent from external infrastructures, inexpensive and privacy friendly. As prices for sensors continuously drop, mobile terminals, such as cell phones or tablet PCs, are being equipped with various additional components, like GPS, cameras and light sensors, and moreover gyroscopes, compasses and accelerometers in- tegration is also becoming commonplace. These last three components enable inertial navigation systems to calculate the position of the device. In this paper, we selected two devices, the iPhone 3GS and the iPhone 4, to analyze their sensors for usability of an inertial navigation system. For each device a common strapdown algorithm was implemented and varying standard filters applied to clean the output data stream of the sensors. Finally, we present the results, which are diverse according to the devices. Keywords-Inertial Navigation System, INS, Apple iPhone Indoor positioning techniques are not hypothetical re- search theories anymore but have been deployed into compa- nies with sufficient funds to invest in expensive high preci- sion technologies like Ultra Wide Band . Conversely, public buildings have no monetary incentive and must find low cost solutions. Some institutions use existing hardware and add software to achieve an additional advantage for visitors, like in the New York Museum of Natural History [1], which allows user to find their own position and corresponding exhibit information on a map via WiFi positioning. Independent of the underlying technology, K”upper [2] outlines four different positioning topologies based on which component measures signals and/or calculates the position: Network based, terminal assisted, terminal based and net- work assisted. All these solutions depend to a greater or lesser extent on the infrastructure controlled by a third party which can affect the user’s privacy. Therefore, it is important to reduce the dependency on a foreign infrastructure and to make it impossible for a third party to detect or localize the user. 

1255 (6) By integrating |ag|, the velocity vg(t) and the displace- ment sp(t) are obtained. vg(t) = vg(0) + |ag|(t)dt a =α x α y α ag = a A(φ θ ψ) z T t t−δt t sp(t) = vg(t)dt t−δt (5) (7) (8) The vector vg(0) represents the past velocity. To obtain the current velocity at time t the previous velocity has to be added to the integral of the vector ag. The vector for the correct direction is calculated by normalizing and scaling vg Figure 2: iPhone 4 strapdown algorithm along the direction of movement. As a result, the calculation of velocity and path are specified by i+δt i+δt i t t i=0 i=0 i v(t) = s(t) = a(t)dt, t ∈ R, v(t)dt, t ∈ R. (1) (2) where δt is the sample duration. The direction of a single moved fraction is gathered from the compass αc and the rotation matrix R, given by cos α −sinα t cos α sin α R(α) = p(t) = s(0) + R(αc) t−δt , (3) (4) v(t)dt, The user’s acceleration is defined by the vectors α where s(0) is the passed path and δt the sample duration. However, with the iPhone 4, the Apple Inc. framework exposes the orientation (pitch, roll, yaw) of the device and subtracts gravity as well. Figure 2 illustrates the algorithm. x, α y and α z. To transform the values into the global coordinate system, a vector a is formed by these values and transformed with the orientation of the device by Euler’s rotation matrix A (see [13]). The resulting vector is given in Equation 6. Figure 1: iPhone 3GS Strapdown algorithm and various error sources modeled to examine increasing inaccuracy over time. He also shows that sensor fusion can help reducing drifts caused by inaccurate gyroscopes. Jorge Lobo et al. [4] focus on the hardware realization of an INS for mobile land vehicles like cars. They analyze the sensor characteristics and investigate magnetic shields for compasses. Land vehicles are also considered in [5], presenting an algorithm for initial calibration and alignment especially designed for low cost IMUs. There are different approaches for indoor localization using inertial sensors. In [6] and [7], the authors utilize a wearable electromagnetic tracker to retrieve the geometrical relationship between the user’s heel and waist, and a com- pass sensor for the user’s orientation. In [8], inertial sensors are used in shoes to function as pedometers, whereas other approaches like [9] and [10] utilizes accelerometers and gyroscopes to retrieve the walked distance and a compass sensor for direction. Woodman et al. [11] employ a foot-mounted IMU to realize an indoor local- ization system supporting multiple floors and stairways. III. INERTIAL NAVIGATION ON DEVICES This section offers an overview of the hardware embedded in the devices, the strapdown algorithms and the filters. A. Devices The Apple iPhone 3GS is equipped with a three axis accelerometer from STMicroelectronics (LIS331DL) and a compass from AKM Semiconductor Inc. (AK8973) [12]. The maximum update frequency of the accelerometer is approximately 100 Hz. In addition to the accelerometer (LIS331DLH) and compass (AK8975), the iPhone 4 offers a three axis gyroscope L3G4200D [12]. B. Strapdown algorithms Based on the work of Woodman [3], we implemented a strapdown system for each device. Strapdown systems calculate the orientation and the speed of the device and combine them to compute the direction of motion. Figure 1 shows the concept of the algorithm for the iPhone 3GS. Since the iPhone 3GS doesn’t contain gyroscopes, the orientation of the device cannot be calculated making it impossible to subtract gravity from the accelerometer data. To overcome this problem, we assume the device to be perpendicular to gravity. The combination of only a one-dimensional accelerometer and a compass makes it necessary to mount the device with the y-accelerometer ∫∫Compass dataAccelerometer dataVelocityPositionInitialPositionWayProjectaccelerationonto globalaxes∫∫VelocityGlobalAcceleration∫Subtractearth gravitythroughorientationGyroscope dataOrientationAccelerometer dataPosition

1256 Figure 3: Filters for the iPhone 3GS strapdown algorithm with the length of the displacement sp(t) and finally added to the passed path: sf raction(t) = vg|vg| sp(t), sg(t) = sg(0) + sf raction(t) (9) (10) where the path passed is sg(0) and the new calculated path is denoted by sf raction(t). C. Filters An initial calibration is needed to calculate the standard deviation of a stationary device. This can be conducted, e.g. by leaving the device unmoved while observing occuring deviations. Subsequently, the mean deviation can be used to correct the signals. Threshold filters trigger only when a certain predetermined value is exceeded, which results in a real zero value for motionless devices. f (α) = if |α| ≥ t, otherwise, where t ∈ R. α, 0, (11) High pass filters allow signals to pass above its cut-off frequency and attenuate or filter out those that fall below it. The filter is defined at time t by the function η(t) = 1 r 1 r + 1 f (η(t − 1) + αy(t) − αy(t − 1)) , (12) where αy(t) is the y-accelerometer value at time t, r is the sample rate and f the cutoff frequency [14]. Based on its highest update frequency, the iPhone 3GS has a sample rate of 100Hz. The main principle of a Kalman filter is to predict the new state, its uncertainty and further to correct the predictions with the new measurements. The filter is based on the following equations [15]: xk = Axk−1 + Buk + wk−1 zk = Hxk + vk (13) The signal value xk is built upon its previous value plus a control signal and a process noise. zk is formed by a linear combination of the signal value and the measurement noise. Normally, A, B and H are matrices. A defines the state transition between two timesteps k − 1 and k. The control input matrix B wasn’t used because our model contains no control signals yet. The matrix H is the observation model Figure 4: Filters for the iPhone 4 strapdown algorithm which maps the observed vector into the current estimated state vector. The vector v specifies the measurement noise (e.g. noise of the accelerometer). The vector w holds the process noise which has to be adjusted for every redefined model or scenario. This value contributes to the overall uncertainty of the model. We used a one-dimensional Kalman filter, where the state matrices have been removed [16]: xk = xk−1 + Kk(zk − xk−1), Pk = (1 − Kk−1)Pk−1 + w, Kk = Pk Pk + R , (14) (15) (16) where the process noise is given by the constant w and stands for the overall uncertainty of the entire error rate. The measurement noise R defines the inaccuracy of the sensor. The value zk at the instant k is the measured value of the sensor and Kk is the Kalman gain. It is the most significant value which will be found due to the algorithm, but controlled by the estimates of noise w and R. A disadvantage of the Kalman filter is the time shift of the filtered values. The duration of the shift depends on the defined parameters for the filter. The algorithms from the previous section must be en- hanced by filtering to consider inaccuracy and noise. For the iPhone 3GS, three filter techniques are applied before the actual calculation starts (Figure 3). The calibration filter C is supposed to eliminate big variations and the threshold filter T makes a smooth zero stationary signal. A final filter H/K (high-pass or Kalman filter) is chosen based on the scenario. For the iPhone 4, only the last two filter techniques are applied (Figure 4). The API for the iPhone 4 makes the calibration filter unnecessary, since it already calibrates the user acceleration data. IV. TEST RESULTS To enable the deployement on mobile devices, we fo- cused on an efficient implementation in regards to limited resources. We also developed a logging application to record and process the results and visualize them on the computer in 3D. In the following, the different conducted experiments are described and the results depicted. ∫∫Compass dataAccelerometer dataVelocityPositionInitialPositionWayCTH/KProjectaccelerationonto globalaxes∫∫VelocityGlobalAcceleration∫Subtractearth gravitythroughorientationGyroscope dataOrientationAccelerometer dataPositionTH/K

1257 iPhone 3GS is not an ideal choice for inertial navigation. It is very sensitive to its environment and has the effect of being misleading. Metallic objects or electronic devices positioned close to the compass have such a high influence on the course that the data becomes useless. Additionally, when turning and moving the device, the compass needs a lot of time to determine the new course. Another source of error arises when the device is not kept precisely horizontal causing gravity to influence the acceler- ation data. As a result, the algorithm calculates velocity and position with incorrect acceleration values. B. Apple iPhone 4 sensors For testing the IPhone 4, our scenario was simply a walked circle with radius of one meter with the smartphone held in the hand. Different combinations of threshold filter and Kalman filter with various parameters were examined. 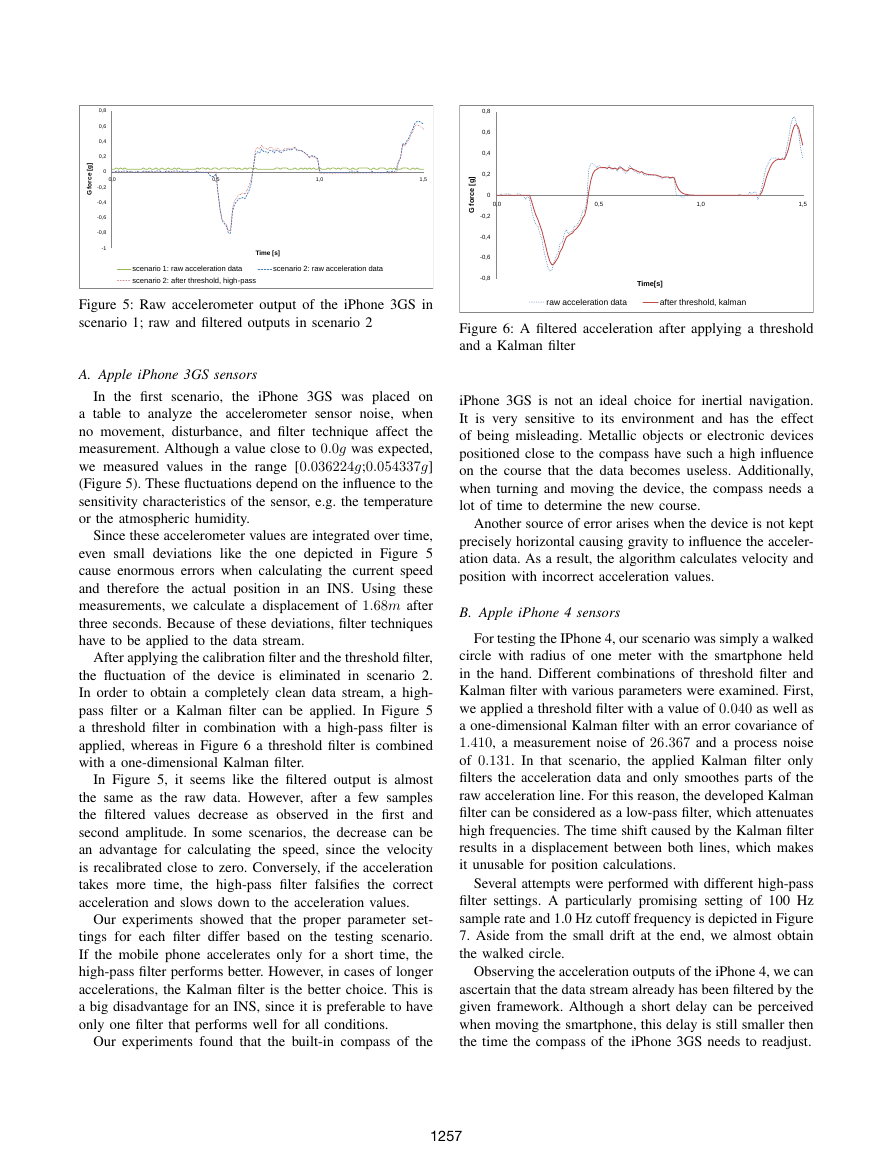First, we applied a threshold filter with a value of 0.040 as well as a one-dimensional Kalman filter with an error covariance of 1.410, a measurement noise of 26.367 and a process noise of 0.131. In that scenario, the applied Kalman filter only filters the acceleration data and only smoothes parts of the raw acceleration line. For this reason, the developed Kalman filter can be considered as a low-pass filter, which attenuates high frequencies. The time shift caused by the Kalman filter results in a displacement between both lines, which makes it unusable for position calculations. Several attempts were performed with different high-pass filter settings. A particularly promising setting of 100 Hz sample rate and 1.0 Hz cutoff frequency is depicted in Figure 7. Aside from the small drift at the end, we almost obtain the walked circle. Observing the acceleration outputs of the iPhone 4, we can ascertain that the data stream already has been filtered by the given framework. Although a short delay can be perceived when moving the smartphone, this delay is still smaller then the time the compass of the iPhone 3GS needs to readjust. Figure 6: A filtered acceleration after applying a threshold and a Kalman filter Figure 5: Raw accelerometer output of the iPhone 3GS in scenario 1; raw and filtered outputs in scenario 2 A. Apple iPhone 3GS sensors In the first scenario, the iPhone 3GS was placed on a table to analyze the accelerometer sensor noise, when no movement, disturbance, and filter technique affect the measurement. Although a value close to 0.0g was expected, we measured values in the range [0.036224g;0.054337g] (Figure 5). These fluctuations depend on the influence to the sensitivity characteristics of the sensor, e.g. the temperature or the atmospheric humidity. Since these accelerometer values are integrated over time, even small deviations like the one depicted in Figure 5 cause enormous errors when calculating the current speed and therefore the actual position in an INS. Using these measurements, we calculate a displacement of 1.68m after three seconds. Because of these deviations, filter techniques have to be applied to the data stream. After applying the calibration filter and the threshold filter, the fluctuation of the device is eliminated in scenario 2. In order to obtain a completely clean data stream, a high- pass filter or a Kalman filter can be applied. In Figure 5 a threshold filter in combination with a high-pass filter is applied, whereas in Figure 6 a threshold filter is combined with a one-dimensional Kalman filter. In Figure 5, it seems like the filtered output is almost the same as the raw data. However, after a few samples the filtered values decrease as observed in the first and second amplitude. In some scenarios, the decrease can be an advantage for calculating the speed, since the velocity is recalibrated close to zero. Conversely, if the acceleration takes more time, the high-pass filter falsifies the correct acceleration and slows down to the acceleration values. Our experiments showed that the proper parameter set- tings for each filter differ based on the testing scenario. If the mobile phone accelerates only for a short time, the high-pass filter performs better. However, in cases of longer accelerations, the Kalman filter is the better choice. This is a big disadvantage for an INS, since it is preferable to have only one filter that performs well for all conditions. Our experiments found that the built-in compass of the -1-0,8-0,6-0,4-0,200,20,40,60,80,00,51,01,5Gforce[g]Time[s]scenario1:rawaccelerationdatascenario2:rawaccelerationdatascenario2:afterthreshold,high-pass-0,8-0,6-0,4-0,200,20,40,60,80,00,51,01,5Gforce[g]Time[s]rawaccelerationdataafterthreshold,kalman

1258 By examining the raw accelerometer data of the iPhone 3GS and iPhone 4, it becomes clear that low-cost MEMS are used in both. These MEMSs offer sufficient results when recorded for a short time. However, if a calculation takes longer and depends on previous calculations, the results be- come inaccurate and useless. Fluctuation and jitter contribute to the inaccuracy and make an exact determination of the velocity and the position difficult. Due to the necessity of filtering the data stream, further losses of information arise and increase over time. V. CONLUSION In this paper two common devices were examined on their ability to support an inertial navigation system. For each device, a strapdown algorithm was implemented. Since both iPhones use cheap, inaccurate, and noisy sensors, a strapdown algorithm cannot fully realize a precise INS. As a result, various filters were applied to increase the accuracy. Finally, tests were carried out to analyze and verify the strapdown algorithms and to find the best combination of filters for each device. However, the tests show that even with the use of filters it is challenging to build a precise INS using sensors from common devices because of their inaccuracies and high error rate. The results show that the iPhone 4 can provide tolerable results for a short time, but then the deviation becomes too high because of the error rate. Currently we are implementing a multi-dimensional Kalman filter to examine possible enhancements. Furthermore we try to improve the system by using more sensors from the iPhone 4, e.g. light sensors and camera. REFERENCES [1] L. Perry-Lube and M. Lefkowitz, “Explorer - mobile navi- gation and interpretation at the american museum of natural history,” in Museums and the Web 2011, Trant and Bearman, Eds., 2011. Figure 7: A walked circle with the iPhone 4 when applying a threshold filter and a high-pass filter [2] A. K¨upper, Location-Based Services: Fundamentals and Op- eration. Wiley, October 2005. [3] O. J. Woodman, “An introduction to inertial navigation,” University of Cambridge, Computer Laboratory, Tech. Rep. UCAM-CL-TR-696, Aug. 2007. [4] J. Lobo, P. Lucas, J. Dias, and Traca, “Inertial navigation sys- tem for mobile land vehicles,” in Industrial Electronics, 1995. ISIE ’95., Proceedings of the IEEE International Symposium on, vol. 2, 1995, pp. 843–848 vol.2. [5] E. Nebot and H. Durrant-Whyte, “Initial calibration and alignment of low-cost inertial navigation units for land vehicle applications,” Journal of Robotic Systems, vol. 16, no. 2, pp. 81–92, 1999. [6] K. Yamanaka, M. Kanbara, and N. Yokoya, “Localization of walking or running user with wearable 3d position sensor,” In- ternational Conference on Artificial Reality and Telexistence, vol. 0, pp. 39–45, 2007. [7] A. Hamaguchi, M. Kanbara, and N. Yokoya, “User localiza- tion using wearable electromagnetic tracker and orientation sensor,” Wearable Computers, IEEE International Sympo- sium, vol. 0, pp. 55–58, 2006. [8] C. Randell, C. Djiallis, and H. Muller, “Personal position measurement using dead reckoning,” in Proceedings of the 7th IEEE International Symposium on Wearable Computers, ser. ISWC ’03. Washington, DC, USA: IEEE Computer Society, 2003, pp. 166–. [9] E. Foxlin, “Pedestrian tracking with shoe-mounted inertial sensors,” IEEE Computer Graphics and Applications, vol. 25, pp. 38–46, 2005. [10] S. Godha and G. Lachapelle, “Foot mounted inertial system for pedestrian navigation,” Measurement Science and Tech- nology, vol. 19, no. 7, p. 075202, 2008. [11] O. Woodman and R. Harle, “Pedestrian localisation for indoor environments,” in Proceedings of the 10th international con- ference on Ubiquitous computing, ser. UbiComp ’08. New York, NY, USA: ACM, 2008, pp. 114–123. [12] J. Dixon-Warren, “Motion sensing in the iphone 4: Mems [Online]. http://www.memsinvestorjournal.com/2010/12/ accelerometer,” MEMS Investor Journal, 2010. Available: motion-sensing-in-the-iphone-4-mems-accelerometer.html [13] P. Gallais, Atmospheric re-entry vehicle mechanics. Springer Berlin Heidelberg, 2007, pp. 96–103. [14] Apple Inc., Website, http://developer.apple.com/ iphone/library/samplecode/accelerometergraph/Listings/ AccelerometerFilter\ m.html visited on July 13th 2010. [15] G. Welch and G. Bishop, “An introduction to the kalman filter,” Chapel Hill, NC, USA, Tech. Rep., 1995. [16] A. P. A. Mohinder S. Grewal, Kalman Filtering: Theory and Practice Using MatLab, 2nd ed. John Wiley and Sons, 2001.