2022年山东临沂中考数学试题及答案.doc-资料库

第1页 / 共8页

第2页 / 共8页

第3页 / 共8页

第4页 / 共8页

第5页 / 共8页

第6页 / 共8页

第7页 / 共8页

第8页 / 共8页

2022 年山东临沂中考数学试题及答案一、选择题（本大题共 12 小题，每小题 3 分，共 36 分）在每小题所给出的四个选项中，只有一项是符合题目要求的． 1．﹣2 的相反数是（） A．±2 B．﹣ C．2 D． 2．剪纸艺术是最古老的中国民间艺术之一，先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录．鱼与“余”同音，寓意生活富裕、年年有余，是剪纸艺术中很受喜爱的主题．以下关于鱼的剪纸中，既是轴对称图形又是中心对称图形的是（） A． C． B． D． 3．计算 a（a+1）﹣a的结果是（） A．1 B．a2 C．a2+2a D．a2﹣a+1 4．如图，A，B位于数轴上原点两侧，且 OB＝2OA．若点 B表示的数是 6，则点 A表示的数是（） A．﹣2 B．﹣3 C．﹣4 D．﹣5 5．如图所示的三棱柱的展开图不可能是（） 6．如图是某一水塘边的警示牌，牌面是五边形，这个五边形的内角和是（）

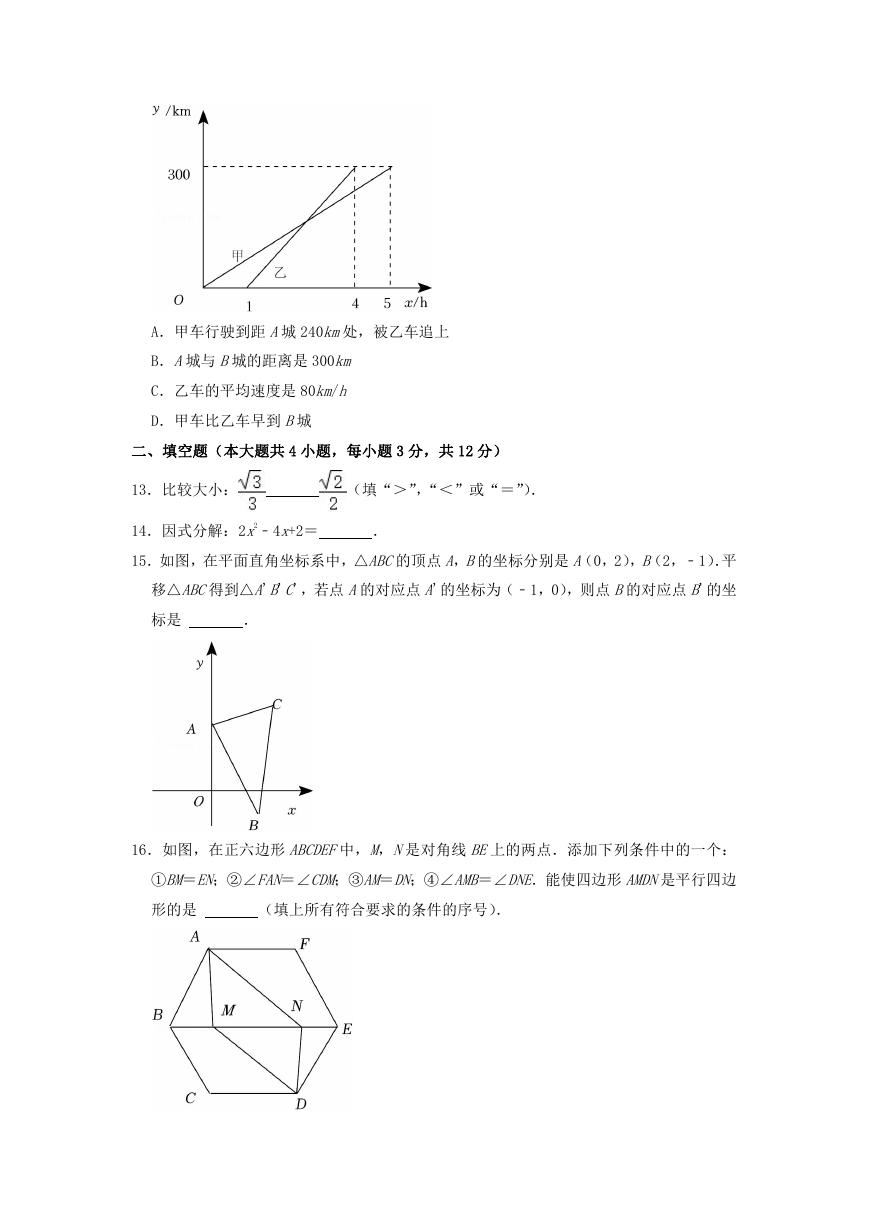
A．900° B．720° C．540° D．360° 7．满足 m＞| ﹣1|的整数 m的值可能是（） A．3 B．2 C．1 D．0 8．方程 x2﹣2x﹣24＝0 的根是（） A．x1＝6，x2＝4 C．x1＝﹣6，x2＝4 B．x1＝6，x2＝﹣4 D．x1＝﹣6，x2＝﹣4 9．为做好疫情防控工作，某学校门口设置了 A，B两条体温快速检测通道，该校同学王明和李强均从 A通道入校的概率是（） A． B． C． D． 10．如图，在△ABC中，DE∥BC，＝，若 AC＝6，则 EC＝（） A． B． C． D． 11．将 5kg浓度为 98%的酒精．稀释为 75%的酒精．设需要加水 xkg，根据题意可列方程为（） A．0.98×5＝0.75x C．0.75×5＝0.98x B． D．＝0.75 ＝0.98 12．甲、乙两车从 A城出发前往 B城，在整个行程中，汽车离开 A城的距离 y（单位：km）与时间 x（单位：h）的对应关系如图所示，下列说法中不正确的是（）

A．甲车行驶到距 A城 240km处，被乙车追上 B．A城与 B城的距离是 300km C．乙车的平均速度是 80km/h D．甲车比乙车早到 B城二、填空题（本大题共 4 小题，每小题 3 分，共 12 分） 13．比较大小：（填“＞”，“＜”或“＝”）． 14．因式分解：2x2﹣4x+2＝． 15．如图，在平面直角坐标系中，△ABC的顶点 A，B的坐标分别是 A（0，2），B（2，﹣1）．平移△ABC得到△A'B'C'，若点 A的对应点 A'的坐标为（﹣1，0），则点 B的对应点 B'的坐标是． 16．如图，在正六边形 ABCDEF中，M，N是对角线 BE上的两点．添加下列条件中的一个： ①BM＝EN；②∠FAN＝∠CDM；③AM＝DN；④∠AMB＝∠DNE．能使四边形 AMDN是平行四边形的是（填上所有符合要求的条件的序号）．

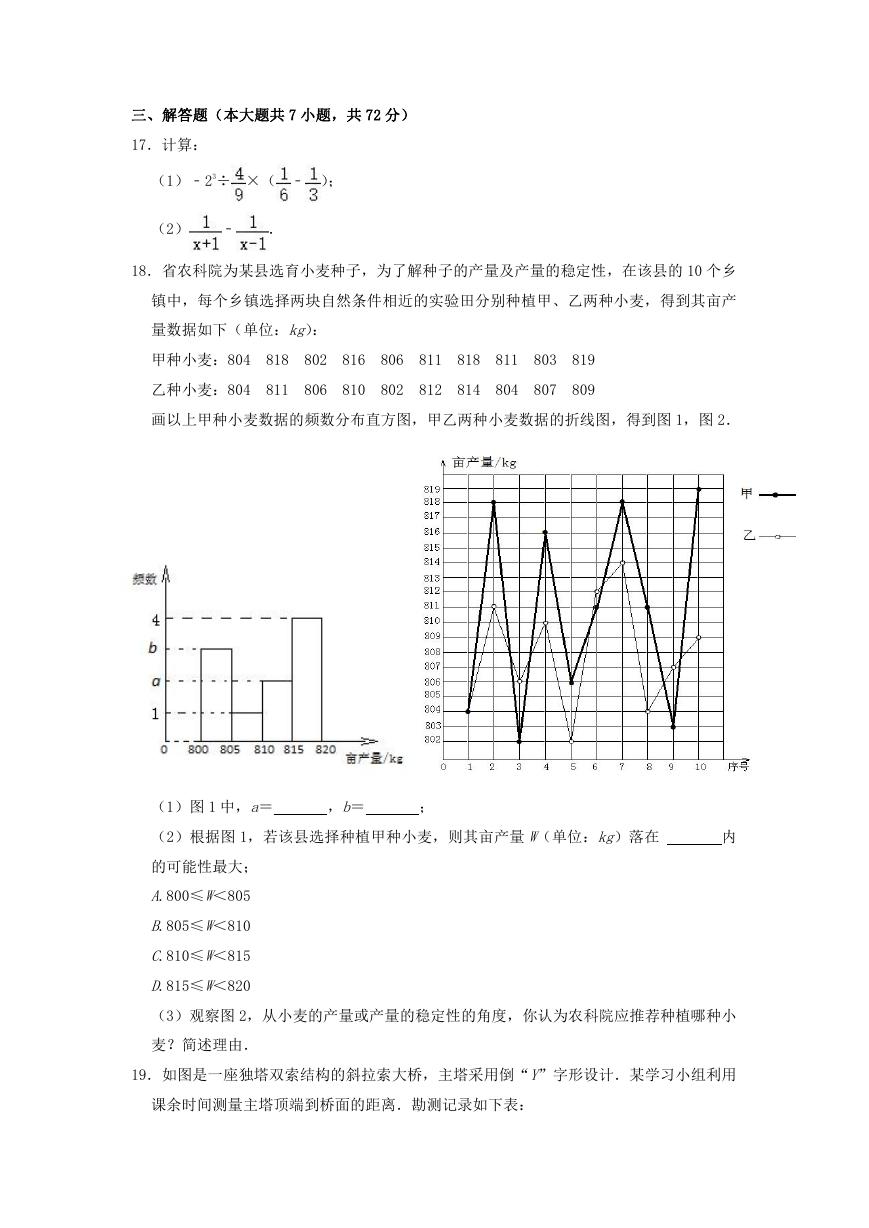
三、解答题（本大题共 7 小题，共 72 分） 17．计算：（1）﹣23÷ ×（ ﹣ ）；（2） ﹣ ． 18．省农科院为某县选育小麦种子，为了解种子的产量及产量的稳定性，在该县的 10 个乡镇中，每个乡镇选择两块自然条件相近的实验田分别种植甲、乙两种小麦，得到其亩产量数据如下（单位：kg）：甲种小麦：804 818 802 816 806 811 818 811 803 819 乙种小麦：804 811 806 810 802 812 814 804 807 809 画以上甲种小麦数据的频数分布直方图，甲乙两种小麦数据的折线图，得到图 1，图 2．图 1 图 2 （1）图 1 中，a＝，b＝；（2）根据图 1，若该县选择种植甲种小麦，则其亩产量 W（单位：kg）落在内的可能性最大； A.800≤W＜805 B.805≤W＜810 C.810≤W＜815 D.815≤W＜820 （3）观察图 2，从小麦的产量或产量的稳定性的角度，你认为农科院应推荐种植哪种小麦？简述理由． 19．如图是一座独塔双索结构的斜拉索大桥，主塔采用倒“Y”字形设计．某学习小组利用课余时间测量主塔顶端到桥面的距离．勘测记录如下表：

活动内容成员测量工具测量示意图测量数据测量主塔顶端到桥面的距离组长：×××组员×××××××××××× 测角仪，皮尺等说明：左图为斜拉索桥的侧面示意图，点 A，C，D，B在同一条直线上，EF⊥AB，点 A， C分别与点 B，D关于直线 EF 对称． 28° 84m 12m ∠A的大小 AC的长度 CD的长度请利用表中提供的信息，求主塔顶端 E到 AB的距离（参考数据：sin28°≈0.47，cos28° ≈0.88，tan28°≈0.53）． 20．杠杆原理在生活中被广泛应用（杠杆原理：阻力×阻力臂＝动力×动力臂），小明利用这一原理制作了一个称量物体质量的简易“秤”（如图 1）．制作方法如下：第一步：在一根匀质细木杆上标上均匀的刻度（单位长度 1cm），确定支点 O，并用细麻绳固定，在支点 O左侧 2cm的 A处固定一个金属吊钩，作为秤钩；第二步：取一个质量为 0.5kg的金属物体作为秤砣．（1）图 1 中，把重物挂在秤钩上，秤驼挂在支点 O右侧的 B处，秤杆平衡，就能称得重物的质量．当重物的质量变化时，OB的长度随之变化．设重物的质量为 xkg，OB的长为 ycm．写出 y关于 x的函数解析式；若 0＜y＜48，求 x的取值范围．

图 1 图 2 （2）调换秤砣与重物的位置，把秤驼挂在秤钩上，重物挂在支点 O右侧的 B处，使秤杆平衡，如图 2．设重物的质量为 xkg，OB的长为 ycm，写出 y关于 x的函数解析式，完成下表，画出该函数的图象． x/kg y/cm …… …… 0.25 0.5 1 2 4 …… …… 21．如图，AB是⊙O的切线，B为切点，直线 AO交⊙O于 C，D两点，连接 BC，BD．过圆心 O作 BC的平行线，分别交 AB的延长线、⊙O及 BD于点 E，F，G．（1）求证：∠D＝∠E；（2）若 F是 OE的中点，⊙O的半径为 3，求阴影部分的面积． 22．已知△ABC是等边三角形，点 B，D关于直线 AC对称，连接 AD，CD．（1）求证：四边形 ABCD是菱形；（2）在线段 AC上任取一点 P（端点除外），连接 PD．将线段 PD绕点 P逆时针旋转，使点 D落在 BA延长线上的点 Q处．请探究：当点 P在线段 AC上的位置发生变化时，∠DPQ 的大小是否发生变化？说明理由．（3）在满足（2）的条件下，探究线段 AQ与 CP之间的数量关系，并加以证明．

23．第二十四届冬奥会在北京成功举办，我国选手在跳台滑雪项目中夺得金牌．在该项目中，运动员首先沿着跳台助滑道飞速下滑，然后在起跳点腾空，身体在空中飞行至着陆坡着陆，再滑行到停止区终止．本项目主要考核运动员的飞行距离和动作姿态，某数学兴趣小组对该项目中的数学问题进行了深入研究：如图为该兴趣小组绘制的赛道截面图，以停止区 CD所在水平线为 x轴，过起跳点 A与 x 轴垂直的直线为 y轴，O为坐标原点，建立平面直角坐标系．着陆坡 AC的坡角为 30°， OA＝65m，某运动员在 A处起跳腾空后，飞行至着陆坡的 B处着陆，AB＝100m．在空中飞行过程中，运动员到 x轴的距离 y（m）与水平方向移动的距离 x（m）具备二次函数关系，其解析式为 y＝﹣ x2+bx+c．（1）求 b，c的值；（2）进一步研究发现，运动员在飞行过程中，其水平方向移动的距离 x（m）与飞行时间 t（s）具备一次函数关系，当运动员在起跳点腾空时，t＝0，x＝0；空中飞行 5s后着陆． ①求 x关于 t的函数解析式； ②当 t为何值时，运动员离着陆坡的竖直距离 h最大，最大值是多少？一、选择：参考答案

1-12 CDBBD CABAC BD 二、填空： 13.< 14.  2 三、解答题： 2 1x  15. 1, 3  16.①②④ 17.（1）3 2 2  （2）  x 1 18.（1） 2a  ， 3b  （2）D （3）甲产量较高，但稳定性差，乙产量低，但稳定从产量角度选择甲，从稳定性角度选乙. 19.47.7m 20.（1） 0 x  1 x （2）  y 12 图略 21.（1）证明：连接 OB 得证 D    E （2） S   3 2 9 3 8 22.（1）证四边形 ABCD为菱形（2） DPQ （3）连接QD .证 CDP △ ≌ 大小不变，连接 PB 可得 ADQ △ 60  DPQ  得CP AQ 23.（1） b  3 2 ， 65 c  （2）①  10 3 0 t   t 5 x  5 s 2 ② t  时， h 最大，为  125 m 4 .

资料库

2022年山东临沂中考数学试题及答案.doc

相关推荐

中考

热门标签

最新资料