哈工大数电习题答案.doc

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：5.91M 资料格式：doc 举报版权申诉

u012260509-6326801-4744302542861323468.doc.pdf-第1页.png

第1页 / 共48页

u012260509-6326801-4744302542861323468.doc.pdf-第2页.png

第2页 / 共48页

u012260509-6326801-4744302542861323468.doc.pdf-第3页.png

第3页 / 共48页

u012260509-6326801-4744302542861323468.doc.pdf-第4页.png

第4页 / 共48页

u012260509-6326801-4744302542861323468.doc.pdf-第5页.png

第5页 / 共48页

u012260509-6326801-4744302542861323468.doc.pdf-第6页.png

第6页 / 共48页

u012260509-6326801-4744302542861323468.doc.pdf-第7页.png

第7页 / 共48页

u012260509-6326801-4744302542861323468.doc.pdf-第8页.png

第8页 / 共48页

【7-2】如图7-2(a)所示CMOS电路，已知各输入波形A、B、C如图(b)所示。R=10k(请画

(a)

图7-2 题7-2电路图

解：当C=0时，输出端逻辑表达式为F=；当C=1时，

图7-3 题7-3图

解：F1=，F2=1，F3=

图7-6题7-6的输入波形图

解：当时，；

当时，。

于是，逻辑表达式

F的波形见图7-6(c)所示。

图7-6(c) 题7-6的输出波形图

图7-8(b) 题7-8的电路图

图 7-10(b) 题7-10电压传输

H M L

D J

图 9-2 题9-2的输入波形图及输出波形

6.1 对课程内容掌握程度的建议第 6 章逻辑代数基础章节 6.1 概述 6.2 逻辑运算 6.3 形式定理 6.4 基本规则课程内容掌握程度 C B A 数字信号，脉冲信号正逻辑和负逻辑基本逻辑运算组合逻辑运算 17 个形式定理代入规则反演规则对偶规则展开规则 6.5 用代数法化简逻辑式 6.6 最小项和最大项最小项 6.7 卡诺图化简法卡诺图化简法 6.2 授课的几点建议 6.2.1 基本逻辑关系的描述用代数法化简逻辑式最大项基本逻辑关系有“与”、“或”、“非”三种，在本教材中采用文字叙述和常开触点、常闭触点的串、并联等形式来加以描述。还有一种描述逻辑关系的图，称为文氏图（Venn diagram）。图 6.1(a)圆圈内是 A，圆圈外是 A ；图 6.1(b)圆圈 A 与圆圈 B 相交的部分是 A、B 的与逻辑，即 AB；图 6.1(c)圆圈 A 与圆圈 B 所有的部分是 A、B 的或逻辑，即 A+B。与逻辑 AB 也称为 A 与 B 的交集（intersection）；或逻辑 A+B 也称为 A 和 B 的并集（union）。 A A AB A B A+B A B (a) 单变量的文氏图 (b) 与逻辑的文氏图 (c) 或逻辑的文氏图图 6.1 文氏图 6.2.2 正逻辑和负逻辑的关系正逻辑是将双值逻辑的高电平 H 定义为“1”，代表有信号；低电平 L 定义为“0”，代表无信号。负逻辑是将双值逻辑的高电平 H 定义为“0”，代表无信号；低电平 L 定义为“1”，代表有信号。正逻辑和负逻辑对信号有无的定义正好相反，就好象“左”、“右”的规定一样，设正逻辑符合现在习惯的规定，而负逻辑正好反过来，把现在是“左”，定义为“右”，把现在是“右”，定义为“左”。关于正、负逻辑的真值表，以两个变量为例，见表 6.1。表 6.1 输入变量 A L L H H B L H L H 输出 Y L L L H 正逻辑 B 0 1 0 1 Y 0 0 0 1 A 0 0 1 1 A 1 1 0 0 负逻辑 B 1 0 1 0 Y 1 1 1 0 由表 6.1 可以看出，对正逻辑的约定，表中相当是与逻辑；对负逻辑约定，则相当是或逻辑。所以正逻辑的“与”相当负逻辑的“或”；正逻辑的“或”相当负逻辑的“与”。正与和负或只是形式上的不同，不改变问题的实质。 6.2.3 形式定理本书介绍了 17 个形式定理，分成五类。需要说明的是，许多书上对这些形式定理有各自的名称，可能是翻译上的缘故，有一些不太贴切，为此，将形式定理分成 5 种形式表述，更便于记忆。所以称为形式定理，是因为这些定理在逻辑关系的形式上虽然不同，但实质上是相等的。形式定理主要用于逻辑式的化简，或者在形式上对逻辑式进行变换，它有以下五种类型： 1

1．变量与常量之间的关系；2．变量自身之间的关系；3．与或型的逻辑关系；4．或与型的逻辑关系；5．求反的逻辑关系——摩根（Morgan）定理。 6.2.3.1 变量与常量之间的关系变量与常量之间的关系可分为与逻辑和或逻辑两种形式，共四个。定理 1： A0 =0 定理 3： A∙1 =A 定理 2： A+1=1 定理 4： A+0=A 6.2.3.2 变量自身之间的关系变量自身之间的关系也可分为与逻辑和或逻辑两种形式，共四个。定理 5： A∙A =A 定理 7： A∙ A =0 定理 6： A+A =A 定理 8： A+ A =1 6.2.3.3 与或型和或与型的逻辑关系与或型和或与型的定理有三对，它们是定理 9： A +A B = A 定理 11： A+ A B =A+B 定理 13： AB+ A C+BC =AB+ A C 定理 10： A（A + B）= A 定理 12： A（ A +B）=AB 定理 14： (A+B)( A +C)(B+C)=(A+B)( A +C ) 6.2.3.4 求反的逻辑关系 ABA 定理 15： B  定理 16： AA  以上介绍了十七个形式定理，只须熟记其中的一半，利用对偶规则即可得出另一半。形式定理的证明一般采用代数法，即用已经被证明的定理去证明那些需要证明的定理；二是所谓的真值法，因为对于双值逻辑系统，每一个逻辑变量只有“0”和“1”，对于 2 个逻辑变量，只有 4 种可能，对于 3 个逻辑变量，只有 8 种可能，…，所以可以将逻辑变量的真值代入形式定理一一验证。不过变量数较多时也很不方便。利用文氏图也可以证明形式定理，例如摩根定理，图 6.2 表示了这一过程。 . BABA 定理 17：证明 BA 是 B  ABA 。图 6.2(a)和图 6.2 (d)完全一样，由此证明了，图 6.2(a)是 BA  ，正好是图 6.1 (b)的反；图 6.2 (b)是 A ；图 6.2 (c) 是 B ；图 6.2 (d) AB A B A A B ABA  B B B A A+B A B (a) (b) (c) 图 6.2 用文氏图证明摩根定理 (d) 6.2.4 最小项、最大项及其性质最小项在逻辑函数的变换和化简中具有重要意义，在可编程逻辑器件、半导体存储器中有重要应用。同一逻辑关系的逻辑函数具有多样性，但同一逻辑关系的逻辑函数它都是由若干个最小项构成的，它的多样性实际上是这些最小项的不同组合而已。任一逻辑函数都是若干个最小项之和，即立即函数 Y Y  im Y  称为逻辑函数的与或标准型。它的对偶式的形式是若干个最大项之积 im 称为逻辑函数的或与标准型。最小项的主要性质如下： 1．当有二进制码输入时，最小项对每一种输入被选中的特点是只有一个最小项是“1”，其余最小项都是 “0”，即所谓 N（2n）中取一个“1”。 2．全部最小项之和恒等于“1”。 3．两个最小项之积恒等于“0”。 m3+m2+m1+m0=1 mimj=0（ j 4．若干个最小项之和等于其余最小项和之反。例如： m mm   1 5．最小项的反是最大项，最大项的反是最小项。 6．当有二进制码输入时，最大项对每一种输入被选中的特点是只有一个最大项是“0”，其余最大项都是 mm 1 m i  ） m m     2 3 3 0 2 0 “1”，即所谓 N（2n）中取一个“0”。最大项与最小项有对偶的关系，在性质上也有对偶关系，例如性质 1 和性质 6 是对偶关系；性质 3，两个 2

最小项之积恒等于“0”，那么，两个最大项之和恒等于“1”，等等，不一一举例。 6.2.5 逻辑函数的化简与变换 6.2.5.1 逻辑函数的化简逻辑函数的化简是为了在具体实现该逻辑电路时，在硬件上节省集成电路。以与或逻辑式为标准，逻辑式的与项最少，与项中的变量数最少者为最简。实际上因为任何一个逻辑函数都可以转换为与或标准型，即最小项之和的形式。最小项之间以不同的方式搭配，逻辑函数就有不同的形式，造成了逻辑函数的多样性。所以，逻辑函数的化简就是寻找最小项的某一种搭配方式，以获得最简与或式。逻辑函数的化简一般有两种方法，代数法化简和卡诺图化简。代数法化简就是运用 17 个形式定理和一些规则、性质对逻辑函数进行化简，这种化简方法称为代数法化简。代数法化简的优点是它的使用不受任何条件的限制，但由于这种方法没有固定的步骤可循，所以在化简一些复杂的逻辑函数时不仅需要熟练地运用各种定理和规则，而且需要有一定的运算技巧和经验。逻辑函数的化简是本章的重点内容。卡诺图化简法是一种在方格图形上进行最小项重新组合的方法。这种方法简单、直观，而且有一定的化简步骤可循。而且化简过程不易出现差错。变量数在 5 个以下时，用卡诺图法化简比较实用。逻辑代数是数字电路的数学工具，涉及数字电子技术的方方面面，例如在数字电路设计和分析时要经常使用各种化简方法，是必须掌握的内容。 6.2.5.2 逻辑函数的变换用最简与或式实现硬件电路时，往往需要解决一些问题，希望采用同一种逻辑关系的集成电路，以利维修；希望采用与或逻辑关系以外的集成电路，如与非、或非、与或非等器件来实现硬件电路；希望输入没有反变量等等。这就需要进行逻辑函数的变换，现举例说明。解：异或函数例 6.1:将异或函数   符合与或函数的最简条件，如果将其直接实现，并消除输入反变量，如图 6.3 所示，需要一片反相器 74LS04，一片 2 输入与门 74LS08，一片 2 输入或门 74LS32，共三片集成电路。如果采用与非门，并消除输入反变量，如图 6.4 所示，只需要一片 2 输入与非门 74LS00，或者使用专门的异或门。用尽可能少的集成电路芯片实现。 F BABA BABA   F A B B A 1 1 & & B A 1 F A B & 例 6.2：将最简与或逻辑式 BACBBA 解：查手册，可以用一片 74LS51 实现，如图 6.5 所示。 CBBA F     图 6.3 F  BC  用与或非门实现。 & F & & 图 6.4 B & 1 “0” C A & 1 F 图 6.5 关于逻辑函数的变换不一定在课堂上大讲特讲，可以结合实验进行，但是教师要心中有数。习题【6-1】填空 1．与模拟信号相比，数字信号的特点是它的离散性。一个数字信号只有两种取值分别表示为 0 和 1 。 2．布尔代数中有三种最基本运算：与、或和非，在此基础上又派生出四种基本运算，分别为与非、或非、与或非和异或。 3．与运算的法则可概述为：有“0”出 0 ，全“1”出 1；类似地或运算的法则为有”1”出”1”，全”0” 出”0” 。 4．摩根定理表示为： A B 5．函数表达式 Y= AB C D = A B ； A B = A B 。  ，则其对偶式为 Y   ( A B C D  。 ) 6．根据反演规则，若 Y= AB C D C  ，则Y    ( CDCBA   )  。 3

7．指出下列各式中哪些是四变量 A B C D 的最小项和最大项。在最小项后的（）里填入 mi，在最大项后的（）里填入 Mi，其它填×（i 为最小项或最大项的序号）。 (1) A+B+D (× )； (2) ABCD (m7 )； (5) A B C D (4)AB(C+D) 8．函数式 F=AB+BC+CD 写成最小项之和的形式结果应为 m (3,6,7,11,12,13,14,15),写成最大项之积的形 ABC ( × )； (M9 ) ； (6) A+B+CD (× ); (×)； (3)    10．已知有四个逻辑变量，它们能组成的最大项的个数为 16 个，这四个逻辑变量的任意两个最小 9．对逻辑运算判断下述说法是否正确，正确者在其后（ √ ）内打对号，反之打×。式结果应为 M( 0,1,2,4,5,8,9,10 ) （1）若 X+Y=X+Z，则 Y=Z；( × ) （2）若 XY=XZ，则 Y=Z；( × ) （3）若 X  Y=X  Z，则 Y=Z；(√ )    )    =AD  =1  (        = A BC      AB  CBA 项之积恒为 “0 ” 。【6-2】用代数法化简下列各式 (1) F1 = ABC AB (2) F2 = ABCD ABD ACD (3) F3 = AC ABC ACD CD  =A+CD ) ( A B C (4) F4 = A B C A B C     (5) F5= AC AB BCD BEC DEC = AB AC BD EC     = A BC CD (6) F6 = AB CD ABC AD ABC    (7) F7 = AC AB BCD BD ABD ABCD = A BD BD     = ABCD ABCD ABCD ABCD  DBDBCACA  (8) F8 =  ) ( CD BABABA F    (9) 9 = A D B C  F CD CDB   10 (10) 【6-3】用卡诺图化简下列各式 (1) F1 = BC AB ABC (2) F2 = AB BC BC (3) F3= AC AC BC BC = AB AC BC (4) F4 = ABC ABD ACD CD ABC ACD   (5) F5 = ABC AC ABD = AB AC BD (6) F6= AB CD ABC AD ABC    (7) F7 = AC AB BCD BD ABD ABCD = A BD BD  (8) F8 = AC AC BD BD  (9) F9 = A C D BCD ACD ABCD (10) F10= AC AB BCD BEC DEC  = A BC CD        )    = CD CD  = AB AC BD EC = BCD ACD = A B  或 AB AC BC   = AB C = A D                    )(             = ABCD ABCD ABCD ABCD ( BC A 0 0 0 1 1 1 01 11 1 10 1 1 0 0 B C A 0 1 1 11 1 01 1 1 10 1 1 (1) (3) B C A 0 0 0 1 01 1 11 1 1 10 1 1 (2) 1 0 0 B C A 0 1 1 11 1 01 1 1 10 1 1 (3) 4

CD A B 00 0 0 1 01 11 10 1 1 1 01 11 1 1 1 1 10 1 1 1 1 CD A B 00 0 0 1 01 11 10 1 1 1 01 11 1 10 1 1 1 1 1 1 1 0 0 CD A B 00 10 01 1 11 1 01 11 10 1 1 1 1 1 1 (4) (5) CD A B 00 00 1 01 11 10 1 1 01 1 1 1 11 1 1 1 0 0 CD A B 00 01 11 10 E=1 10 1 1 1 01 1 1 1 1 11 (7) 10 1 1 1 1 10 1 1 0 1 11 1 01 1 00 1 (9) (6) (8) CD A B 00 0 0 1 E=0 01 1 11 1 01 11 10 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 (10)     【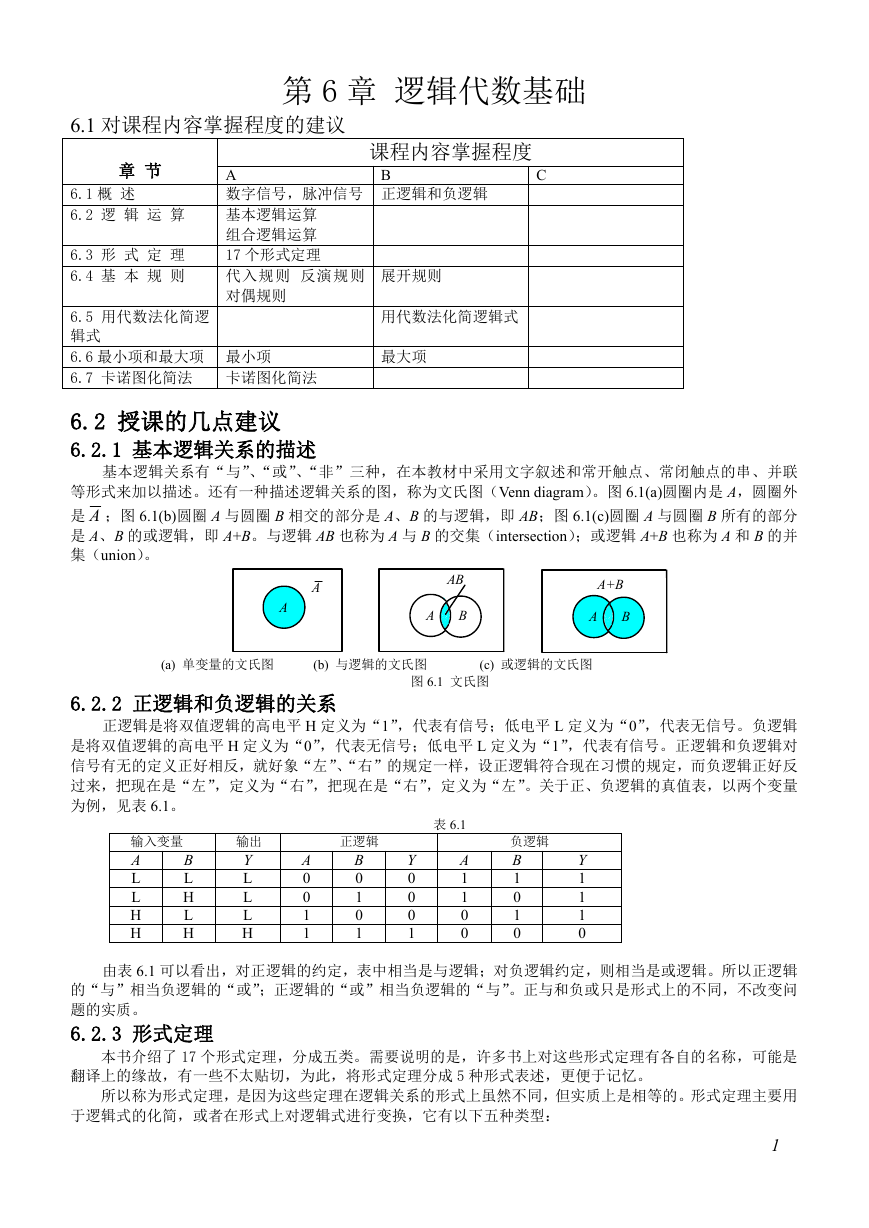6-4】用卡诺图化简下列各式 0 1 2 5 6 7 , , , ) (1) F1(A,B,C)= m( , ,  0 1 2 3 4 6 7 8 9 10 1114 , , , , (2)F2(A,B,C,D)= m( , , ) = AC AD B CD , , , , 0 1 4 6 8 9 10 12 1314 15 (3)F3(A,B,C,D)= m( , ,, ) = AB BC AD BD  (4) F4 (A,B,C,D)= M M1 = A BC BC D   = 7  )31,30,29,27,25,22,20,17,16,15,11,8,7,6,4,3,0( m (5) EABC ABCD ACD EBCD EAD EAB ECDB  = AB AC BC , , ,  (5 DCBAEF       , , m m m m 1 7 ,   7 1    , , , , )  , , ,   CD A B 00 01 11 10  0 0 1 1 01 1 11 1 1 1 1 1 10 1 1 1 1 00 1 BC A 0 1 01 11 1 1 1 10 1 1 (1) (2) 5

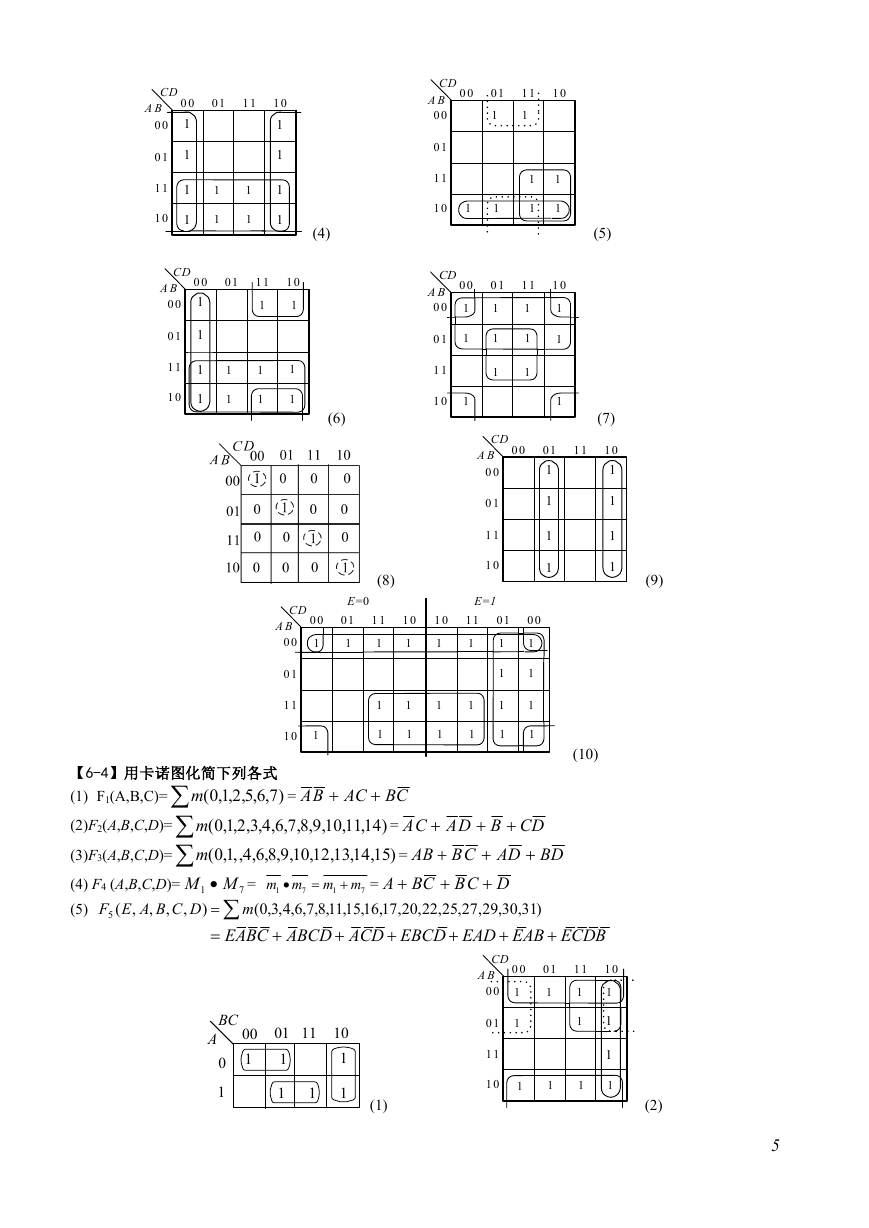
CD A B 00 0 0 1 01 11 10 1 1 1 01 1 1 1 11 10 1 1 1 1 CD A B 00 01 11 10 0 0 1 1 1 CD A B 00 0 0 1 01 11 10 1 1 1 01 1 1 1 11 1 10 1 1 1 1 1 1 (4) (3) E=0 01 11 1 1 1 1 E=1 10 0 0 01 1 1 1 1 1 10 1 1 11 1 1 1 (5) , 【6-5】用卡诺图化简下列带有约束条件的逻辑函数   ( , , ) 0 1 2 1314 15 ( , , , 3 6 8 9 1112 ) , （1）P1 (A,B,C,D)= m d ( ) ACD = AC BD BCD  或   ( , ) , 0 2 3 4 5 6 1112 (2) P2(A,B,C,D)= m = BC BC D     ( 或 (3) P3 = A C D ABCD ABCD ) ABD = AD ACD BCD ,  , , , (AB+AC=0) , ,     , d , , ( , ) 8 9 10 1314 15 , , , CD A B 00 00 01 × × 11 1 CD A B 00 00 1 01 11 10 1 1 10 × 1 × ×× 1 1 (1)  11 1 01 1 × × × × 1 (2) 1 1 01 11 10 10 1 1 × × CD A B 00 01 11 10 01 11 00 1 1 × × × 1 × (3) 10 1 × × 【6-6】列出逻辑函数  BAF A 0 0 0 0 1 1 1 1 CAB B 0 0 1 1 0 0 1 1 的真值表。 F C 0 0 0 1 0 1 1 1 0 0 0 1 0 1 0 1 【6-7】写出下列函数的反函数 F ，并将其化成最简与或式。 1． 2． 3． 4． 1． 2．解： )  )(     )( )( C  )( )( ( F ABDCBDA   1 ( ) F BA BCD ACECBE   2 F DACBA  3  ( ) CBA F  4 F AD C 1 ECA AB F 2    DCB   ) ( 6

【6-8】用对偶规则，写出下列函数的对偶式 F  ，再将 F  化为最简与或式。 ABC BC CD     3F   AB C D 3． 4． F 3 F 4 BA AC DA    DCCB CBADAB      ) ) CACB    4F   )(   )( )( CD )(   )(   CDB  AB   DCBA  ( A C B C D A B D ABC  ( A B A C B C C D  CBA F  1． 1 F  2． 2 F  3． 3 F  4． 4 F 5． 5 解：题中各函数对偶函数的最简与或式如下： 1． 2． 3． 4． 5． CBACBA DCADBA AC   DBA 1 F 2 F 3 F DCAB   F 5 【6-9】已知逻辑函数 CBAF  解： ACBACBA F  BA  . . F A B C A B C A B C        A B C A B C A B C   G       . . , G=A⊙B⊙C，试用代数法证明： GF  。  BC 【6-10】证明下列逻辑式相等： BACBCABACBCA   A C BC AB A BC A BC ABC ABC ABC ABC   AC BC AB             解：【6-11】用卡诺图化简下列逻辑式，说明可能有几种最简结果。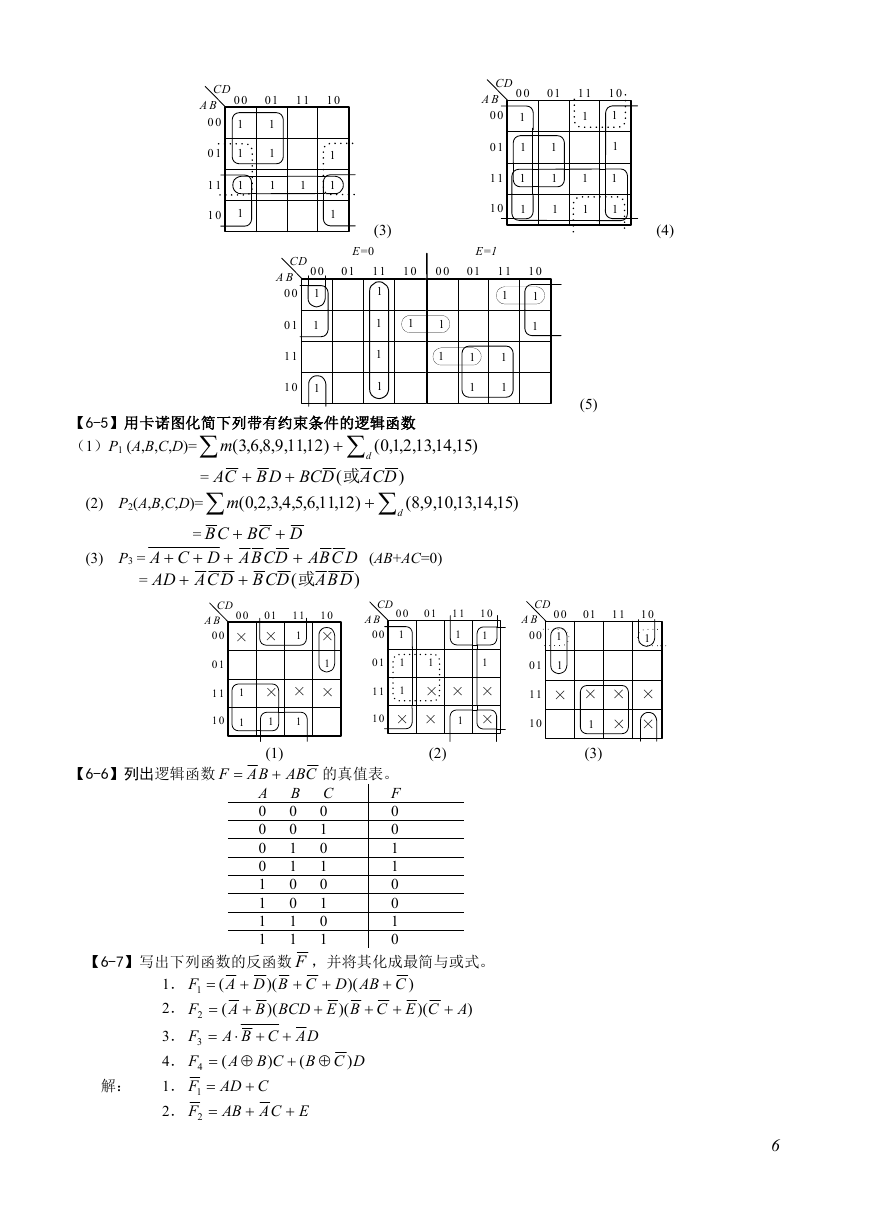 CAADDCCBBAF      解： 00 CD A B 00 01 11 10 1 1 1 01 1 11 1 10 1 1 1 1 1 1 1 1 1 四种： F 1 DBCADCBA   00 CD A B 00 01 11 10 1 1 1 F 2 01 1 1 1 1 11 1 1 1 10 1 1 1 1 CBDADCBA    00 CD A B 00 01 11 10 1 1 1 01 1 11 1 10 1 1 1 1 1 1 1 1 1  CD A B 0 0 0 1 1 1 1 0 0 0 01 1 11 1 10 1 1 1 1 1 1 1 1 1 1 1 1 F 3 CBDADCBA  【6-12】已知: Y1 = AB AC BD Y1 Y 2 ，   用卡诺图分别求出Y Y1  ， 2 DBCADCBA Y2 = ABCD ACD BCD BC  2 。 F 4   Y 1 Y      7

解：先画出 Y1 和 Y2 的卡诺图，根据与、或和异或运算规则直接画出Y Y1 2  ，Y Y1 2 ，Y 1 2 的卡诺图， Y 再化简得到它们的逻辑表达式： 10 1 1 1 0 0 CD A B 00 01 1 11 1 01 11 10 1 1 1 1 1 1 1Y 00 01 CD A B 00 11 1 10 1 01 11 10 1 1 1 1 1 2Y 0 0 01 CD A B 00 11 1 10 1 01 11 10 1 1 1 1 0 0 CD A B 00 01 1 11 1 10 1 01 11 10 1 1 1 1 1 1 1 1 1 0 0 CD A B 00 01 1 11 10 01 11 10 1 1 1 1 1 1Y 2Y+ 1Y 2Y+ 1Y 2Y = ABD ABC CD  = AB C BD Y Y1  2 Y1 Y 2 2 = ABCD ABC BCD ACD Y Y 1       第 7 章集成逻辑门 7.1 对课程内容掌握程度的建议章节 A 7.1 半导体二极管和晶体管的开关特性 7.2 基本逻辑门电路逻辑门电路符号 7.3 标准 TTL 与非门电路标准 TTL 与非门电路 7.4 其他类型 TTL 门其他类型 TTL 门 7.5 CMOS 逻辑门 CMOS 逻辑门 7.6 国标数字集成电路系列介绍课程内容掌握程度 B 半导体二极管和晶体管的开关特性 C 国标数字集成电路系列介绍 7.2 授课的几点建议 7.2.1 标准 TTL 与非门电路的结构标准 TTL 与非门如图 7.1 所示，TTL 与非门的重点是逻辑关系、特性曲线和参数，内部电路为曲线和参数服务，通过内部电路以便更好地了解曲线和参数，对集成数字电路内部结构做一般了解。 TTL 与非门由 8

分享到：

赞收藏

资料库

哈工大数电习题答案.doc

相关推荐

课程资源

热门标签

最新资料