2016年四川省资阳市中考数学真题及答案.doc-资料库

2016 年四川省资阳市中考数学真题及答案一、选择题．（本大题共 10 小题，每小题 3 分，共 30 分） 1． ﹣ 2 的倒数是（） A． ﹣ B． C． ﹣ 2 D． 2 2．下列运算正确的是（ A． x 4+x 2 =x 6B． x 2 •x 3=x 6 C．（ x 2） 3 =x 6D． x 2﹣ y 2=（ x﹣ y） 2 3．如图是一个正方体纸盒的外表面展开图，则这个正方体是（）） A． B． C． D． 4．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有 0.000000076 克，将数 0.000 000076 用科学记数法表示为（ A． 7.6 × 10 ﹣ 9B． 7.6 × 10 ﹣ 8C． 7.6 × 10 9D． 7.6 × 10 8 5． A． 2 和 3 B． 3 和 4 C ． 4 和 5 D． 5 和 6 6．我市某中学九年级（ 1）班开展 “阳光体育运动 ” ，决定自筹资金为班级购买体育器材，全班 50 名同学筹款情况如下表：的运算结果应在哪两个连续整数之间（））筹款金额（元）人数 5 3 10 7 15 11 20 11 25 13 30 5 则该班同学筹款金额的众数和中位数分别是（ A． 11 ， 20 B． 25 ， 11 C． 20 ， 25 D ． 25 ， 20 7．如图，两个三角形的面积分别是 9 ， 6，对应阴影部分的面积分别是 m， n ，则 m﹣ n 等于（）） A． 2 B． 3 C． 4 D．无法确定 8．在 Rt △ABC 中， ∠ACB=90 ° ， AC=2 ，以点 B 为圆心， BC 的长为半径作弧，交 AB 于点 D，若点 D 为 AB 的中点，则阴影部分的面积是（） A． 2 ﹣ π B ． 4 ﹣ π C． 2 ﹣ π D ． π 9．如图，矩形 AB CD 与菱形 EFG H 的对角线均交于点 O，且 EG ∥ BC ，将矩形折叠，使点 C 与点 O 重合，折痕 MN 恰好过点 G 若 AB= ， EF=2 ， ∠ H=120 ° ，则 DN 的长为（）

A． B． C． ﹣ D． 2 ﹣ 10 ．已知二次函数 y=x 2+bx+ c 与 x 轴只有一个交点，且图象过 A（ x 1， m）、 B（ x 1+n ， m）两点，则 m、 n 的关系为（） A． m= n B． m= n C ． m= n 2D． m= n 2 二、填空题．（本大题共 6 小题，每小题 3 分，共 18 分） 11 ．若代数式 12 ．如图， AC 是正五边形 AB CDE 的一条对角线，则 ∠ ACB= 有意义，则 x 的取值范围是．． 13 ．已知关于 x 的方程 mx+3=4 的解为 x=1 ，则直线 y= （ m﹣ 2） x﹣ 3 一定不经过第象限． 14 ．如图，在 3 ×3 的方格中， A、 B 、 C、 D、 E、 F 分别位于格点上，从 C、 D、 E、 F 四点中任取一点，与点 A、B 为顶点作三角形，则所作三角形为等腰三角形的概率是． 15 ．设一列数中相邻的三个数依次为 m、 n、 p，且满足 p=m 2﹣ n，若这列数为 ﹣ 1， 3， ﹣ 2， a， ﹣ 7， b… ，则 b= 16 ．如图，在等腰直角 △ABC 中， ∠ ACB= 90 ° ， CO ⊥ AB 于点 O，点 D 、 E 分别在边 AC 、 BC 上，且 AD=CE ，连结 DE 交 CO 于点 P ，给出以下结论：． ①△ DO E 是等腰直角三角形；②∠ CDE= ∠COE ；③ 若 AC=1 ，则四边形 CEO D 的面积为；④ AD 2+BE 2 ﹣ 2OP 2=2DP •PE ，其中所有正确结论的序号是．

三、解答题．（本大题共 8 小题，共 72 分） 17 ．化简：（ 1+ ） ÷ ． 18 ．近几年来，国家对购买新能源汽车实行补助政策， 2016 年某省对新能源汽车中的 “ 插电式混合动力汽车 ” 实行每辆 3 万元的补助，小刘对该省 2016 年 “ 纯电动乘用车 ” 和 “ 插电式混合动力车 ” 的销售计划进行了研究，绘制出如图所示的两幅不完整的统计图．（ 1）补全条形统计图；（ 2）求出 “ D”所在扇形的圆心角的度数；（ 3）为进一步落实该政策，该省计划再补助 4.5 千万元用于推广上述两大类产品，请你预测，该省 16 年计划大约共销售 “ 插电式混合动力汽车 ” 多少辆？注： R 为纯电动续航行驶里程，图中 A 表示 “ 纯电动乘用车 ” ， B 表示 “ 纯电动乘用车 ” ， C 表示 “ 纯电动乘用车 ” （ R≥ 250km ）， D 为 “ 插电式混合动力汽车 ” ． 19 ．某大型企业为了保护环境，准备购买 A、 B 两种型号的污水处理设备共 8 台，用于同时治理不同成分的污水，若购买 A 型 2 台、 B 型 3 台需 54 万，购买 A 型 4 台、 B 型 2 台需 68 万元．（ 1）求出 A 型、 B 型污水处理设备的单价；（ 2）经核实，一台 A 型设备一个月可处理污水 220 吨，一台 B 型设备一个月可处理污水 190 吨，如果该企业每月的污水处理量不低于 1565 吨，请你为该企业设计一种最省钱的购买方案． 20 ．如图，在 ⊙ O 中，点 C 是直径 AB 延长线上一点，过点 C 作 ⊙ O 的切线，切点为 D，连结 BD ．（ 1）求证： ∠ A= ∠ BDC ；（ 2）若 CM 平分 ∠ ACD ，且分别交 AD 、 BD 于点 M、 N，当 DM=1 时，求 MN 的长．

21 ．如图，在平行四边形 ABCD 中，点 A、 B、 C 的坐标分别是（ 1， 0）、（ 3， 1 ）、（ 3， 3），双曲线 y= （ k≠ 0， x＞ 0）过点 D．（ 1）求双曲线的解析式；（ 2）作直线 AC 交 y 轴于点 E，连结 DE ，求 △ CDE 的面积． 22 ．如图， “ 中国海监 50 ” 正在南海海域 A 处巡逻，岛礁 B 上的中国海军发现点 A 在点 B 的正西方向上，岛礁 C 上的中国海军发现点 A 在点 C 的南偏东 30 ° 方向上，已知点 C 在点 B 的北偏西 60 ° 方向上，且 B 、 C 两地相距 120 海里．（ 1）求出此时点 A 到岛礁 C 的距离；（ 2）若 “ 中海监 50 ” 从 A 处沿 AC 方向向岛礁 C 驶去，当到达点 A′ 时，测得点 B 在 A′ 的南偏东 75 ° 的方向上，求此时 “中国海监 50 ”的航行距离．（注：结果保留根号） 23 ．在 Rt △ ABC 中，∠ C=9 0 ° ，Rt △ ABC 绕点 A 顺时针旋转到 Rt △ADE 的位置，点 E 在斜边 AB 上，连结 BD ，过点 D 作 DF ⊥ AC 于点 F．（ 1）如图 1，若点 F 与点 A 重合，求证： AC= BC ；（ 2）若 ∠DAF= ∠ DBA ， ① 如图 2，当点 F 在线段 CA 的延长线上时，判断线段 AF 与线段 BE 的数量关系，并说明理由； ② 当点 F 在线段 CA 上时，设 BE=x ，请用含 x 的代数式表示线段 AF ．

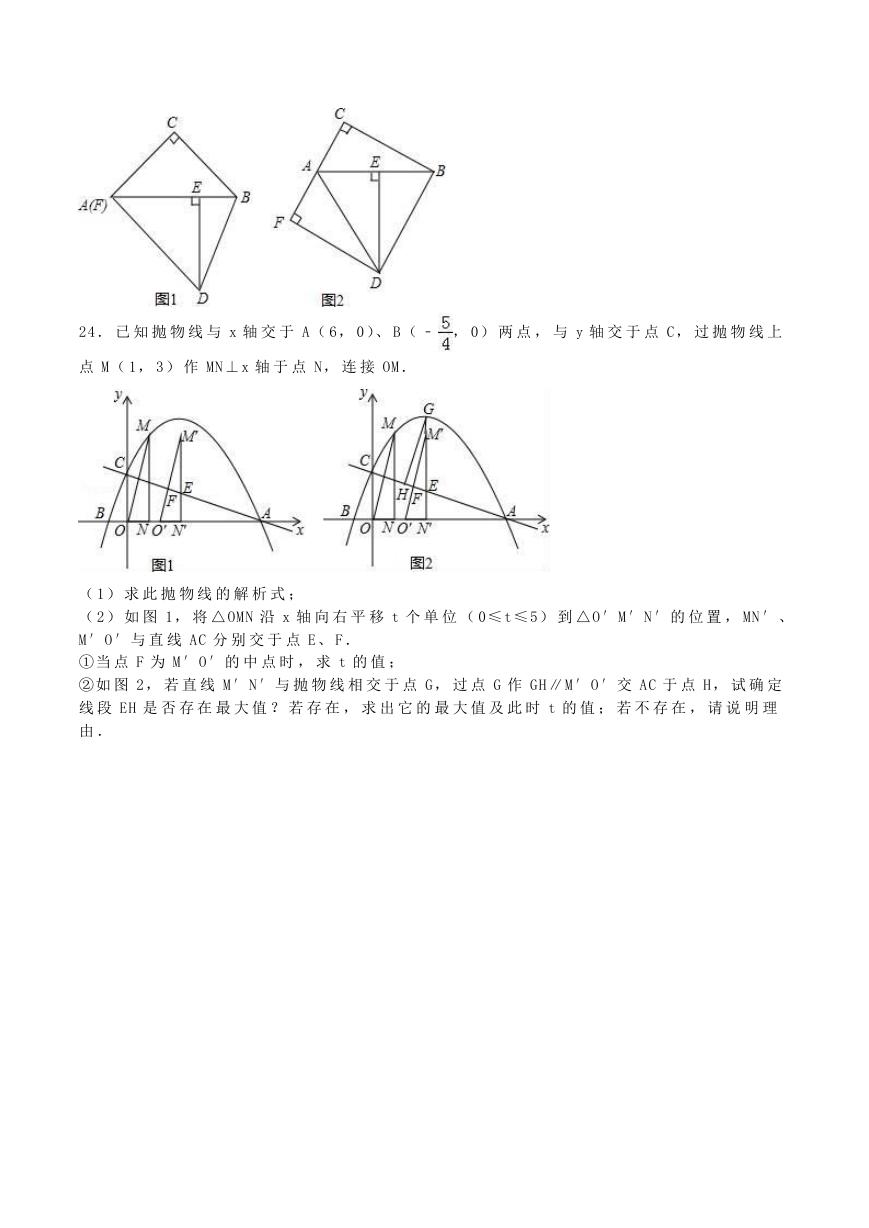
24 ．已知抛物线与 x 轴交于 A（ 6， 0）、 B（ ﹣ ， 0）两点，与 y 轴交于点 C，过抛物线上点 M（ 1， 3 ）作 MN ⊥ x 轴于点 N，连接 OM ．（ 1）求此抛物线的解析式；（ 2）如图 1，将 △ OMN 沿 x 轴向右平移 t 个单位（ 0≤ t≤ 5）到 △O′ M′ N′ 的位置， MN ′ 、 M′ O′ 与直线 AC 分别交于点 E、 F ． ① 当点 F 为 M′ O′ 的中点时，求 t 的值； ② 如图 2，若直线 M′ N′ 与抛物线相交于点 G，过点 G 作 GH ∥ M′ O′ 交 AC 于点 H，试确定线段 EH 是否存在最大值？若存在，求出它的最大值及此时 t 的值；若不存在，请说明理由．

201 6 年四川省资阳市中考数学试卷参考答案与试题解析一、选择题．（本大题共 10 小题，每小题 3 分，共 3 0 分） 1． ﹣ 2 的倒数是（） [来源 :学科网 ZX XK] A． ﹣ B． C． ﹣ 2 D． 2 【考点】倒数．【分析】根据倒数的定义即可求解．【解答】解： ﹣ 2 的倒数是 ﹣ ．故选： A ．） 2．下列运算正确的是（ A． x 4+x 2 =x 6B． x 2 •x 3=x 6 C．（ x 2） 3 =x 6D． x 2﹣ y 2=（ x﹣ y） 2 【考点】幂的乘方与积的乘方；合并同类项；同底数幂的乘法；因式分解 -运用公式法．【分析】根据合并同类项法则、同底数幂的乘法法则、积的乘方法则和公式法进行因式分解对各个选项进行判断即可．【解答】解： x 4 与 x 2 不是同类项，不能合并， A 错误； x 2•x 3 =x 5， B 错误；（ x 2） 3 =x 6， C 正确； x 2﹣ y 2 =（ x+y ）（ x ﹣ y）， D 错误，故选： C ． 3．如图是一个正方体纸盒的外表面展开图，则这个正方体是（） A． B． C． D．【考点】几何体的展开图．【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系，进而可得出结论．【解答】解： ∵ 由图可知，实心圆点与空心圆点一定在紧相邻的三个侧面上， ∴ C 符合题意．故选 C． 4．世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微小的无花果，质量只有 0.000000076 克，将数 0.000 000076 用科学记数法表示为（ A． 7.6 × 10 ﹣ 9B． 7.6 × 10 ﹣ 8C． 7.6 × 10 9D． 7.6 × 10 8 【考点】科学记数法 — 表示较小的数．）

【分析】绝对值小于 1 的正数也可以利用科学记数法表示，一般形式为 a× 10 ﹣ n ，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的 0 的个数所决定．【解答】解：将 0.000000076 用科学记数法表示为 7.6 × 10 ﹣ 8 ，故选： B ．的运算结果应在哪两个连续整数之间（）＜＜，即可解答． 5． A． 2 和 3 B． 3 和 4 C ． 4 和 5 D． 5 和 6 【考点】估算无理数的大小．【分析】根据无理数的大小比较方法得到【解答】解： ∵ 即 5＜＜ 6， ∴ 故选： D ．＜＜，的运算结果应在 5 和 6 两个连续整数之间． 6．我市某中学九年级（ 1）班开展 “阳光体育运动 ” ，决定自筹资金为班级购买体育器材，全班 50 名同学筹款情况如下表：筹款金额（元）人数 5 3 10 7 15 11 20 11 25 13 30 5 ）则该班同学筹款金额的众数和中位数分别是（ A． 11 ， 20 B． 25 ， 11 C． 20 ， 25 D ． 25 ， 20 【考点】众数；中位数．【分析】中位数是一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；众数是一组数据中出现次数最多的数据．【解答】解：在这一组数据中 25 元是出现次数最多的，故众数是 25 元；将这组数据已从小到大的顺序排列，处于中间位置的两个数是 20 、20 ，那么由中位数的定义可知，这组数据的中位数是 20 ；故选： D ． 7．如图，两个三角形的面积分别是 9， 6，对应阴影部分的面积分别是 m， n，则 m﹣ n 等于（） A． 2 B． 3 C． 4 D．无法确定【考点】三角形的面积．【分析】设空白出的面积为 x，根据题意列出关系式，相减即可求出 m﹣ n 的值．【解答】解：设空白出图形的面积为 x ，根据题意得： m+x=9 ， n+x=6 ，则 m﹣ n=9 ﹣ 6=3 ．故选 B．

8．在 Rt △ABC 中， ∠ACB=90 ° ， AC=2 ，以点 B 为圆心， BC 的长为半径作弧，交 AB 于点 D，若点 D 为 AB 的中点，则阴影部分的面积是（） A． 2 ﹣ π B ． 4 ﹣ π C． 2 ﹣ π D ． π 【考点】扇形面积的计算．【分析】根据点 D 为 AB 的中点可知 BC=BD= AB ，故可得出 ∠ A=30 ° ， ∠ B=6 0 ° ，再由锐角三角函数的定义求出 BC 的长，根据 S 阴影 =S △ A B C ﹣ S 扇形 C B D 即可得出结论．【解答】解： ∵ D 为 AB 的中点， ∴ BC= BD= AB ， ∴∠ A=30 ° ， ∠ B=6 0 ° ． ∵ AC= 2 ， ∴ BC= AC •tan30 ° =2 • =2 ， ∴ S 阴影 =S △ A B C ﹣ S 扇形 C B D = ×2 × 2﹣ =2 ﹣ π ．故选 A． 9．如图，矩形 AB CD 与菱形 EFG H 的对角线均交于点 O，且 EG ∥ BC ，将矩形折叠，使点 C 与点 O 重合，折痕 MN 恰好过点 G 若 AB= ， EF=2 ， ∠ H=120 ° ，则 DN 的长为（） A． B． C． ﹣ D． 2 ﹣ 【考点】矩形的性质；菱形的性质；翻折变换（折叠问题）．【分析】延长 EG 交 DC 于 P 点，连接 GC 、 FH ，则 △ GCP 为直角三角形，证明四边形 OGC M 为菱形，则可证 OC=OM=CM=OG= ，由勾股定理求得 GP 的值，再由梯形的中位线定理 CM+DN=2GP ，即可得出答案．【解答】解：长 EG 交 DC 于 P 点，连接 GC 、 FH ；如图所示：则 CP=DP= CD= ， △ GCP 为直角三角形， ∵ 四边形 EFGH 是菱形， ∠ EHG=120 ° ， ∴ GH= EF=2 ， ∠OHG=60 ° ， EG ⊥ FH ， ∴ OG= GH •sin60 ° =2 × = ，

资料库

2016年四川省资阳市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料