GeoStudio非饱和渗流关键问题探讨.pdf

发布时间：2022-06-01 发布人：admin 分类：说明书资料大小：0.78M 资料格式：pdf 举报版权申诉

hetianxun123-9193923-4744302543415791351.pdf-第1页.png

第1页 / 共47页

hetianxun123-9193923-4744302543415791351.pdf-第2页.png

第2页 / 共47页

hetianxun123-9193923-4744302543415791351.pdf-第3页.png

第3页 / 共47页

hetianxun123-9193923-4744302543415791351.pdf-第4页.png

第4页 / 共47页

hetianxun123-9193923-4744302543415791351.pdf-第5页.png

第5页 / 共47页

hetianxun123-9193923-4744302543415791351.pdf-第6页.png

第6页 / 共47页

hetianxun123-9193923-4744302543415791351.pdf-第7页.png

第7页 / 共47页

hetianxun123-9193923-4744302543415791351.pdf-第8页.png

第8页 / 共47页

文本预览

GeoStudio 软件使用体会交流 GeoStudio 软件使用体会交流汇报题目：非饱和渗流关键问题探讨罗红明中国科学院武汉岩土力学研究所 2010年年66月月 2010

汇报提纲汇报提纲汇报提纲一、非饱和土特性二、非饱和渗流基本理论三、非饱和数值求解关键问题四、降雨数值分析中几个问题五、应用实例分析

一、非饱和土特性 1、土水特征曲线基质吸力直接影响着非饱和土的力学性质。对于非饱和土体，其基质吸力的大小则是土体含水量的函数。非饱和土的基质吸力随着含水量的变化而变化，含水量和基质吸力的关系曲线称为土水特性曲线。土水特性曲线对于研究非饱和土的物理力学特性至关重要。根据土水特性曲线可以确定非饱和土的强度和渗透系数，甚至可以确定地下水面以上水分分布。因此，研究含水量对非饱和土力学性质的影响，就是研究非饱和土力学性质与基质吸力以及土水特性曲线的相互关系。土水特性曲线的研究，起源于土壤学和土壤物理学。当时主要着重于天然状态下表层土壤吸力的变化、土壤的持水特性及水分运动特征的研究，基质吸力值一般小于100kPa。近年来，由于非饱和土力学理论在斜坡稳定性评价以及降雨型滑坡预测等方面的广泛应用，对非饱和土的土水特性曲线进行了更加深入的研究。

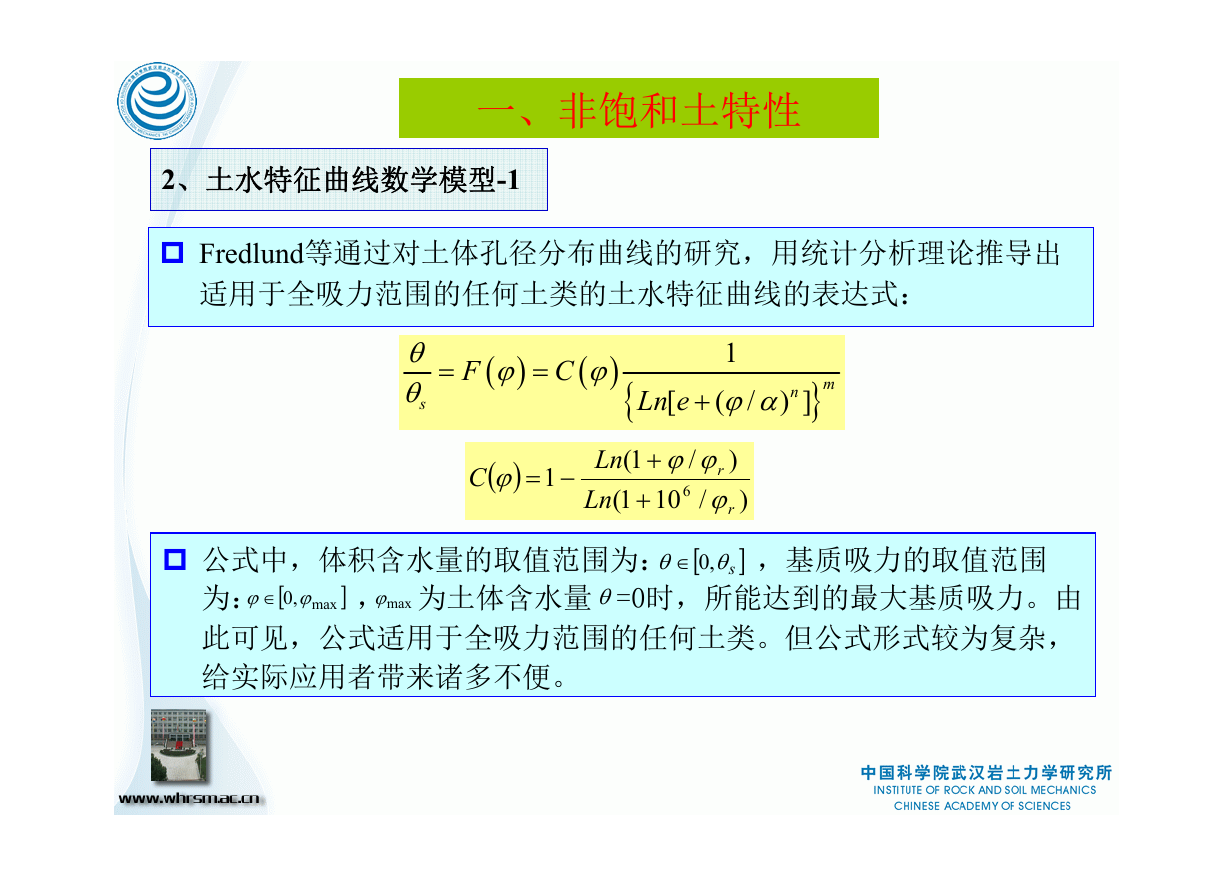
一、非饱和土特性 2、土水特征曲线数学模型-1 Fredlund等通过对土体孔径分布曲线的研究，用统计分析理论推导出适用于全吸力范围的任何土类的土水特征曲线的表达式： θ θ s = F ( ) ϕ = C C ( ) ϕ −= 1 1 ( ϕ α / n } ) ] m ( ) ϕ + Ln e [ { Ln 1( ) + ϕϕ r Ln 10 1( + ϕ r / 6 / ) 公式中，体积含水量的取值范围为： ]sθθ ,0∈ [ [ ]max maxϕ ,0 ϕϕ∈ ，为土体含水量 =0时，所能达到的最大基质吸力。由为：此可见，公式适用于全吸力范围的任何土类。但公式形式较为复杂，给实际应用者带来诸多不便。 θ ，基质吸力的取值范围

一、非饱和土特性 2、土水特征曲线数学模型-2 Van Genuchten通过对土水特征曲线的研究，得出非饱和土体含水量与基质吸力之间的幂函数形式的关系式： θ θ r θ θ r − − s = F ( ) ϕ = 1 [1 ( + ϕα ) ] n m α n m 式中：，，为拟合参数，其中公式中，体积含水量的取值范围为： m 1 1 = − ]s r θθθ n [ ,∈ ]s [ ,∈ 。公式适用与描述基质吸力变化范围为为 r θθθ 征曲线。，符号意义同前。，基质吸力的取值范围的土水特 ]rϕϕ ,0∈ [

一、非饱和土特性 2、土水特征曲线数学模型-3 土水特征曲线的分形模型基于土体质量分布具有分形特征，以及孔隙数目与孔径之间的具有分形关系的认识。依据分形孔隙数目与孔径之间关系和Young-Laplace方程得到分形模型的通用表达式： θθ r θθ s r − − F ( ) ϕ = = ⎛ ⎜⎜ ⎝ ϕ ϕ b ⎞ ⎟⎟ ⎠ vD 3− 公式中，体积含水量的取值范围为： ]s ，基质吸力的取值范围 r θθθ ( ,∈ [ ∈ )r b ϕϕϕ , )r b ϕϕϕ , 为特征曲线。实际上，公式也是一种幂函数形式的数学模型。。公式适用于描述基质吸力变化范围为 ∈ [ 的土水

一、非饱和土特性 2、土水特征曲线数学模型-4 包承纲等通过对非饱和土气相形态的研究和划分，认为在实际工程应用中，只有部分连通内部两种气相形态需要着重研究。对照Fredlund 等的土水特征曲线（Fredlund的公式），发现该曲线在进气值和残余含水量两个特征点之间近乎为一条直线。于是用对数方程来表征土水特征曲线，并将其简化为： θθ r θθ s r − − = F )( ϕ = lg ϕϕ r lg ϕϕ r b lg − lg − [ ]r b ϕϕϕ ∈ 公式中，体积含水量的取值范围为： ]s r θθθ ，基质吸力的取值范围的土水特为征曲线。上式较公式前面的几个数学模型大为简化，其精度能满足一般工程需求。。上式适用于描述基质吸力变化范围为 [ ,∈ , ]r b ϕϕϕ ∈ [ ,

一、非饱和土特性 2、土水特征曲线数学模型-5 比较上面已有的土水特征曲线数学模型不难发现，体积含水量都是基质吸力的函数，不妨考虑应用Taylor级数展开式将它们写成统一的模型，并推导出以基质吸力为变量的土水特征曲线通用表达式。由于上述四类数学模型的右项都是关于基质吸力的函数，可以写成： θ F = θ s ( )ϕ θθ r = θθ r s − − F ( )ϕ 黄润秋等将公式上述几种模型在处展开为Taylor级数： = F ( ϕ b ) θ θ s ( F ′+ ϕϕϕ b ) ( b − ) + F ) ( ′′ ϕ b !2 ( ϕϕ b − ) 2 +……+ F ) ( n )( ϕ b n ! ( ϕϕ b − ) n + Q n )( ϕ

分享到：

赞收藏

资料库

GeoStudio非饱和渗流关键问题探讨.pdf

相关推荐

行业

热门标签

最新资料