《信息论与编码》 第四章 信息率失真函数 习题答案 4.1 解： 依题意可知：失真矩阵： d  10 01       ，转移概率 ( | j abp i )  1        1     2 2 D 平均失真：   1 1 j   1(2/1   i ( , badabpap () ( ) | i i j i ) j 2/10)     2/11   1(2/11  0)    4.2 解： 依题意可知：失真矩阵： D min D max   i min  ( xp i D j 当 min D 0 ， i ) (min , yxd  i )  j min j ( min DR  R d     10   02   ， 02/102/1)   0 j ( , yxdxp () i i 102/122/1(2/112/102/1)      ) 舍去 j 因为没有失真，此时的转移概率为 P  )0(  XH ( bit log ) 12   01     10   2/1 max D 当 因为取的是第二列的 maxD 值，所以输出符号概率: ( max  DR ， 0 ) 此编码器的转移概率为 P     10   10  ( bp 1 )  ,0 ( bp 2 ,1)  a 1  , ab 2 2  b 2 , 因 4.3 解： D max  min D j  min j  i D 当 min   i 0 min D ( xp i ) (min , yxd i j ( min DR )  ， 因为没有失真，此时的转移概率为  0 11 4 3 4  00 R i i j j ) )0( () 1 4 XH 11 11 1 ( , ) yxdxp 4 4 4 10 10 10 4 4 4 ) log 4 2 bit   0001     0010     0100   1000   P   ( 4/3 max D 当 因为任何一列的 maxD 值均为 3/4，所以取输出符号概 ( max  DR ) ， 0 

)  0 ，即 a 1  , ab 1 2  , ab 3 1  , ab 1 4  b 1 因此编 率: ( bp 1 ,1)  ( bp 2 )  码器的转移概率为 P )  ,0 ,0 ( ( bp bp 4 3 0001     0001     0001   0001    4.4 解： 依题意可知：失真矩阵： D min D max   i min  ( xp i D j 当 min D 0 ， j i ) (min , yxd  i )  j min j ( min DR  R d     4/110 4/101  ，     02/102/1)  0 ( , yxdxp () i i ) j  (4/1)4/12/14/12/1min(     其它 2 个均为 )2/1 因为没有失真，此时的转移概率为 P  )0(  XH ( bit log 12 )   001     010   ， 4/1 max D ( max  DR ) 0 当 ( bp 因为取的是第三列的 maxD 值为 1/4，所以取输出符号概率: 1 100   100  因此编码器的转移概率为 , ab 3      b 3 a 1 P 即  2 )  ,0 ( bp 2 )  ,0 ( bp 3 )  3 ， 4.5 解： (1)依题意可知：失真矩阵： d  10 01       ，转移概率为： P  1 q    0     q 1 ( ( ypxp ) i | j , yxdx i () i ) j 1(10 p  01 p p ) 1(1  q p ) 1(  q 0)  n m D   1 1 i j   1( ) p q    D min (2) i ( xp i ) (min , yxd i j ) j 1(0  p p 0)  0 因为 ) (DR 是 D 的递减函数，所以 max( ( DR ))  ( DR min )  DHpH  ) ( ( min )  p log p 1(  p ) log( 1  p ) 当 0q 时可达到 ，此时 0D ( )) max( DR  min j  j i (3) D max  min D ( , yxdxp () i i ) j  p p 1 0 p ( 1 另一个  ，p 更大 ) 舍去 因为 ) (DR 是 D 的递减函数，所以 min( ( DR ))  ( DR max )  DHpH  ) ( ( max )  0 

当 1q 时可达到 min( DR ( )) ，此时 D  1 p D min   ( xp i ) (min , yxd i j j 02/102/1)   0 1    10  0   ，信源 u )(up    0 1   2/12/1        ， D j  min j  i ( , yxdxp () i i ) j  2/102/1min(   2/1,  )12/112/1,02/1    (图略，见课堂展示) 4.6 解： 依题意可知：失真矩阵： d     D max   min[ i min , 1  (1]1, 另二个 ， ) 舍去   D 0 因为二元等概信源率失真函数： )  ln ( DR DHn   a  ,2 1  a n  其中 ，所以率失真函数为：  1) ( DR D    4.7 解：失真矩阵为 110   101   011        d ，按照 P81 页方法求解（例 4-5 是二元输入和输入，本题是三元输入和输入， 超麻烦！明天再算好发送过来噢） 4.8 信息率失真函数 R(D)物理意义： ①R(D)是信源给定的情况下，在可容忍的失真度内再现信源消息所必须获得的最小平均信 息量； ②R(D)是反映给定信源可压缩的程度； ③R(D)求出后，就与选择的试验信道无关，而只是信源特性的参量，不同的信源，其 R(D) 是不同的。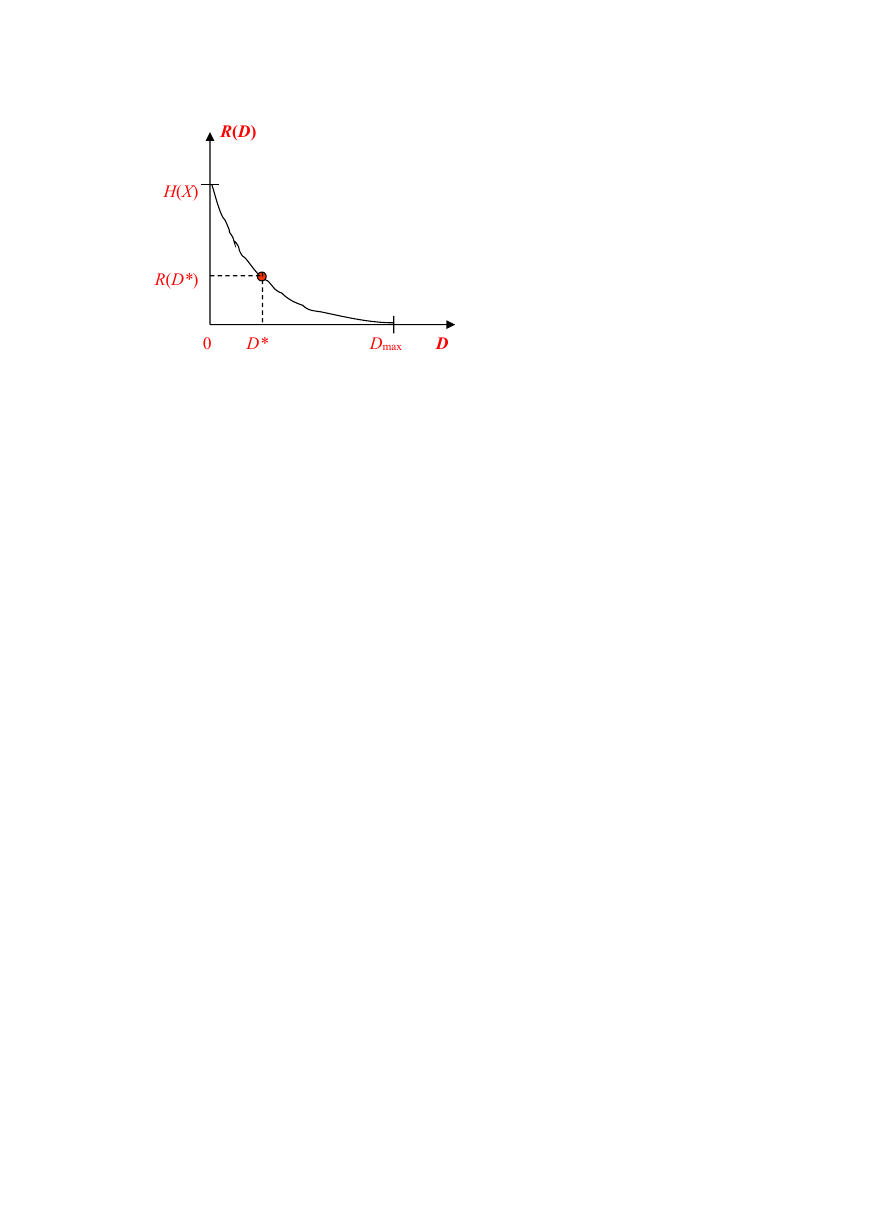 R(D)函数的性质： 性质 1 : R(D)在定义域内是下凸的 性质 2 : R(D)在定义域内是连续的 性质 3 : R(D)在定义域内是单调递减的 因此： 1. R(D)是非负函数，定义域 0～Dmax，值域 0～H(X)； 2. R(D)是单调不增、下凸的连续函数。 

R(D) H(X) R(D*) 0 D* Dmax D