logo资料库

论文研究-发现概率参数自适应调节的布谷鸟改进算法.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.71M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    16 2018，54（22） Computer Engineering and Applications 计算机工程与应用 发现概率参数自适应调节的布谷鸟改进算法 贾 涵，连晓峰 JIA Han, LIAN Xiaofeng 北京工商大学 计算机与信息工程学院，北京 100048 School of Computer and Information Engineering, Beijing Technology and Business University, Beijing 100048, China JIA Han, LIAN Xiaofeng. Improved cuckoo algorithm for adaptive adjustment of discovery probability parameter. Computer Engineering and Applications, 2018, 54（22）：16-22. Abstract：Cuckoo Search algorithm（CS）is a swarm intelligence optimization algorithm which is neoteric and inspired by biology. To overcome the defections that standard algorithm has slow convergence rate and the search for algorithm opti- mization ability is weak, a new Adaptive Probability of Cuckoo Search algorithm（APCS）is proposed. Firstly, a parameter called state discriminant Ps is proposed and calculated by using Pareto optimal solution. Secondly, an equilibrium param- eters Peb is created and calculated by exploration and exploitation equilibrium state. Finally, the adaptive dynamic adjust- ment of the discovery probability Pa is realized. In the end, eight benchmark functions are used to compare and analyze the performance of the two algorithms in 10 and 30 dimensions. Experiment results show that the convergence speed, opti- mization ability, stability and calculation time of APCS algorithm are better than those of CS algorithm. Key words：cuckoo search algorithm; convergence; dynamic parameters; global search; benchmarks 摘 要：布谷鸟搜索算法（CS）是一种受生物启发的新型群智能优化算法。针对 CS 算法在搜索后期收敛速度慢并且 寻优能力弱的问题，提出一种发现概率参数自适应调节的布谷鸟改进算法（APCS）。首先利用 Pareto 最优解计算出 状态判别参数 Ps ，其次通过探索-开发平衡状态计算出平衡参数 Peb ，最终实现鸟蛋的被发现概率 Pa 的自适应动态 调整。最后通过 8 个基准函数对两种算法的性能在 10 维和 30 维的情况下分别进行了对比与分析，结果表明，APCS 算法的收敛速度、寻优能力、稳定性和计算时间都优于 CS 算法。 关键词：布谷鸟搜索算法 ；收敛性 ；动态参数 ；全局搜索 ；基准测试 文献标志码：A 中图分类号：TP301.6 doi：10.3778/j.issn.1002-8331.1808-0057 1 前言 迄今为止优化算法分为传统优化算法和智能优化 算法。智能优化算法的理论研究主要包括算法的稳定 性分析、收敛性分析、收敛速度分析及算法的计算复杂 性分析等，这些研究中包含了对算法参数设置的一些理 论性指导。其中，关于稳定性的研究结果相对较多，但 收 敛 速 度 、收 敛 性 分 析 和 计 算 复 杂 性 的 研 究 相 对 较 少[1-2]。智能优化算法的应用研究覆盖了计算机、航空、 电力电子、电磁、地球物理、生物医学等大部分科技领域。 大量学者对常用优化算法进行改进研究，主要是通 过对参数的动态调节，参数的动态调节可分为适应性调 节、自适应性调节和非自适应调节三种基本类型。探索 与开发的权衡问题源于智能优化算法，主要是针对一些 基于种群的进化算法。探索-开发的权衡关系控制着算 法的计算代价和收敛质量，在保证算法的计算时间较短 的前提下，提高算法的收敛速度和寻优能力。改进算法 的主要思想是借助探索-开发的平衡关系来动态调节某 些相关参数。为了实现模态复杂问题的高效全局优化， 任何优化算法必须兼具“全局探索”和“局部开发”能力， 并在二者之间做出适当的权衡，有效的权衡有助于减少 计算代价和实现高效的优化。 元启发式群体智能算法是受“集体智慧”启发而提 基金项目：轨道交通控制与安全国家重点实验室（北京交通大学）开放课题基金项目（No.RCS2015K005）；2017 年北京工商大学两 科基金培育项目（No.LKJJ2017-23）。 作者简介：贾涵（1995—），女，硕士研究生，研究领域为人工智能，E-mail：13146500104@163.com；连晓峰（1977—），男，博士，副教 授，硕导，研究领域为复杂系统优化控制、机器视觉与图像处理、智能机器人。 收稿日期：2018-08-06 修回日期：2018-10-22 文章编号：1002-8331（2018）22-0016-07 计算机工程与应用www.ceaj.org
    贾 涵，等：发现概率参数自适应调节的布谷鸟改进算法 2018，54（22） 17 出的高效算法。集体智慧是通过环境中大量相同因子 的合作而出现的，例如鱼群、鸟群和蚂蚁群。在自然界 中，集体智慧通常被用于解决动物觅食，逃避追捕或生 存环境重新定位等问题。 群体智能优化算法主要受两个基本算法的启发： （1）蚁群算法，是受蚂蚁在寻找食物过程中发现路径的 行为启发；（2）粒子群优化算法，是受鸟群和鱼群的觅食 行为启发。群体智能“算法”或“策略”被认为是自适应 策略，并且通常应用于搜索和优化领域。常用的群体智 能优化算法有遗传算法（Genetic Algorithm，GA）、萤火 虫 算 法（Glowworm Swarm Optimization，GSO）、蚁 群 算法（Ant Colony Optimization，ACO）、人工蜂群算法 （Artificial Bee Colony algorithm，ABC）和粒子群优化 算法（Particle Swarm Optimization，PSO）等。 布谷鸟搜索算法（Cuckoo Search algorithm，CS）是 由英国牛津大学的 Yang 等学者提出的一种元启发式群 体智能算法[3-5]。该算法是在长期研究布谷鸟生活习性 的基础上提出的，主要利用了布谷鸟卵育寄生和莱维 （Lévy）飞行的特性，其优点是具有良好的适应性，参数 少，随机搜索路径优并且寻优能力强[6]。 该算法自提出以来得到了广泛的研究。在文献[7] 中 Yang 和 Rajabioun 等人将 CS 算法应用于工程优化和 多目标优化等实际问题中。文献[8-9]中 Walton 等人在 布谷鸟寻找鸟巢的时候引入了交换信息，但是由于对 CS 算法中的随机步长进行了改进，导致算法极易陷入 局部最优并且全局搜索能力过弱。在文献[10]中 Tuba 等学者对鸟巢的发现概率 Pa 和步长进行了动态自适应 的调整，提高了算法的收敛性能，但是由于算法完全依 赖随机游走，很难保证其搜索精度。在文献[11]中王凡 等学者在迭代过程中对鸟窝位置加入高斯扰动，提高了 CS 算法的收敛速度，但是由于引入了高斯算子，使算法 在搜索后期稳定性下降。在文献[12-13]中贺兴时等学 者通过分析鸟窝位置的群体状态转移过程，提高了算法 的全局搜索能力，但是由于加入 Markov 链，导致算法在 搜索后期收敛速度慢。文献[14-15]通过对种群的再分 组，并根据当前不同的搜索阶段对步长进行预先设置， 提高了 CS 算法的搜索性能，但是算法在转换搜索阶段 时增加了算法的计算时间并且存在很大的随机性。 从国内外的研究现状可以看出，CS 算法还有很大 的发展空间。但是 CS 算法也存在一些缺陷，比如在搜 索后期收敛速度慢，全局寻优能力弱，不稳定并且易陷 入局部最优，因此本文在深入分析 CS 算法的基础上，提 出了发现概率参数自适应调节的布谷鸟搜索算法（Adap- tive Probability of Cuckoo Search algorithm，APCS）。 首先设置一个状态判别参数 Ps 用来切换探索和开发的 状态，然后设置一个探索开发平衡参数 Peb 使探索和开 发阶段达到一个互补，最后实现了对发现概率 Pa 的动 态调整。实验结果表明了 APCS 算法较好地解决了 CS 算法后期存在的收敛速度慢、不稳定等缺点。 2 CS 算法的基本原理 布谷鸟搜索算法是模拟布谷鸟寻窝产卵的行为和 莱维飞行特性实现的元启发式群智能优化算法，其中布 谷鸟的卵育寄生行为和莱维飞行机制是算法的核心内容。 2.1 布谷鸟的卵育寄生行为 根据生物学家长期观察，布谷鸟的卵育寄生行为的 繁殖步骤如下[3-5]： 步骤 1 布谷鸟会在繁殖期寻找合适的宿主（大多为 雀形目鸟类）。 步骤 2 布谷鸟趁宿主外出时快速产蛋并将自己的 蛋放在宿主鸟巢里。 步骤 3 同时为了提高幼雏的成活率会移走一枚宿 主自己的蛋，使得巢中鸟蛋数量不变，在宿主不发现的 情况下代为孵化。 步骤 4 布谷鸟的蛋孵化时间短，通常最先孵出。之 后会将同巢的其余鸟蛋推出巢外，以至于得到更高的成 活率。 布谷鸟算法示意图如图 1。 布谷鸟 所有符合寄生条件的宿主的卵 布谷鸟的卵 布谷鸟随机选择的巢 布谷鸟雏鸟 布谷鸟以相同概率随机选择 布谷鸟推出宿主的一个卵 卵替换以后的巢 宿主孵化 独享宿主的哺育 图 1 布谷鸟算法示意图 2.2 布谷鸟的莱维飞行 以法国数学家保罗·莱维（Paul Lévy）命名的莱维 飞行机制具有较强的随机性，其步长服从幂律分布。这 是一种典型的随机游走过程，布谷鸟搜索算法使用的就 是这种飞行机制。当布谷鸟在寻找鸟巢时，其飞行就是 一种方向随机的运动，飞行轨迹和前一时刻的飞行轨迹 存在一定的偏差。布谷鸟飞行的过程主要以小步长为 主，但是偶尔有较大步长的位移，因此布谷鸟不会重复 停留在一个地方进行搜索[16-17]。 2.3 CS 算法的实现 在 CS 算法的具体实现中，首先提出以下三个理想 化的条件： （1）布谷鸟每次随机选择一个最优的鸟巢完成寄生； （2）孵化效果最好的鸟巢将会继续利用； （3）每次选择寄生的鸟巢数量是不变的，布谷鸟蛋 在宿主巢中被发现的概率为 Pa 。在这种情况下，宿主 可以抛出鸟蛋或者放弃当前鸟巢，并建一个新的巢。为 计算机工程与应用www.ceaj.org
    18 2018，54（22） Computer Engineering and Applications 计算机工程与应用 了方便研究和计算，这个理想化规则可以近似为被新巢 替换（新的随机解决方案）的概率为 Pa [18]。 i + α⊕L(λ),i = 1,2,⋯,n = x(t) i 表示第 i 个鸟巢在第 t + 1 代的位置；x(t) 在理想化的条件下，布谷鸟的位置更新公式如下： x(t + 1) （1） i 式中，x(t + 1) i 表 示第 i 个鸟巢在第 t 代的位置；α 表示比例步长因子，通 常 α = 1 ；L(λ) 代表随机搜索轨迹，随机步长服从以下 分布： Lévy~u = t-λ,1 < λ ≤ 3 式中，t 表示随机步长。 （2） 上述是布谷鸟卵育寄生行为、莱维飞行机制和布谷 鸟搜索算法的具体实现步骤。通过上述内容可以看出， 布谷鸟搜索算法具有参数少，对目标问题的初始状态 低，随机搜索路径优和寻优能力强等优点。 3 发现概率参数自适应调节的布谷鸟搜索算法 CS 算法在计算时比较繁琐，并且因为随机游走的 飞行机制导致相关性能会受到影响[19]。于是本文将基 本 CS 算法中的 Pa 由固定值调整为动态值，固定值将会 影响算法的全局搜索（探索）和局部搜索（开发）性能，并 且会导致算法收敛性能弱。 为此，本文提出一种发现概率参数自适应调节的布 谷鸟改进算法（APCS）。该算法的核心思想是通过协调 探索（全局）和开发（局部）的平衡关系，使参数 Pa 由固 定值变成自适应的动态参数，以提高算法的收敛性能和 寻优能力。 3.1 状态判别参数 若算法处在探索阶段的时候，局部搜索能力较弱， 容易陷入局部最优；若算法处在开发阶段的时候，全局 搜索能力较弱[20]。为了实现多目标问题的优化，任何优 化算法必须兼具“全局探索”和“局部开发”能力，并在二 者之间做出适当的权衡，才能使算法的性能达到最优。 APCS 算法将利用 Pareto 最优解，使探索和开发的性能 在一定程度上达到最好的状态，在全局搜索能力最优的 同时局部搜索能力也保持较优状态。从 Pareto 最优解 集中选择合适的解来作为探索-开发的判别标准[21-22]。 在可行性区域 Xf 中，对于 x ∈(0,1) ，不存在 x′ ∈ Xf ，使 得 F(x′) =( f1(x′),f2(x′),⋯,fk(x′)) 占 优 于 F(x) = ( f1(x),f2(x),⋯,fk(x)) ，则称 x 为 Xf 上的 Pareto 最优解。 APCS 算法的探索-开发模式如式（3）所示： Ps = nupdate nall （3） 式中，Ps 主要用于判断当前搜索过程处于探索阶段还 是开发阶段；nupdate 为更新的鸟巢数量；nall 为全部的鸟 巢数量。当 Ps < x 时，APCS 算法处于开发阶段，正在进 行局部搜索，此时算法极易陷入局部最优解，导致算法 的种群多样性下降，并且收敛性能不佳；当 Ps > x 时， APCS 算法处于探索阶段，正在进行全局搜索，此时虽然 算法保持了种群多样性，但是全局性太强并且易陷入局 部最优，使算法的性能不能达到最优状态。 3.2 探索开发平衡参数 探索（Exploration）是指在搜索优化过程中从整个 解空间范围内获取目标函数的信息，以便定位全局最优 解所在的局部区域。开发（Exploitation）是指在搜索优 化过程中对解空间中有希望包含最优解的局部区域进 行搜索，以便找到局部最优解甚至全局最优解的搜索策 略。通常将探索和开发分别视为全局搜索和局部搜索。 为了协调两个阶段的不足并发挥各阶段的优势，设 置参数 Peb 使探索和开发阶段达到一个互补状态，使 APCS 算法的收敛性能和寻优能力在兼具“全局探索”和 “局部开发”两个阶段下发挥出最好的性能，如式（4） 所示： 1 （4） 1 - Ps Peb = 当 Ps 较大时，算法处于探索阶段，那么为了提高算 法的开发能力，使得 Peb 为较小值；同理，当 Ps 较小时， 算法处于开发阶段，那么为了提高算法的全局搜索能 力，此时需要 Peb 为较大值。 3.3 发现概率参数 APCS 算法将发现概率 Pa 由一个固定值改成动态 值，主要通过对参数 Ps 和 Peb 的动态调整而提出用式（5） 实现算法参数 Pa 的自适应调整： Pa = 1 PebPs - exp é -æ êê èç ë i imax ù μλ úú û ö ø÷ （5） 其中，i 为当前迭代次数；imax 为最大迭代次数；μ 是在 区间 [0,1] 内均匀分布随机产生的实数；λ 为随机搜索 轨迹 (1 < λ ≤ 3) ； 1 表示当 Ps 的状态处于探索（开 发）阶段时，可以对开发（探索）的性能进行互补，达到一 种平衡状态。 PebPs 当 Ps > x 时，虽然计算时间短，但是收敛性能极差， 对算法进行 算法的全局搜索性能过强，因此通过 1 PebPs 改善。以全局搜索为主，局部搜索为辅，使探索阶段和 开发阶段保持平衡，最后求出使算法收敛性能和寻优能 力较好的动态 Pa 值。当 Ps < x 时，算法的局部搜索性 能过强，将会极易陷入局部最优。同理通过 1 对算 PebPs 法进行改善，进行局部搜索的同时也在进行全局搜索， 最终将会随着迭代的增加而达到全局最优和局部最优 的一种平衡。 APCS 算法将参数 Pa 由固定值调整成动态值，实现 了自适应的搜索策略，通过迭代次数的增加 Pa 的值也 计算机工程与应用www.ceaj.org
    贾 涵，等：发现概率参数自适应调节的布谷鸟改进算法 2018，54（22） 19 同时增大，使算法同时兼具探索性和开发性。算法的全 局搜索能力往往会随着迭代的进行而减弱，逐渐向局部 搜索转变，随着算法的逐渐收敛，多数解将集中到较小 的局部区域，最终使算法的各项性能得到提升。 3.4 算法实现 根据上述的条件，APCS 算法的具体实现步骤如下： 步骤 1 定义目标函数 f (x) ，并随机生成 nall 个鸟巢 的初始位置 xi(i = 1,2,⋯,nall) 。 步骤 2 计算每个鸟巢对应的目标函数，得到最优 值，并且利用位置更新公式对其余鸟巢的位置进行更新。 步骤 3 对比目前函数最优值，并作出相应改变。 步骤 4 计算参数 Ps 并与 Pareto 最优解求出的判别 标准 x 进行对比，若 Ps < x 时，处于开发阶段，反之则处 于探索阶段。 步骤 5 计算参数 Peb 实现对当前阶段性能的互补。 步骤 6 在位置更新后，用随机数 r ∈[0,1] 和更新后 i 进行改变，相反则 的 Pa 进行对比，若 r > Pa ，则对 x(t + 1) 保持不变。最后保留最好的一组鸟巢位置 y (t + 1) i 。 步骤 7 若未达到最大迭代次数或最小误差要求，则 返回步骤 2，否则，继续下一步。 APCS 算法的流程图如图 2 所示。 初始化目标函数 f (x) 初始化迭代次数 i = 0,最大迭 代次数 imax = 600,初始化种群， 计算所有初始解的适应值 通过位置更新公式对鸟巢位置进行更新 计算新解的适应值 通过 Ps 和 x 的关系 判断当前的搜索阶段 Ps > x Ps < x 处于开发阶段，并计算 Peb 处于探索阶段，并计算 Peb 通过计算 1 PebPs 处于探索阶段 使算法 通过计算 1 PebPs 处于探索阶段 使算法 部分劣解以发现概率 Pa 被丢弃并产生新解 较优的保留到下一代 找到并保存种群中的最优解 否 是否达到停止条件 是 结束 4 数值仿真与分析 通过仿真实验，测试上述改进算法的性能，并与 CS 算法的性能进行比较。仿真环境为 Windows 7 操作系 统，Intel 处理器，2.10 GHz，内存为 4 GB，仿真软件为 MATLAB 2014a。 4.1 测试函数 为了充分测试算法的性能和特点，选择 8 个标准函 数进行测试，其中涵盖了单模态和多模态函数，包括 Sphere、Shelter、Griewank 和 Rastrigin 等。各基准函数的 参数设置如表 2 所示，CS 算法和 APCS 算法分别进行 30 次独立实验，鸟巢 n = 30 ，最大迭代次数 imax 为 600，发 现概率 Pa 按式（10）进行动态调整，若收敛精度小于 1.00E－15 视为 0。 4.2 实验结果与分析 表 2 和表 3 分别记录了 APCS 算法和 CS 算法在 10 维 和 30 维的情况下，通过表 1 的 8 种测试函数得到的全局 最优值、最差值和平均值的相关实验数据，来对比两种 算法的收敛性能和全局寻优能力。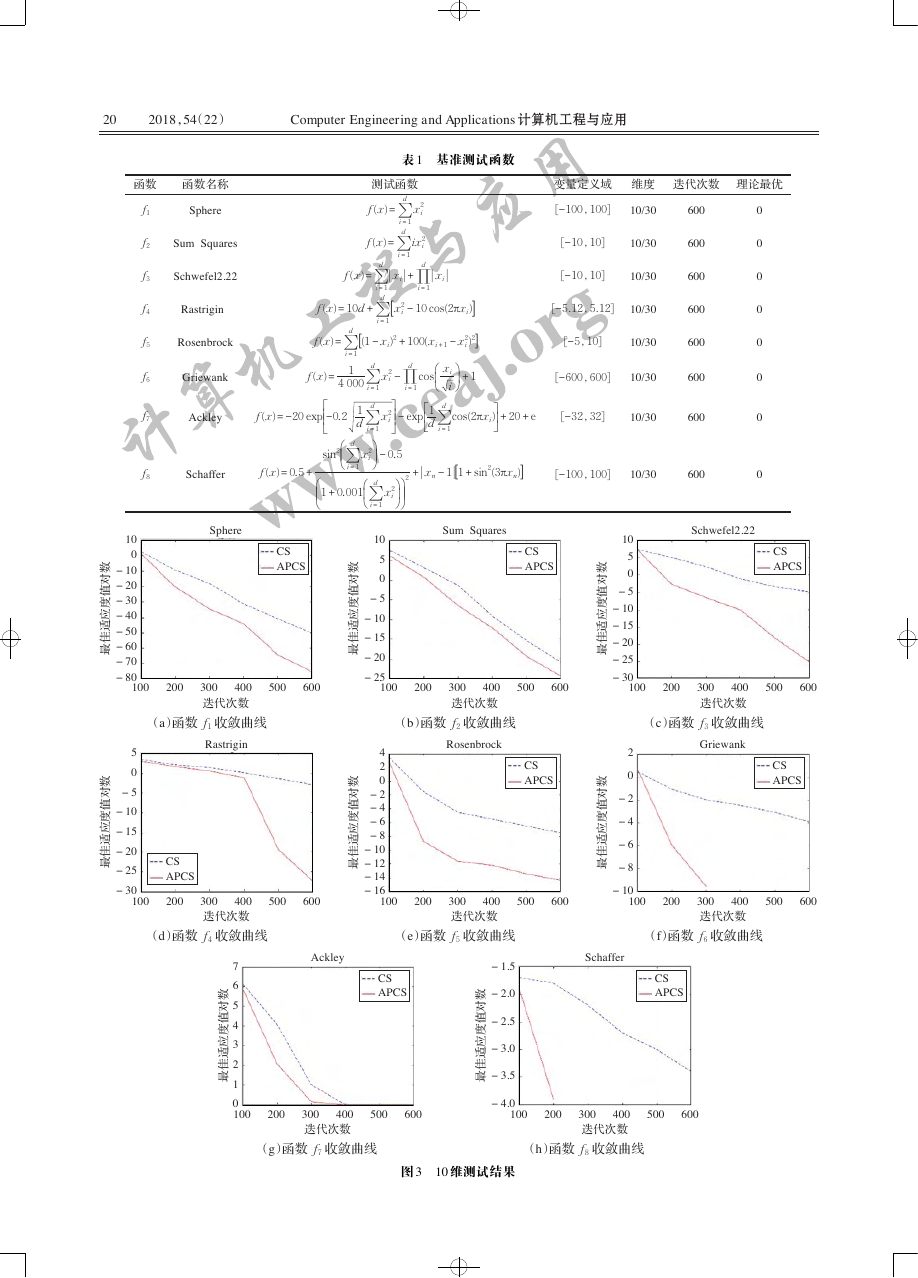 在 10 维的状态下实验结果如表 2 所示，最佳适应度 值随迭代次数变化的曲线如图 3 所示。 f1 和 f2 是一类简单的单峰且可分函数，这类函数 在整个搜索空间内只有一个峰值，APCS 算法分别比 CS 算法的最优值提高了 43 个和 28 个数量级，并且 APCS 基本接近了理论最优值。从图 3（a）和图 3（b）可以看出 APCS 算法的收敛性能优于 CS 算法，就稳定性而言，也 比 CS 算法更加稳定；f3 也是简单的单峰且可分函数， APCS 算法的最优值提高了 54 个数量级，在该基准函数 下，APCS 算法具有更强的收敛性；f4 和 f6 是一类复杂 的多峰、可分且高维的函数，并且这两个函数都是典型 的多模态非线性全局优化函数，整个搜索空间中存在多 个局部最优值，适用于衡量算法的寻优能力，并且使算 法的全局寻优能力和局部寻优能力保持平衡。随着迭 代次数的增加，APCS 算法可以更快地收敛，并且减少了 计算代价。在这两个基准函数的测试下，APCS 算法的 最优值、最差值和平均值均为 0，说明该算法的稳定性较 好；f5 和 f7 是一类复杂的多峰、不可分且高维的函数， 通过图 3（e）和图 3（g）可以看出，APCS 算法的收敛速度 明显优于 CS 算法，并且从表 2 的实验数据中可以看出 APCS 算法的最优值分别提高了 50 个和 65 个数量级，因 此较 CS 算法而言，其收敛精度和全局搜索能力得到了 较大的改善；f8 是一类复杂的多峰、不可分且低维的函 数，如图 3（h）所示，APCS 算法和 CS 算法皆避免了过早 收敛，但是 APCS 算法较 CS 算法在寻优能力上更能兼 顾全局搜索和局部搜索，使算法不易陷入局部最优又能 在较短时间内寻找到局部最优。 在 30 维的状态下实验结果如表 3 所示，最佳适应度 图 2 APCS 算法流程图 值随迭代次数变化的曲线如图 4 所示。 计算机工程与应用www.ceaj.org
    20 2018，54（22） Computer Engineering and Applications 计算机工程与应用 表 1 基准测试函数 f1 f2 f3 f4 f5 f6 f7 f8 10 0 －10 －20 －30 －40 －50 －60 －70 －80 100 数 对 值 度 应 适 佳 最 数 对 值 度 应 适 佳 最 | xi | ] x2 i - 10 cos(2πxi) i = 1 ] (1 - xi)2 + 100(xi + 1 - x2 i)2 测试函数 f (x) = ∑ d x2 f (x) = ∑ i = 1 i d i = 1 i = 1 i d i = 1 | d ix2 f (x) = ∑ | xi + ∏ d [ f (x) = 10d + ∑ f (x) = ∑ d [ i = 1 4 000∑ 1 d x2 ù é d ∑ i - expé -0.2 1 d x2 úú êê ê ë ë û i = 1 ÷÷∑ ö sin2æ d x2 i - 0.5 çç è ø ÷∑ ö d x2 ø 1 + 0.001æ ç è i - ∏ 2 ö ÷÷ ø æ çç è i = 1 i = 1 i = 1 i = 1 i f (x) = d cosæ ç è xi i d ∑ 1 d i = 1 + 1 ö ÷ ø cos(2πxi) + 20 + e ù ú û | xn - 1 [ | ] 1 + sin2(3πxn) + 变量定义域 维度 迭代次数 理论最优 [-100,100] 10/30 [-10,10] [-10,10] 10/30 10/30 [-5.12,5.12] 10/30 [-5,10] 10/30 [-600,600] 10/30 600 600 600 600 600 600 [-32,32] 10/30 600 [-100,100] 10/30 600 0 0 0 0 0 0 0 0 10 5 0 －5 －10 －15 －20 －25 100 Sum Squares CS APCS 200 300 400 迭代次数 500 600 （b）函数 f2 收敛曲线 Rosenbrock CS APCS 数 对 值 度 应 适 佳 最 数 对 值 度 应 适 佳 最 4 2 0 －2 －4 －6 －8 －10 －12 －14 －16 10 5 0 －5 －10 －15 －20 －25 －30 100 Schwefel2.22 CS APCS 200 300 400 迭代次数 500 600 （c）函数 f3 收敛曲线 Griewank CS APCS 2 0 －2 －4 －6 －8 数 对 值 度 应 适 佳 最 数 对 值 度 应 适 佳 最 100 200 400 300 迭代次数 500 600 －10 100 200 400 300 迭代次数 500 600 函数 函数名称 Sphere Sum Squares Schwefel2.22 Rastrigin Rosenbrock Griewank Ackley f (x) = -20 exp Schaffer f (x) = 0.5 + Sphere CS APCS 200 300 400 迭代次数 500 600 （a）函数 f1 收敛曲线 Rastrigin 5 0 －5 －10 －15 －20 －25 －30 100 CS APCS 200 400 300 迭代次数 500 600 （d）函数 f4 收敛曲线 （e）函数 f5 收敛曲线 （f）函数 f6 收敛曲线 7 6 5 4 3 2 1 数 对 值 度 应 适 佳 最 Ackley CS APCS －1.5 －2.0 －2.5 －3.0 －3.5 数 对 值 度 应 适 佳 最 Schaffer CS APCS 0 100 200 300 400 迭代次数 500 600 （g）函数 f7 收敛曲线 －4.0 100 200 300 400 迭代次数 500 600 （h）函数 f8 收敛曲线 图 3 10 维测试结果 计算机工程与应用www.ceaj.org
    贾 涵，等：发现概率参数自适应调节的布谷鸟改进算法 2018，54（22） 21 表 2 10 维实验结果分析 表 3 30 维实验结果分析 14 最优值 - - - Best 2.73E 0 3.41E 0 6.13E 0 6 28 3.00E+7 - - - - - - 0 4.40E 1.48E 3.32E 0 7.64E 8.04E 1.57E 0 16 61 15 20 76 14 Mean 平均值 - - - - - - 15 2.13E 57 5.72E 5 4.70E 39 6.65E 25 3.57E 72 4.63E 5.34E+8 0 - - 2.88E+16 2.15E 62 2.72E 14 0 - - 2.15E+15 7.68E 75 2.59E 16 0 基准函数 算法 Functions Algorithm f1 f2 f3 f4 f5 f6 f7 f8 CS APCS CS APCS CS APCS CS APCS CS APCS CS APCS CS APCS CS APCS 最差值 - - - - - - Worst 3 4.40E 14 2.42E 7 3.08E 15 1.28E 2 4.07E 16 3.26E 2.49E+2 0 - 7.89E+1 6.79E+1 4.12E 9 0 - - 5.22E+7 7.91E 15 3.63E 6 0 4 最优值 - - - Best 5.73E 0 4.19E 0 6.63E 0 6 2 3.56E+2 0 - - - - 6.29E+1 5.78E+1 3.78E 8 0 6.70E 8.04E 1.57E 0 13 19 7 平均值 - - - - - - Mean 5 2.89E 14 2.02E 5 5.78E 19 7.41E 3 1.43E 14 5.78E 4.89E+2 0 - 5.19E+1 4.23E+1 2.72E 10 0 - - 3.15E+8 7.89E 16 2.59E 9 0 Squares CS APCS 5 0 －5 －10 －15 数 对 值 度 应 适 佳 最 （b）函数 f2 收敛曲线 Rosenbrock CS APCS 数 对 值 度 应 适 佳 最 8 6 4 2 0 －2 －4 －6 －8 －10 100 Schwefel2.22 CS APCS 200 300 400 迭代次数 500 600 数 对 值 度 应 适 佳 最 1 0 －1 －2 －3 －4 －5 －6 100 （c）函数 f3 收敛曲线 Griewank CS APCS 200 400 300 迭代次数 500 600 （f）函数 f6 收敛曲线 Worst 最差值 - - - - - - 13 1.13E 56 2.91E 7 6.53E 35 5.99E 22 3.45E 76 1.32E 8.93E+7 0 - - 8.55E+15 1.27E 65 3.30E 12 0 - - 4.54E+13 8.88E 78 3.63E 12 0 CS APCS 基准函数 算法 Functions Algorithm f1 f2 f3 f4 f5 f6 f7 f8 CS APCS CS APCS CS APCS CS APCS CS APCS CS APCS CS APCS CS APCS Sphere 5 0 －5 －10 －15 数 对 值 度 应 适 佳 最 －20 100 200 300 400 迭代次数 500 600 －20 100 200 300 400 迭代次数 500 600 （a）函数 f1 收敛曲线 Rastrigin 5 数 对 值 度 应 适 佳 最 0 －5 －10 －15 －20 －25 －30 100 CS APCS 200 数 对 值 度 应 适 佳 最 400 300 迭代次数 500 600 4 2 0 －2 －4 －6 －8 －10 －12 －14 －16 （d）函数 f4 收敛曲线 （e）函数 f5 收敛曲线 100 200 400 300 迭代次数 500 600 Ackley CS APCS 7 6 5 4 3 2 1 数 对 值 度 应 适 佳 最 0 100 200 300 400 迭代次数 500 600 （g）函数 f7 收敛曲线 数 对 值 度 应 适 佳 最 －1.6 －1.8 －2.0 －2.2 －2.4 －2.6 －2.8 －3.0 100 Schaffer CS APCS 200 300 400 迭代次数 500 600 （h）函数 f8 收敛曲线 图 4 30 维测试结果 计算机工程与应用www.ceaj.org
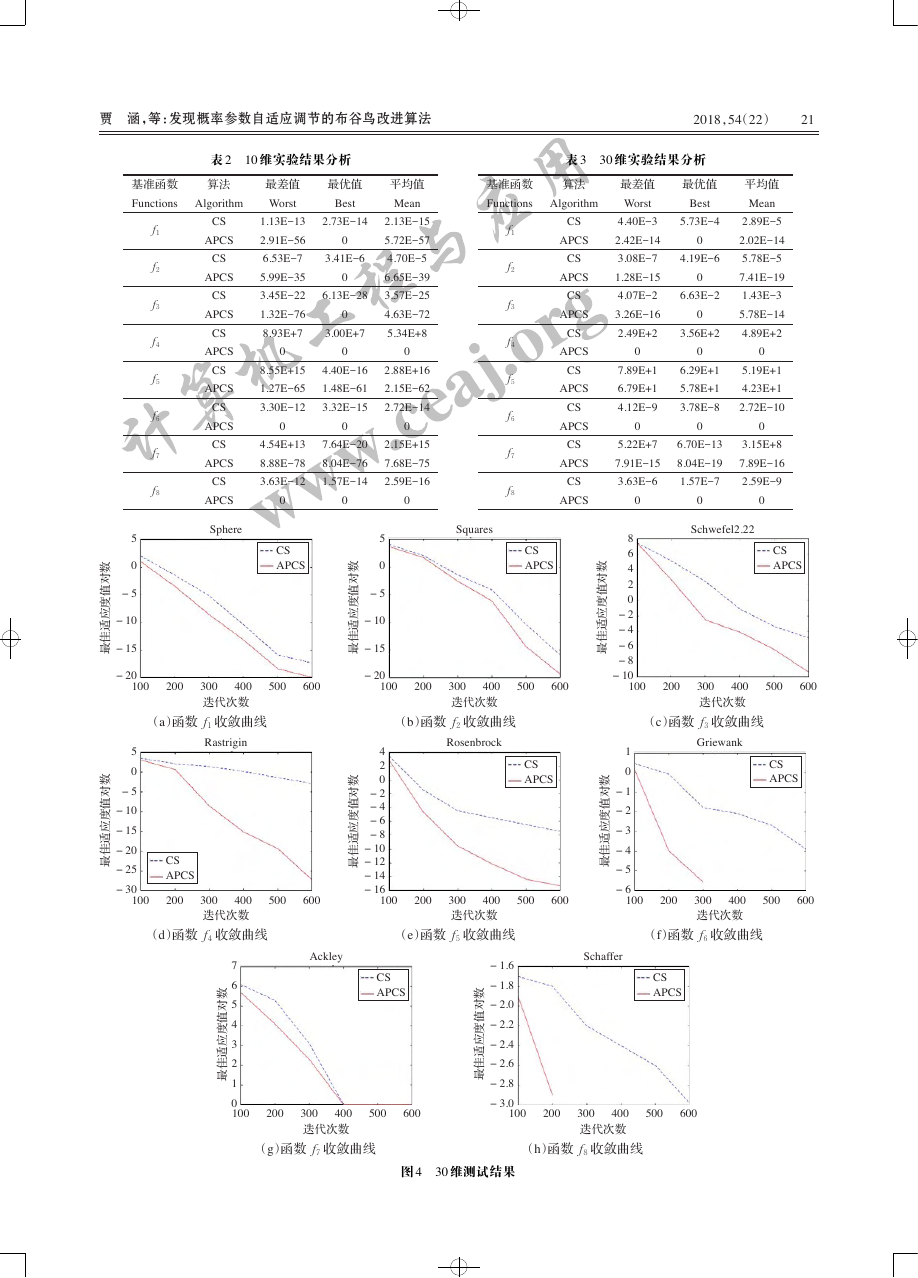
    22 2018，54（22） Computer Engineering and Applications 计算机工程与应用 表 3 列出了在 30 维情况下的测试结果，通过对比分 析 全 局 最 优 值 、最 差 值 和 平 均 值 的 实 验 数 据 验 证 了 APCS 算法的各项性能指标优于 CS 算法。对于 f1 、f2 和 f3 函数，APCS 算法的优化程度较 CS 算法的优化程 度虽然不是十分明显，但是收敛速度还是得到了改善， 并且通过表 3 的实验数据可以看出，APCS 算法具有更 好的全局搜索能力，同时又增强了局部搜索能力；f5 函 数是高维且多峰函数，不易找到全局最优解，但是通过 对概率的自适应调整以后，寻优能力得到了提高，并且 APCS 算法的收敛速度较快，同时节省了计算时间；f6 和 f8 在 30 维的情况下，APCS 算法的收敛速度远远高 于 CS 算法的收敛速度，并且迭代次数减少。 通过 8 个基准函数，对 APCS 算法和 CS 算法的各项 性能指标在 10 维和 30 维的状态下进行了对比分析。实 验数据和曲线图表明，APCS 算法的收敛速度、寻优能 力、稳定性和计算时间都优于 CS 算法，验证了算法的有 效性和改进后的优势。 5 结束语 本文在原始的 CS 算法基础上，着重研究了发现概 率参数自适应调节的布谷鸟改进算法。由于基本的 CS 算法在搜索后期存在收敛速度慢，寻优能力低，易陷入 局部最优并且不稳定等问题，通过对概率的自适应调整 加快了算法的收敛速度，提升了算法在兼顾全局搜索和 局部搜索时的寻优能力，并且在多峰函数下都不易陷入 局部最优。实验结果更一步验证了，APCS 算法的收敛 性能优并且相对稳定。从本文参考的文献中观察到， CS 算法及相关改进算法在医疗、图像处理、经济负荷调 度、工程设计和数据聚类等各个领域均有涉及，具有十 分广阔的研究前景。与其他算法相比，CS 算法的相关 参数少，并且易于与其他算法相融合，若能针对上述问 题展开深入研究，将会极大地促进该算法的发展，未来 将在理论分析方面对 CS 算法做进一步的研究。 参考文献： [1] Brownlee J.Clever algorithms：nature-inspired programming recipes[M].Lulu.com，2011. [2] Chen T.A simulative bionic intelligent optimization algo- rithm：artificial searching swarm algorithm and its perfor- mance analysis[C]//The 2nd International Joint Confer- ence on Computational Science and Optimization，2009： 864-866. [3] Yang X S，Deb S.Cuckoo search via Levy flights[C]//Pro- ceedings of World Congress on Nature & Biologically Inspired Computing.India：IEEE Publications，2009：210-214. [4] Yang X S，Deb S.Engineering optimization by cuckoo search[J].Int J Math Modeling & Num Optimization， 2010（4）：330-343. [5] Yang X S，Deb S.Multiobjective cuckoo search for design optimization[J].Computers & Operations Research，2013， 40（6）：1616-1624. [6] Srivastava P R，Khandelwal R，Khandelwal S，et al.Auto- mated test data generation using cuckoo search and tabu search（CSTS） algorithm[J].Journal of Intelligent Systems， 2012，21（2）：195-224. [7] Walton S，Hassan O，Morgan K，et al.Modified cuckoo search：a new gradient free optimisation algorithm[J].Chaos Solitons & Fractals，2011，44（9）：710-718. [8] Rajabioun R.Cuckoo optimization algorithm[J].Applied Soft Computing，2011，11：5508-5518. [9] Layeb A.A novel quantum inspired cuckoo search for knapsack problems[J].International Journal of Bio- Inspired Computation，2011，3（5）：297-305. [10] Tuba M，Subotic M，Stanarevic N.Modified cuckoo search algorithm for unconstrained optimization problems[C]// European Computing Conference.World Scientific and Engineering Academy and Society，2011：263-268. [11] 王凡，贺兴时，王燕 . 基于高斯扰动的布谷鸟搜索算法[J]. 西安工程大学学报，2011，25（4）：566-569. [12] 施文章，韩伟，戴睿闻 . 模拟退火下布谷鸟算法求解车间作 业调度问题[J].计算机工程与应用，2017，53（17）：249-253. [13] 王凡，贺兴时，王燕 . 基于 CS 算法的 Markov 模型及收敛 性分析[J]. 计算机工程，2012，38（11）：180-182. [14] Li X，Yin M.A particle swarm inspired cuckoo search algorithm for real parameter optimization[J].Soft Com- puting，2016，20（4）：1389-1413. [15] Liu X，Fu M.Cuckoo search algorithm based on frog leaping local search and chaos theory[J].Applied Math- ematics & Computation，2015，266（C）：1083-1092. [16] 周欢，李煜 . 具有动态惯性权重的布谷鸟搜索算法[J]. 智 能系统学报，2015（4）：645-651. [17] 范帅军 . 布谷鸟搜索算法的应用研究与改进[D]. 成都：西 南交通大学，2016. [18] 兰少峰，刘升 . 布谷鸟搜索算法研究综述[J]. 计算机工程 与设计，2015（4）：1063-1067. [19] 余方平，刘坚，马灿 . 汽车混流装配线的混合布谷鸟算法 排序研究[J]. 计算机工程与应用，2017，53（8）：240-245. [20] Dinh B H，Nguyen T T，Vo D N.Adaptive cuckoo search algorithm for short-term fixed-head hydrothermal sched- uling problem with reservoirvolume constraints[J].Grid Distrib Comput，2016，9（5）：191-204. [21] El Aziz M A，Hassanien A E.Modified cuckoo search algorithm with rough sets for feature selection[J].Neu- ral Computing and Applications，2018，29（4）：925-934. [22] Wang G G，Deb S，Gandomi A H，et al.Chaotic cuckoo- search[J].Soft Computing，2016，20（9）：3349-3362. 计算机工程与应用www.ceaj.org
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料