第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
基于多模型目标跟踪方法分析.doc
多 源 信 息 融 合
(仿真实验 1)
————基于多模型目标跟踪方法的仿真分析
姓名：王二小
班级：1431
学号：4114005073
专业：控制科学与工程
基于多模型目标跟踪方法的仿真分析
一.问题描述与数学模型:
在目标跟踪、故障检测、系统诊断等诸多信息融合领域，系统建模与真实模式间的失配
将导致融合结果退化。针对此类建模不确定问题，多模型方法(multiple-model methods, MM)
作为一类主流技术从理论和应用两方面都显示出有效性，长期以来成为相关领域的研究热点
之一。多模型方法自20世纪六七十年代被提出以来，迄今为止已经历了3代发展: 1) 静态多
模型方法(static MM, SMM)； 2) 交互式多模型方法(interactive MM, IMM)； 3)变结构多模型
方法(variable structure MM, VSMM)。 其中VSMM作为MM方法中的最新成果近几年来得到
了广泛关注。VSMM方法最早由李晓榕教授提出, 旨在解决IMM方法在面对系统大观测误差
或目标高度机动时所面临的困境—–为避免模型与真实模式间的失配,需引入更多的模型；但
过多的模型竞争反而可能导致估计结果退化；又增加了运算负担。本实验重点针对交互式多
模型进行仿真实验，以验证交互式多模型在目标跟踪中的准确性和有效性。
混合系统的一般模型如下：
x
k
)
F M x
k
(
j
1
G M u M
(
)
(
k
1
j
)
j
w M
k
1
(
)
j
j
,
1,
r
z
k
)
H M x
k
(
j
v M
k
1
(
)
j
j
1,
,
r
(1)
(2)
交互式多模型可以认为是在基本的状态空间中加入了模型参数，而该模型参数之间存在
一定的关系，其一次递推算法流程如下：
Step1：模型概率初始化 0 ，模型转移概率P以及状态初始值 0x 。
Step2：计算模型的混合概率
|
i j
1|
k
k
1
,
{
P M M z
|
j
k
1
i
k
k
1
}
1
c
j
(
,
P M M z
|
j
k
1
i
k
k
1
)
(
P M
i
k
1
|
z
k
1
)
(3)
该混合概率的实质是给定当前时刻的模型与前一时刻历史数据的条件下当前模型的概率。根
据模型的转移概率服从马尔科夫过程，则上式可改写为：
|
i j
1|
k
k
1
{
,
P M M z
|
j
k
1
i
k
k
1
}
1
c
j
P
ij
i
k
1
(4)
其中 jc 为归一化常数，表达式为：
c
j
r
1
i
p
ij
i
k
1
j
1,
，r为模型个数。
r
,
Step3：融合。根据前一时刻r个估计值，计算每个模型所对应的初始值状态，融合公式
如下：
x
0
k
j
1|
k
1
r
1
i
x
i
k
1|
k
1
|
i j
1|
k
k
1
j
1,
,
r
(5)
每个模型所对应的均方误差矩阵为：
x
j
1|
{
P
1
|
i j
1|
k
P
0
k
1
[
i
k
r
1
i
k
i
k
x
0
k
j
1|
] [
x
i
k
k
1
(6)
Step4：条件模型滤波。针对每一个初始值及初始协方差阵采用相对应的模型进行滤波，
1|
1|
1|
1
1
1
1
k
k
k
k
k
j
1,
]'}
,
r
x
0
k
j
1|
j
可以获得估计结果为 |
k kx 以及均方误差矩阵为 |
j
k kP 。每一个模型的似然函数为：
j
k
(
,
p z M z
|
j
k
k
k
1
)
(
,
p z M x
|
j
k
k
0
k
j
1|
k
,
1
0
P
k
j
1|
k
),
1
j
1,
,
r
该公式的实质是一个高斯的似然函数，其均值与协方差分别为：
z
|
k k
1
[
E z
k
|
z
k
1
]
j
H x
k
|
k k
1
H
j
k
0
{
F x
k
k
j
j
1|
k
1
j
G u
k
j
k
}
S
F
根据式(8)和式(9)可以获得基于模型的条件似然函数为：
H
|
k k
|
k k
1
1
1
k
)
j
k
j
k
0
{
F P
k
k
j
j
1|
(
E z
'
z
'
j
k
Q H
}
j
k
'
j
k
j
R
k
j
k
1(
2
j
kS
1_ [
2
) exp
z
z
j
k
| 1
k k
] (
S
j
k
)
1
[
z
j
k
z
| 1
k k
'
]
Step4：模型概率更新为：
j
k
(
|
P M z
j
k
k
)
(1 )
c
j
k
r
1
i
p
ij
i
k
1
j
1
r
(7)
(8)
(9)
(10)
(11)
其中
r
j
j
k
c
c
。
Step5：组合估计结果与协方差。将基于模型的估计结果与均方误差协方差矩阵进行组
1
j
合，其组合公式为：
x
|
k k
P
j
|
k k
r
j
1
{
P
j
|
k k
j
k
[
1
r
j
x
x
j
|
k k
j
|
k k
j
k
x
|
k k
x
j
|
k k
][
x
]'}
|
k k
(12)
(13)
组合过程只是针对于每个模型的估计结果进行组合，并不参与算法的过程中。
二.场景及模型集设置:
物体在运动过程中，不同时段的运动方式不同，所以只建立一个模型对目标的运动状态
进行估计不可能得到一个很好的估计结果，而采用多个模型在一定程度上能够克服单一模型
带来的这种弊端。为验证多模型的可靠性，采用如下场景：
场景(k)
1-30
31-45
46-55
56-80
81-98
99-119
120-139
140-150
151-160
表 1：目标的运动场景
ax(k)
0
18
2
0
25
-2
0
38
0
ay(k)
0
22
37
0
2
19
-1
-1
0
模型集的选择对估计准确与否至关重要，从主观来看，模型选择越多，正确模型落入所
选模型集的概率就越大，但是增加模型数会减慢模型集收敛到正确模型的速度，反而增加了
对正确模型的干扰，降低了估计的精度，所以模型集的选择依然是一个较为突出的问题。本
实验采用对称的二阶模型去估计目标的运动状态，其示意图 1 如下：
m1 : a=[0,0];
m4 : a=[-20,0];
m7 : a=[-20,20];
m10 : a=[40,0];
m13 : a=[0,-40];
m2 : a=[20,0];
m5 : a=[0,-20];
m8 : a=[-20,-20];
m11 : a=[0,40];
m3 : a=[0,20];
m5 : a=[20,20];
m9 : a=[20,-20];
m12 : a=[-40,0];
在交互式多模型中，设定状态转移矩阵，确定性输入矩阵以及系统噪声协方差矩阵为：
图 1.模型集合的选择
F
(
M
j
)
1,T,0,0;
0,1,0,0;
0,0,1,T;
0,0,0,1
G
(
M
j
)
/ 2,0,0,0;
/ 2,0;
2
T
0, T, 0, 0;
0,0,
0
, 0, 0, T;
T
2
Q
4
3
4
3
T
T
T
T
/ 4,
/ 2,
/ 4,
/ 2,
3
2
/ 2,
T
3
,
T T
/ 2,
T
3
,
T T
3
2
3
3
4
T
/ 2,
4
T
/ 2,
/ 4,
T
2
;
T
/ 4,
T
2
T
/ 2;
/ 2;
量测矩阵以及量测噪声的协方差矩阵为：
H M
(
j
)
1,0,0,0;
0,0,1,0;
R
_1
1,0;
0,1;
R
_ 2
10000,0;
0,10000;
从状态各模型的参数可以看出，模型间唯一不同在于模型的输入不同，各模型的输入如
图 1 所示。而量测模型给出了两个噪声协方差阵，显然前者的方差较小，称为小噪声模型，
而后者方差很大，称之为大噪声模型。然后设定模型的转移矩阵 P1，P1 的对角元素为 1/2，
其余元素为 1/24，设定模型初始概率为 为值为 1/13，模型的初始值 0
[0,1,0,0]
x
。
三．仿真结果：
仿真实验 1：验证噪声模型对估计结果的影响
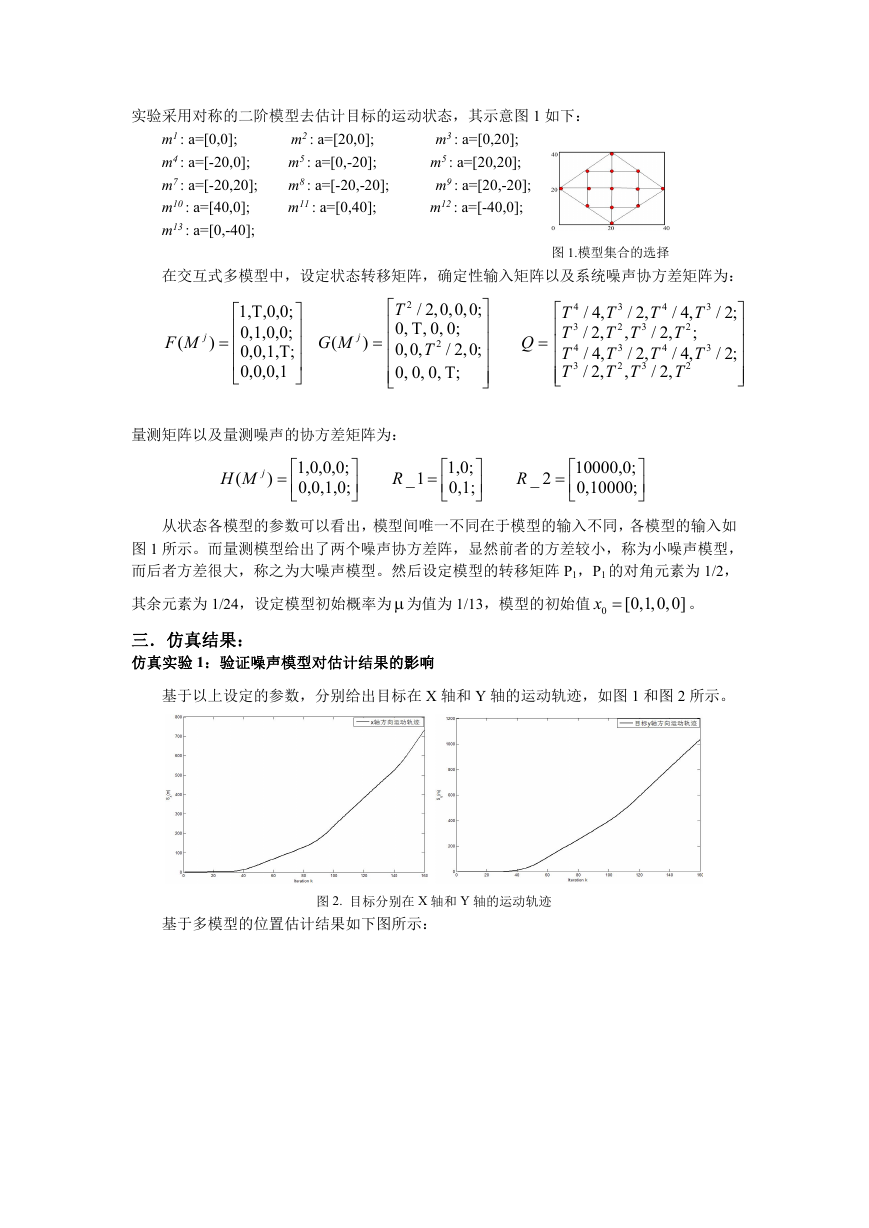
基于以上设定的参数，分别给出目标在 X 轴和 Y 轴的运动轨迹，如图 1 和图 2 所示。
基于多模型的位置估计结果如下图所示：
图 2. 目标分别在 X 轴和 Y 轴的运动轨迹
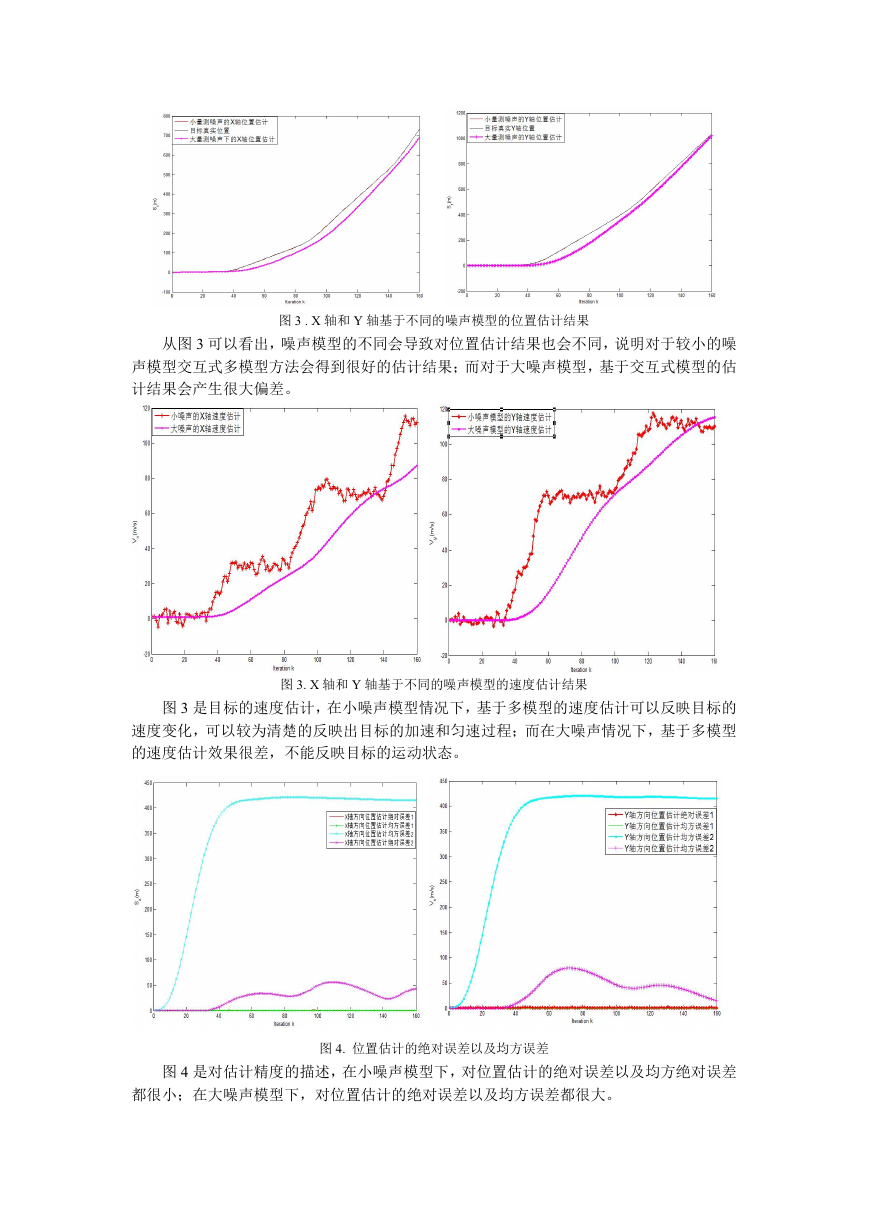
图 3 . X 轴和 Y 轴基于不同的噪声模型的位置估计结果
从图 3 可以看出，噪声模型的不同会导致对位置估计结果也会不同，说明对于较小的噪
声模型交互式多模型方法会得到很好的估计结果；而对于大噪声模型，基于交互式模型的估
计结果会产生很大偏差。
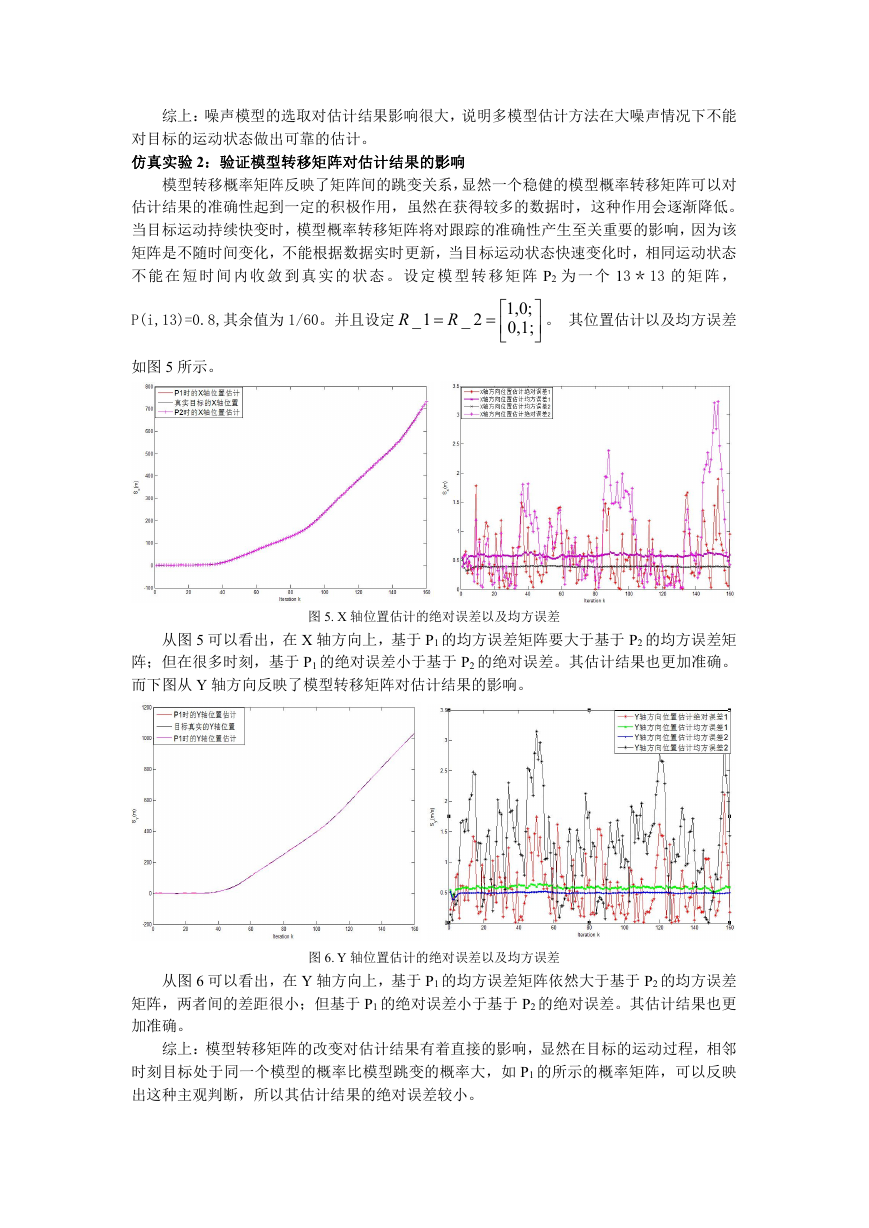
图 3. X 轴和 Y 轴基于不同的噪声模型的速度估计结果
图 3 是目标的速度估计，在小噪声模型情况下，基于多模型的速度估计可以反映目标的
速度变化，可以较为清楚的反映出目标的加速和匀速过程；而在大噪声情况下，基于多模型
的速度估计效果很差，不能反映目标的运动状态。
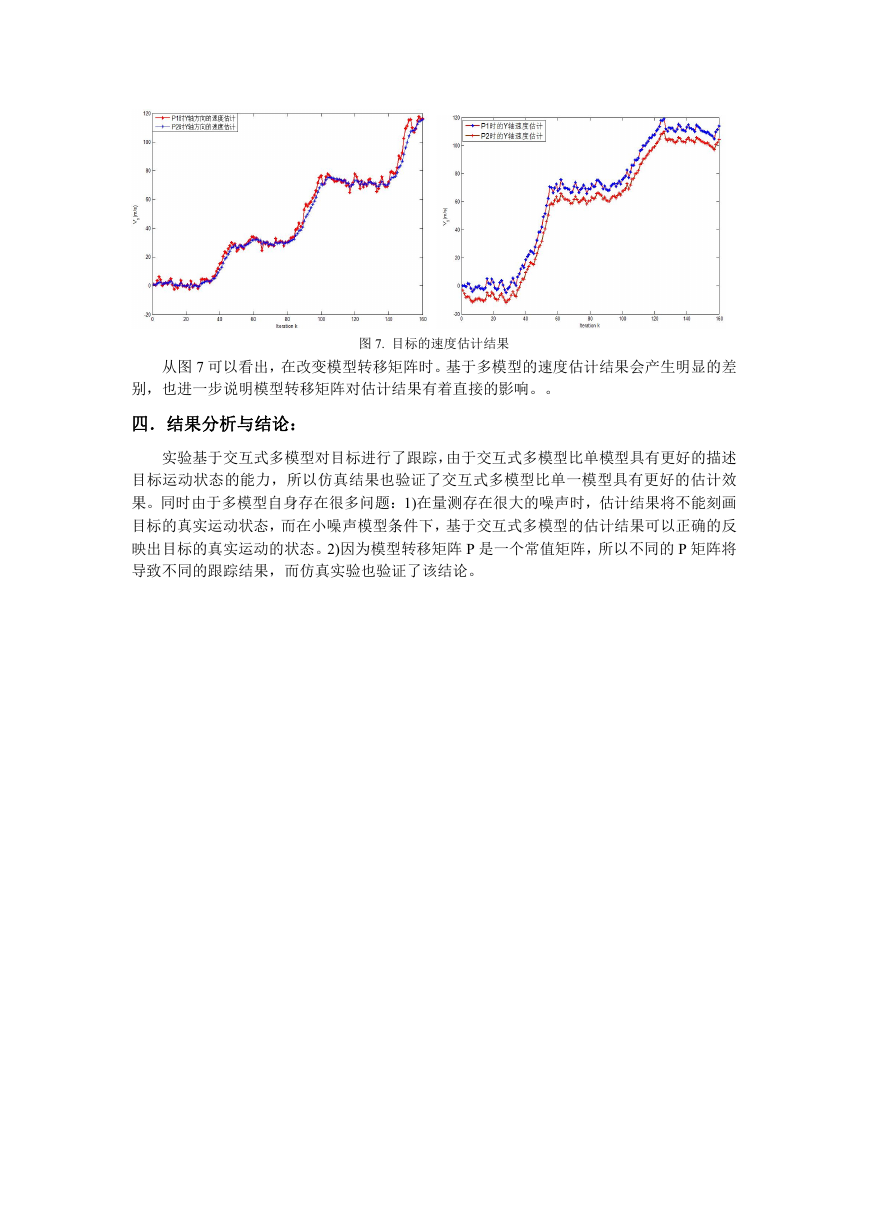
图 4. 位置估计的绝对误差以及均方误差
图 4 是对估计精度的描述，在小噪声模型下，对位置估计的绝对误差以及均方绝对误差
都很小；在大噪声模型下，对位置估计的绝对误差以及均方误差都很大。
综上：噪声模型的选取对估计结果影响很大，说明多模型估计方法在大噪声情况下不能
对目标的运动状态做出可靠的估计。
仿真实验 2：验证模型转移矩阵对估计结果的影响
模型转移概率矩阵反映了矩阵间的跳变关系，显然一个稳健的模型概率转移矩阵可以对
估计结果的准确性起到一定的积极作用，虽然在获得较多的数据时，这种作用会逐渐降低。
当目标运动持续快变时，模型概率转移矩阵将对跟踪的准确性产生至关重要的影响，因为该
矩阵是不随时间变化，不能根据数据实时更新，当目标运动状态快速变化时，相同运动状态
不 能 在 短 时 间 内 收 敛 到 真 实 的 状 态 。 设 定 模 型 转 移 矩 阵 P2 为 一 个 13 ＊ 13 的 矩 阵 ，
P(i,13)=0.8,其余值为 1/60。并且设定
R
_1
R
_ 2
1,0;
0,1;
。 其位置估计以及均方误差
如图 5 所示。
图 5. X 轴位置估计的绝对误差以及均方误差
从图 5 可以看出，在 X 轴方向上，基于 P1 的均方误差矩阵要大于基于 P2 的均方误差矩
阵；但在很多时刻，基于 P1 的绝对误差小于基于 P2 的绝对误差。其估计结果也更加准确。
而下图从 Y 轴方向反映了模型转移矩阵对估计结果的影响。
图 6. Y 轴位置估计的绝对误差以及均方误差
从图 6 可以看出，在 Y 轴方向上，基于 P1 的均方误差矩阵依然大于基于 P2 的均方误差
矩阵，两者间的差距很小；但基于 P1 的绝对误差小于基于 P2 的绝对误差。其估计结果也更
加准确。
综上：模型转移矩阵的改变对估计结果有着直接的影响，显然在目标的运动过程，相邻
时刻目标处于同一个模型的概率比模型跳变的概率大，如 P1 的所示的概率矩阵，可以反映
出这种主观判断，所以其估计结果的绝对误差较小。
从图 7 可以看出，在改变模型转移矩阵时。基于多模型的速度估计结果会产生明显的差
别，也进一步说明模型转移矩阵对估计结果有着直接的影响。。
图 7. 目标的速度估计结果
四．结果分析与结论：
实验基于交互式多模型对目标进行了跟踪，由于交互式多模型比单模型具有更好的描述
目标运动状态的能力，所以仿真结果也验证了交互式多模型比单一模型具有更好的估计效
果。同时由于多模型自身存在很多问题：1)在量测存在很大的噪声时，估计结果将不能刻画
目标的真实运动状态，而在小噪声模型条件下，基于交互式多模型的估计结果可以正确的反
映出目标的真实运动的状态。2)因为模型转移矩阵 P 是一个常值矩阵，所以不同的 P 矩阵将
导致不同的跟踪结果，而仿真实验也验证了该结论。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
