2020-2021 学年辽宁省营口市大石桥市八年级上学期期中数学试题及 答案 一、选择题（共 10 小题，每小题 3 分，共 30 分） 题号 1 答案 2 3 4 5 6 7 8 9 10 1.一个三角形的两边长分别为 3cm 和 7cm,则此三角形的第三边的长可能是( ) A 3cm B. 4cm C 7cm D 11cm 2.如图所示的标志中，是轴对称图形的有（ ）个。 A.1 B.2 C.3 D.4 3.一个多边形内角和是 1800°,从这个多边形的边数是（ ）。 A.8 B.10 C.12 D.18 4.如图,∠DBC、∠ECB 的平分线 BP、CP 交于点 P,则∠P 与 ∠A 的数量关系为( ) A.∠P=90°+∠A 1 2 C.∠P=90°+ ∠A B.∠P=90°-∠A 1 2 D.∠P=90°- ∠A 5.下列计算正确的是( ) A.  xy 3 3 xy B.  4 xy 22  16 2 x y 4 C. 2 xy 3  6 3 x y 3 D.   3 x 22  4 9 x 6.等腰三角形中，有一个角是 40°，它的一条腰上的高与底边的夹角是 A.20° B.50° C.25°或 40° D.20°或 50° 尺规作图作 AOB 77．．如图，如图，尺规作图作 以以O 为圆心，任意长为半径画弧交 为圆心，任意长为半径画弧交OA 、、OB 于于C 、、 D ，再分别以点 ，再分别以点 的平分线方法如下： 的平分线方法如下： C 、、 D 为圆心，以大于 为圆心，以大于 1 2 CD 长为半径画弧，两弧交于点 长为半径画弧，两弧交于点 P ，， 由作法得 OCP 作射线作射线OP，由作法得 BB、、SASSAS CC、、ASAASA AA、、SSSSSS △ ≌△ ODP DD、、AASAAS 的根据是（ 的根据是（ ））．． 88．．如图如图 44，已知，已知 AB AD ，那么那么 添加下列一个条件后， 添加下列一个条件后， ．．．． ABC △ 无法判定．．．． 仍仍无法判定 AA..CB CD CC.. BCA  ）） DAC  ∠ ∠ 90 D   ∠ ∠ 的是（的是（ BB.. BAC DD.. DCA ADC ≌△ ∠ ∠ B A O D B A C P 77 题题 D B 88 题题 C 99．．如图，如图，OPOP 平分平分∠∠AOBAOB，，PAPA⊥⊥OAOA，，PBPB⊥⊥OBOB，垂足，垂足 99 题题 分别为分别为 AA，，BB．下列结论中 ．下列结论中不一定成立的是 不一定成立的是（（ ））．． A.PA=PB A.PA=PB B.PO 平分平分∠∠APBAPB B.PO C.OA=OB C.OA=OB D.AB 垂直平分 D.AB 垂直平分 OPOP 

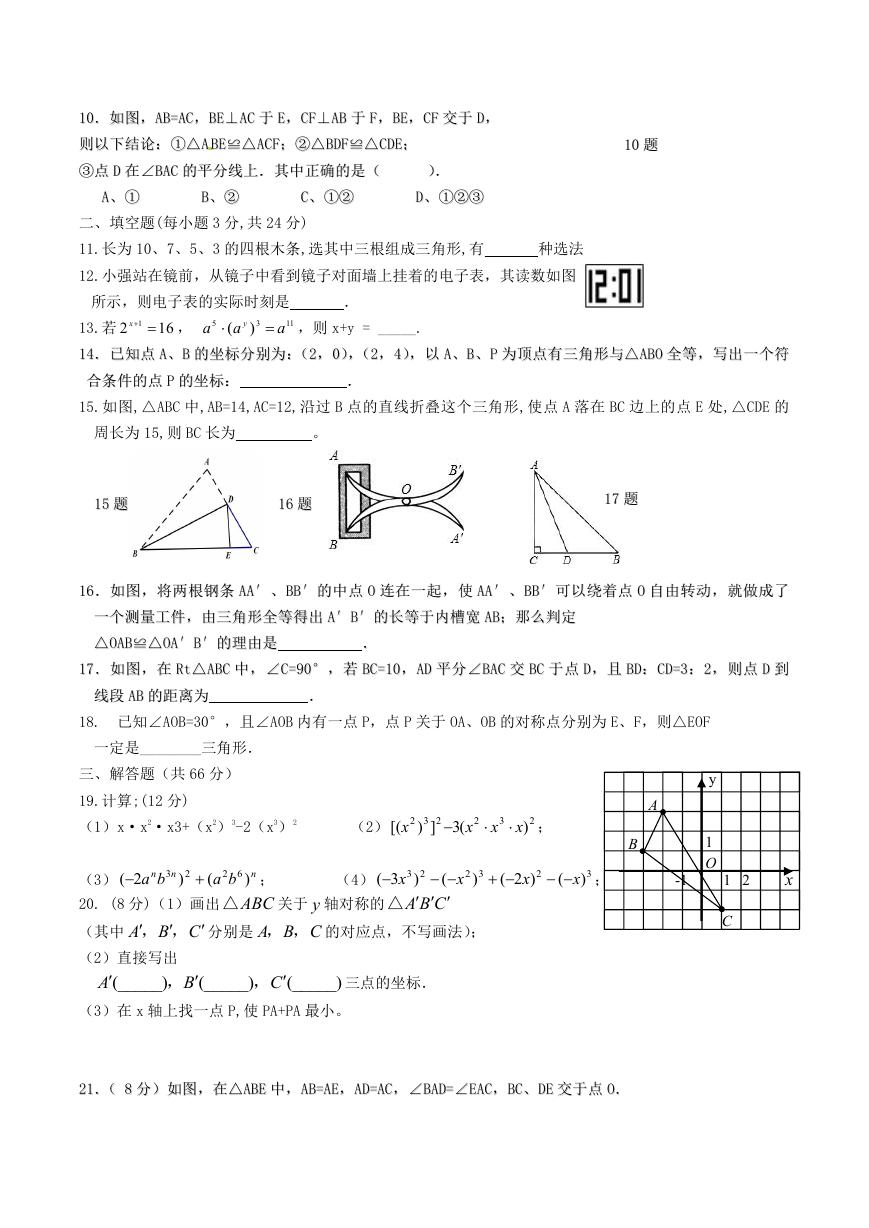
1010．如图， ．如图，AB=AC AB=AC，，BEBE⊥⊥ACAC 于于 EE，，CFCF⊥⊥ABAB 于于 FF，，BEBE，，CFCF 交于交于 DD，， 则以下结论：①△①△AA BEBE≌△≌△ACFACF；；②△②△BDFBDF≌△≌△CDECDE；； 则以下结论： 1010 题题 ③③点点 DD 在在∠∠BACBAC 的平分线上．其中正确的是 的平分线上．其中正确的是（（ ））．． AA、、①① BB、、②② CC、、①②①② DD、、①②③①②③ 二、填空题(每小题 3 分,共 24 分) 11.长为 10、7、5、3 的四根木条,选其中三根组成三角形,有 种选法 12.小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图 13.若 所示，则电子表的实际时刻是 a 1414．．已知点已知点 AA、、BB 的坐标分别为 2 1 x 16 ， ) (  5 ． y 3 11 a  a 的坐标分别为：：（（22，，00）），，（（22，，44）），以，以 AA、、BB、、PP 为顶点有三角形与 ，则 x+y = _____. 为顶点有三角形与△△ABOABO 全等，写出一个符 全等，写出一个符 合条件的点 PP 的坐标： 的坐标： 合条件的点 ．． 15.如图,△ABC 中,AB=14,AC=12,沿过 B 点的直线折叠这个三角形,使点 A 落在 BC 边上的点 E 处,△CDE 的 周长为 15,则 BC 长为 。 1515 题题 1616 题题 1717 题题 1616．．如图，将两根钢条 如图，将两根钢条 AAAA′′、、BBBB′′的中点的中点 OO 连在一起，使 连在一起，使 AAAA′′、、BBBB′′可以绕着点 可以绕着点 OO 自由转动，就做成了 自由转动，就做成了 一个测量工件，由三角形全等得出 AA′′BB′′的长等于内槽宽 一个测量工件，由三角形全等得出 的长等于内槽宽 ABAB；那么判定 ；那么判定 △△OABOAB≌△≌△OAOA′′BB′′的理由是 的理由是 ．． 1717．．如图，在 如图，在 RtRt△△ABCABC 中，中，∠∠C=90 C=90°°，若，若 BC=10 BC=10，，ADAD 平分平分∠∠BACBAC 交交 BCBC 于点于点 DD，且，且 BDBD：：CD=3 CD=3：：22，则点，则点 DD 到到 线段线段 ABAB 的距离为 的距离为 ．． 18. 已知∠AOB=30°，且∠AOB 内有一点 P，点 P 关于 OA、OB 的对称点分别为 E、F，则△EOF 一定是________三角形． 三、解答题（共 66 分） 19.计算;(12 分) （1）x·x2·x3+（x2）3-2（x3）2 （2） [( x 232 ]) (3  x 2 3  x 2  x ) ； A B （4） (  关于 y 轴对称的 A B C   23 )3( x  △ x 32 )  )2( x 2 (  x ) 3 ； -1  ， ， 分别是 A B C， ， 的对应点，不写画法）； 3 n 2 ) ( 62 ba ) n  2(  n ba （3） ； 20. (8 分)（1）画出 ABC△  （其中 A B C （2）直接写出  (_____) A B ，   (_____) （3）在 x 轴上找一点 P,使 PA+PA 最小。  (_____) C ， 三点的坐标． y 1 O 1 2 x C 2121．．（（ 88 分）如图，在 分）如图，在△△ABEABE 中，中，AB=AE AB=AE，，AD=AC AD=AC，，∠∠BAD= BAD=∠∠EACEAC，，BCBC、、DEDE 交于点交于点 OO．． 

求证求证：：（（11））△△ABCABC≌△≌△AEDAED；；（（22））OB=OE OB=OE．． 22. (8 分)如图所示，有一块三角形田地，AB=AC=10m，作 AB 的垂直平分线 ED 交 AC 于 D，交 AB 于 E，量 得△BDC 的周长为 17m，请你替测量人员计算 BC 的长. 23.完成下列各题（8 分） a 9 （1）已知 a （2）已知 m  ，求 a 的值 8 3 2 3, a n  求 2m n a  的值为多少. 4, 2244．．（（1010 分）如图，在 分）如图，在△△ABCABC 中，中，∠∠ACB=90 ACB=90°°，，ACAC =BC=BC，，BEBE⊥⊥CECE 于点于点 EE．．ADAD⊥⊥CECE 于点于点 DD．． 求求 证：证：(1)(1)△△BECBEC≌△≌△CDACDA．．(2)AD-BE=DE (2)AD-BE=DE 八年数学（2020、11）第 3 页 共 4 页 八年数学（2020、11）第 4 页 共 4 页 

25.(12 分)如图,在 Rt△ABC 中,∠ABC=90°,BC=2AB,点 D 是 BC 的中点,将一块锐角都为 45°的等腰直角三 角板 BED 如图放置,使三角板斜边的两个端点分别与 B、D 重合,点 E 为直角三角板的直角顶点,连接 AE、 EC.试猜想线段 AE 和 EC 的数量及位置关系,并证明你的猜想 八年数学参考答案 一、CCCDB DACDD 二、11.2 12.10:21 13.5 14.（4,0）（0.8）15.15 16.SAS 17.4 18. 等边 三、19.（1）0 （2）-2x12 （3）5a2nb6n（4）10x6+x3+4x2 20.（1）略 （2）（2,2） （3,0）（-1，-2）(3)略 21. （（11）利用）利用 SASSAS 可证明可证明 △△ABCABC≌△≌△AEDAED。。 （（22））∵△∵△ABCABC≌△≌△AEDAED∴∠∴∠ABC= ABC=∠∠AEDAED ∵∵AB=AE AB=AE ∴∠∴∠ABE= ABE=∠∠AEBAEB ∴∠∴∠OBE= OBE=∠∠OEBOEB ∴∴OB=OE OB=OE 22.17 23.（1）2 （2）36 24.（1）∵∠∵∠ACD+ ACD+∠∠BCE=90 BCE=90°°,, ∠∠ACD+ ACD+∠∠DAC=90 DAC=90°∴∠°∴∠BCE= BCE=∠∠DACDAC ∵∠∵∠BEC= BEC=∠∠ADC=90 ADC=90°∴△°∴△BECBEC≌△≌△CDACDA 

(2)(2) ∵△∵△BECBEC≌△≌△CDACDA ∴∴CE=AD,BE=CD CE=AD,BE=CD ∵∵CE-CD=DE CE-CD=DE ∴∴AD-BE=DE AD-BE=DE 25.垂直且相等 证明证明 △△ABEABE≌△≌△CDECDE 即可。即可。