数据结构与算法(吴跃)-课后习题参考答案.pdf

发布时间：2022-06-13 发布人：admin 分类：说明书资料大小：1.65M 资料格式：pdf 举报版权申诉

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第1页.png

第1页 / 共25页

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第2页.png

第2页 / 共25页

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第3页.png

第3页 / 共25页

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第4页.png

第4页 / 共25页

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第5页.png

第5页 / 共25页

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第6页.png

第6页 / 共25页

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第7页.png

第7页 / 共25页

470cb64f-0e33-466d-9c92-f8ec33e481c7.pdf-第8页.png

第8页 / 共25页

文本预览

习题答案第１章参考答案一、填空题１．数据元素的有限集，犇中数据元素之间客观存在的关系的有限集２．顺序存储结构，链式存储结构，散列存储结构３．犗（犿狀）４．犗（狀）５．犗（ｌｏｇ３狀）二、选择题１．Ｃ　　２．Ｄ　　３．Ｂ　　４．Ｃ，Ａ　　５．Ｃ三、简答题１．数据结构就是带有结构的数据的集合，包括数据元素、元素之间的关系和对数据元素的操作３个部分；逻辑结构包括线性表、栈、队列、树、二叉树、无向图、有向图等，结构特征即元素之间的关系。２．５个特点：１）有穷性；２）确定性；３）可行性；４）输入；５）输出。２个区别：１）有穷性；２）描述方法。３．设犳犪犮狋（狀）的运行时间函数是犜（狀）。该函数中语句①的运行时间是犗（１），语句②的运行时间是犜（狀－１）＋犗（１），其中犗（１）为运行时间。因此：则：犜（狀）＝犗（１）　　　　　　　狀≤１犜（狀－１）＋犗（１）　　狀＞１｛犜（狀）＝犗（１）＋犜（狀－１）　　　　　＝２犗（１）＋犜（狀－２） … ＝（狀－１）犗（１）＋犜（１）＝狀犗（１）＝犗（狀）即犳犪犮狋（狀）的时间复杂度为犗（狀）。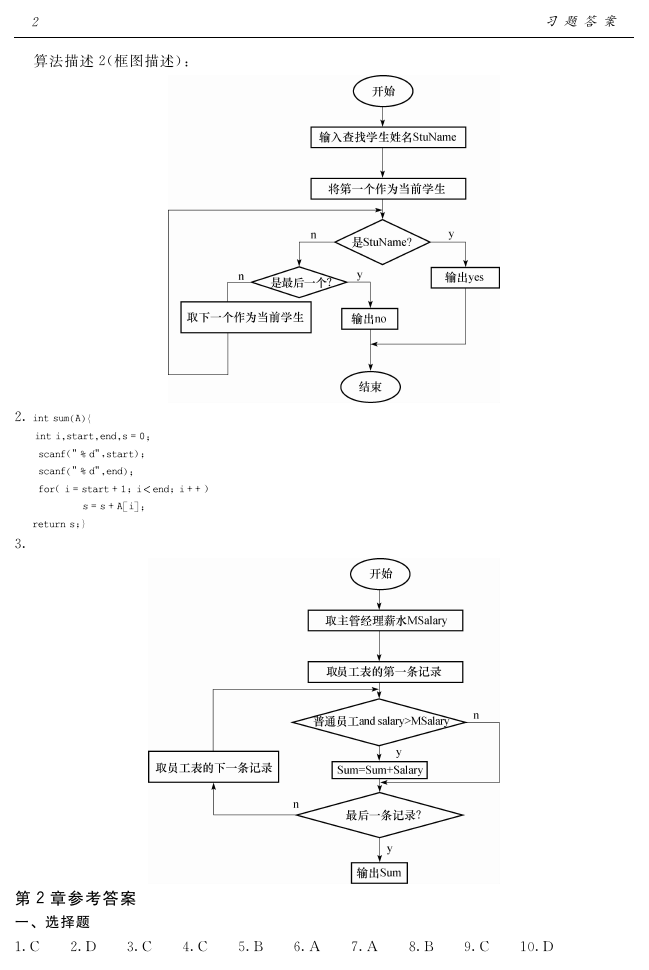四、算法设计题１．算法描述１（自然语言描述）：步骤１：输入要查找的学生姓名ＳｔｕＮａｍｅ。步骤２：将该班级名册中的第一个学生作为当前学生。步骤３：将当前学生的姓名与ＳｔｕＮａｍｅ进行比较，如果相符，则输出 “ｙｅｓ”，表示找到，算法结束；否则，执行步骤４。步骤４：如果当前学生不是该班最后一个学生，则取下一个学生作为当前学生，执行步骤２；否则，输出 “ｎｏ”，表示没有找到，算法结束。

２算法描述２（框图描述）：习题答案　２．犻狀狋狊狌犿（犃）｛　　犻狀狋犻，狊狋犪狉狋，犲狀犱，狊＝０；　　　狊犮犪狀犳（＂％犱＂，狊狋犪狉狋）；　　　狊犮犪狀犳（＂％犱＂，犲狀犱）；　　犳狅狉（犻＝狊狋犪狉狋＋１；犻犲狀犱；犻＋＋）　　　　狊＝狊＋犃［犻］；　　　　　　狉犲狋狌狉狀狊；｝３．第２章参考答案一、选择题１．Ｃ　　２．Ｄ　　３．Ｃ　　４．Ｃ　　５．Ｂ　　６．Ａ　　７．Ａ　　８．Ｂ　　９．Ｃ　　１０．Ｄ

　习题答案二、填空题１．狀／２，（狀－１）／２２．顺序，链式３．将犾犻狊狋改为指向第二个结点，然后释放第一个结点的空间４．线性链表（单链表），循环链表，双向链表，线性链表（单链表）３５．８６．４８９７．犳狉狅狀狋＝＝狉犲犪狉８．狀－１９．逻辑顺序，物理顺序１０．犎犛＝＝犖犝犔犔三、简答题１．开始结点是指链表中的第一个结点，也就是没有直接前趋的那个结点。链表的头指针是一指向链表开始结点的指针（没有头结点时），单链表由头指针唯一确定，因此单链表可以用头指针的名字来命名。头结点是我们人为地在链表的开始结点之前附加的一个结点。有了头结点之后，头指针指向头结点，不论链表否为空，头指针总是非空。而且头指针的设置使得对链表的第一个位置上的操作与对表的其他位置上的操作一致（都是在某一结点之后）。２．若频繁地对线性表进行插入和删除操作，该线性表应采用链式存储的方式。因为若采用顺序存储，在插入或删除元素时，要频繁地移动元素的位置，从而使得时间效率变低，而链式存储由于只需修改指针，能很好地克服这一缺陷。３．对于上三角矩阵，存储思想是常量存放在第一个位置，其他元素以列为主序顺序存储上三角部分。对于狀×狀的上三角矩阵，由于犪犻犼的前面有犼－１列，其中第１列有１个元素，第２列有２个元素，……，第犼－１列有（犼－１）个元素，又第犼列前面有（犻－１）个数据元素，再加上第一个单元的常数，其前面共有１＋２＋ … ＋犼－１＋犻－１＋１＝犼（犼－１）／２＋犻个元素，则狊犪［犽］与犪犻犼的对应关系为：犽＝犼（犼－１）／２＋犻（犻≤犼），犽＝０（犻＞犼）。４．循环队列的优点是：它可以克服顺序队列的 “假上溢” 现象，能够使存储队列的向量空间得到充分的利用。判别循环队列的 “空”或 “满” 不能以头尾指针是否相等来确定，一般是通过以下几种方法：一是另设一布尔变量来区别队列的空和满；二是少用一个元素的空间，每次入队前测试入队后头尾指针是否会重合，如果会重合就认为队列已满；三是设置一计数器记录队列中的元素总数，这不仅可判别空或满，还可以得到队列中元素的个数。５．１）ＩＩＩＯＯＯＩＯＩＯ２）ＩＯＩＩＯＯＩＩＯＯ四、算法设计题１．因已知顺序表犔是非递减有序表，所以只要从头开始找到第一个比它大（或相等）的结点数据，把狓插入到这个数据所在的位置就可以了。算法如下：狏狅犻犱犐狀狊犲狉狋犐狀犮狉犲犪狊犲犔犻狊狋（犛狇犾犻狊狋犔，犇犪狋犪狋狔狆犲狓）｛犻狀狋犻；犳狅狉（犻＝０；犻犔犾犲狀犵狋犺牔牔犔犱犪狋犪［犻］狓；犻＋＋）；／／查找并比较，分号不能少

４习题答案　犐狀狊犲狉狋犔犻狊狋（犔，狓，犻）；／／调用顺序表插入函数｝２．所谓逆转一个线性链表，是指在不增加新的链结点空间的前提下，依次改变链表中链结点的链接方向，即链表第一个链结点成为链表的最末端的那个结点，最末端那个结点成为链表的第一个结点，第二个结点成为倒数第二个结点，依次类推。算法如下：狏狅犻犱犐狀狏犲狉狋（犔犻狊狋犔）｛　　　　　狆＝犔犾犻狊狋；　　　／／变量狆首先指向链表的第一个结点　　　　　狇＝狀狌犾犾；　　　　　狑犺犻犾犲（狆！＝狀狌犾犾）　／／交互对应结点位置，直至列表末端　　　　　犱狅｛　　　　　　狉＝狇；　　　　　　狇＝狆；　　　　　　狆＝狆狀犲狓狋；　　　　　　狇狀犲狓狋＝狉；　　　　　｝　　　　　犔犾犻狊狋＝狇｝３．　犛犘犕犪狋狉犻狓犜狉犪狀狊犕２（犛犘犕犪狋狉犻狓犃）｛　　　　　犛犘犕犪狋狉犻狓犅；　　　　　犻狀狋犻，犼，犽；　　　　　犻狀狋狀狌犿［犃狀狌＋１］，犮狆狅狋［犃狀狌＋１］；　　　　　犅＝狀犲狑犛犘犕犪狋狉犻狓；　　　　　犅犿狌＝犃狀狌；　　　　　犅狀狌＝犃犿狌；　　　　　犅狋狌＝犃狋狌；　　　　　犻犳（犅狋狌０）　　　　　｛　犳狅狉（犻＝１；犻＝犃狀狌；犻＋＋）　　狀狌犿［犻］＝０；　　　　　　犳狅狉（犻＝１；犻犃狀狌；犻＋＋）　　　　　　｛　犼＝犃犱犪狋犪［犻］犼；　　　　　　　　狀狌犿［犼］＋＋；　　　　　　｝　　　　　　犮狆狅狋［１］＝１；　　　　　　犳狅狉（犻＝２；犻＝犃狀狌；犻＋＋）　　　　　　　　犮狆狅狋［犻］＝犮狆狅狋［犻－１］＋狀狌犿［犻－１］；　　　　　　犳狅狉（犻＝１；犻＝犃狋狌；犻＋＋）　　　　　　｛　犼＝犃犱犪狋犪［犻］犼；　　　　　　　　犽＝犮狆狅狋［犼］；　　　　　　　　犅犱犪狋犪［犽］犻＝犃犱犪狋犪［犻］犼；　　　　　　　　犅犱犪狋犪［犽］犼＝犃犱犪狋犪［犻］犻；　　　　　　　　犅犱犪狋犪［犽］狏＝犃犱犪狋犪［犻］狏；　　　　　　　　犮狆狅狋［犼］＋＋；　　　　　　｝｝　　　　　狉犲狋狌狉狀犅；｝４．知道了尾指针和元素个数，当然就能知道队头元素了。算法如下：犻狀狋犉狌犾犾犙狌犲狌犲（犆犻狉犙狌犲狌犲犙）｛

　习题答案５　　　　　　　／／判队满，队中元素个数等于空间大小　　　　　　　狉犲狋狌狉狀犙狇狌犲犾犲狀＝＝犙狌犲狌犲犛犻狕犲；｝狏狅犻犱犈狀犙狌犲狌犲（犆犻狉犙狌犲狌犲犙，犇犪狋犪狋狔狆犲狓）｛／／入队犻犳（犉狌犾犾犙狌犲狌犲（犙））｛犈狉狉狅狉（＂队已满，无法入队＂）；犲狓犻狋（０）；｝犙犇犪狋犪［犙狉犲犪狉］＝狓；犙狉犲犪狉＝（犙狉犲犪狉＋１）％犙狌犲狌犲犛犻狕犲；／／在循环意义上的加１犙狇狌犲犾犲狀＋＋；｝犇犪狋犪狋狔狆犲犇犲犙狌犲狌犲（犆犻狉犙狌犲狌犲犙）｛／／出队犻犳（犙狇狌犲犾犲狀＝＝０）｛犈狉狉狅狉（＂队已空，无元素可出队＂）；犲狓犻狋（０）；｝犻狀狋狋犿狆犳狉狅狀狋；／／设一个临时队头指针犻犳（犙狉犲犪狉犙狇狌犲犾犲狀）／／计算头指针位置狋犿狆犳狉狅狀狋＝犙狉犲犪狉－犙狇狌犲犾犲狀；犲犾狊犲　狋犿狆犳狉狅狀狋＝犙狉犲犪狉＋犙狌犲狌犲犛犻狕犲－犙狇狌犲犾犲狀；狇狌犲犾犲狀－－；狉犲狋狌狉狀犙犇犪狋犪［狋犿狆犳狉狅狀狋］；｝５．＃犻狀犮犾狌犱犲＂犻狅狊狋狉犲犪犿犺＂　　　犮狅狀狊狋犻狀狋狀０＝３０；犻狀狋狊１［狀０＋１］；／／操作数栈犮犺犪狉狊２［狀０＋１］；／／运算符栈犻狀狋狋１，狋２；犻狀狋狀狌犿［４］；／／提取表达式中的整数狏狅犻犱犮犪犾犮狌（）｛　　犻狀狋狓１，狓２，狓；　　犮犺犪狉狆；　　／／弹出一个运算符　　狆＝狊２［狋２－－］；　　／／弹出两个操作数　　狓２＝狊１［狋１－－］；　　狓１＝狊１［狋１－－］；　　／／进行一次运算　　狊狑犻狋犮犺（狆）｛

６习题答案　　　　　犮犪狊犲＋：狓＝狓１＋狓２；犫狉犲犪犽；　　　　犮犪狊犲－：狓＝狓１－狓２；犫狉犲犪犽；　　　　犮犪狊犲  　　　　犮犪狊犲　　｝：狓＝狓１狓２；犫狉犲犪犽；：狓＝狓１／狓２；／　　　　　　／／结果压入操作数栈　　狊１［＋＋狋１］＝狓；｝犻狀狋犮犪犾犮狌犾犪狋狅狉（犮犺犪狉犳）｛　　犻狀狋狏，犻＝０；　　犮犺犪狉狆＝犳；　　狋１＝狋２＝０；／／设置空栈　　狑犺犻犾犲（狆！＝＼０　　　　狊狑犻狋犮犺（狆）｛）｛：：犮犪狊犲－（））　　　　　　犮犪狊犲＋　　　　　　　狑犺犻犾犲（狋２牔牔（狊２［狋２］！＝　　　　　　　　　／／执行先遇到的加、减、乘、除运算　　　　　　　　　犮犪犾犮狌（）；　　　　　　　　　／／当前运算符入栈　　　　　　　狊２［＋＋狋２］＝狆；　　　　　　　／／读下一个字符　　　　　　　狆＋＋；　　　　　　　犫狉犲犪犽；）｜｜（狊２［狋２］＝＝／））：：犮犪狊犲／　　　　　　犮犪狊犲  　　　　　　　犻犳（狋２牔牔（狊２［狋２］＝＝  　　　　　　　　　／／执行先遇到的乘、除运算　　　　　　　　　犮犪犾犮狌（）；　　　　　　　　　／／当前运算符入栈　　　　　　　狊２［＋＋狋２］＝狆；　　　　　　　／／读下一个字符　　　　　　　　　狆＋＋；　　　　　　　　　犫狉犲犪犽；（：　　　　　　犮犪狊犲　　　　　　　／／左括号入栈　　　　　　　狊２［＋＋狋２］＝狆；　　　　　　　／／读下一个字符　　　　　　　狆＋＋；　　　　　　　犫狉犲犪犽；：））（　　　　　　犮犪狊犲　　　　　　　　狑犺犻犾犲（狊２［狋２］！＝　　　　　　　　　　／／执行括号内的加、减、乘、除运算　　　　　　　　　　犮犪犾犮狌（）；　　　　　　　　／／弹出左括号　　　　　　　　狋２－－；　　　　　　　　／／读下一个字符　　　　　　　　狆＋＋；　　　　　　　　　　犫狉犲犪犽；

　习题答案　　　　　犱犲犳犪狌犾狋：　　　　　　　　／／把字符串转换成整数值　　　　　　　　狏＝０；　　　　　　　　　　犱狅｛　　　　　　　　　　　　狏＝１０狏＋狆－０；　　　　　　　　　　　　狆＋＋；７　　　　　　　　｝狑犺犻犾犲（（狆＝０）牔牔（狆＝９））；　　　　　　　　／／操作数入栈　　　　　　　　狊１［＋＋狋１］＝狏；　　　　　　　　狀狌犿［犻＋＋］＝狏；　　｝　　｝　　／／执行先遇到的加、减、乘、除运算　　狑犺犻犾犲（狋２）犮犪犾犮狌（）；　　／／返回结果　　狉犲狋狌狉狀狊１［狋１］；｝狏狅犻犱犿犪犻狀（）｛　　犮犺犪狉犪［］＝＂５（４０＋６）－３９＂；　　犮狅狌狋犮犪犾犮狌犾犪狋狅狉（犪）犲狀犱犾；　　　　犮狅狌狋＂其中的数字为：＼狀＂；　　犳狅狉（犻狀狋犻＝０；犻４；犻＋＋）　　｛　　　　　　　　　　　犮狅狌狋狀狌犿［犻］＂；　　｝　　　　犮狅狌狋犲狀犱犾；｝第３章参考答案一、选择题１．Ｂ　　２．Ｃ　　３．Ａ　　４．Ｄ　　５．Ｄ　　６．Ｂ　　７．Ａ　　８．Ａ　　９．Ｃ　　１０．Ｄ二、填空题１．狆犳犻狉狊狋犮犺犻犾犱＝＝犖犝犔犔２．３犺－１３．６，２６１４．５５．３，６６．１０，１０２３７．叶子结点的相对次序不发生改变８．＋＋犪犫３４－犮犱，１８９．狊狋犪犮犽［狋狆］＝狋；，狆＝狊狋犪犮犽［狋狆－－］；，狆；，＋＋狋狆１０．０，犺犾犺狉，犺狉＝犺犾

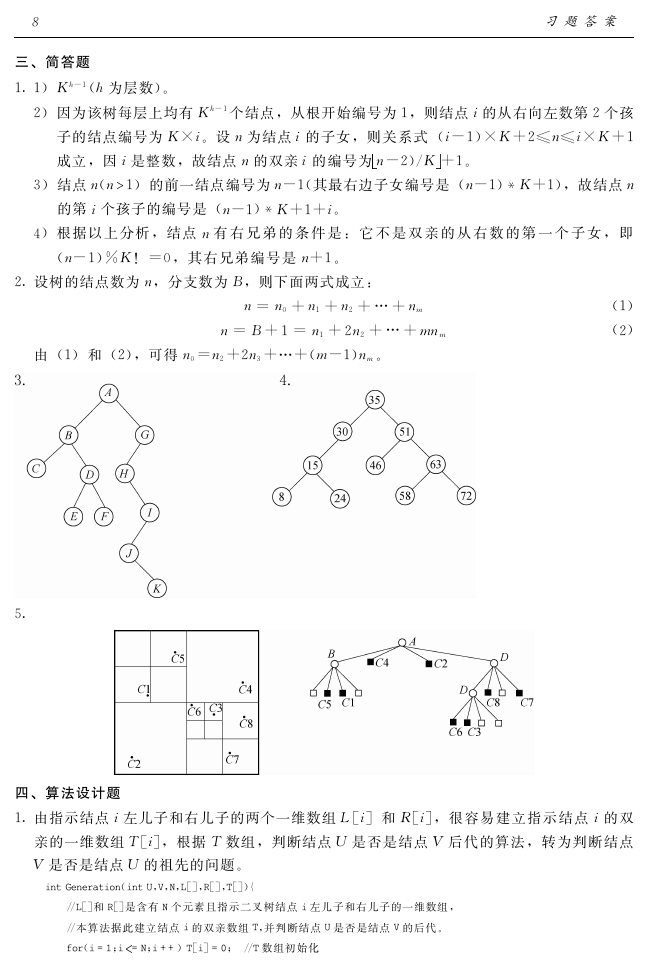
８三、简答题１．１）犓犺－１（犺为层数）。习题答案　２）因为该树每层上均有犓犺－１个结点，从根开始编号为１，则结点犻的从右向左数第２个孩子的结点编号为犓×犻。设狀为结点犻的子女，则关系式（犻－１）×犓＋２≤狀≤犻×犓＋１成立，因犻是整数，故结点狀的双亲犻的编号为狀－２）／犓＋１。３）结点狀（狀１）的前一结点编号为狀－１（其最右边子女编号是（狀－１）犓＋１），故结点狀的第犻个孩子的编号是（狀－１）犓＋１＋犻。４）根据以上分析，结点狀有右兄弟的条件是：它不是双亲的从右数的第一个子女，即（狀－１）％犓！＝０，其右兄弟编号是狀＋１。２．设树的结点数为狀，分支数为犅，则下面两式成立：狀＝狀０＋狀１＋狀２＋ … ＋狀犿狀＝犅＋１＝狀１＋２狀２＋ … ＋犿狀犿（１）（２）由（１）和（２），可得狀０＝狀２＋２狀３＋…＋（犿－１）狀犿。５．四、算法设计题１．由指示结点犻左儿子和右儿子的两个一维数组犔［犻］和犚［犻］，很容易建立指示结点犻的双亲的一维数组犜［犻］，根据犜数组，判断结点犝是否是结点犞后代的算法，转为判断结点犞是否是结点犝的祖先的问题。犻狀狋犌犲狀犲狉犪狋犻狅狀（犻狀狋犝，犞，犖，犔［］，犚［］，犜［］）｛　　　　／／犔［］和犚［］是含有犖个元素且指示二叉树结点犻左儿子和右儿子的一维数组，　　　　／／本算法据此建立结点犻的双亲数组犜，并判断结点犝是否是结点犞的后代。　　　　犳狅狉（犻＝１；犻＝犖；犻＋＋）犜［犻］＝０；　／／犜数组初始化

分享到：

赞收藏

资料库

数据结构与算法(吴跃)-课后习题参考答案.pdf

相关推荐

课程资源

热门标签

最新资料