logo资料库

八数码问题实验报告.doc

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.16M 资料格式：doc 举报 版权申诉
第1页 / 共12页
第2页 / 共12页
第3页 / 共12页
第4页 / 共12页
第5页 / 共12页
第6页 / 共12页
第7页 / 共12页
第8页 / 共12页
资料共12页，剩余部分请下载后查看
    人工智能实验报告
    一、实验目的
    二、实验内容
    三、实验分析
    四、源代码及运行结果
    人工智能实验报告 八 数 码 问 题 姓名 马鹏 学号 2402100230
    一、实验目的 1. 熟悉人工智能系统中的问题求解过程； 2. 熟悉状态空间的盲目搜索和启发式搜索算法的应用； 3. 熟悉对八数码问题的建模、求解及编程语言的应用 二、实验内容 八数码问题：在 3×3 的方格棋盘上，摆放着 1 到 8 这八个数码，有 1 个方 格是空的，其初始状态如图 1 所示，要求对空格执行空格左移、空格右移、空格 上移和空格下移这四个操作使得棋盘从初始状态到目标状态。 2 1 7 8 6 3 4 5 1 8 7 2 6 3 4 5 (a) 初始状态 (b) 目标状态 图 1 八数码问题示意图 三、实验分析 1.结点状态 采用了 struct Node 数据类型 typedef struct _Node{ int digit[ROW][COL]; int dist; int dep; // 一个表和目的表的距离 // 深度 //dist + dep.估价函数值 int index; // 父节点的位置 } Node; 2.发生器函数 定义的发生器函数由以下的四种操作组成： (1)将当前状态的空格上移 Node node_up; Assign(node_up, index);//向上扩展的节点 int dist_up = MAXDISTANCE; (2)将当前状态的空格下移 Node node_down; Assign(node_down, index);//向下扩展的节点 int dist_down = MAXDISTANCE;
    (3)将当前状态的空格左移 Node node_left; Assign(node_left, index);//向左扩展的节点 int dist_left = MAXDISTANCE; (4)将当前状态的空格右移 Node node_right; Assign(node_right, index);//向右扩展的节点 int dist_right = MAXDISTANCE; 通过定义结点状态和发生器函数，就解决了 8 数码问题的隐式图的生成问 题。接下来就是搜索了。 3.图的搜索策略 经过分析，8 数码问题中可采用的搜速策略共有：1.广度优先搜索、2.深度 优先搜索、2.有界深度优先搜索、4.最好优先搜索、5.局部择优搜索，一共五种。 其中，广度优先搜索法是可采纳的，有界深度优先搜索法是不完备的，最好优先 和局部择优搜索法是启发式搜索法。 实验时,采用了广度(宽度)优先搜索来实现。 （三、）广度(宽度)优先搜索原理 1. 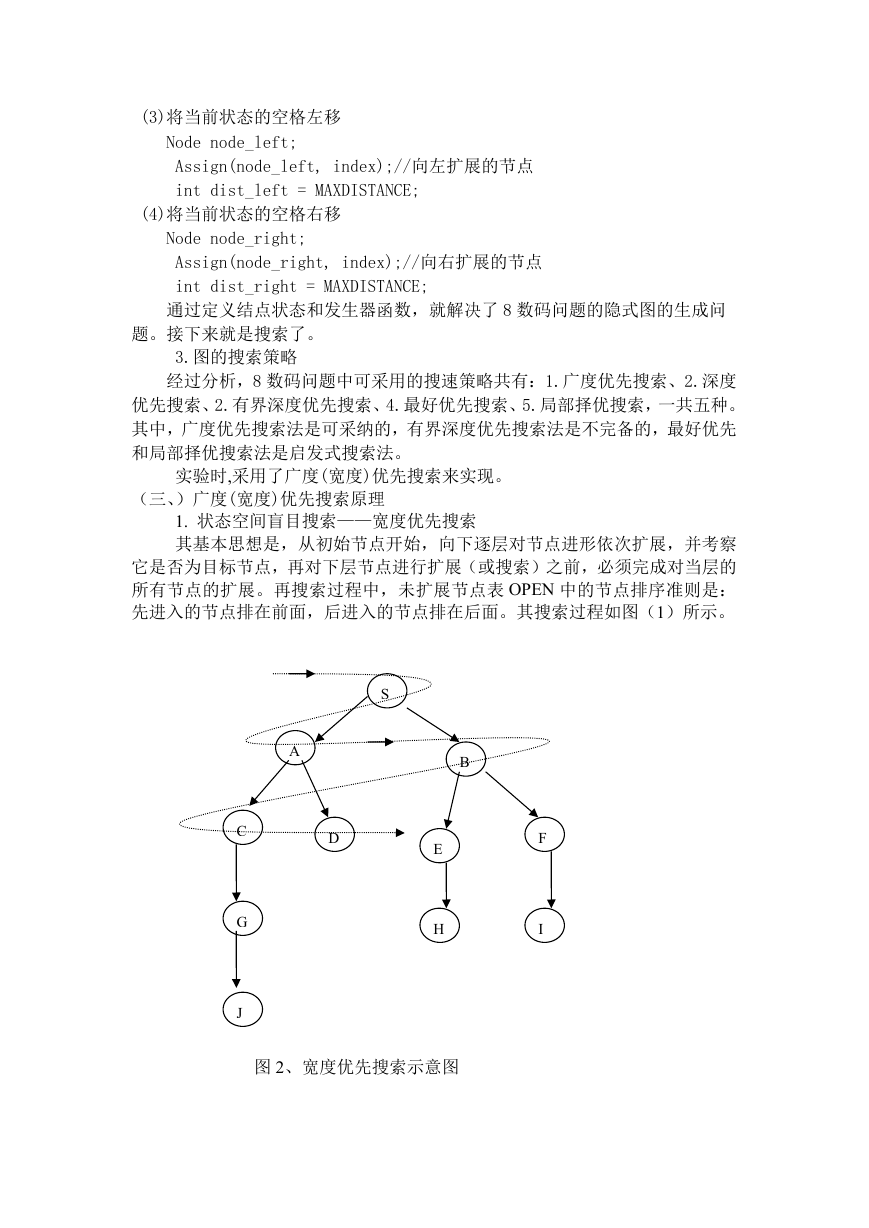状态空间盲目搜索——宽度优先搜索 其基本思想是，从初始节点开始，向下逐层对节点进形依次扩展，并考察 它是否为目标节点，再对下层节点进行扩展（或搜索）之前，必须完成对当层的 所有节点的扩展。再搜索过程中，未扩展节点表 OPEN 中的节点排序准则是： 先进入的节点排在前面，后进入的节点排在后面。其搜索过程如图（1）所示。 S A D B E H F I C G J 图 2、宽度优先搜索示意图
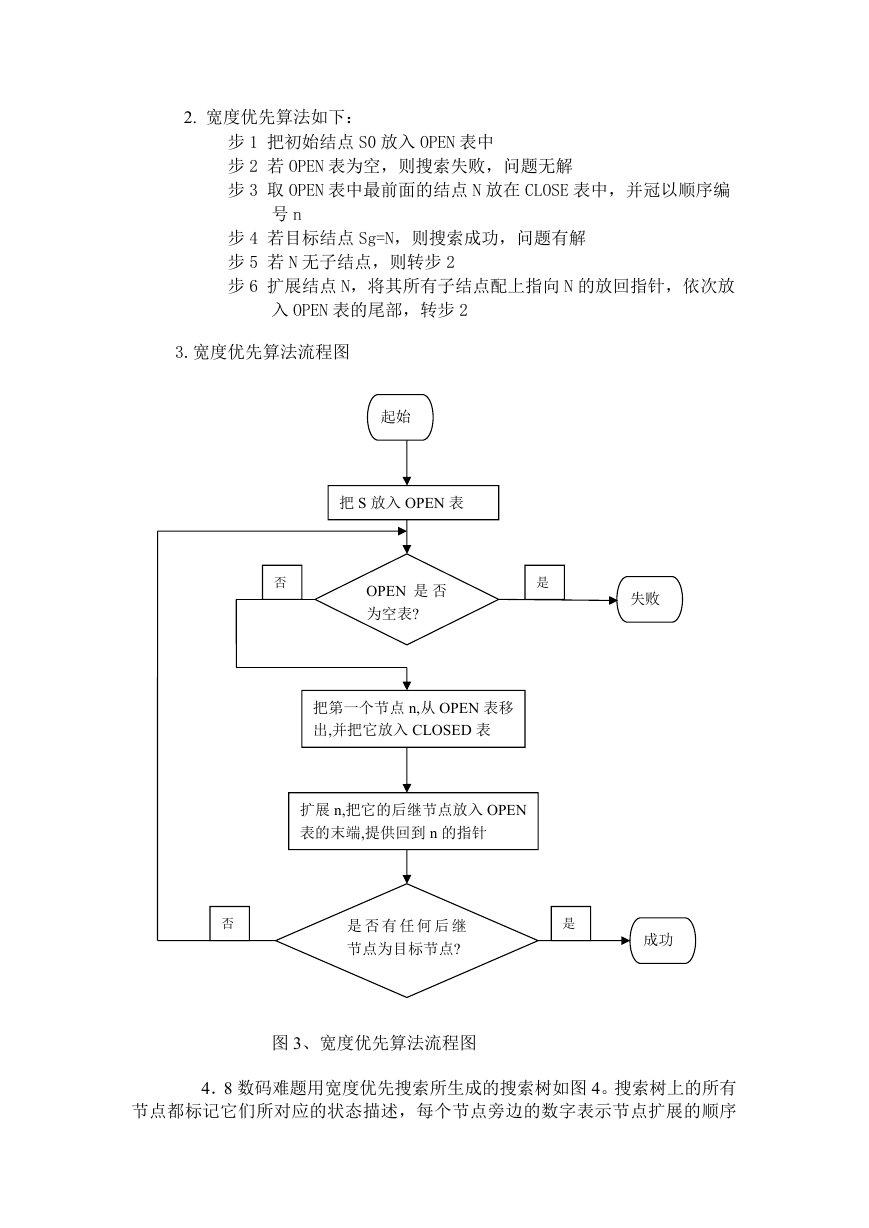
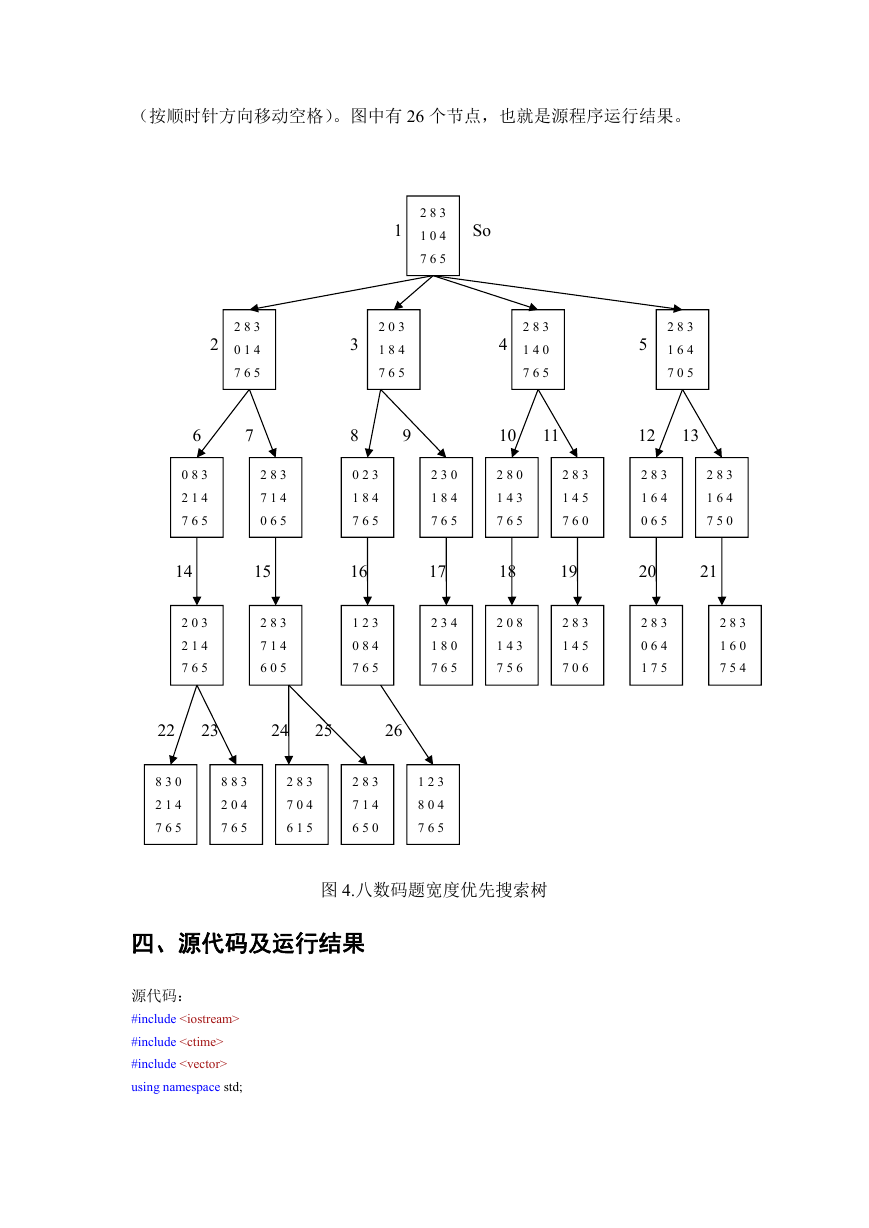
    2. 宽度优先算法如下： 步 1 把初始结点 S0 放入 OPEN 表中 步 2 若 OPEN 表为空，则搜索失败，问题无解 步 3 取 OPEN 表中最前面的结点 N 放在 CLOSE 表中，并冠以顺序编 号 n 步 4 若目标结点 Sg=N，则搜索成功，问题有解 步 5 若 N 无子结点，则转步 2 步 6 扩展结点 N，将其所有子结点配上指向 N 的放回指针，依次放 入 OPEN 表的尾部，转步 2 3.宽度优先算法流程图 起始 把 S 放入 OPEN 表 否 OPEN 是 否 为空表? 是 失败 把第一个节点 n,从 OPEN 表移 出,并把它放入 CLOSED 表 扩展 n,把它的后继节点放入 OPEN 表的末端,提供回到 n 的指针 否 是 否 有 任 何 后 继 节点为目标节点? 是 成功 图 3、宽度优先算法流程图 4．8 数码难题用宽度优先搜索所生成的搜索树如图 4。搜索树上的所有 节点都标记它们所对应的状态描述，每个节点旁边的数字表示节点扩展的顺序
    （按顺时针方向移动空格）。图中有 26 个节点，也就是源程序运行结果。 1 2 8 3 1 0 4 7 6 5 So 2 2 8 3 0 1 4 7 6 5 6 0 8 3 2 1 4 7 6 5 7 2 8 3 7 1 4 0 6 5 14 15 2 0 3 2 1 4 7 6 5 2 8 3 7 1 4 6 0 5 2 0 3 1 8 4 7 6 5 4 2 8 3 1 4 0 7 6 5 5 2 8 3 1 6 4 7 0 5 9 10 11 12 13 3 8 0 2 3 1 8 4 7 6 5 16 1 2 3 0 8 4 7 6 5 2 3 0 1 8 4 7 6 5 17 2 3 4 1 8 0 7 6 5 2 8 0 1 4 3 7 6 5 18 2 0 8 1 4 3 7 5 6 2 8 3 1 4 5 7 6 0 19 2 8 3 1 4 5 7 0 6 2 8 3 1 6 4 0 6 5 2 8 3 1 6 4 7 5 0 20 21 2 8 3 0 6 4 1 7 5 2 8 3 1 6 0 7 5 4 22 23 24 25 26 8 3 0 2 1 4 7 6 5 8 8 3 2 0 4 7 6 5 2 8 3 7 0 4 6 1 5 2 8 3 7 1 4 6 5 0 1 2 3 8 0 4 7 6 5 图 4.八数码题宽度优先搜索树 四、源代码及运行结果 源代码： #include #include #include using namespace std;
    const int ROW = 3;//行数 const int COL = 3;//列数 const int MAXDISTANCE = 10000;//最多可以有的表的数目 const int MAXNUM = 10000; typedef struct _Node{ // 一个表和目的表的距离 // 深度 int digit[ROW][COL]; int dist; int dep; // dist + dep.估价函数值 int index; //父节点的位置 } Node; Node src, dest;// 父节表目的表 vector node_v; //存储节点 bool isEmptyOfOPEN() //open表是否为空 { for (int i = 0; i < node_v.size(); i++) { if (node_v[i].dist != MAXNUM) return false; } return true; } bool isEqual(int index, int digit[][COL]) //判断这个最优的节点是否和目的节点一样 { for (int i = 0; i < ROW; i++) for (int j = 0; j < COL; j++) { if (node_v[index].digit[i][j] != digit[i][j]) return false; } return true; } ostream& operator<<(ostream& os, Node& node) { for (int i = 0; i < ROW; i++) { for (int j = 0; j < COL; j++) os << node.digit[i][j] << ' '; os << endl; } return os;
    } void PrintSteps(int index, vector& rstep_v)//输出每一个遍历的节点深度遍历 { rstep_v.push_back(node_v[index]); index = node_v[index].index; while (index != 0) { rstep_v.push_back(node_v[index]); index = node_v[index].index; } for (int i = rstep_v.size() - 1; i >= 0; i--)//输出每一步的探索过程 cout << "Step " << rstep_v.size() - i << endl << rstep_v[i] << endl; } void Swap(int& a, int& b) { int t; t = a; a = b; b = t; } void Assign(Node& node, int index) { for (int i = 0; i < ROW; i++) for (int j = 0; j < COL; j++) node.digit[i][j] = node_v[index].digit[i][j]; } int GetMinNode() //找到最小的节点的位置即最优节点 { // the location of minimize node int dist = MAXNUM; int loc; for (int i = 0; i < node_v.size(); i++) { if (node_v[i].dist == MAXNUM) continue; else if ((node_v[i].dist + node_v[i].dep) < dist) { loc = i; dist = node_v[i].dist + node_v[i].dep; }
    } return loc; } bool isExpandable(Node& node) { for (int i = 0; i < node_v.size(); i++) { if (isEqual(i, node.digit)) return false; } return true; } int Distance(Node& node, int digit[][COL]) { int distance = 0; bool flag = false; for(int i = 0; i < ROW; i++) for (int j = 0; j < COL; j++) for (int k = 0; k < ROW; k++) { for (int l = 0; l < COL; l++) { if (node.digit[i][j] == digit[k][l]) { distance += abs(i - k) + abs(j - l); flag = true; break; } else flag = false; } if (flag) break; } return distance; } int MinDistance(int a, int b) { return (a < b ? a : b); } void ProcessNode(int index) { int x, y;
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料