logo资料库

浙大应用光学课件.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书 资料大小：2.04M 资料格式：pdf 举报 版权申诉
第1页 / 共51页
第2页 / 共51页
第3页 / 共51页
第4页 / 共51页
第5页 / 共51页
第6页 / 共51页
第7页 / 共51页
第8页 / 共51页
资料共51页，剩余部分请下载后查看
    app_opt1.pdf
    APP_OPT2
    APP_OPT3
    APP_OPT4
    app_opt5
    APP_OPT6
    app_opt7-1黑白
    app_opt7-2黑白
    app_opt7-3黑白
    app_opt7-4黑白
    app_opt8-1黑白
    app_opt8-2黑白
    app_opt8-3黑白
    app_opt10(05)黑白
    review黑白
    第一章 几何光学的基本定律 §1－1 发光点、波面、光线和光束 §1－2 几何光学的基本定律 §1－3 费马原理 §1－1 发光点、波面、光线和光束 • 发光点——本身发光或被照明后发光的几何点。既无大小又无体 积，但能辐射能量。 • 波面——发光点在某一时刻发出的光形成波面。若周围是各向同 性均匀介质，将形成以发光点为中心的球面波（平面波） • 光线——波面的法线即几何光学中所指的光线 • 光束——波面的法线族 §1－4 物、像的基本概念和完善成像条件 光学系统 • 光束与波面的对应关系： 平行光束——平面波 同心光束——球面波 发散光束 会聚光束 理想光学系统 发光点——————》点 同心光束——》同心光束 实际光学系统 发光点——————》斑 同心光束——》非同心光束 §1－2 几何光学的基本定律 几何光学 光的传播————》光线传播 • 一、光的直线传播定律：光在各向同性的均匀 介质中沿直线传播。 衍射：sinα=Kλ/D 当λ——>0时，波动光学——》几何光学 • 二、光的独立传播定律：以不同途径传播的光同时在 空间某点相遇时，彼此互不影响，独立传播。相遇处 的光强度是简单地相加，总是增强的。 屏上被两发光点同时照亮 区域的照度等于二发光点 产生的照度之和。 忽略干涉现象 1 EEE += 干涉： 2 2EI = I E 2 2 1 = = I 1 E 2 2 三、反射定律与折射定律 • AO——入射光线 I ——入射角 • OC——反射光线 I”——反射角 • OB——折射光线 I’——折射角 • NN’——法线 A P 光的反射定律： ①入射光线、法线和反射光线在同一平面内； ②入射光线与反射光线在法线的两侧，且有 I”= -I N -I” I O I’ N’ C n n’ Q B 1
    光的折射定律： ①入射光线、法线和折射光线在同一平面内； ②折射角和入射角的正弦之比在一定温度和压力下对一定波 长的光线而言为一常量，与入射角和大小无关。即 或 ' I sin = I sin n nI sin' ' = n n ' I sin 其中：n=C/v C——光在真空中的速度 v——光在介质中的速度 因为 v1 空气中 n=1.000272 (760mmHg, 20°C， λ=0.5893μ） 与空气比较的折射率——相对折射率 四、光线传播的可逆性 • 令CO为入射光线，则OA为反射光 线（反射定律） • 令BO为入射光线，则OA为折射光 线（折射定律） A P 在折射定律中，若令n’= - n , 即得 I’= - I 反射定律是折射定律当n’= - n时的特殊情况 空气中反射时，可认为 n=1, n’= - 1 利用以上定律，可解决光经任何界面 后继续传播的问题，是整个应用光学 的基础 C Q n n’ I O -I” I’ B 几何光学 四大定律 • – 入射光 – 全反射 反射——一定存在 A N C 折射——特定条件下可能 A Im 没有，即全反射。 • 当光疏——>光密，即n光疏，即n>n’时，sinI’ 可能大于1，此时全反射。 • 当sinI’=1时，I’=90°，此时的 I =Im P 称临界角 I” I O I’ N’ C B Q sinIm=n’/n 当I≥Im 时，将发生全反射 全反射的应用 • ①等腰直角棱镜 – 当2U在某范围内 时,斜面上发生全反 射,则透明介质界面 上不需要镀反射膜 ②光导纤维 I>Im时全反射,用于 传像和传光 低n1透明玻璃体 高n2玻璃芯子 矢量形式的折射定律和反射定律 A0——沿入射光线的单位矢量 A0’——沿折射光线的单位矢量 N——沿法线的单位矢量 n’sinI’=n sinI ' ×N)＝n(A0 ×N) 即 n'(A0 将长度为n’的折射光线矢量和长度 为n的入射光线矢量分别记为A’和A， 则 A'×N＝A×N 即 (A'-A)×N＝0 所以, A’-A与N平行, 可写为 A'-A＝PN (P为待定常数) I I’ A n n’>n A’ A0 A0’ N A’ N A N n n’
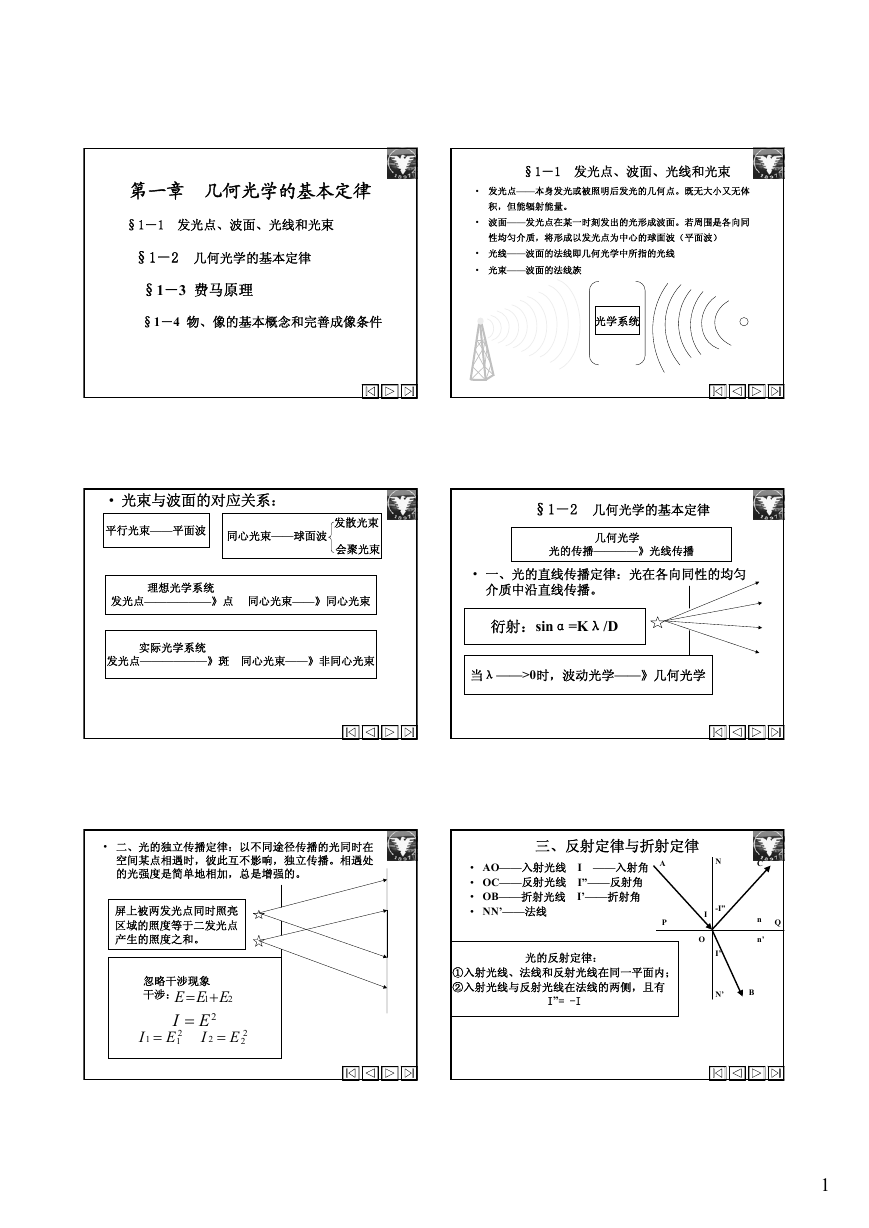
    §1－3 费马原理 • 费马原理从光程的观点来描述光传播的规律， 是几何光学最基本的定律。 • 一、光程——光线在介质中传播的距离与该介质 折射率的乘积。 • 1.均匀介质中， s＝nl • 由于n＝C/v, l＝vt, 所以 s＝Ct • ——光线在介质中传播的光程等于光线从一点到另 一点传播的时间与在真空中传播速度的乘积。 • ——光线在真空中相同时间内传播的距离。 • 2.非均匀介质中：ds=ndl n B • 如右图， 光程A——》B A a n1 b n2 1 dncnbnans = + + 3 4 cbnda ) ++= + 2 ( + n3 c n4 d B s ∫= B A zyxn ( , , ) dl dl A 费马原理 • 光从一点传播到另一点是沿着光程为极值 （极大、极小、常量）的路径传播的。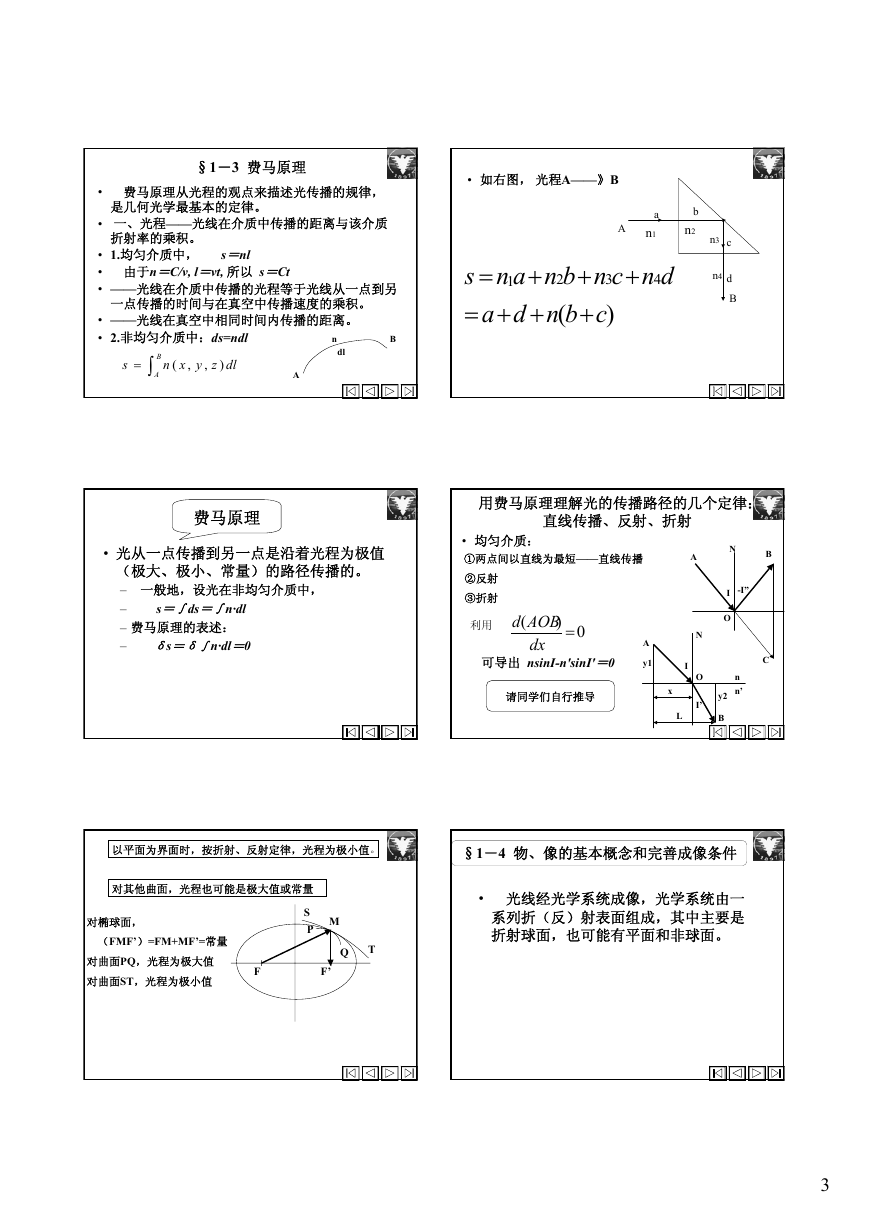 – 一般地，设光在非均匀介质中， – – 费马原理的表述： – δs＝δ∫n·dl＝0 s＝∫ds＝∫n·dl 用费马原理理解光的传播路径的几个定律： 直线传播、反射、折射 • 均匀介质： ①两点间以直线为最短——直线传播 A N B ②反射 ③折射 利用 d ( 0) = AOB dx 可导出 nsinI-n'sinI'＝0 请同学们自行推导 -I” I O n n’ y2 B C A y1 N O I’ I x L 以平面为界面时，按折射、反射定律，光程为极小值。 §1－4 物、像的基本概念和完善成像条件 对其他曲面，光程也可能是极大值或常量 对椭球面， （FMF’）=FM+MF’=常量 对曲面PQ，光程为极大值 对曲面ST，光程为极小值 S P M Q T F F’ • 光线经光学系统成像，光学系统由一 系列折（反）射表面组成，其中主要是 折射球面，也可能有平面和非球面。 3
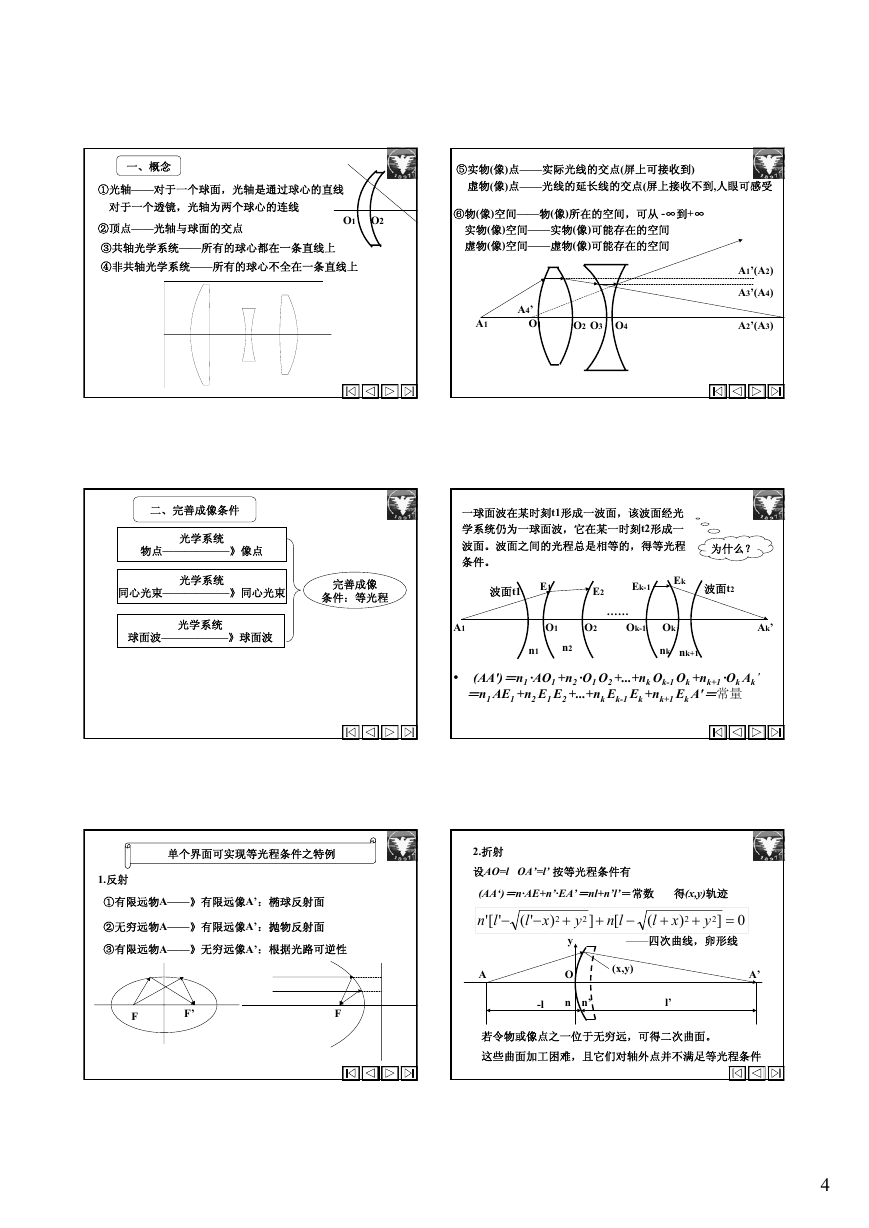
    一、概念 ①光轴——对于一个球面，光轴是通过球心的直线 ⑤实物(像)点——实际光线的交点(屏上可接收到) 虚物(像)点——光线的延长线的交点(屏上接收不到,人眼可感受 对于一个透镜，光轴为两个球心的连线 ②顶点——光轴与球面的交点 ③共轴光学系统——所有的球心都在一条直线上 ④非共轴光学系统——所有的球心不全在一条直线上 O1 O2 ⑥物(像)空间——物(像)所在的空间，可从 -∞到+∞ 实物(像)空间——实物(像)可能存在的空间 虚物(像)空间——虚物(像)可能存在的空间 A1 A4’ O1 O3O2 O4 A1’(A2) A3’(A4) A2’(A3) 二、完善成像条件 光学系统 物点——————》像点 一球面波在某时刻t1形成一波面，该波面经光 学系统仍为一球面波，它在某一时刻t2形成一 波面。波面之间的光程总是相等的，得等光程 条件。 为什么？ 光学系统 同心光束——————》同心光束 完善成像 条件：等光程 波面t1 E1 Ek-1 Ek 波面t2 E2 …… 光学系统 球面波——————》球面波 A1 O1 O2 Ok-1 n1 n2 Ok nk nk+1 Ak’ • (AA')＝n1 ·AO1 +n2 ·O1 O2 +...+nk Ok-1 Ok +nk+1 ·Ok Ak ＝n1 AE1 +n2 E1 E2 +...+nk Ek-1 Ek +nk+1 Ek A'＝常量 ' 单个界面可实现等光程条件之特例 1.反射 ①有限远物A——》有限远像A’：椭球反射面 ②无穷远物A——》有限远像A’：抛物反射面 ③有限远物A——》无穷远像A’：根据光路可逆性 F F’ F 2.折射 设AO=l OA’=l’ 按等光程条件有 (AA‘)＝n·AE+n’·EA’＝nl+n’l’＝常数 得(x,y)轨迹 ln '[' ] − xl '( − ln [ + + y ] ) 2 ) x l ( 0 = − ——四次曲线，卵形线 + y 2 2 2 + y A (x,y) O n n’ -l l’ A’ 若令物或像点之一位于无穷远，可得二次曲面。 这些曲面加工困难，且它们对轴外点并不满足等光程条件 4
    本章小结 发光点、光线和光束的概念 有关光传播路径的定律，特别是折射定律、反射定律 费马原理（极端光程定律） 物像概念，物空间、像空间，完善成像（等光程条件） 与本章内容有关的前沿问题 非球面及其应用 5
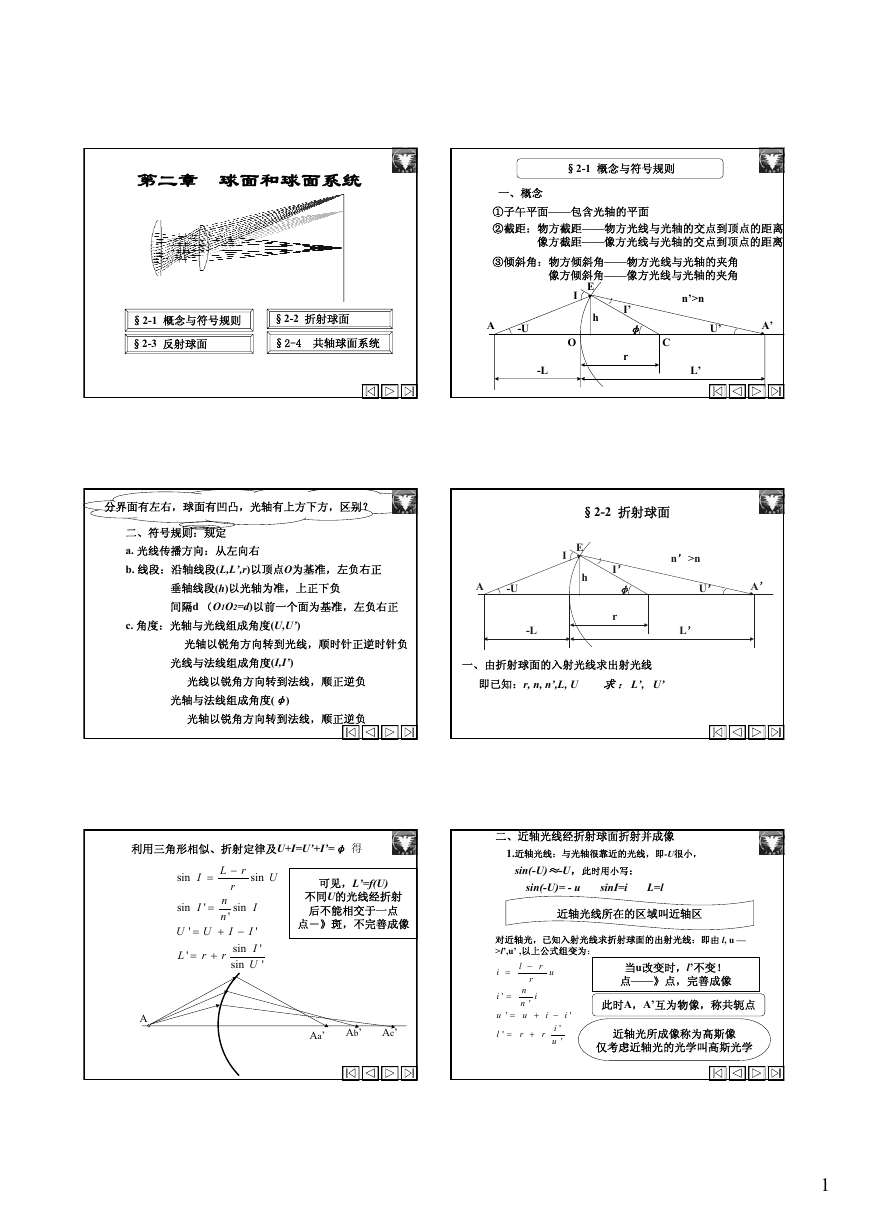
    第二章 球面和球面系统 §2-1 概念与符号规则 一、概念 ①子午平面——包含光轴的平面 ②截距：物方截距——物方光线与光轴的交点到顶点的距离 像方截距——像方光线与光轴的交点到顶点的距离 §2-1 概念与符号规则 §2-2 折射球面 §2-3 反射球面 §2-4 共轴球面系统 I O A -U -L E h I’ φ r n’>n C L’ U’ A’ ③倾斜角：物方倾斜角——物方光线与光轴的夹角 像方倾斜角——像方光线与光轴的夹角 分界面有左右，球面有凹凸，光轴有上方下方，区别？ 二、符号规则：规定 a. 光线传播方向：从左向右 b. 线段：沿轴线段(L,L’,r)以顶点O为基准，左负右正 垂轴线段(h)以光轴为准，上正下负 间隔d （O1O2=d)以前一个面为基准，左负右正 c. 角度：光轴与光线组成角度(U,U’) 光轴以锐角方向转到光线，顺时针正逆时针负 光线与法线组成角度(I,I’) 光线以锐角方向转到法线，顺正逆负 光轴与法线组成角度(φ) 光轴以锐角方向转到法线，顺正逆负 §2-2 折射球面 E I h I’ φ r n’>n U’ A’ L’ A -U -L 一、由折射球面的入射光线求出射光线 即已知：r, n, n’,L, U 求：L’, U’ 利用三角形相似、折射定律及U+I=U’+I’=φ 得 可见，L’=f(U) 不同U的光线经折射 后不能相交于一点 点－》斑，不完善成像 sin U I I ' I U ' ' r − r sin ' I − sin sin sin I = sin I ' = U ' = U L n n + L ' = r + r A Aa’ Ab’ Ac’ l ' = r + r 二、近轴光线经折射球面折射并成像 1.近轴光线：与光轴很靠近的光线，即-U很小， sin(-U)≈-U，此时用小写： sin(-U)= - u sinI=i L=l 近轴光线所在的区域叫近轴区 对近轴光，已知入射光线求折射球面的出射光线：即由 l, u — >l’,u’ ,以上公式组变为： r u 当u改变时，l’不变！ 点——》点，完善成像 i i = ' = u ' = − r ' l n n u i + i ' i − i u ' ' 此时A，A’互为物像，称共轭点 近轴光所成像称为高斯像 仅考虑近轴光的光学叫高斯光学 1
    2.近轴光线经折射球面计算的其他形式 （为计算方便，根据不同情况可使用不同公式） 利用 ' iu ulh lu ' == rh iu / ' φ +=+= = ni in ' ' = ' 可导出 n − )11( l r n n ' l l ' nu un ' =− ' − = n 11(' − r l ' nn ' − r nn ' − r h = 阿贝不变量 ) = Q 折射球面的物像位置关系 光线经折射球面时 的u,u’关系 3.（近轴区）折射球面的光焦度，焦点和焦距 可见，当（n’-n）/r一定时，l’仅与l有关。 正负含义？ = φ f f ' = l ' l −∞→ = = l l ' ∞→ −= n ' nn ' − n nn ' − 由上三式得 n f ' ' −= =φ ' f f −= ' n n nn − ' r r r n f 光焦度 （折射面偏折光线的能力） f’像方焦距（点），后焦距（点） l→-∞ F O -f f’ f 物方焦距（点），前焦距（点） l’→∞ F’ 普适于任何 光学系统 及 f l f ' ' ' + + f f l = = 1 r 三、物平面以细光束经折射球面成像 3. 细小平面以细光束成像的三种放大率与拉氏不变量 1.物平面以细小光束成像 A1 C A2 B1 A B2 A2’ B2’ A’ B1’ A1’ 细光束，A——》A’ 完善成像 同心球面A1AA2——》曲面A1’A’A2’ 完善成像 由公式，l变小，l’也变小，平面B1AB2——》曲面B1’A’B2’ 不再是平面：像面弯曲 2. 细小平面以细光束经折射球面成像： 平面物——》平面像，完善成像 B y A n n’ -l r l’ A’ -y’ B’ ①横向放大率（垂轴放大率）β = = y ' y =β nl ' ln ' nu un ' ②轴向（沿轴）放大率α nl ' ln ' u ' u ③角度放大率 dl dl γ α = = = 2 2 ' （利用三角形相似和阿贝不变量） ' = n ' n 2 β 描述光轴上一对共轭点沿轴 移动量之间的关系 == l l ' n n ' 1 β 描述折射前后一对光线与光轴夹 角之间的关系 =β 讨论： nl ' ln ' y' y =β 当n,n’一定， l不同，则β不同 当l一定(l’一定)时，β为常量。 垂轴物像 相似 β>0时，y,y’同号，成正像，否则成倒像 |β|>1时，|y’|>|y|, 成放大像，否则成缩小像 §2-3 反射球面——球面镜 一、物像公式 n ' l ' =− n l nn ' − r n’=-n 1 l ' =+ 1 l 2 r −=φ n2 r r<0, φ>0会聚 r>0, φ<0发散 二、焦距 f ' = f = r 2 f ’,f 与 r 同号 2 βα = n ' n α>0, 像移动方向与物移动方向相同 一般α≠β，立体物与像不再相似 βαγ= β、α、γ之间的关系 由 y ' y = β = nu un ' 得' nyu = uyn ' ' ' = j j为拉氏不变量， 它是表征光学系统 性能的重要参数 C F’ F f’<0为实焦点 三、放大率与拉氏不变量 β −= α −= γ −= 2 ' l l β 1 β FF’ C f’>0为虚焦点 （物像反向移动） j ∴ = yu nyu uyn ' ' = uy ' −= ' ' 2
    §2－4 共轴球面系统 B1 y1 A1 -u1 n1 O1 -l1 r1 n1’=n2 n2’=n3 u1’ C1 A1’(A2) u2 -y1’ -y2 B1’(B2) O2 C2 l1’ d1 -l2 r2 l2’ B2’ A2’ y2’ -u2’ 一、由入射光线求出射光线 对一个面的操作 + 过渡 过渡公式： = = = 1 i n i y u i l = = + + i (, = 1 i (, = 1 i (, = 1 + d i ' (, − i i h ud − i 2,1 2,1 2,1 = (,' k ) ,..., k ,..., )1 − k ,..., )1 − k ,..., 2,1 − i ,..., 2,1 = i i )1 k − )1 ' ' ' i i n y u i l i h ul ,' k k uh , ' k k i + 1 + ' 则由 或 ul , 1 1 uh , 1 1 ul ' ,' → 1 1 u ' ⇒→ 1 ul , ⇒ 2 uh , 2 2 2 →→ →→ 可求解 二、共轴光学系统的放大率 已知：1、各球面曲率半径 r1,r2,……rk 2、各表面顶点的间隔 d1, d2, ….. ,dk-1 3、折射率 n1, n2, ……, nk+1 讨论经共轴球面系统成像的几个光路计算问题。 1 βββ β k αααα k 1 γγγ γ k 2 2 = = = 2 1 且有 β = n 1 n ' k • k 2 ll l ' ' 1 l ll k 21 ' = un 11 un ' k k ' 并对整个系统有 ' β 2 1 β α = 1 n k n n 1 n k = γ = ' βαγ 三、光学系统的拉氏不变量 本章小结 由一个面的拉氏不变量 根据过渡公式得 j 1 = j j nyu = = 2 = = ——整个系统的拉氏不变量 ' uyn ' ' j j k = J表征了这个光学系统的性能，即能以多高的物、多大 孔径角的光线入射成像。J值大，表明系统能对物体成 像的范围大，成像的孔径角大，传输光能多。同时，孔 径角还与光学系统分辨微细结构的能力有关。 J值大的光学系统具有更高的性能 符号规则，在计算与有关推导中必须严格遵守 近轴光线经单个折（反）射球面的计算问题 单个折（反）射球面只对细小平面以细光束才能完善成像 焦距、光焦度、物距、像距、三种放大率 阿贝不变量，拉氏不变量（含义） 与本章内容有关的一些问题 精密球面面形测量，光学车间检验方法 3
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料