第 25 卷 第 12 期 文章编 号 : 100 1 ~ 5肠x( 2(X) 3 )12 一 1558 拱 系统工 程 与电 子技术 与吕t e lr 地 E 哈袱 n 嗯 a l训 D 忱加而cs Vo l . 25 , No . 12 , 五刃3 多 目标 优 化 设 计 中 的 P ar et o 遗 传 算法 ( 1 . 西北 工 业 大 学 , 陕 西 西 安 71 (X) 7 2 ; 2 . 上 海航 天 技 术研 究院 , 上 海 2 (X 犯33 ) 王 晓 鹏 ‘, 2 摘 要 : 遗传 算法 的 随机 性 和 隐含并行性 , 使 它 能 同时搜 索到多个局 部 最优 解并获得 最优 解集 。 为 了发挥遗 传 算法群体搜 索的优势 , 提 高 多 目标 优化设计效 率 和 灵 活性 在 自适 应 遗 传算 法的 基 础 上 引入群体排 序技术 、 小 生 境技 术和 R 此t o 解集过 滤 器 , 建立 了 一 种 适 用 于 多 目标优 化 设计 的 】恤祀t o 遗 传 算法 。 以 1〕are t o 前 沿 面 的形 式 给 出优 , 供设计 者按设计 意 愿选择最优 的设计 结 果 。 采 用 I、此t o 遗传 算法进 行跨声速翼 型 的 多 化 设计 的 几此t o 最优解集 目标优 化 设计 , 设计 结 果表明 , 几此t o 遗传 算法是 十分 有效 的 , 完 全 可 以 用 来进行 多 目标 优化 设计 。 , 关 健 词 : 遗传 算法 ; 多 目标 优化设计 ; 跨声速翼 型 中图 分类号 : 02 31 文献 标识 码 : A . obj P 恤代to g e n e 柱c al 卯ri 山m fo r m ul 廿 ec 廿v e O P 恤ul Za U0 n d es ign W A五G 兀盼pe ng l,2 八乞麟 “娜 化m Po 尔刻远必以 〔械诬忍邝ity , Xi’an 71 田72 , Ch 俪 ; ( ] . 旅 刀匆铂 云A〔浏翰l, of SI 润k 娜倒“ 了改五爪法卿 , 夕.少创妞点 2 田2 了3 , 日王拓切 2 . A h 由, d : 3 佣 h 珍6 c 田记 加p lic i 街 钾阳Ue l p ro pe rt l es o 拌in 过 朋 】m ion 咫卿哨笋t e . 玩 血晓r e ffi ec ti ve 即】u 石此 出日 。b 以in 皿叨训e tha obj 奴俪 明e 叽l 拌此t o 伍朋 w hj 目即‘吐叨 15 a p p li司 to 钾此勿 罗理 tic al g )ri c l e nC y 出 翻】口e x il〕i lity of m 』ti 一obj ‘tive o p ti 而 阳t io n des ign R 此t 。 罗n e tic is o 详in 止阳t ion 山呀ign , es 园dls 坛刃 1~ 」on se lf- 创la p tiv e 罗 11e tio fi lt e r are in 恢Klu e 找1. 1、此to so lu t ion set o P t i阳1 so luti on 娜男此ga t e e h des ign e 璐 n 旧y se lec t ~ sni 曰J e 叩6 而咖on des ign res u lts 二叨 五ng to c ax ry Out I n l l lt i 一obj ec t ive ae 喇恻丽 c o 口in l iZa tion ( Ies ign th m is e 压兄 t ive e n o u gh to 悦 ~ l in n l 己ti- obj ec 沈 。碑l邢 阳加n thn l ; m u lti 一obj eC t l v e j 跪ign ; 加u l so n lc a i而il of ge ll e b c al g o ri 俪 姗上e to e e l滋刃Iat it po ss il〕Ie the 即p l d a tion ~ h 印如田1峡卿 of al go ri th m , to ~ h for m 』6nle l以川 叩血川 g e ne tic 哑炯th m 山日 a ~ 能山记 如恤叹e for m 』ti . e he ni , al 邵们d m l wh ic h lx 〕即la tion 姗king tec 俪甲 e 11 曰y be the ir tr aJ 洲〕nic o p ti而 劝6 on des i gn . of p ro v 记洲」in the fo m 】 of inc lil u tion . R n 山y the ai rfo ih . 仆e des 妙 卫翅. l 知℃to 加n t l如℃ to 罗既tic sh o w Ul a t 枪 y 俐资 山 : 罗讹 t l c al 即ri 1 引 言 工程 实 际 中的许 多优化问题是 多 目标的优化设计问题 。 往往 通常情况 下多个 目标是处 于 冲突状态 的 , 不 存在一个最优设 计使所有的 目标同时达到最优 , 一个 目标性能 的改善 , 以其它 一 个或多个 目标性能 的降低 为代价 。 应 用 不同 的多 目标优化方法 , 对优化设计结果 的影 响很大 。 传统的多 目标 优化方法如加权组合法 、 目标 规划法 等 , 都是基 于 方向 搜索 需要导数信息 , 且容易收敛到局部最优解 ; 新兴 , 虽 然使用该方法进 起的模拟退 火方法是一 种随机搜索方法 行优化设计不 受 目标 函数性态的影 响 , 但也 只 能收敛到单个 最优点 , 所 以适用于 单 目标优化设计 。 而 遗传算法 的随机性 和 隐含并行性 , 使它能 同时搜索 到多个局 部最 优解 , 的优化方法 这对多 , , 无论 采用 自适应 遗传算法 目标优化是十分 有利 的 。 但是 ( SA( ;A ) 、 混 合 遗 传算 法 ( H以 ) 还 是其 它 在标 准遗 传 算法 ( SG A) 基础上经过改进的 遗传算 法 如果采用 加权组合 法 等 , 将多 目标转化为 单 目标的处理方法 就无法充分发挥遗传算 法 的优势 。 如果 把遗传 算法与 适用 于 多 目标 处理 的 几此协 , 方法 相 结合 , 就能完全 发挥遗传算法在多 目标优化设计 中的 作用 。 本文把 自适应 遗传算法 与 1恤此to 方法相结合 , 构 造出 适用 于 多 目标优化设计 的 Pare t o 遗传 算法 ( PG A ) , 并将其应 用 于跨声速翼型 的气动优化设计中 。 2 自适应 遗传算 法 标准遗传算法 t ’, 2 〕是 以二进制 为基础 的遗传算法 , 它采 用 赌盘选择方式和 单点遗 传操作 。 为 了 克服标准遗传算法 收 稿 日期 : 2 (X 犯 一 07 一 22 ; 修 回 日 期 二2 (X) 3 一 以 一 29 。 作 者简 介 : 王 晓鹏 (l 叭铸 一 ) , 男 , 副 教授 , 硕 士研 究 生 , 主要 研究 方 向为 可 靠性 数学 理 论 和随 机 最优 化 。 

第 12 期 多 目标优化设计中的 几此 t o 遗传算法 15 5 9 - 容易导致进化过程 中出 现过早 收敛和停滞现象等缺点 , 了多 种不 同版本的 自适 应遗 传算法 。 Sri M[ 操作 中的杂交概率 p 。 和 变异概率 几 3 〕。 根据各进化群 体 中适 应值 的分 布特点 动态 调 节 遗传 发展 v as M 和 几t n ai k L ni 瓜 〕 fave 瓜 < 赢 f 〕 fave < faw f ( l ) (2 ) 少耘 一 f 关涵 一 fate “k ; 式中 刁二‘- 个体 的 适应 值 , 适应值 , 续 k : 落 l ( i 二 l 儿— 两 个杂 交个体 中较 大的 几u 讥 忱— 当前 群体 的最大适 应值 和 平 均应值 , 0 , 2 , 3 , 4 ) 。 有的 自适 应遗传 算法 主要 是针对 变异操 作提 出的 。 它 在适应值排名选择的基础上采用 部分杂交 , 并较多地考虑到 , 认为较 合理的 搜索方式 变异算子 在遗传算 法中所起 的作用 应该是 : 适应值较大 的个 体在较小 的范 围 内搜索 , 适应 值较 小 的个体则应在较大的范围内搜 索 , 从而 构造 了以 下的 自适 应变异操作 : 设 {x ‘} 为执行变异 的父代个体 , 其 中分量 x * 发 生 变异 。若 x * 任 【a * , 则变异后 的 介 为 纵〕, x * + 公 ( T , b * 一 x * ) 套 = x * 一 乙( T , x * 一 a * ) 芬 = 式 中 : 夸— 从 O 和 1 中随机二选一的 结果 。 △ ( T , : ) = : ( l 一 ; 尹) 0 l (3 ) 户呱孤 。 式 中 : 一 【0 , 1 ] 上 的 随机 数 ; 几— 决定 一致性程 度的 参 数 , 一 般取值 为「2 , 5 」; 了- 变 异温度 , 其表达式为 T 二 l 本文把式( 3) 所述的 自适 应变异 操作 和 式 ( l ) 、 式 ( 2) 描 述的 自适应杂交概率和 变异概率 结合起来 , 将 形成 的 自适应 遗传算法作为 h 此 t o 遗传算法的基础 。 - 3 P . 限to 遗 传算法 在采用 P GA 处 理多 目标优 化 目标前 , 首先引人 h 此 t o 最 , 然后 简述 群体排 序 技术 、 小 生境 技术 和 R 此t o 优解 的概念 解集过滤器的具体操作 。 3 . 1 P . 陀t o 最优解 的概念 针对一般 的极小值问 题 m in gi ( X) J 、民to 最 优解的定义 , 对于 设计 变量组 X ‘ , 当且仅 为 : 在设计变量 的取值范 围 内 当不存 在其它 的设计 变量组 x , 在 不违 背约束 的 条 件下 满 足 : ( l ) 今 ( X ) 城 g ￡( X ’ ) ; < gi (2 ) 至 少 有 一 个 X 使 今 ( X ) 则设计变量组 x ’ 为 P a re t o 最优解 。 ( X ’ ) , , 对一个多 目标优化问 题而言 而是多个解 , , 其 1、沈 加 最优解 不是唯 一 并构成 P aJ 吧 t o 最 优解 集 。 在可 行解 集 中没 的 有比 R 此勿 最优解所对 应的个 体性能更 好的解 , 各 h 此t o 最 优解 之间也没 有优 劣之别 。 由于 P are to 最优解 集 中的任 何 解都可 能成为最优解 , 因而设计者可 以根据意愿 和对各 目标 0 最优 解集中选择出优化侧们聂满意的解 。 的重视程序 , 从 1知. 3 . 2 群体排序 技术 在应用 P GA 处 理 多 目标 问 题 时 , 各个 目标是 同等重要 的 , 并 没 有人为设定 各 目标 的权 重 , 所 以 待生 成 的 乃此 加 解 集中每个 h 此 t o 解都可 以作为最优解 它们 具有相 同的适应 值和 等级 。 以 下采用 群体排序技术确定 I 七A 中各个体 的适 应值 。 , 考虑某一 进化代中的 任意个体 X , 假设 群体中有 S 个个 体性能更优( 指各个 目标都有更优 良 的特性) , 则该个体 的等 级被确定为 1 十 S 。 由于 没有任何一个个体其性能会 比 h 此t o 解个体更优 , 所 以 1、此t o 解 的等级始终为 1 , 对 于其它个体 而 在群体中必然有更优 的个体 , 等级必然大 于 1 。 图 1 是上 , 在 图 中 , 标记 为 A 、 B 、 C 、 D 的个体等级分 , 言 述定级过程的图 示 别为 l 、2 、4 、6 。 确定 了进 化群 体 中各个 , 就 可 以 很 容 易 体的等 级 后 地确定各 个体 的适应 值 。 如 果群体中某个 体 的等级 为 ‘ , 则该个体 的 适应值 可 设 置为 1/ 、 。 这样 , 具有 P are t o 特性 的 个体 其 适 应值 最 大 而且 等 级越 高 的个 体 , 其 适 应值 越 小 。 可 见 , 处 于 同一 等 级 的 , _ _ _ _ _ _ ___ 裁裁 口 ::: : ___ _ 一一 月 万谊 { 耳 } 护 全 十 汤 一 一 丫丫 丫 飞 丫 一 一一 三 派 UUU ; 月 } _ !_ ___ … 全 ; 考考 疏 :一 口口 厂 i 护 犷犷 9 1闭 图 1 群 体排序 中的定 级 多个个体其适应值是相等的 3 . 3 小生 境技术 , 具有相 同的性能和 生存机会 。 基于 共享机制的 小生境技术闭 的基本思 想是 : 定义 共享 函数来确定每个少体在群体中的共享度 , 共享 函 数是关 于两 个体之间的关系密切程 序 ( 基因 型 或表 现型 的相 似性 ) 的 函 , 共享 数 。 个体间的 关系 比较密切时 函数值较小 。 基于 基因 型 的 共享函 数为 , 共享函 数值较 大 , 反 之 英如 比 ( X , Y ) = 0 1 一 a ( X , Y ) / 。撇 a ( x , y ) 妻 叮( X , Y ) a 撇 (4 ) < 叮 d 皿【 式 中 : 武 X , Y) — 任意两个不 同个体 X 和 Y 之间的欧 氏距 , 。 ‘, — 一个设定 的距离参数 , 几 眠 ( x , Y) —x 和 Y 的 离 共享 函数 。 引人共享 函数 的概念后 , 对群体中聚 集成小块的个体可 , 使其适 应值减小 , 从 而使 群 以通过施加共享 函数进 行惩罚 体 向具体 良好分布特 性的方 向进 化 。 施加共 享 函数后 个体 的适 应值 为 占( x ) 一、 = 一适工宜工一一 ( 艺几毗 ( X , zi ) 止二 l (5 ) ‘ n 式 中 : — 群体规模 , x — 群体中的任意个体 , Zi — 群 体中不同于 x 的 其它任意个体 , 创 x ) 和 叔 x )l 曲are 一 施加 共享函 数前后个体 X 的适应值 。 

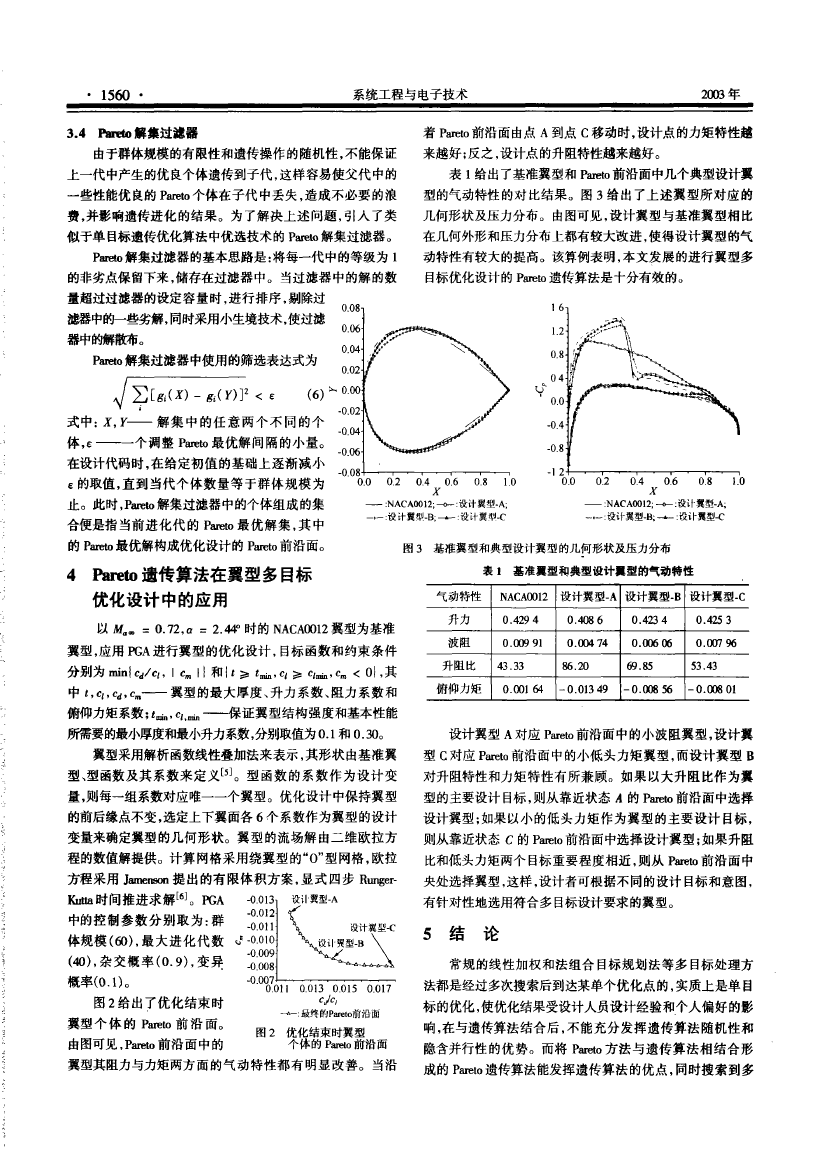
系统工程与电子技术 2 仪乃 年 着 P 毗t o 前沿 面 由点 A 到点 C 移动 时 来越好 ; 反 之 设计点的升阻特性越来越好 。 , , 设计点 的力矩特性越 表 1 给出 了基准翼型 和 几此加 前沿面 中几个典型设计翼 型 的气动特性 的对 比结果 。 图 3 给出 了上述翼 型 所对应 的 , 设计翼 型 与基准翼型 相 比 几何形状及 压力分布 。 由图 可见 , 使得 设计翼型 的气 本文发展 的 进行翼型 多 在几何外形 和 压力分布上 都有较大改进 动特性有较 大的提高 。 该算例表明 , 目标优化设计 的 R 此 t o 遗传算法 是十分有效的 。 l6l2 On0 40 场衅”00 护 0 石 0 8 1 0 0 _2 0 4 , 15 印 。 3. 4 几魄to 解集过滩器 由于群体规模 的有 限性和 遗传操作 的随机性 , 不能保证 这样容易使父代 中的 上一代中产生 的优 良个体遗传到子代 , 一些性能优良的 P 叮 d 。 个体在子代 中丢失 造成不 必要 的浪 费 , 并影响遗传 进化 的结果 。 为 了解 决上述 问题 , 引人 了 类 似于 单 目标遗传优化算法 中优选技术的 P 眠to 解集过滤器 。 巧川 。 解集过滤器的基本思路是 : 将每一 代中的等级为 1 的非劣点保 留下来 , 储存在过滤器 中 。 当过滤器中的解的 数 , , 进行排 序 , 剔除过 量超过过滤器的设定 容量时 滤器中的一些劣解 , 同时采用 小生境技术 , 使过滤 器中的解散布 。 巧此t o 解集过滤器 中使用 的筛选表达式为 006 1 了卢 。 当ZO ‘ UZ 未I ( 6 ) 卜 0 加 一0 . 0 2 一仓04 一O _ 06 一0 0 8 朴 0 . 0 0 2 0 . 4 , < 习 [ 二 ( x ) 一 二( Y) 」, 式 中 : x 冲 一 解 集 中 的任 意两 个不 同的 个 体 , 。 —一个调整 几此勿 最 优解间隔 的小量 。 , 在给定初 值的 基础 上 逐渐减 小 在设计代码 时 。 的取值 , 直 到当代个 体数量等 于 群体 规模 为 , h 此加 解集过滤器 中的个 体组成 的集 止 。 合便是指 当前进 化代 的 几此t o 最优解 集 , 其 中 的 h 此t o 最优解构成优化设计的 几此t o 前沿面 。 4 巧此to 遗传算法在翼 型 多 目标 此时 墓 孽 墓 撑 { 〕 { 襄 烧砍终张‘,班理誉”刃”‘议食华 亩合”吮泊”盏续袱呜呀一吸j孜户牛戈 优化 设 计 中的应 用 = 0 . 7 2 , 。 = 以 Ma . 2 . 440 时 的 NA c Aoo lZ 翼型 为基准 翼型 , 应用 P GA 进行翼型 的优化设计 , 目标 函数和 约束 条件 分别为 而n lcd / 白 , } 气 } } 和 I t 〕 t ~ , cl 蒸 c ,~ , 气 < 川 , 其 中 t 沟 , cd , ‘— 翼 型 的最大 厚度 、 升力系数 、 阻 力系数和 俯仰力矩系数 ; t ‘ , cl. ~ —保证翼 型结 构强 度和基本性能 1 和 0. 30 。 所需要的最小厚度和最小升力系数 , 湘 吐取值为 0. 翼型 采用 解析函数线性叠加法来表示 , 其形状 由基准翼 。 型 函 数 的系数 作 为设计 变 型 、型 函数 及其系 数来定 义[s] , 则 每一组系数对应唯一一个翼 型 。 优化设计 中保持翼型 量 选定上 下翼 面各 6 个系数作为翼 型 的设计 的前后缘点不变 , 变量来确定翼型 的几何形状 。 翼型 的流场解 由二维 欧拉方 “ O’ ’型 网格 , 欧拉 程的数值解提供 。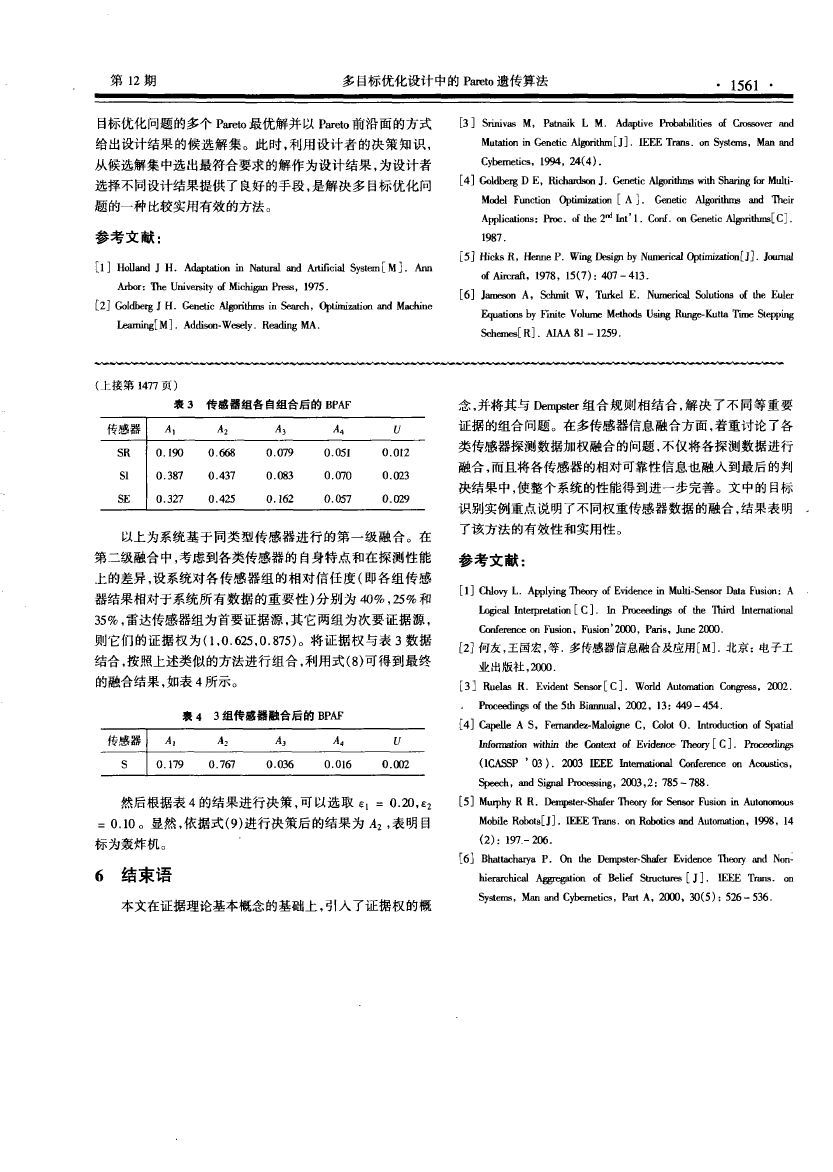 计 算网格采用 绕翼 型 的 方程 采 用 物脱~ 提出 的有 限体积 方案 , 显式 四 步 R u 飞 e r- K公tIa 时 间推进 求解[e] 中的控 制参 数 分别 取为 : 群 体规模 ( 印 ) , (40 ) , 杂交 概率 ( 0 . 9 ) , 概率(0 . 1 ) 。 一 0 刀13 一 0 12 一0 刀 1 1 一0 0 10 一0 t 0 0 9 一 0 0 0 8 一 0 0 0 7 最 大进 化 代数 设计 翼型 一A 。 P GA 变 异 才 0 0 1 1 0 刀 13 0 刀 15 0 . 0 17 图 2 给 出了 优化结束时 翼型 个 体 的 巧叨 t o 前 沿 面 。 由图可 见 , R 此t o 前沿面 中的 翼型其阻 力与力矩两方面 的气 动特性都 有 明显 改善 。 当沿 e 夕c 户 ~ : 最终 的Par 个体 的 I 恤况切 前沿 面 图 2 优化结 束时翼型 e to 前沿 面 — :N A C A 00 12; ~ : 设计翼 型 ·A; : 设计翼 型-C 一 十一 : 设 计翼型 X 一B; 一 0 6 0 名 1 . 0 X — :N ^c A oo lZ ;~ : 设计翼型一A ; 一一 : 设计 翼型 一B ;~ :设 计翼型( 图 3 基 准 翼型 和典 型设计翼 型 的几 何形状及 压 力 分布 表 1 基 准翼 型 和 典型 设 计皿型 的气动特性 气气 动特性性 N AC A(X) 1222 设计 翼型 一 AAA 设 计翼型一 BBB 设 计翼型 一CCC 升升 力力 波波阻阻 0 . 4 29 444 0 . 粼犯 666 0 . 收 3 444 0 . 礴2 5 333 0 . 以更) 9 111 0 . (X岭 科科 0 . 《】万 肠肠 0 . (】刀 肠肠 升升 阻 比比 43 . 3 333 86 . 2000 印 . 8555 53 . 4333 俯俯仰力 矩矩 0 . 00 1 研研 一 0 . 0 13 4999 一 0 . (】犯 5666 一 0 . (洲刃 0 111 设计翼 型 A 对应 Par e to 前沿面中的小波阻翼型 , 设 计冀 型 C 对应 P 眠 t o 前沿面 中的小低头力矩翼型 , 而设 计翼型 B 对升阻特性 和 力矩 特性有所兼顾 。 如 果以 大升 阻比作为翼 型 的主要设计 目标 , 则从靠近 状态 A 的 R 此勿 前沿面 中选择 设计翼型 ; 如果 以 小 的低头 力矩 作为翼型 的 主要 设计 目标 则从靠近 状态 C 的 1、re to 前沿 面中选择设计翼型 ; 如果升阻 则从 h 此勿 前沿面 中 这样 , 设计者可 根据不 同的设计 目标 和 意图 , 比和 低头力矩 两 个 目标重 要 程度相近 央处选择翼 型 , , , 有针对性地选用符合多 目标设计要求 的翼型 。 5 结 论 法都是经过多次搜索后 到达某单个优化点的 常规 的线性 加权和 法 组合 目标规划法等 多 目标处理方 , 实质上是单 目 标 的优化 , 使优化结果受设计人员设计经验和 个人偏好 的影 在与遗传算法 结合后 , 不 能充分发 挥遗传算法 随机性和 响 隐含 并行性 的 优 势 。 而将 巧此t o 方法 与遗传算 法相结 合形 成的 P a re t 。 遗传算法能发挥 遗传算法 的优点 , 同时搜索到多 , 

第 12 期 多 目标优化设计 中的 h 此t o 遗传算法 15 6 1 目标优化 问题 的多个 h 此t o 最优解并 以 1七re t l〕 前沿面 的 方式 利用 设 计者 的决策 知识 , 给出设计结果 的候选 解集 。 此 时 , 从候选解集 中选出最符合要求 的解作 为设计结果 , 选择不 同设计结果提供 了 良好 的手段 , 题 的一 种 比较实用有效 的方法 。 是解 决多 目标优 化问 为设计 者 [3 ] Sha iv as M , I , 曲】苗k L M . Ad a p l v 。 l 、先日司i t ies Mu 团。 in 《尧11eti 。 川, ‘uu 刀 [J] 场玩m e t i c s , 1望拜 , 24 (4 ) . . IE EE T r an s of C n ~ v er and . on 即st ~ , Man and [4 ] 。〕l山祀飞 D E , 凡 C h 盖坦‘价 J . C七n e t i e 月g 沽d m 班 初th 5 11如119 for M ul t i- M 斌妇e l F Un cti on OP ti ll ‘咖皿 [ A 」 A pp li c 川j o n s l 、阅 . of : . the Z 司 Int ’ 1 . Conf 晓n eti e 赶脚 健!切 巧 and Th e i r . on C七n e tic 川 g 示d u l 灼 〔C 〕 . 参考 文 献 : 19 87 , 儿 u l 〔5 」H i c k s R , H e n n e P . w i n g 兔咖 场 刊朋 祀 ‘阅 伽俪画on 〔J」 . Ji灿l 日 Of A i n 此改 , 19 78 , 15 (7 ) : 粼 )7 一 4 13 . 仁1 」H Oll and J H . Ad 即画二 in 入a t u r al and A rt 击ci al 即s tem [ M 〕 . 击场r : 肠e Uni 一ty of 陇chi 脚 P~ , I~ i嗯仁M 〕. 人山‘‘ 谓艘卜 〔2 」Gol dbe 电 J H . 晓n e l i c 川 g 耐 宜如E in 反肛c h , . R ea 庙 119 撇 197 5 . ( 、汕‘zat ion and M 歇」“Il e . L 接 第 14 77 页 ) 表 3 传感 器 组各 自 组合 后 的 B P A F 传感器 … , , SRsISE 0 . 1卯 0 . 肠8 0 . 3 87 0 . 3 27 4 37 0 . 42 5 A一‘‘rL 一0nU 一O了,J 0 . 162 A 4 0 . 0 5 1 m O 0 . 05 7 0 0 12 0 m 3 0 . 胆9 以上为系统基 于 同类 型 传感 器进 行的 第 一级 融合 。 在 第二级融合 中 , 考虑到各类传感 器的 自身特点 和 在探测 性能 上 的差异 , 设 系统对 各传感 器组 的相 对信任 度 ( 即 各组 传感 器结果相对于 系统所 有数据 的重要 性 ) 分别 为 4O % , 25 % 和 35 % , 雷达传感器组 为首要证据 源 , 其 它两组 为次要证 据源 , 则它 们的 证据 权为 ( 1 , 0 . 625 , 0 . 8 75) 。 将 证据权 与表 3 数据 按照上 述类似 的方法进行 组合 , 利用 式 ( 8) 可 得到最终 结合 , 的 融合结果 , 如表 4 所示 。 表 4 3 组传感 器 融合后 的 B l 〕AF 鹦糕六粉不念 A 。 0 . 0 16 U 0 . 田2 然后根据表 4 的结果进 行决策 , 可 以 选取 。 ; 二 0 . 20 , 。2 , 表 明 目 。 显然 , 依据式 ( 9) 进行决 策后的结果 为 A : = 0 . ro 标 为轰炸机 。 6 结束语 本文在证据理论基本概念 的基础 上 , 引 人了证 据权 的概 〔6 」J~ A , 阮lm 五t w , T 山rk e l E . Nu 脱ri te V o l山讹 M e dl ed s U s lng D 和a t i~ 坊 Fi ni S 如~ [ R 〕. A I AA 8 1 一 125 9 . e 目 阮l u t~ of Rl in g e ~ K u t ta Ti n 祀 S 沈p p哩 E ll ler the 念 , 并将其与 De m ps t e r 组 合规 则相结 合 , 解决 了 不 同等重 要 证据的组合 问题 。 在 多传感器信息融合方 面 , 着重讨论 了各 类 传感 器探测数据加权融合 的问题 , 不 仅将各探测数据进行 融合 , 而且将各传感器的相 对可靠性信 息也融入到最后 的判 决结果 中 , 使整个系统的性 能得到进一步完善 。 文 中的 目标 识别实例重点说 明了不 同权重传感器数据 的融 合 , 结果 表 明 了该方法 的 有效性 和 实用性 。 参考 文 献 : [l 〕C日0 叮 L . A pp 甲ng Th 。叮 of Evi L 〕gi 祖 玩抚印 r e ta tion 〔C 〕 O 川企此n e e on Fu s ion , Fu si on , 2 (X X) In . d e n c 。 in M u l 性i一 p ” x 默月哪 of l 〕at 骊sor th e Th in l , P 而s , 」明e Z(X X) . a Fu si on : A lnt ~ i o n al 【2 」何友 , 王 国 宏 , 等 业 出版社 , 2(X 幻 . . 多 传感 器 信息 融 合及 应 用 〔M 〕 . 北 京 : 电 子 工 [ 3 〕R u e las R . E vi den t Se n so r [ C 〕 . W 6r ld A u 奴姐l 以 ion C O n 邵仑SS , 勿以〕2 . R 仪喇in 乎 of the s th Bi 田m u 司 , 2(X 犯, 13 : 科9 一 454 . 仁41 0 叼祀ll e A S , F e m an d e Z 一耐oi 脚 C , 肠!。t 0 . In tr 以Iu c t i二 of 5 1犯Iial of b 扬 n l 班主i二 衍 山i n 阮 C 加ltext (I C配弱P ’ 03 ) . 称~ h , 朋d si 罗 al . 乃议三川坛卿 2 (X) 3 I EE E In t e m 出 j田司 O 用屁r e n e e 二 人( 朋泌c8 , p 脱麟ing , 2 (X )3 , 2 : 78 5 一 7 88 . E 、记即, 仆仪叮 〔C 〕 了 【5] Mu 印hy R R . 块 ”样 ter- Sh 司Fe r Th 印 ry IE E E T n ”15 . on RD Ix 石cs an d A u t O l l 坦t ion , 1卯8 , 14 for 反 n so r Fu si on in An t~ s . Mo bile R o l刃t s 【J] (2 ) : 197 一 2肠 . 仁6 」Bl l at hi t 朋 11田 手a P . On the De n 甲~ S h 司re r Evi e ~ hi A 婴{件到ion of Be li ef 勿s l e n ‘ , Man an 《1 Cy l祀m e l e s , 1〕axt c al d e n c e Th 印ry and Non- on I EE E T 皿l s . St 川C 加找毖 【J 〕. A , 2‘XX ) , 30 (5 ) : 5 26 一 53 6 .