logo资料库

考虑终端角度约束的自适应积分滑模制导律.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.64M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    第 32 卷 第 11 期 2017 年 11月 控 制 与 决 策 and Decision Control Vol.32 No.11 Nov. 2017 文章编号: 1001-0920(2017)11-1966-07 DOI: 10.13195/j.kzyjc.2016.1167 考虑终端角度约束的自适应积分滑模制导律 赵 斌1y, 周 军1, 卢晓东1, 李 烨2 (1. 西北工业大学 航天学院，西安 710072；2. 中国运载火箭技术研究院 战术武器事业部，北京 100076) 文献标志码: A 摘 要: 针对机动目标拦截末制导问题, 提出一种考虑终端角度约束的自适应积分滑模制导律. 首先给出一种有 限时间收敛的非线性积分滑模面, 采用快速终端滑模设计趋近律; 然后设计一种对目标机动加速度上界平方进行 估计的自适应律, 给出具有光滑特性的自适应积分滑模制导律; 最后基于有限时间理论证明闭环系统的有限时间 收敛特性, 并给出滑模变量、视线角以及视线角速率的收敛域. 数值仿真结果验证了所提出设计方案的有效性. 关键词: 终端角约束；有限时间收敛；积分滑模；自适应制导律；机动目标；齐次理论 中图分类号: V448.13 Adaptive integral sliding mode guidance law considering impact angel constraint ZHAO Bin1y, ZHOU Jun1, LU Xiao-dong1, LI Ye2 (1. School of Astronautics，Northwestern Polytechnical University，Xi’an 710072，China；2. Tactical Weapons Division， China Academy of Launch Vehicle Technology，Beijing 100076，China) Abstract: An adaptive integral sliding mode guidance law with impact angel constraint is proposed for the guidance problem during the maeuvering target interception. Firstly, the nonlinear integral sliding manifold with finite time convergence is designed and the reaching law is given based on the fast terminal sliding mode. Secondly, an adaptive law is proposed to estimate the square of the target maneuvering acceleration bound, based on which the adaptive integral sliding mode guidance law is derived, which possesses the smooth feature. Finally, the finite time convergence of the guidance system both for the reaching phase and on the sliding mold is proved based on the finite stability theory, and the convergence regions of the sliding variable and the system states are derived. Simulation results show the effectiveness of the proposed method. Keywords: impact angle constraint；finite time convergence；integral sliding mode；adaptive guidance law；maneuvering target；homogeneous theory 0 引 战术导弹末制导律的作用是导引导弹精确命中 目标. 随着技术的发展, 来袭目标速度越来越高, 同时 具有一定的机动能力,这要求导弹不仅能够准确命中 目标,而且要以特定的攻击角度命中目标以充分发挥 战斗部的毁伤效能. 因此, 具有终端攻击角度约束的 制导律成为目前研究的热点. 该领域的早期研究大都基于比例导引的改进方 法进行角度约束制导律设计. 文献 [1-2] 在比例导引 的基础上增加修正项,实现了对目标机动的补偿以及 期望的终端角度约束; 文献 [3-4] 通过实时改变比例 导引的导航比增益分别实现了对静止目标和非机动 目标的拦截. 然而, 在针对大机动目标拦截时, 这些方 法由于缺少目标运动信息会导致拦截精度难以保证. 滑模变结构控制[5] 对于匹配条件下的外部干扰 和模型不确定具有不变性,近年来已广泛应用于制导 律的研究中. 文献[6] 给出了应对机动目标的自适应 滑模制导律,所采用的线性滑模使得视线角速率收敛 时间无穷大, 此外其假设目标机动加速度上界已知, 这在非合作目标拦截时无法获取. 这两点不足使该 方法无法用于机动目标的拦截. 因此, 有限时间控制 方法与具有干扰估计特性的自适应方法相结合成为 解决以上问题的主要思路. 在有限时间控制方面, 文献[7] 提出了终端滑模 收稿日期: 2016-09-13；修回日期: 2017-02-08. 基金项目: 国家863 计划项目(2015AAxxx7033, 2015AAxxx1008)；航天支撑基金项目(2015-HT-XGD). 作者简介: 赵斌 (1986), 男, 讲师, 博士, 从事先进控制理论及飞行器精确制导与控制的研究；周军 (1966), 男, 教 授, 博士生导师, 从事飞行器制导与控制理论等研究. 通讯作者. E-mail: binzhao@nwpu.edu.cn y
    第11期 赵 斌 等: 考虑终端角度约束的自适应积分滑模制导律 _r = Vt cos(q t) Vm cos(q m); r _q = Vt sin(q t) + Vm sin(q m); _t = At/Vt ; _m = Am/Vm: 1967 (1) (2) (3) 控制, 通过引入非线性滑模面, 在理论上保证了状态 的有限时间收敛特性. 文献[8-10] 提出的角度约束终 端滑模制导律能够实现视线角速率及视线角的有限 时间收敛. 然而, 当系统状态远离原点时, 其收敛速度 相比线性滑模更慢, 这对短暂的末制导过程很不利. 文献[11] 通过在终端滑模中引入线性滑模项有效解 决了此问题,该方法同样被用于终端角度约束制导律 设计[12-13]. 然而, 这两种制导律由于存在状态量的负 指数项而导致奇异问题. 目前解决思路有两种, 其一 是采用非奇异的终端滑模及快速终端滑模[14-15]; 其 二是采用积分滑模[16]. 这两种方法都已经用于制导 律的研究[17-20]. 应对目标机动干扰的研究思路有3 种: 第一是采 用干扰观测器实现对系统不确定性的在线估计[21-22]; 第 二 是 基 于 自 适 应 律 实 现 对 目 标 干 扰 上 界 的 估 计[17-18]; 第三是在设计过程中不考虑目标机动, 通过 稳定性理论证明系统的稳定[6,19,23]. 这些方法的共同 问题是引入了滑模变量的符号项,导致制导律不连续 而引起震颤问题,若采用连续光滑的函数近似替代符 号函数,则会牺牲系统的控制精度. 针对有限时间制导律设计中存在的奇异和非光 滑问题,本文提出一种基于自适应滑模控制的终端角 度约束制导律. 首先基于齐次理论设计满足有限时 间收敛的积分滑模, 有效解决奇异问题; 然后提出一 种新的估计目标机动加速度上界平方的自适应律,避 免引入符号项, 解决非光滑问题; 最后基于有限时间 稳定理论证明整个系统在可达阶段和滑模阶段的有 限时间收敛特性. 1 数学建模 将目标和导弹视为质点,二维场景下的弹目相对 运动关系如图1所示. 图 1 二维弹目相对关系 图1 中: M 和 T 分别是导弹和目标; Vm 和 Vt 分别 是导弹和目标的速度; Am 和 At 分别是导弹和目标的 加速度, 其方向与速度方向垂直; r 是弹目相对距离; q 是视线角; m 和 t 分别是导弹和目标的航迹角. 由 此,可以建立非线性弹目相对运动方程[22] 如下: 不失一般性,在进行系统设计时作如下假设. 假设1 忽略导弹自动驾驶仪和导引头的动态 假设2 目标加速度及其微分均有界, 即jAtj ⩽ 特性,即认为弹体可以理想实现制导过程. dt1,j _Atj ⩽ dt2, dt1、dt2 为未知的正常数. 假设3 在短暂的末制导过程中, 假设导弹与目 标速度大小不变. 假设4 末制导过程中弹目相对距离不断减小, 即 _r(t) < 0, 0 < r(t) < r(t0), t0 < t < te, t0 和 te 分别 为末制导的起止时刻. 对式(2)求导并代入式(1)和(3),可得 2 _q _r r At cos(q t) Am cos(q m) + r r q = : (4) 定义末制导的终端角 (te) 为命中瞬间导弹与目 标速度方向的夹角, 该角度与终端弹目视线角 q(te) 存在一一对应关系[22],即 q(te) = t tan1 sin (te) ) ( (5) : cos (te) Vt/Vm 因此, 攻击角约束问题便可转化为终端视线角 q(te) = qd 的约束问题. 由假设3 可知, 式(5) 中的第2 项为 常数, 若选状态变量 x1 = q qd; x2 = _x1, 则可将式 (4)表述为如下状态方程: 2 _r r 8<: _x1 = x2; 其中: f = At cos(q t) r _At/Vt 2 _rAt/Vt 表征 由未知且有界的目标机动加速度引起的干扰项,由假 设 2 可知其满足jfj ⩽ dm, dm 为未知的干扰上界; u = Am cos(q m)为待设计的制导指令. x2 u _x2 = (6) f r + r : 本文的目标是设计自适应且光滑的制导律 u, 使 得在未知干扰 f 存在的情况下, 式 (6) 中的系统状态 有限时间收敛至零. 2 制导律设计 2.1 相关引理及定义 首先给出制导律推导需要的引理及定义. 引理1 [14] 定义在原点邻域 U Rn 上的 C 1 光 滑正定函数 V (t), 若存在实数 a; b > 0; 0 < < 1, 使 得下式成立: _V (t) + aV (t) + bV (t) < 0; (7) 其中t > t0; t0 是系统运行的初始时刻,则该函数将在 有限时间收敛至零,且收敛时间满足 te ⩽ t0 + 1 a(1 ) ln aV 1(t0) + b : (8) b AtVtVmAmγmrTqqγtM
    1968 控 制 与 决 策 第32卷 ) s + jsjsgn s + ^kd1s (18) 注1 式 (18) 不含有状态的负指数项及非光滑 : (9) 的符号项,因此该制导律是非奇异且光滑的. 引理2 [24] 对于实数 m; n ⩾ 0; p; q > 1, 若其满 足等式1/p + 1/q = 1,则如下不等式成立: mn ⩽ 1 p mp + 1 q nq: 引理3 [25] 对于r 重积分链式系统 _y1 = y2; _yr1 = yr; _yr = u: ; 若∆(p) = pr + krpr1 + + k2p + k1 是Hurwitz多 项式,且k1; k2; ; kr > 0,则下式所示的状态反馈控 制可使该系统有限时间镇定: u = k1jy1j1sgn y1 krjyrjrsgn yr: (10) 其中参数i 满足 ; i = 2; 3; ; r; ii+1 2i+1 i i1 = r+1 = 1; r = ; " 2 (0; 1); 2 (1 "; 1): (11) 定义1 [19] 平均拦截加速度 AME 定义为制导律 加速度指令绝对值的数学期望 AME = 1 N jAm(k)j: (12) N∑ k=1 其中: Am(k) 为第 k 步制导律 Am 的计算值, N 为总的 仿真步数. 2.2 自适应积分滑模制导律设计 s = x2 + 针对系统(6)设计如下的积分滑模: t 0 (k1jx1j1sgn x1 + k2jx2j2sgn x2)dt; (13) w 其中相关参数取值满足引理3要求,即 1 = 23 23 2 " 2 (0; 1); 2 (1 "; 1); ; 2 = ; 3 = 1; 且k1; k2 > 0满足Hurwitz条件. 对式(13)求导并代入系统方程(6),可得 _s = k1jx1j1sgn x1 + k2jx2j2sgn x2+ 2 _r r x2 u r + f r : (14) (15) (2 _r 若选择如下快速终端滑模进行趋近律设计: _s = s jsjsgn s; ; > 0; 0 < < 1: ) 则由式(14)和(15)可得制导律表达式为 r u = r s + jsjsgn s + x2 + k1jx1j1sgn x1 + k2jx2j2sgn x2+ (16) 式(16) 中含有的未知干扰项 f 使其无法应用, 需要增 加自适应项. 为消除已有自适应律引入的不连续符 号项, 本文提出一种对目标干扰上界的平方 k = d2 m 进行估计的自适应律,其表达式如下: f r : _^k = d1(s2 d2 ^k); d1; d2 > 0: (17) 给出自适应积分滑模制导律(AISMGL)为 u = r x2 + k1jx1j1sgn x1 + k2jx2j2sgn x2+ (2 _r r ) 1 1 ( ∆ k1 定理1 对于式(6)所描述的系统,若设计滑模面 和趋近律分别为式(13) 和(15), 自适应律和制导律分 别为(17)和(18),则如下结论成立: 1) 滑模变量有限时间收敛于jsj ⩽ ∆1; 2) 状态有限时间收敛于jx1j ⩽ ∆3 和jx2j ⩽ ∆2. ) 1 ( 各个收敛域表达式如下: ∆1 = (1/4d1rte 1 2 ) +1 ; ∆2 = ∆ k2 2 ; ∆3 = ; ∆ = 1∆1 + 1∆1 1 : (19) 证明 该定理证明过程可分为3步完成. Step 1 证明干扰的估计误差有界. 对式(13)求导,并代入式(6)和(18),可得 s2 jsj+1 ^kd1s2: (20) 定义自适应律的估计误差为 ~k = k ^k, 并选择 f s r s _s = Lyapunov函数为 V = ~k2 + s2: (21) 1 2 1 2 对该式求导并代入式(17)和(20),可得 _^k = _V = s _s ~k f s r s2 jsj+1 kd1s2 + ~kd1d2 ^k: (22) 由于jfj ⩽ dm; jsj+1 > 0,上式可缩放为 kd1s2 + d1d2k~k d1d2 _V ⩽ s2 + dmjsj r 由引理2可知,当p = 2; q = 2时,有 p mn; m; n ⩾ 0: m + n ⩾ 2 据此可知如下不等式成立: √ 1 ⩾ 2 4d1r2 kd1s2 4d1r2 = dmjsj r ; 8>><>>:kd1s2 + (k2 + ~k2) ⩾ jk~kj ⩾ k~k: 1 2 将式(25)代入(23),可得如下不等式成立: _V ⩽ s2 + V + : d1d2k2 1 4d1r2 + d1d2 1 2 1 2 ~k2 ⩽ (26) 1 其中: = minf2; d1d2g; = d1d2k2. 由 参数范围可知 ; > 0. 当 V > / 时, _V < 0 成立, 因此 V 大小有界,滑模变量 s与估计误差 ~k 有界. 可令 j~kj ⩽ , 是未知的正常数. 4d1r2 + 1 2 Step 2 证明滑模变量的有限时间收敛. 重新选择Lyapunov函数为 ~k2: (23) (24) (25)
    第11期 赵 斌 等: 考虑终端角度约束的自适应积分滑模制导律 1969 ′ V = s2/2: (27) _s jx2j2sgn x2 . 由式(35) 可知, 当 2 2 (1 ; 1); 1 = 2 2 2 时, 由引理3 可知系统在滑模面上的运动有限时间收 敛的充分条件为 k 1; k2 组成的多项式 满足Hurwitz条件. 因此 1 > 0, 此时 k ′ ′ jx1j ⩽ ) 1 ) 1 (j _sj (j _sj k1 k2 1 ⩽ 2 ⩽ 1 ) 1 ) 1 2 ( ( ∆ k1 ∆ k2 同理,由式(36)可得x2 的收敛域如下: = ∆3: (37) = ∆2: (38) jx2j ⩽ 证明成立.2 3 数学仿真 对其求导,并代入式(20)和(25),可得如下不等式: 4d1r2 = _V ′ ⩽ s2 jsj1+1 + d1s2 + 1 V ′ V ′ ; 其中: = 2( d1); = 2 1 4d1r2jsj+1 + 1 2 . 分情况讨论如下: 1) 当x2 ̸= 0时,若选择参数满足以下条件: ( 8><>: > d1; > 1 4d1r2jsj+1 ; ) (28) , = (29) 则式(28) 中 ; > 0; 0 < < 1, 由引理1 可知此时 系统满足有限时间收敛. 2) 当 x2 = 0 且 s ̸= 0 时, 将控制器(18) 代入系统 方程(6)的第2式,可得 _x2 = f r s jsjsgn s ^kd1s k1jx1j1sgn x1 k2jx2j2sgn x2: (30) 考虑到积分滑模面的定义, 上式无法确保 _x2 = 0, 即 x2 = 0不是系统滑模到达阶段的吸引子,因此滑模变 量可在有限时间内收敛至零. 3) 当系统到达滑模面时,由积分滑模定义可知 _s = _x2 + k1jx1j1sgn x1 + k2jx2j2sgn x2 = 0: (31) 该式满足引理3 条件, 因此处于滑模面上的系统状态 x1 和x2 将在有限时间内收敛至零. Step 3 给出状态变量的收敛域. 式(29) 给出了滑模到达阶段有限时间收敛的条 ( ) 1 ( 件,据此可知滑模变量收敛域如下: jsj < = +1 1 1 4d1r2 4d1rte 2 ) 1 +1 = ∆1: (32) 由式(15)和(32)可知 j _sj ⩽ 1jsj + 1jsj1 = 1∆1 + 1∆1 对积分滑模面(13)求导,可得 _s = _x2 + k1jx1j1sgn x1 + k2jx2j2sgn x2: 1 = ∆: (33) (34) 该式可以改写为如下两种形式: _x2 + k1 _x2 + k1jx1j1sgn x1 + k ′jx1j1sgn x1 + k2jx2j2sgn x2 = 0; 2jx2j2sgn x2 = 0: ′ 其 中: k ′ 1 = k1 _s jx1j1sgn x1 ′ ; k (35) (36) 2 = k2 本节通过数学仿真对上述算法进行验证,算法的 总体结构如图2 所示, 其中用到的制导参数见表1, 初 始仿真场景见表2, 仿真周期选择为1 ms, 过载限幅为 40 g. 图 2 自适应积分滑模制导律结构框图 表 1 积分自适应积分滑模制导律参数 k1 k2 1 2 d1 d2 qd / deg 0.4 0.84 0.538 5 0.7 0.8 20 0.5 100 0.001 20 表 2 导弹与目标初始条件 x(0) y(0) (0) V (0) Missile 0 m 0 m ◦ 60 600 m/s Target p 2 500 3 m 2 500 m ◦ 0 300 m/s 选择以下典型目标运动形式进行仿真验证. 场景1:正弦机动, At = 7g cos(t/4) m/s2. 场景2:常值机动, At = 7g m/s2. 场景3:方波机动,加速度为 8<:At = 7g m/s2; t < 5 s; At = 7g m/s2; t ⩾ 5 s: 表 3 仿真结果 Scenario 1 Scenario 2 Scenario 3 AISMGL NTSMG1 NTSMG2 AISMGL NTSMG1 NTSMG2 AISMGL NTSMG1 NTSMG2 Interception Time / s Miss Distance / m AME / (m/s)2 16.097 0.017 80.789 5 17.774 0.067 18.602 0.136 128.967 2 158.907 9 15.200 0.161 73.377 2 15.769 0.254 16.027 0.060 140.229 3 174.047 0 11.704 0.277 65.921 4 12.092 0.289 12.282 0.294 155.934 0 196.942 9 L᪗ʡ4ɂᜮ?ɂQᵫ4᪀Oᑖɂ(13)xx12,L᪗ʡ4Q〉(17)Q〉Oᑖᑴ18)(ʣYqds
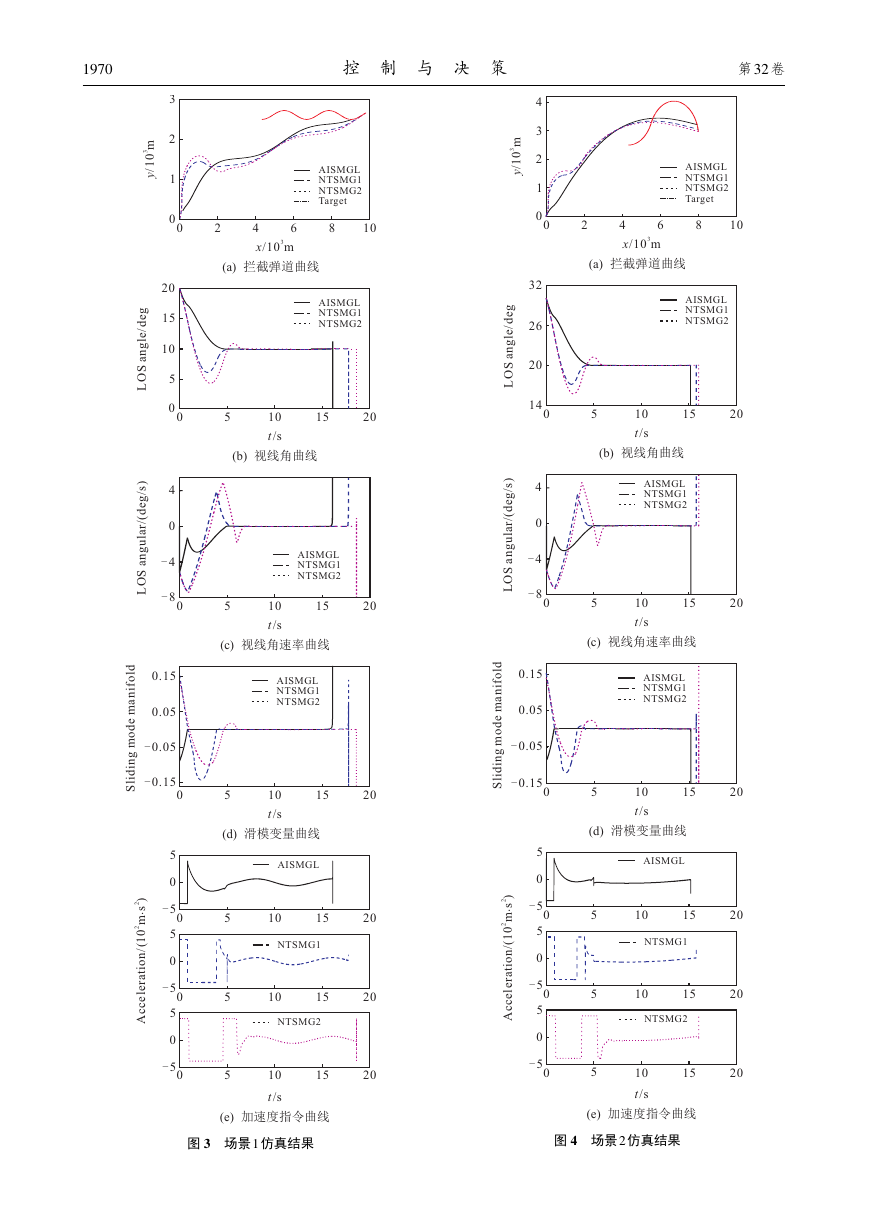
    1970 控 制 与 决 策 第32卷 图 3 场景1 仿真结果 图 4 场景2 仿真结果 0246810x/10m3(a)>ɮ⍝B05101520t/s(b)YYB(c)YY΅᳛B(d)5[B(e)4΅ᢣB0123y/10m3AISMGLNTSMG1NTSMG2Target05101520LOS angle/degAISMGLNTSMG1NTSMG205101520LOS angular/(deg/s)-8-404t/st/s05101520-0.15-0.050.050.15AISMGLNTSMG1NTSMG2AISMGLNTSMG1NTSMG2Sliding mode manifold05101520-55005101520-55005101520-550AISMGLNTSMG1NTSMG2t/sAcceleration/(10m.s22)0246810x/10m3(a)>ɮ⍝B05101520t/s(b)YYB(c)YY΅᳛B(d)5[B(e)4΅ᢣB0124y/10m3AISMGLNTSMG1NTSMG2Target14202632LOS angle/degAISMGLNTSMG1NTSMG205101520LOS angular/(deg/s)-8-404t/st/s05101520-0.15-0.050.050.15AISMGLNTSMG1NTSMG2AISMGLNTSMG1NTSMG2Sliding mode manifold05101520-55005101520-55005101520-550NTSMG1NTSMG2t/sAcceleration/(10m.s22)3AISMGL
    第11期 赵 斌 等: 考虑终端角度约束的自适应积分滑模制导律 1971 为了客观评价本文算法的性能, 在同样的场景 及初始条件下对于文献[17-18] 的两种自适应非奇异 制导律(分别记为NTSMG1 和NTSMG2) 也进行了仿 真. 仿真结果对比如图3 图5所示,相关结果总结于 表3中,据此可以得到如下结论: 1) 从3 种场景的二维弹道曲线可以看出, 本文提 出的自适应滑模制导律所产生的攻击弹道最平直,且 命中目标最早. 从表3 中的拦截时刻也可以得到同样 结论. 2) 从图 3 图 5 所示的视线角曲线可以看出, 3 种方法都可以保证视线角有限时间收敛于指定 的 终 端 角, 本 文 算 法 作 用 下 视 线 角 的 收 敛 时 间 与 NTSMG1 相当, 比NTSMG2 更快, 且在收敛过程中视 线角没有出现过零的振荡现象. 3) 从图3 图5 所示的视线角速率曲线可以看 出, 3种方法都能保证视线角速率有限时间收敛,相比 之下, NTSMG1和NTSMG2存在明显的尖峰现象. 4) 从图3 图5 所示的滑模变量曲线可以看出, 本文的方法由于采用快速终端滑模进行趋近律设计, 其滑模可达阶段的收敛速度最快, 且不存在过零震 荡,这是其弹道最平滑的主要原因. 5) 从图3 图5 所示的制导指令曲线可以看出, 本文方法产生的制导指令饱和时间最短, 且完全光 滑, NTSMG1 和NTSMG2 由于要抑制视线角速率两 次严重的尖峰现象, 因而饱和时间更长, 这使得本文 方法产生的平均拦截加速度在3 个场景下都是最小, 如表3所示. 6) 由表3 可知, 本文提出的制导律除了是非奇异 且光滑外, 主要的优点是拦截时间更短, 拦截精度更 高,且需要的平均拦截加速度更小. 4 结 论 本文基于自适应积分滑模控制提出了一种考虑 终端角度约束的非奇异光滑制导律,并通过多场景仿 真对算法进行了验证,相关结论如下: 1) 基于齐次理论设计积分滑模面,可以确保系统 状态在滑模面上的有限时间收敛特性; 2) 基于快速终端滑模设计趋近律,可以确保系统 滑模变量在可达阶段的有限时间收敛; 3) 针对目标未知机动引起的不确定干扰,采用本 文提出的对干扰上界平方进行估计的自适应律,可以 从根本上避免由非光滑符号函数引起的震颤问题; 4) 在同样的场景下,本文制导律实现的拦截时间 更早、脱靶量更小, 而且过载指令光滑、饱和时间更 短,平均拦截加速度更小. 图 5 场景3 仿真结果 0246x/10m3(a)>ɮ⍝B051015t/s(b)YYB(c)YY΅᳛B(d)5[B(e)4΅ᢣB0125y/10m3AISMGLNTSMG1NTSMG2Target14202632LOS angle/degAISMGLNTSMG1NTSMG2LOS angular/(deg/s)-8-404t/st/s-0.15-0.050.050.15AISMGLNTSMG1NTSMG2AISMGLNTSMG1NTSMG2Sliding mode manifold-550-550-550NTSMG1NTSMG2t/sAcceleration/(10m.s22)3AISMGL40510158051015051015051015051015
    1972 参考文献(References) 控 制 与 决 策 第32卷 [1] Kim B S, Lee J G, Han H S. Biased PNG law for impact with angular constraint[J]. IEEE Trans on Aerospace and Electronics Systems, 1998, 34(1): 277-288. Erer K S, Merttopcuoglu O. Indirect impact-angle control against stationary targets using biased pure proportional navigation[J]. J of Guidance, Control, and Dynamics, 2012, 35(2): 700-704. [2] [3] Ratnoo A, Ghose D. constrained interception for stationary targets[J]. J of Guidance, Control, and Dynamics, 2008, 31(6): 1816-1821. Impact angle [4] Ratnoo A, Ghose D. Impact angle constrained guidance against nonstationary nonmaneuvering targets[J]. J of Guidance, Control, and Dynamics, 2010, 33(1): 269-275. [5] Utkin V I. Variable structure system with sliding modes[J]. IEEE Trans on Automatic Control, 1977, 21(2): 212-222. Zhou D, Mu C D, Xu W L. Adaptive sliding mode guidance of a homing missile[J]. J of Guidance, Control, and Dynamics, 1999, 22(4): 589-594. [6] [7] Man Z H, Paplinsky A P, Wu H R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators[J]. IEEE Trans on Automatic Control, 1994, 39(12): 2464-2469. [8] Kumar S R, Rao S, Ghose D. Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints[J]. J of Guidance, Control, and Dynamics, 2012, 35(4): 1230-1246. [9] He S M, Lin D F. A robust impact angle constraint guidance law with seeker’s field-of-view limit[J]. Trans of the Institute of Measurement and Control, 2015, 37(3): 317-328. [10] Zhang Y X, Sun M W, Chen Z Q. Finite time convergent guidance law with impact angle constraints based on sliding mode control[J]. Nonlinear Dynamics, 2012, 70(1): 619-625. [11] Yu X H, Man Z H. Fast terminal sliding mode control design of nonlinear dynamics systems[J]. IEEE Trans on Circuit and Systems I: Fundamental Theory and Applications, 2002, 49(2): 261-264. [12] Golestani M, Vali A R, Najjari S, et al. Finite-time convergence of guidance system via fast terminal sliding mode control[C]. Proc of the 23rd Iranian Conf on Electrical Engineering. 2015: 899-904. [13] Song J H, Song S M, Guo Y, et al. Nonlinear disturbance observer-based fast terminal sliding mode guidance law with impact angle constraints[J]. Int J of Innovative Computing, Information and Control, 2015, 11(3): 787-802. [14] Yu S H, Yu X H, Shirinzadeh B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964. [15] Liang Y, Yang J Y. Nonsingular fast terminal sliding mode control for nonlinear dynamical systems[J]. Int J of Robust and Nonlinear Control, 2011, 21(16): 1865-1879. [16] Zong Q, Zhao Z S, Zhang J. Higher order sliding mode control with self-tuning law based on integral sliding mode[J]. IET Control Theory and Application, 2008, 4(7): 1282-1289. [17] Song J H, Song S M, Zhou H B. Adaptive nonsingular fast terminal sliding mode guidance law with impact angle constraints[J]. Int J of Control, Automation and Systems, 2016, 14(1): 99-114. [18] He S M, Lin D F. Adaptive nonsingular sliding mode based guidance law with terminal angular constraint[J]. Int J of Aeronautical and Space Sciences, 2014, 15(2): 146-152. [19] 熊少锋, 王卫红, 王森. 带攻击角度约束的非奇异快 速终端滑模制导律[J]. 控制理论与应用, 2014, 31(3): 269-278. (Xiong S F, Wang W H, Wang S. Nonsingular fast terminal sliding-mode guidance with interception angle constraint[J]. Control Theory & Applications, 2014, 31(3): 269-278.) [20] Song J H, Song S M. Three-dimensional guidance law based on adaptive integral sliding mode control[J]. Chinese J of Aeronautics, 2016, 29: 202–214. [21] 王晓芳, 郑艺裕, 林海. 基于扰动观测器的终端角约 束滑模导引律[J]. 系统工程与电子技术, 2014, 36(1): 111-116. (Wang X F, Zheng Y Y, Lin H. Sliding mode guidance law with impact angle constraint based on disturbance observer[J]. Systems Engineering and Electronics, 2014, 36(1): 111-116.) [22] Wang W H, Xiong S F, Liu X D, et al. Adaptive nonsingular terminal sliding mode guidance law against maneuvering targets with impact angle constraint[J]. Proc of the Institution of Mechanical Engineers, Part G: J of Aerospace Engineering, 2015, 229(5): 867-890. [23] Zhang Y X, Sun M W, Chen Z Q. Finite-time convergent guidance law with impact angle constraint based on sliding-mode control[J]. Nonlinear Dynamics, 2012, 70: 619–625. [24] Sun C Y, Feng C B. Exponential periodicity and stability of delays neural networks[J]. Mathematics and Computers in Simulation, 2004, 66(5): 469-478. [25] Bhat S, Bernstein D. Geometric homogeneity with applications to finite time stability[J]. Mathematics of Control Signals and Systems, 2005, 17(2): 101-127. （责任编辑：齐 霁）
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料