论文研究- 基于2D-LDA的低分辨率人脸识别 .pdf-资料库

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 基于 2D-LDA 的低分辨率人脸识别 # 赵迪，陈振学，李翠萍** （山东大学控制科学与工程学院，济南 250061）摘要：在处理视频监控中的人脸识别时，低分辨是一个具有挑战性的问题。为了解决这个问题，本文提出了一种基于二维线性判别分析（Two-dimensional Linear Discriminant Analysis, 2D-LDA）和度量学习的方法来匹配低分辨和高分辨人脸图像。2D-LDA 将低分辨和高分辨图像转换到一个共同的空间，在这个空间中保留了它们之间最有鉴别性的信息。而且它是基于矩阵的运算，因此克服了矩阵奇异和空间信息丢失的问题。为了进一步提高识别性能，本文采用了基于近邻成分分析（Neighbourhood Component Analysis, NCA）的度量学习方法，它的目标是最大化留一法（Leave-one-out, LOO）分类准确率。在 ORL 人脸库上的实验证明这个方法能够有效地提高识别率。关键词：低分辨；二维线性判别分析；鉴别性的信息；距离度量；近邻成分分析中图分类号：TP391.4 Two-dimensional Linear Discriminant Analysis for Low-Resolution Face Recognition ZHAO Di, CHEN Zhenxue, LI Cuiping (School of Control Science and Engineering, Shandong University, Jinan 250061) Abstract: Low resolution (LR) is a challenging problem when handling video surveillance face recognition. To address this problem, this paper proposes an approach for matching low resolution images with high resolution (HR) images based on Two-dimensional Linear Discriminant Analysis (2D-LDA) and metric learning method. The 2D-LDA method transforms the LR and HR images into a common space such that the most discriminative information between them is preserved. Also, it overcomes the singularity and loss of the spatial information problem because of its matrix representation. To further improve the recognition performance, metric learning method is used based on Neighbourhood Component Analysis (NCA) which aims to maximize the Leave-one-out (LOO) classification accuracy. Experiments on the ORL database illustrate that this method can improve the recognition accuracy effectively. Key words: Low Resolution; 2D-LDA; Discriminative Information; Metric Learning; NCA 0 引言近年来，在约束条件下的人脸识别取得了很大的成功。然而，随着监控摄像头的广泛应用，在非约束环境下，低分辨率的问题日益显著，从而导致了鉴别性信息的丢失。因此，低分辨率人脸识别问题仍然是一个极具挑战性的问题。现有的低分辨率人脸识别方法可以被分为三类[1]。一类是人脸幻想[2]，它通过从低分辨人脸图像中重建高分辨人脸图像来实现。人脸幻想中的大部分方法更多地关注重建图像的视觉效果而非识别率，而且，它的计算复杂度比较高。第二种方法是提取分辨率稳健特征[3-4]。这种方法的缺点是没有考虑高低分辨率图像对之间的关系。最近，一系列基于映射[5]的工作得到了广泛关注，这些方法的思路是将高分辨率和低分基金项目：国家自然科学基金项目(61203261)；江苏省大数据分析技术重点实验室(南京信息工程大学) 开放课题(KXK1404)；广西多源信息挖掘与安全重点实验室开放基金（MIMS16-02）作者简介：赵迪（1993-），女，硕士研究生，主要研究方向：模式识别与图像处理、低分辨率人脸识别等通信联系人：陈振学（1977-），副教授、硕导，目前研究方向：生物特征识别与机器视觉、人脸识别与信息融合等. E-mail: chenzhenxue@sdu.edu.cn - 1 -

http://www.paper.edu.cn 中国科技论文在线辨率图像以一个特定的目标映射到一个共同的空间。Li 等人[6]学习了一对耦合映射，其将不同分辨率的图片映射到一个统一的特征空间。此外，在目标函数中引入了一个惩罚权值矩阵来保持局部的关系。Ren 等人[7]提出了一种耦合核嵌入的方法，其目标是保持核希尔伯特空间中近邻之间的位置并且最小化低分辨和高分辨空间的不相似程度。Zhou 等人[8]引入了一种同时鉴别分析方法。通过两个映射将高低分辨图像对映射到了一个具有鉴别性的空间中。 Biswas 等人[9]用了多维尺度分析方法。其思路为同时将低分辨测试图像和高分辨率参考图像嵌入到一个共同的空间，使得在转换空间中它们之间的距离接近两者均为高分辨率图像时的距离。本文提出了一种基于 2D-LDA 的新的低分辨率人脸识别算法，其主要思路是通过 2D-LDA 学习了一个映射，将低分辨率和高分辨率两种模态的图片转换到一个共同的空间。基于 NCA 的度量学习方法更进一步地提高了识别性能。本文最主要的贡献简述如下： (1) 在训练阶段，学习了一个基于 2D-LDA 的带有鉴别性信息的转换矩阵。通过这个转换矩阵，HR 和 LR 图像之间的类间和类内信息得以探索。此外，由于 2D-LDA 直接对图像进行处理，即基于矩阵表达，因此使得图像的空间信息保存了下来。 (2) 提出了一种基于 NCA 的距离度量学习方法。这个方法的目标是通过在转换空间最大化留一法正确率，寻找一个应用于低分辨率人脸识别的最优距离度量。本文提出的方法不仅考虑了高低分辨率图像对之间的关系，而且引入了鉴别性信息，这对低分辨人脸识别非常重要。 1 基于 2D-LDA 的转换矩阵的学习线性判别分析（Linear Discriminant Analysis, LDA）将数据映射到一个空间，以致类间散度与类内散度的比值最大化。因此，它获得了数据之间最具鉴别性的信息，这一信息是提高低分辨率人脸识别性能的关键。然而，LDA 中的类内散度矩阵在实际应用中可能会奇异，而且 LDA 是将图像像素点排列成向量进行运算的，因此会损失图像的空间信息。为了克服 LDA 算法的限制，本文采用 2D-LDA[10]的方法。这一方法用训练集中的高分辨率和低分辨率图像学习了一个有鉴别性的转换矩阵。特别地，原始图像直接采用二维矩阵的形式而不是一维向量，这是 2D-LDA 和 LDA 之间最主要的不同。因此，对识别有利的人脸空间结构信息更好地保存了下来。具体实现过程如下。给定一个包含 M 幅 HR-LR 人脸图像对的训练数据集，每一幅图像通过一个原始的像素矩阵表达。假定有 c 个类别， iM 是第i 个类别中训练样本的数量。反映 HR-LR 图像对之间关系的类内类间散度矩阵可以用如下公式表示。 45 50 55 60 65 70 H L S w  L H S w  75 H L S b  1 M 1 M 1 M c iM   i  1 j 1  iM c   i  1 j  1 ( H ij  L i )  ( H  L i ) ij (1) ( L ij  H  ) i ( L ij  H ) i (2) c  i  1 M H ( i  i  L ) ( H  i L ) (3) - 2 -

80 85 (5) 中国科技论文在线 http://www.paper.edu.cn L H S b  1 M c  i  1 M L ( i  H  ) ( L i i  H ) (4) 其中 H 和 L 分别表示所有 HR 和所有 LR 训练样本的均值图像， iH 是第i 类中 HR 训练图像的均值矩阵，同样 iL 是指第i 类中 LR 训练图像的均值矩阵。 ijH 和 ijL 分别表示第i 类中的第 j 张 HR 和 LR 图像。 HL wS 代表 HR 和 LR 的类内散度矩阵，它是通过构建同一类中每 wS 有一张 HR 图像和该类所有 LR 图像的均值图像的差异获得的。 LH 相同的定义方法。基于上述公式，对应 HR 和 LR 的类之间的关系可以最终写为： bS 与 HL wS bS LH HL , , w S S b   S S b HL w HL S  S  b LH w LH 若W 表示转换矩阵。2D-LDA 的目标就是学习一个有鉴别性的转换矩阵W ，它可以最 (6) 大化类间距离并且最小化类内距离。从这个角度出发，本文引入以下判别准则[11-12] 90 J W ( )   W S W W S W  b w (7) W 当准则(7)最大时，获得最优转换矩阵 * S w 问题的求解等价于如下广义特征值问题： b 个最大特征值所对应的特征向量。 95 2 基于 NCA 的度量学习 , , , w ]d w w [   。为了获得 *W ，这个优化 2 1 S w 的前 d 。因此， *W 是对应 S 1 b S w w 基于以上分析，HR 训练样本和 LR 测试样本首先通过训练阶段学习到的转换矩阵 *W 映 testL 表示在共同的空间中对应 HR 训练图像和 LR 测试图像的特征矩射到新的空间。若 ˆH 和 ˆ 阵，则： ˆ L test L W test * (8) testL 矩阵转化为一个 L 维的向量 ˆh 和 ˆ l ，其中向量是通 test 100 105 * ˆH HW 为了后续的处理，本文将 ˆH 和 ˆ 过依次连接每一列的像素获得的。 ˆ h y , ), i i  1, 2,  (  iy ˆ h y 1 1 ˆ h y 2 ), ( {( D 让 ),  , , 2  ˆ h , ( M  c , y M )} 表示 HR 映射后的训练样本集， ˆ ih 作为一个 L 维的特征向量，其中  。为了进一步提高分类器的性能，本文采用 NCA 的方法引入了一个合适的距离度量[13-14]，其目的是学习一个特征权向量来更好地选择对分类有更大贡献的特征。对进行学习要设置一个目标，本文将直接嵌入到近邻分类 - 3 -

中国科技论文在线器的评价指标中去，希望提高近邻分类器的性能。这一步骤的优化仅采用 HR 训练样本。任意两个 HR 训练样本 ˆ jh 之间的权值距离定义为 http://www.paper.edu.cn ih 和 ˆ 110 其中 l 表示第 l 个特征权值。 ˆ D h h ( , ˆ i )  j L  l 1  2  l ˆ h il ˆ h  jl (9) 假定留一法分类准确率是最近邻分类器性能的评价指标。本文的目标是在训练样本集 115 D 上最大化留一法准确率。因此，对于任意样本 ˆ jh ，它对 ˆ ih 分类结果影响的概率为： p ij       exp(  exp( ˆ ˆ D h h , )) ( i ˆ ˆ D h h (  i j ,  0, k i  , )) j if i  if i  j j (10) 显然， ˆ jh 对 ˆ ih 的影响随着它们之间距离的增大而减小。HR 训练样本 ˆ ih 的留一法正确 120 率，即它被自身之外的所有样本正确分类的概率为： p i   (11) p ij j  i 其中， i 表示和 ˆ ih 同一个类别的样本集。然后整个样本集上的留一法正确率可写为： 125 F ( )     (12) p ij M i 1   j i 此外，为了防止过拟合，在公式(12)中引入正则项，从而获得以下目标函数： 130 f ( )    ( M   i 1  j  p ij  i  (13) 2   l ) L l  1 135 其中正则化参数可以通过五折交叉验证进行调整，寻找权值向量可以进一步表示为如下最小化问题：为了求解特征权重，采用随机梯度下降算法最小化(14)中的目标函数。然后，本文利用特征权值 和一个相对的阈值  来选择对分类更重要的特征。其中，特征权值满足 i  (14) 。最终可以求得最优特征权值 * 。 m ax(1, m ax( arg min ( )  *   ))    f - 4 -

140 145 150 155 160 165 170 中国科技论文在线 3 分类 http://www.paper.edu.cn 基于 * ，HR 训练图像和 LR 测试图像最终的特征向量可以表示为： h  进行选择后的特征采用欧氏距离进行度量。  * ˆ h  l   ˆ l te s t *  (15) d  l    h i i  1 2 l  i (16) 其中， l  表示特征向量的长度。两幅图像之间的欧式距离越小，表明图像越相似。最后，本文采用了最近邻分类器进行分类识别，即根据距离最近的训练样本的类别对测试样本进行归类。 4 实验结果与分析本文在 ORL 人脸库上进行了实验，从而来评估本文提出的算法在低分辨率人脸识别中的性能。 4.1 特定分辨率下的算法分析 ORL 人脸库总共包含 40 个人的 400 张人脸图像，其中有光照、姿态和表情变化。在下面的实验中，HR 训练图像的分辨率保持在原始分辨率，即 112 92。特别地，特定低分辨图像是通过双三次插值算法进行下采样获得的。为了进行后续地识别，用同样的方法进行上采样到 112 92，即上采样之后的图像作为对应分辨率下的图像。以分辨率为12 10 (下采样 10 倍)像素的低分辨率样本为例进行实验和分析。图 1 展示了 ORL 人脸库中部分图像示例。 (a) (b) (c) 图 1 (a)分辨率为112 92 的 HR 图像；(b)分辨率为12 10 的 LR 图像；(c) 双三次插值后的图像本文选择了每个人 HR 和 LR 图像各 6 幅作为训练样本，剩下的 LR 图像作为测试样本。首先衡量在改变最优转换矩阵的维度 d 和正则化参数时的性能。本文先固定最优转换矩 - 5 -

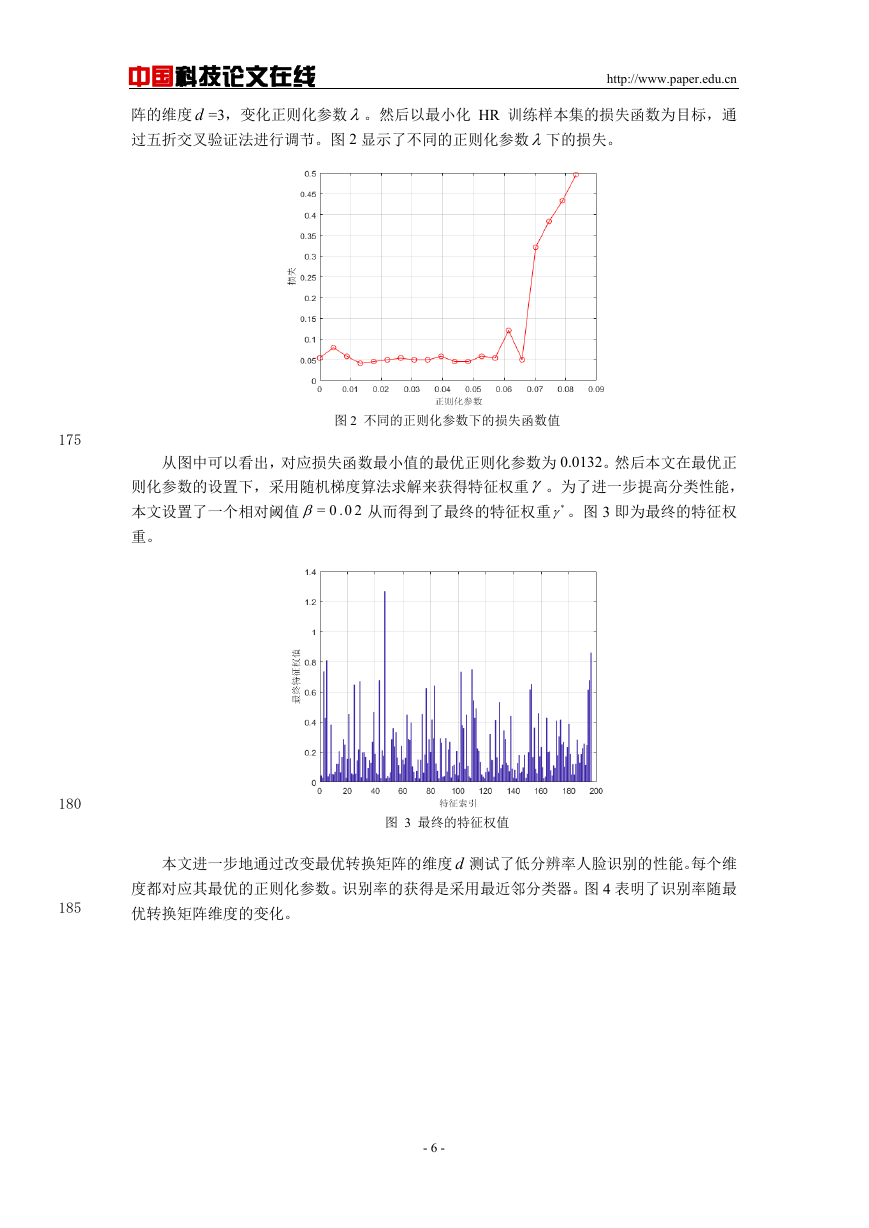
中国科技论文在线阵的维度 d =3，变化正则化参数。然后以最小化 HR 训练样本集的损失函数为目标，通过五折交叉验证法进行调节。图 2 显示了不同的正则化参数下的损失。 http://www.paper.edu.cn 175 180 185 图 2 不同的正则化参数下的损失函数值从图中可以看出，对应损失函数最小值的最优正则化参数为 0.0132。然后本文在最优正则化参数的设置下，采用随机梯度算法求解来获得特征权重。为了进一步提高分类性能，本文设置了一个相对阈值 = 0 .0 2 从而得到了最终的特征权重 * 。图 3 即为最终的特征权重。  图 3 最终的特征权值本文进一步地通过改变最优转换矩阵的维度 d 测试了低分辨率人脸识别的性能。每个维度都对应其最优的正则化参数。识别率的获得是采用最近邻分类器。图 4 表明了识别率随最优转换矩阵维度的变化。 - 6 -

中国科技论文在线 http://www.paper.edu.cn 图 4 不同维度下的最优转换矩阵对应的识别率如图 4 所示，识别率随矩阵维度的不同而变化，但两者之间并没有明显的关系。为了后续比较，本文选择对应最好识别率下的矩阵维度。因此，在分辨率为12 10 时，识别率达到 91.88%. 4.2 不同分辨率下的性能比较在这一节，本文通过在 ORL 人脸库上下采样到不同的分辨率进行实验。为了证明本文提出算法的有效性，将其与基于映射的一些方法进行了比较，其中包括二维主成分分析 (Two-dimensional Principal Component Analysis, 2D-PCA), 核化主成分分析(Kernel Principal Component Analysis, KPCA), 线性鉴别分析(Linear Discriminant Analysis, LDA), 边际费舍尔分析(Marginal Fisher Analysis，MFA)。在 ORL 人脸库上下采样到五个分辨率，分别为 56 46 , , 14 12 和12 10 ，分别对应原始分辨率的 2,4,6,8,10 倍。特别地，五种分 28 23 辨率下的识别率的实验步骤与 4.1 中是相同的。此外，为了避免矩阵奇异，在 LDA 和 MFA 算法之前都加入了 PCA 降维操作。 , 19 16 190 195 200 图 5 ORL 人脸库上的识别率比较 - 7 -

中国科技论文在线 http://www.paper.edu.cn 从图 5 可以看出，本文提出的算法在分辨率变化的情况下实现了相对较高的识别率，有 205 效提高了 ORL 人脸库上低分辨人脸识别的性能。 5 结论本文提出了一种新的方法来解决低分辨率人脸识别的问题。其主要思想是基于 2D-LDA 算法学习一个带有鉴别性的转换矩阵。通过这个转换矩阵，HR 和 LR 图像之间的关系以及最有鉴别性的信息得以保留。为了进一步提高识别的性能，本文引入了一种基于 NCA 的距离度量方法，通过这个方法获得了特征权值进而选择了对识别更有效的特征。在 ORL 人脸库上的实验表明了本文提出算法的有效性。在未来的工作中，会将该方法进行改进从而更好地应用于监控视频中。 [参考文献] (References) [1] Wang Z, Miao Z, Wu Q M J, et al. Low-resolution face recognition: a review[J]. The Visual Computer, 2014, 30(4):359-386. [2] Wang N, Tao D, Gao X, et al. A Comprehensive Survey to Face Hallucination[J]. International Journal of Computer Vision, 2014, 106(1):9-30. [3] Lei Z, Ahonen T, Pietikäinen M, et al. Local frequency descriptor for low-resolution face recognition[C]// IEEE International Conference on Automatic Face & Gesture Recognition and Workshops. IEEE, 2011:161-166. [4] Li J, Chen Z, Liu C. Low-Resolution Face Recognition of Multi-Scale Blocking CS-LBP and Weighted PCA[J]. International Journal of Pattern Recognition & Artificial Intelligence, 2016, 30(8). [5] Ouyang S, Hospedales T, Song Y Z, et al. A Survey on Heterogeneous Face Recognition: Sketch, Infra-red, 3D and Low-resolution [J]. Image & Vision Computing, 2016, 56:28-48. [6] Li B, Chang H, Shan S, et al. Low-Resolution Face Recognition via Coupled Locality Preserving Mappings[J]. Signal Processing Letters IEEE, 2010, 17(1):20-23. [7] Ren C X, Dai D Q, Yan H. Coupled Kernel Embedding for Low-Resolution Face Image Recognition[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2012, 21(8):3770-83. [8] Zhou C, Zhang Z, Yi D, et al. Low-resolution face recognition via Simultaneous Discriminant Analysis[C]// International Joint Conference on Biometrics. IEEE, 2011:1-6. [9] Biswas S, Bowyer K W, Flynn P J. Multidimensional scaling for matching low-resolution face images[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 34(10):2019-2030. [10] Li M, Yuan B. 2D-LDA: A statistical linear discriminant analysis for image matrix[J]. Pattern Recognition Letters, 2005, 26(5):527-532. [11] Ye J, Janardan R, Li Q. Two-Dimensional Linear Discriminant Analysis[J]. Photogrammetric Engineering & Remote Sensing, 2005, 5(6):págs. 1431-1441. [12] Yang J, Zhang D, Yong X, et al. Two-dimensional discriminant transform for face recognition[J]. Pattern Recognition, 2005, 38(7):1125-1129. [13] Butman M, Goldberger J. Face Recognition Using Classification-Based Linear Projections[J]. EURASIP Journal on Advances in Signal Processing, 2007, 2008(1):1-7. [14] Yang W, Wang K, Zuo W. Neighborhood Component Feature Selection for High-Dimensional Data[J]. Journal of Computers, 2012, 7(1):161-168. 210 215 220 225 230 235 240 - 8 -

资料库

论文研究- 基于2D-LDA的低分辨率人脸识别 .pdf

相关推荐

开发技术

热门标签

最新资料