第1页 / 共35页
第2页 / 共35页
第3页 / 共35页
第4页 / 共35页
第5页 / 共35页
第6页 / 共35页
第7页 / 共35页
第8页 / 共35页
Matlab辅助激光光学分析与应用.pdf
Matlab辅助激光光学分析与应用
第一章 光的波动性和衍射
1.1 Maxwell方程组和电磁波
1.2 波动方程
1.3 衍射
1.3.1 小孔衍射
1.3.2 双缝衍射
1.4 波前畸变
1.4.1 Zernike多项式
1.4.2 畸变光束的衍射
1.5 光束通过光学元件的变换
1.5.1 平行光束通过透镜的聚焦
1.5.2 高斯光束通过透镜的聚焦
1.5.3 自聚焦透镜
1.6 高斯光束
1.6.1 高阶高斯光束
1.6.2 高斯光束的传输变换
第二章 激光谐振腔
2.1 激光谐振腔的本征方程
Matlab辅助激光光学分析与应用
作 者：刘良清 Email：llq-hust@sohu.com
单 位：武汉凌云光电科技有限公司
毕业院校：华中科技大学激光技术与工程学院
学 历：硕士研究生
研究方向：自适应光学、非线性光学、激光光学、固体激光
器件
2008 年 3 月 第一版
第一章 光的波动性和衍射
1.1 Maxwell方程组和电磁波
十八世纪中叶，James Maxwell 将已知的各种电磁作用关系用一组方程组合起来，形
成了一个方程组：
ρ
ε
∇ =·E
0∇ =·B
E
∇× +
B
μ
∇×
0
(源于库伦定律的高斯定律)
0
(源于毕奥-萨瓦尔定律的高斯定律)
B
∂
∂
t
− ε
(法拉第定律)
(Maxwell 修正的安培定律)
=
J
0
0
=
E
∂
∂
t
(1.1)
(1.2)
(1.3)
(1.4)
2
2
·
/C N m
12
−
式中， 和 分别代表了电场和磁场分量。电荷密度
分布；电流 描述电荷的移动( 单位电荷乘以速度) 。
ε =
0
k
者
E B
J
8.854 10
×
g m C·
2
在安培定律中引入了一个关键参数之后，Maxwell 意识到，方程组构成了一个完美的电
磁现象自洽理论。此外，方程组预言了电磁波的存在，并以光速传播。在 Maxwell 时代之
前就已经有人对光速进行了测量，因此一个显而易见的结果(当时还难以令人置信)便是，光
是一种高频振荡表现，类似并超越了支配电流和电荷的影响因素。而在此之前，光学还仍然
ρ 描述路径空间单位体积内的电荷量
0ε 表示真空介电常数，其值为
（或
0μ
。 表示真空磁导率常数，其值为
/T m A
7
−
μ = π×
0
）。
10
4
/
·
作为一种独立于电学和磁学的主体进行讨论的。
这里，我们不再对电磁学的基本知识进行详细的讨论，因为它们在普通物理课程中都有
讲述，并且有大量的文献和书籍对其进行了细致的分析。但我们要简要的从波动方程出发，
求解旁轴近似下的 Maxwell 方程组，得到激光传输与变换的基本方程，以方便我们后续的
讨论和应用。
为了体现 Matlab 在可视化方面的优势，我们先以一个简单的例子作为本书的开篇，以
达到抛砖引玉的效果。在电动力学中，我们会遇到真空电磁场波动方程的旁轴近似解，众所
周知，其解为具有高斯分布的电场复振幅：
Ψ
( ,
r z
)
= Ψ
0
2
π
w
0
( )
w z
= π λ
2 /
k
式中，
表示为：
为光波传播常数。
exp
j
−
⎡
⎢
⎣
( )w z
2
−
r
2
2
kr
2 ( )
( )
R z w z
( )R z
、
}
] (1.5)
( )φ z 是与光束有关的传播参数。分别
[
j kz
exp
( )
z
− φ
⎤
⎥
⎦
{
、
−
( )
w z w
=
1
⎛
λ
z
+ ⎜ π⎝
w
2
0
2
⎞
⎟
⎠
0
(1.6)
1
光束远场发散角为：
或者
( )
R z
=
z
⎡
1
⎢
⎢
⎣
( )
φ
z
=
tan
− ⎛
1
⎜
⎝
z
Z
⎛
+ ⎜
⎝
⎞
⎟
⎠
R
0
2
π
w
λ
z
2
⎞
⎟
⎠
,
Z
R
=
⎤
⎥
⎥
⎦
π
2
0
w
λ
θ =
0
lim
→∞
z
( )
w z
z
=
λ
π
w
0
θ =
0
( )
w z
( )
R z
⎛
⎜
⎝
2
⎞
⎟
⎠
+
⎛
⎜ π
⎝
λ
( )
w z
⎞
⎟
⎠
2
(1.7)
(1.8)
(1.9)
(1.10)
我们可以用几行简单 matlab 程序就可以画出具有高斯分布的电场强度，如图 1.1 所示，图
形美观，方便对光强的分布有一个感性的视觉认识。程序代码为：
clear;
clc;
w0=0.5;
r=linspace(0,3*w0,200);
eta=linspace(0,2*pi,200);
[rho,theta]=meshgrid(r,eta);
[x,y]=pol2cart(theta,rho);
Iopt=exp(-2*rho.ˆ2/w0ˆ2);
surf(x,y,Iopt);
shading interp;
xlabel(’位置 /mm’);
ylabel(’位置 /mm’);
zlabel(’相对强度 /a.u.’);
title(’高斯强度分布’);
axis([-3*w0,3*w0,-3*w0,3*w0,0,1]);
colorbar;
colormap(’hot’);
box on;
grid off;
图 1.1 高斯光强分布
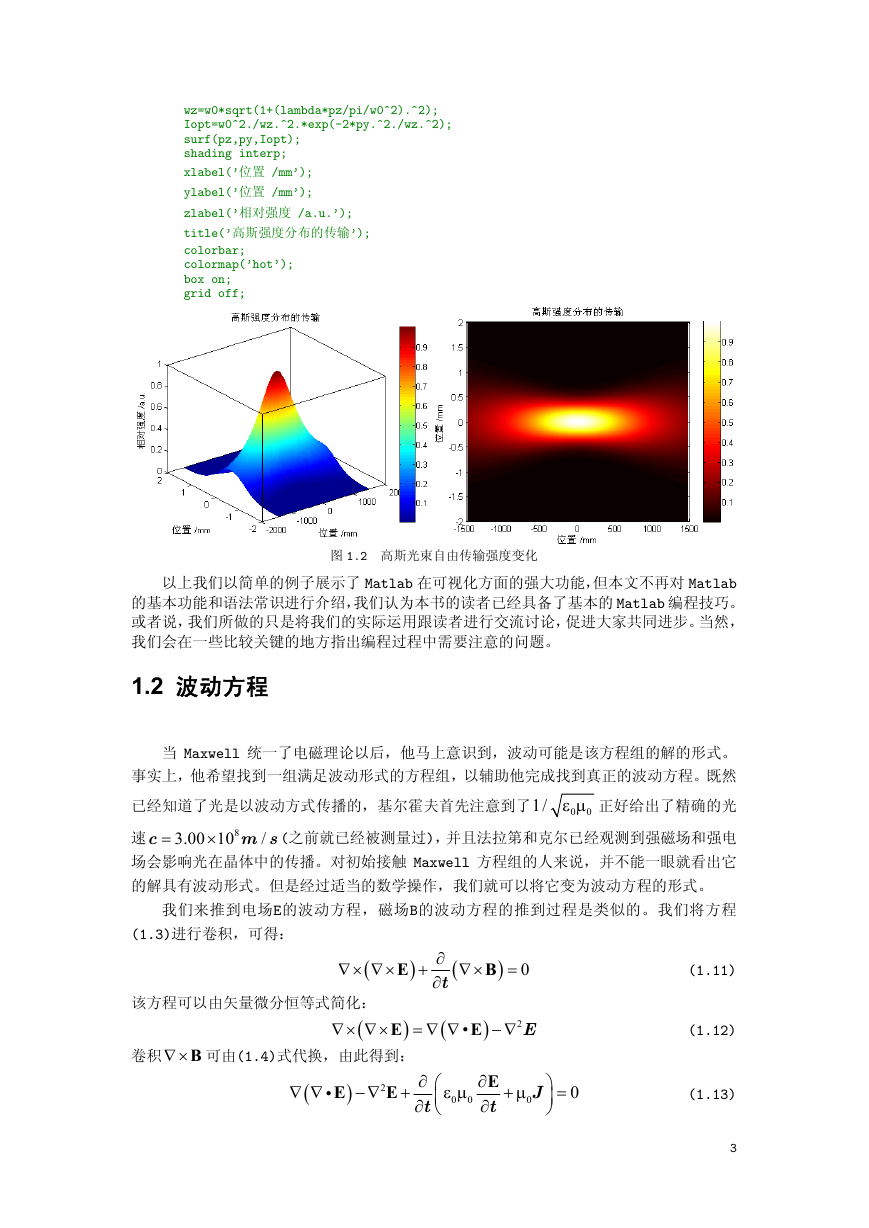
另外，我们还可以画出高斯光束在自由传输过程中的强度变化，如图 1.2 所示，程序代码
如下：
clear;
clc;
lambda=1.064e-3;
w0=0.5;
ZR=pi*w0ˆ2/lambda;
z=linspace(-2*ZR,2*ZR,200);
y=linspace(-4*w0,4*w0,200);
[py,pz]=meshgrid(y,z);
2
wz=w0*sqrt(1+(lambda*pz/pi/w0ˆ2).ˆ2);
Iopt=w0ˆ2./wz.ˆ2.*exp(-2*py.ˆ2./wz.ˆ2);
surf(pz,py,Iopt);
shading interp;
xlabel(’位置 /mm’);
ylabel(’位置 /mm’);
zlabel(’相对强度 /a.u.’);
title(’高斯强度分布的传输’);
colorbar;
colormap(’hot’);
box on;
grid off;
图 1.2 高斯光束自由传输强度变化
以上我们以简单的例子展示了 Matlab 在可视化方面的强大功能，但本文不再对 Matlab
的基本功能和语法常识进行介绍，我们认为本书的读者已经具备了基本的 Matlab 编程技巧。
或者说，我们所做的只是将我们的实际运用跟读者进行交流讨论，促进大家共同进步。当然，
我们会在一些比较关键的地方指出编程过程中需要注意的问题。
1.2 波动方程
当 Maxwell 统一了电磁理论以后，他马上意识到，波动可能是该方程组的解的形式。
事实上，他希望找到一组满足波动形式的方程组，以辅助他完成找到真正的波动方程。既然
1/ ε μ 正好给出了精确的光
已经知道了光是以波动方式传播的，基尔霍夫首先注意到了
0
0
c =
3.00 10
/
× m s
8
速
(之前就已经被测量过)，并且法拉第和克尔已经观测到强磁场和强电
场会影响光在晶体中的传播。对初始接触 Maxwell 方程组的人来说，并不能一眼就看出它
的解具有波动形式。但是经过适当的数学操作，我们就可以将它变为波动方程的形式。
我们来推到电场E的波动方程，磁场B的波动方程的推到过程是类似的。我们将方程
(1.3)进行卷积，可得：
∇ × ∇ ×
(
E
)
+
∂
∂
t
(
∇ ×
B
) 0
=
该方程可以由矢量微分恒等式简化：
∇× ∇×
∇ ×B
卷积
可由
(1.11)
(1.12)
(1.13)
3
(
= ∇ ∇
•
E
)
2
− ∇
E
(
E
)
(1.4)式代换，由此得到：
∂
⎛
⎜∂
⎝
t
− ∇ +
(
∇ ∇
E
E
)
•
2
ε μ
0
0
E
∂
∂
t
+ μ
J
0
⎞
0⎟
=
⎠
再由(1.1)式代入上式，经过整理就可得到：
2
∇ − ε μ
0
E
0
∂
∂
2
E
2
t
= ∇
⎛
⎜
⎝
ρ
ε
0
⎞
⎟
⎠
+ μ
0
∂
J
∂
t
(1.14)
需要指出的是，上式中没有考虑到介质的极化。弱考虑到介质的极化和实际一般光学问题中
自由电荷为零的条件，上式修正为：
2
∇ − ε μ
0
E
2
E
∂
2
∂
t
0
= μ
0
∂
freeJ
∂
t
+ μ
0
2
∂
P
2
∂
t
(
− ∇ ∇
1
ε
0
•
P
)
(1.15)
式中， P 为极化强度矢量。这样我们得到了一般的电场传播方程，该方程在非线性光学中
有很重要的地位。当光在真空中传播时，式(1.15)中的右边所有项均为零，方程简化为：
2
∇ − ε μ
0
E
2
E
∂
2
∂
t
0
=
0
(1.16)
这样我们就得到了电场传播的波动方程形式。当然在有些实际问题中，式(1.15)中右边的
项并不是都为零，至少会有一项不为零，这与介质的性质有关。
1.3 衍射
考虑一个振动频率为 的光场，其复振幅可以表述为
ω
E
(
)
r e− ω
j
t
，则它也必须满足波
动方程：
∇
2
E
(
)
r e
− ω
j
t n
−
c
2
2
E
(
r
)
2
∂
− ω
t
j
e
∂
t
2
0
=
(1.17)
由于电场振幅的含时部分是显式给出的，则方程(1.17)可以简化为：
式中
k n
≡ ω
∇
(1.18)式就是所谓的赫姆霍兹方程。如果我们忽略波动
是波矢量的大小。
的矢量特性，而只考虑它的振幅(这里不再详细讨论其过程)，那么在标量近似下，就得到了
标量赫姆霍兹方程：
−
k
c
r
r
/
(1.18)
0
=
2
E
(
)
2
E
(
)
2
∇
(
E r
)
−
2
(
k E r
)
0
=
然后，我们考虑一束沿z轴传播的光束，它的电场复振幅写成 (
)
E x y z e
将它代入标量赫姆霍兹方程(1.19)式，得到：
∂
E
∂
z
∂
E
2
∂
z
jk
j kz
+
+
=
2
0
e
,
,
2
2
⎞
⎟
⎠
(1.19)
j kz
的形式。我们
(1.20)
2
⎛
∂
E
⎜ ∂
2
x
⎝
∂
2 E
k
∂
z
+
∂
E
2
∂
y
∂
E
2
∂
z
2
在旁轴近似下，有
。即是说，我们假设了电场的复振幅沿 z 轴传播方向是
缓慢变化的，与平面波类似。但是我们允许振幅沿 z 轴在远大于波长量级的范围上有明显的
变化。这样就得到了旁轴波方程：
2
2
(1.21)
⎛
∂
⎜ ∂
⎝
x
+
2
∂
∂
y
2
+
2jk
∂
∂
z
⎞
⎟
E
⎠
≅
0
求解方程(1.21)式，得到：
)
,
E x y z
(
,
≅ −
j
z
λ ∫∫
Σ
,
′
E x y
(
,0
′
)
e
j
k
2
z
(
⎡
⎢
⎣
−
x x
2
′
)
(
+ −
y y
′
)
2
⎤
⎥
⎦
dx dy
′
′
(1.22)
4
于是电场的表达式为：
,
,
)
E x y z E x y z e
=
(
)
(
,
,
j kz
≅ −
j
z
λ ∫∫
Σ
,
′
E x y
(
,0
′
)
e
(
−
x x
′
)
2
′
)
2
(
+ −
y y
2
z
j k
⎡
⎢
⎢
⎣
⎤
⎥+
z
⎥
⎦
dx dy
′
′
(1.23)
值得一提的是，基尔霍夫早在 1887 年就提出了著名的菲涅耳-基尔霍夫衍射
公式：
,
E x y z
,
(
)
= −
式(1.23)和(1.24)在分母
r
j kr
e
(
,0
′
,
′
E x y
∫∫
2
aperture
时具有一致性，并在指数上：
r
)
r z
1 cos( , )
+⎡
⎢
⎣
j
λ
z≅
dx dy
′
′
(1.24)
⎤
⎥
⎦
(
−
x x
′
)
r
≅ +
z
同时，式(1.23)是(1.24)式在满足
外，如果进一步满足远场条件
(
k x
′
2
(
+
2z
)
2
+
−
y y
2
′
)
(1.25)
(
−
y y
2
′
)
条件下的菲尼尔旁轴近似。另
′
，就得到夫琅禾费衍射近似：
z
−
x x
)
2
z
2
(
′+
y
2
⎛
⎜
⎜
⎝
2
+
y
2
z
x
j k
,
E x y z
,
(
)
≅ −
j
λ
z
e
2
+
z
⎞
⎟
⎟
⎠
∫∫
Σ
,
′
E x y
(
,0
′
)
e
j k
xx yy
′
+
z
′
dx dy
′
′
(1.26)
1.3.1 小孔衍射
假设光场透过一个圆柱
对称的小孔，这时，孔径上的场分布可以写为：
,
′
E x y
(
,0
′
)
=
E
(
,0
′
ρ
)
(1.27)
这样
，二维衍射积分可以简化为一维衍射积分。将(1.27)式代入到菲尼尔衍射
积分公式中，
得到简化衍射积分式：
,
ρ
E z
(
)
≅
−
j
λ
z
e
j k
2
ρ
2
z
⎛
⎜
⎜
⎝
+
z
⎞
⎟
⎟
⎠
∫
Σ
′
′
ρ ρ
d E
(
,
′
ρ
0
)
e
j k
对角度的积分项，我们可以借助下面的公式完成：
2 2
ρ
2
z
π
∫
0
−
j k
′
ρρ
z
cos
(
′
θ−θ
)
′
θ
d e
(1.28)
2
π
∫
0
−
j k
′
ρρ
z
cos
(
′
θ−θ
)
′θ
d e
2
= π
J
0
′ρρ
k
z
⎛
⎜
⎝
⎞
⎟
⎠
式中， 称为零阶Bessel函数。这样，(1.28)式可以简化为：
0J
,
ρ
E z
(
)
≅ −
j k
2
ρ
2
z
⎛
⎜
⎜
⎝
+
z
⎞
⎟
⎟
⎠
2
π
j
λ
z
e
∫
Σ
′
′
ρ ρ
d E
(
,0
′
ρ
)
e
j k
2
ρ
2
z
J
0
⎛
⎜
⎝
k
′
ρρ
z
⎞
⎟
⎠
(1.29)
(1.30)
式(1.30)中的积分项也称为
,0
等于 1，积分项变为
E ′ρ
(
E
)
2
ρ
2
z
j k
)
′ρ
,0
ρ
的汉克尔变换。在夫琅禾费衍射近似下， 2j k
z
(
的汉克尔变换。于是夫琅禾费柱对称圆孔衍射方程为：
e
e
2
项
(
,
ρ
z
)
≅
−
E
j k
2
⎛ ρ
⎜
⎜
2
z
⎝
+
z
⎞
⎟
⎟
⎠
2
π
j
λ
z
e
∫
R
′
′
ρ ρ
d E
(
,
′
ρ
0
)
J
0
⎛
⎜
⎝
k
′
ρρ
z
⎞
⎟
⎠
(1.
31)
5
虽然经过了一系列简化，然而
E ′ρ
,0
(
)
是复振幅通常都是不确定的，即使知道了强度
分布，相位分布也可能是比较难预测的。
当然，
布。
这里，我们以平面波入射为例，
讨论圆
也可以通过辅助手段测量强度分布和相位分
E ′ρ 可用常数
孔夫琅禾费衍射问题。这时 (
,0
)
代替，不妨设为 1。利用 Bessel 函数的递推关系，我们可以得到解析的圆孔夫琅禾费衍射
公式：
()
,
ρ
z
E
≅ −
j k
2
ρ
2
z
⎛
⎜
⎜
⎝
+
z
⎞
⎟
⎟
⎠
2
π
j
λ
z
e
′
′
ρ ρ
d J
0
∫
R
′
ρρ
k
z
⎛
⎜
⎝
⎞
⎟
⎠
= −
2
π
j
λ
z
e
j k
2
ρ
2
z
⎛
⎜
⎜
⎝
+
z
⎞
⎟
⎟
⎠
2
R
J
1
ρ
⎛
k R
⎜
⎝
z
/
ρ
k R z
⎞
⎟
⎠
(1.32)
即使是解析式，我们还是不能直观地感受到衍射斑的样式。下面我们利用 Matlab 给出
夫琅禾费圆孔衍射的强度分布。程序代码如下：
ce(0,2*1.22*lambda/2/R*z,201);
R=0.1;
lambda=1.064e-3;
k=2*pi/lambda;
z=1.0e3;
r=linspa
eta=linspace(0,2*pi,2
[rho,theta]=mesh
[x,y]=pol2ca
rt(theta,rho);
Bess=besselj(1,rho*R*k/z);
Ie=4*piˆ2*Rˆ2*Bess.ˆ2./(rho
surf(x,y,Ie);
axis([-max(r),max(r),-max(r)
shading interp;box on; grid
figure;plot(x(1,:),Ie(1,:),’k’,x(101,:),Ie(10
*k).ˆ2/lambdaˆ2;
grid(r,eta);
01);
,max(r),0,max(Ie(:))]);
off;
1,:),’k’);
x 10-3
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-15
-10
-5
0
5
10
15
图 1.3 夫琅禾费圆孔衍射 (孔径 0.2mm，距离 1m 远)
程序中使用了这样一个参数1.22 / Dλ ，因为平面波假设具有最小的衍射角，这个参数
就称为衍射极限角，所以在衍射区域里，只取二倍衍射极限范围就可以大致看出小孔的衍射
6
特性
。并且，对于解析表达，Mat
Bessel 函数工具箱，可以直接调用。当然，为
了能够从图上看到跟实际观测相近的衍射环，可以将相对强度分布取四次开根号，如图 1.3
下图所示。
lab 提供了
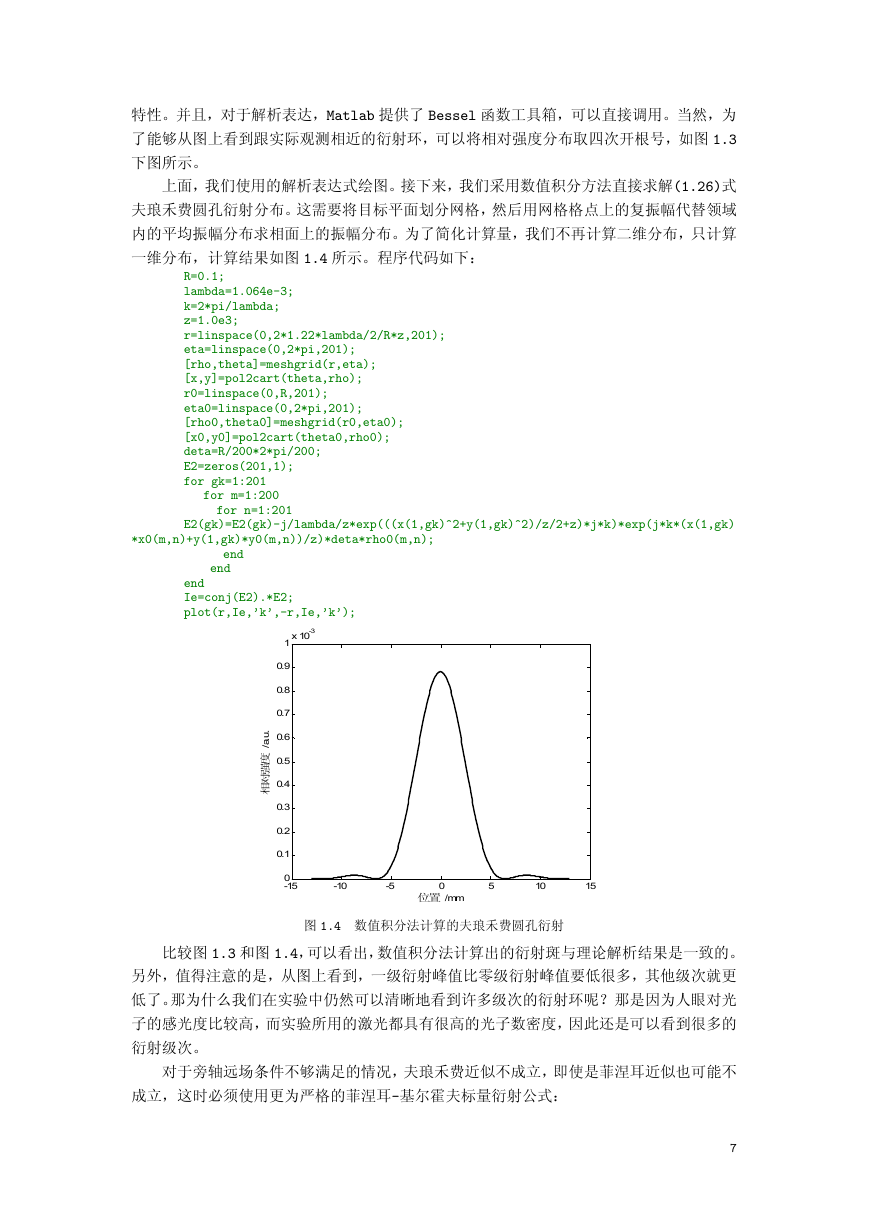
上面，我们使用的解析表达式绘图。接下来，我们采用数值积分方法直接求解(1.26)式
衍射分布。这需要将目标平面划分网格，然后用网格格点上的复振幅代替领域
夫琅禾费圆孔
内的
平均振幅分布求相面上的振幅分布。为了简化计算量，我们不再计算二维分布，只计算
一维分布，计算结果如图 1.4 所示。程序代码如下：
ambda/2/R*z,201);
meshgrid(r,eta);
*pi,201);
R=0.1;
lambda=1.064e-3;
k=2*pi/lambda;
z=1.0e3;
r=linspace(0,2*1.22*l
eta=linspace(0,2
[rho,theta]=
[x,y]=pol2cart(theta,rho);
r0=linspace(0,R,201);
eta0=linspace(0,2*pi,201);
[rho0,theta0]=meshgrid(r0,et
[x0,y0]=pol2cart(theta0
deta=R/200*2*pi/200;
E2=zeros(201,1);
for gk=1:201
for m=1:200
for n=1:201
E2(gk)=E2(gk)-
j/l
)+y(1,gk)*y0(m,n
end
end
end
Ie=conj(E2
plot(r,Ie
’,-r,Ie,’k’);
).*E2;
,’k
a0);
,rho0);
*x0(m,n
))/z)*deta*rho0(m,n);
ambda/z*exp(((x(1,gk)ˆ2+y(1,gk)ˆ2)/z/2+z)*j*k)*exp(j*k*(x(1,gk)
.
u
a
.
/
度
强
对
相
x 10-3
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-15
-10
-5
0
位置 /mm
5
10
15
图 1.4 数值积分法计算的夫琅禾费圆孔衍射
比较图 1.3 和图 1.4，可以看出，数值积分法计算出的衍射斑与理论解析结果是一致的。
低很多，其他级次就更
上看到，一级衍射峰值比零级衍射峰值要
另外，值得注意的是，从图
低了
。那为什么我们在实验中仍然可以清晰地看到许多级次的衍射环呢？那是因为人眼对光
子的感光度比较高，而实验所用的激光都具有很高的光子数密度，因此还是可以看到很多的
衍射级次。
对于旁轴远场条件不够满足的情况，夫琅禾费近似不成立，即使是菲涅耳近似也可能不
成立，这时必
须使用更为严格的菲涅耳-基尔霍夫标量衍射公式：
7
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
