2010年湖南省衡阳市中考数学真题及答案.doc

发布时间：2022-08-27 发布人：admin 分类：说明书资料大小：0.29M 资料格式：doc 举报版权申诉

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

文本预览

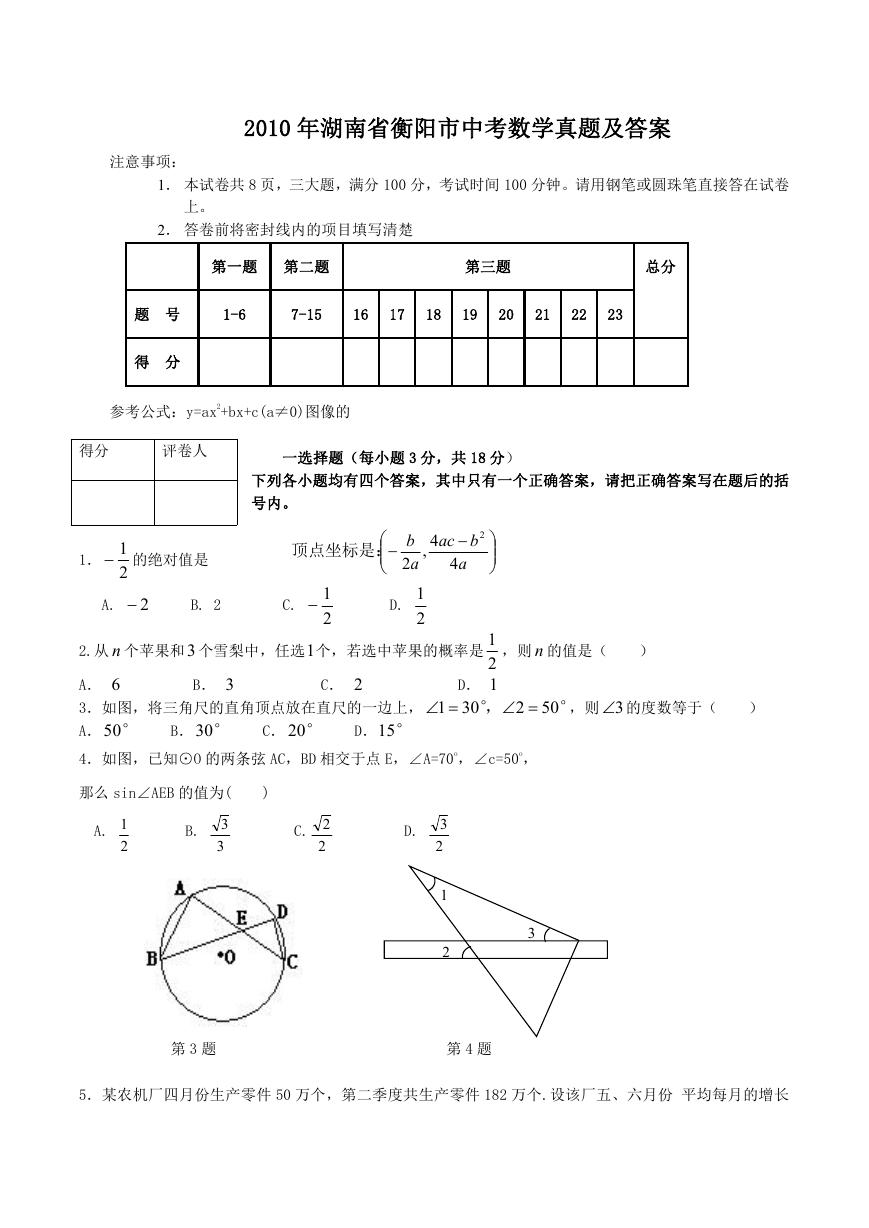
2010 年湖南省衡阳市中考数学真题及答案注意事项： 1．本试卷共 8 页，三大题，满分 100 分，考试时间 100 分钟。请用钢笔或圆珠笔直接答在试卷上。 2．答卷前将密封线内的项目填写清楚第一题第二题第三题总分题号 1-6 7-15 16 17 18 19 20 21 22 23 得分参考公式：y=ax2+bx+c(a≠0)图像的得分评卷人一选择题（每小题 3 分，共 18 分）下列各小题均有四个答案，其中只有一个正确答案，请把正确答案写在题后的括号内。 1． 1 的绝对值是 2 2 A. B. 2 C. 1 2    顶点坐标是：  4, 2 b ac  4 a    b 2 a 1 2 D. 2.从 n 个苹果和3 个雪梨中，任选1个，若选中苹果的概率是 A． 6 3．如图，将三角尺的直角顶点放在直尺的一边上， 1 30 A．50° B．30° C． 20° D．15° 4．如图，已知⊙O 的两条弦 AC，BD 相交于点 E，∠A=70o，∠c=50o，  °， C． 2 B． 3   1 2 D． 1 ，则 n 的值是（） 2 50 °，则 3 的度数等于（）那么 sin∠AEB 的值为( ) A. 1 2 B. 3 3 C. 2 2 D. 3 2 1 2 3 第 3 题第 4 题 5．某农机厂四月份生产零件 50 万个，第二季度共生产零件 182 万个.设该厂五、六月份平均每月的增长

率为 x，那么 x 满足的方程是（） A、 1(50  x ) 2  182 B． 50  1(50  x )  1(50  x ) 2  182 C、50(1+2x)＝182 D． 50  1(50  x )  )21(50 x   182 6．如图 6，在 ABCD 中，AB=6，AD=9，∠BAD 的平分线交 BC 于点 E，交 DC 的延长线于点 F，BG⊥AE，垂足为 G，BG= 24 ，则ΔCEF 的周长为（） A.8 B.9.5 C.10 D.11.5 得分评卷人 7．3 的绝对值是二填空题（每空 3 分，共 27 分） 8．1若 3 mx 2 5 y 与 3 x y 的和是单项式，则 mn  n ．。 9．据统计，去年我国粮食产量达 10570 亿斤，这个数用科学记数法可表示为 10．某校九年级（2）班（1）组女生的体重（单位：kg）为：38，40，35，36，65，42，42，则这组数据的中位数是亿斤．． 11．如图所示，AB∥CD，∠ABE＝66°，∠D＝54°，则∠E 的度数为_______________． 12．如图，已知双曲线 y ＞ k( )0 k x 经过直角三角形 OAB 斜边 OB 的中点 D，与直角边 AB 相交于点 C．若△ OBC 的面积为 3，则 k＝____________．第 11 题第 12 题 13．如图，已知零件的外径为 25 mm ，现用一个交叉卡钳（两条尺长 AC 和 BD 相等，OC=OD）量零件的内孔直径 AB．若 OC∶OA=1∶2，量得 CD＝10 mm ，则零件的厚度 _____ mm ．  x B C A

第 13 题第 14 题 14．如图 7，在 Rt ABC△ 部分的面积为 C ∠ 90 ．（结果保留  ）中，  °， AC  4 ， BC  2 ，分别以 AC . BC 为直径画半圆，则图中阴影 15．如下图是一组有规律的图案，第 1 个图案由 4 个基础图形组成，第 2 个图案由 7 个基础图形组成，……，第 n (n是正整数)个图案中由个基础图形组成． - 三解答题（本大题 8 个小题，共 75 分） (1) (2) …… (3) 得分评卷人 16．(8 分) 先化简再求值： ( x  x x   4 3 )  2 x x 4  3  ，其中 5 x  ．得分评卷人 17．（9 分）已知：如图，在等边三角形 ABC的 AC边上取中点 D，BC的延长线上取一点 E，使 CE ＝ CD．求证：BD ＝ DE．

得分评卷人 18．（9 分）在“首届中国西部（银川）房·车生活文化节”期间，某汽车经销商推出 A B C D 、、、四种型号的小轿车共 1000 辆进行展销．C 型号轿车销售的成交率为 50%，其它型号轿车的销售情况绘制在图 1 和图 2 两幅尚不完整的统计图中．（1）参加展销的 D 型号轿车有多少辆？（2）请你将图 2 的统计图补充完整；（3）通过计算说明，哪一种型号的轿车销售情况最好？（4）若对已售出轿车进行抽奖，现将已售出 A B C D 从中随机抽取一张，求抽到 A 型号轿车发票的概率．、、、四种型号轿车的发票（一车一票）放到一起，得分评卷人 19．（9 分）为申办 2010 年冬奥会，须改变哈尔滨市的交通状况。在大直街拓宽工程中，要伐掉一棵树 AB，在地面上事先划定以 B为圆心，半径与 AB等长的圆形危险区，现在某工人站在离 B点 3 米远的 D处，从 C 点测得树的顶端 A点的仰角为 60°，树的底部 B点的俯角为 30°. 问：距离 B点 8 米远的保护物是否在危险区内？9 分 A 60 30 C D B 得分评卷人 20．（9 分）如图， Rt ABC△ 中，点 D ，过点 D 的切线交 BC 于 E ． ABC  °，以 AB 为直径的 O⊙ 交 AC 于 90 （1）求证： DE  BC ； 1 2 （2）若 tan C  5 2 ， DE 2 ，求 AD 的长．

得分评卷人 21．（10 分）．如图，在正方形 ABCD中，点 E、F分别在 BC、CD上移动，但 A到 EF的距离 AH始终保持与 AB长相等，问在 E、F移动过程中：（1）∠EAF的大小是否有变化？请说明理由．（2）△ECF的周长是否有变化？请说明理由．得分评卷人 22．（10 分）某汽车制造厂开发了一款新式电动汽车，计划一年生产安装 240 辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人；他们经过培训后上岗，也能独立进行电动汽车的安装。生产开始后，调研部门发现：1 名熟练工和 2 名新工人每月可安装 8 辆电动汽车；2 名熟练工和 3 名新工人每月可安装 14 辆电动汽车。（1）每名熟练工和新工人每月分别可以安装多少辆电动汽车？（2）如果工厂招聘 n（0

得分评卷人 23．（11 分）已知：等边三角形 ABC 的边长为 4 厘米，长为 1 厘米的线段 MN 在的边 AB 上沿 AB 方向以 1 厘米/秒的速度向 B 点运动（运动开始时，点 ABC△ M 与点 A 重合，点 N 到达点 B 时运动终止），过点 M N、分别作 AB 边的垂线，与 ABC△ 的其它边交于 P Q、两点，线段 MN 运动的时间为t 秒．（1）线段 MN 在运动的过程中，t 为何值时，四边形 MNQP 恰为矩形？并求出该矩形的面积；（2）线段 MN 在运动的过程中，四边形 MNQP 的面积为 S ，运动的时间为t ．求四边形 MNQP 的面积 S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围． C Q P A M N B C P Q A M N B

C Q P A M N B

分享到：

赞收藏

资料库

2010年湖南省衡阳市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料