logo资料库

论文研究-一种新的自适应惯性权重混沌PSO算法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.69M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    Computer Engineering and Applications 计算机工程与应用 2018，54（9） 139 一种新的自适应惯性权重混沌 PSO 算法 李龙澍 1，2，张效见 2 LI Longshu1，2, ZHANG Xiaojian2 1. 安徽大学 计算智能与信号处理教育部重点实验室，合肥 230039 2. 安徽大学 计算机科学与技术学院，合肥 230601 1.Key Laboratory of Intelligent Computing and Signal Processing, Anhui University, Hefei 230039, China 2.School of Computer Science and Technology, Anhui University, Hefei 230601, China LI Longshu, ZHANG Xiaojian. New chaos particle swarm optimization based on adaptive inertia weight. Computer Engineering and Applications, 2018, 54（9）：139-144. Abstract：Particle Swarm Optimization（PSO）is easy to fall into the local optimal value. According to this disadvantage, a New Chaos Particle Swarm Optimization based on Adaptive Inertia Weight（CPSO-NAIW）is proposed. Firstly, the new inertia weight adaptive method is used to make a balance between the global and local search of the particles. It can reduce the probability of particles trap in local optimal. Then, when the algorithm falls into local optimal value, the strategy of chaos optimization is introduced to adjust the position of the population’s extreme value so that the particles can search the new neighorhood and path. The probability of getting rid of the local extremum is increaseed. Finally, the experimental results show that the CPSO-NAIW algorithm can avoid the local optimal and improve the performance of the algorithm effectively. Key words：particle swarm optimization; adaptive inertia weight; chaos; local extreme value 摘 要：针对粒子群算法（Particle Swarm Optimization，PSO）易陷入局部极值的缺陷，提出了一种新的自适应惯性 权重混沌 PSO 算法（a New Chaos Particle Swarm Optimization based on Adaptive Inertia Weight，CPSO-NAIW）。首 先采用新的惯性权重自适应方法，很好地平衡粒子的搜索行为，减少算法陷入局部极值的概率，然后在算法陷入局 部极值时，引入混沌优化策略，对群体极值位置进行调整，以使粒子搜索新的邻域和路径，增加算法摆脱局部极值的 可能。最后，实验结果表明，CPSO-NAIW 算法能有效避免陷入局部极值，提高算法性能。 关键词：粒子群 ；自适应惯性权重 ；混沌 ；局部极值 文献标志码：A 中图分类号：TP301.6 doi：10.3778/j.issn.1002-8331.1612-0093 1 引言 PSO 算法是一种寻优算法，于 1995 年由 Eberhart 和 Kennedy 首次提出 [1-2]。它源于模拟鱼类和鸟类的寻食 行为[3]。PSO 算法具有操作简单、鲁棒性强和易于实现 等优点，优化性能较好，常用于解决多峰值、不可微和非 线性等问题，并在工程和科学领域得到广泛应用，如函 数优化[4]、排列[5]和神经网络[6]等。 虽然 PSO 算法优化性能较好，但是在寻优求解进程 中，不能很好地平衡粒子的搜索行为，存在易陷入局部 极值的缺陷。对此，研究人员提出了诸多改进方法，主 要分为以下两类：第一类是在 PSO 算法速度迭代公式中 增加惯性权重 ω ，以更好地平衡粒子的搜索行为。近年 来，研究人员对惯性权重进行了广泛研究[7-10]。例如，文 献[7-8]提出惯性权重线性减少方法，以提高寻优性能， 并被广泛应用，称之为标准 PSO 算法。但在该算法中， 如果粒子在寻优初期搜索到的位置不够好，易陷入局部 极值。文献[9-10]对惯性权重采用指数减少方法，减少 了算法陷入局部极值的概率。另一类是引入其他优化 基金项目：青年科学基金项目（No.61402005）。 作者简介：李龙澍（1956—），男，教授，博士生导师，研究领域为智能软件、不精确信息处理技术，E-mail：lilongshu@126.com；张效 见（1990—），男，硕士研究生，研究领域为机器博弈。 收稿日期：2016-12-07 修回日期：2017-01-23 文章编号：1002-8331（2018）09-0139-06 CNKI 网络出版：2017-04-01, http://kns.cnki.net/kcms/detail/11.2127.TP.20170401.0839.016.html 计算机工程与应用www.ceaj.org
    140 2018，54（9） Computer Engineering and Applications 计算机工程与应用 方法，文献[11]在 PSO 算法中引入两种混沌优化策略， 提高了收敛精度。文献[12]在 PSO 算法中引入 GA 算法 的变异和交叉操作，提高了收敛性。基于以上研究，本 文针对 PSO 算法易陷入局部极值的缺陷，提出了一种新 的自适应惯性权重混沌 PSO 算法（a New Chaos Particle Swarm Optimization based on Adaptive Inertia Weight， CPSO-NAIW）。实验结果表明，CPSO-NAIW 算法能有 效避免陷入局部极值，提高算法性能。 2 PSO 算法 PSO 算法可具体表述如下：首先初始化种群粒子， 然后每一个粒子通过追逐个体和群体极值位置，即粒子 本身和整个粒子种群当前找到最优解的位置，来更新粒 子的位置和速度，最后不断迭代直到找到在指定阈值的 最优位置。在种群规模为 M ，解空间为 D 维的 PSO 算 法中，设第 i 粒子个体和群体极值位置分别为 Pi 和 G ， 在 d 维的位置和速度分别为 xid 和 vid ，xid 和 vid 的更 新公式如下： id + c1r1( id = ωt i vt vt + 1 （1） id = x t id + vt + 1 x t + 1 （2） id 其中，ωt i 为第 i 个粒子在 t 代中的惯性权重；t 为当前 代数；i = 1,2,…,M ；d = 1,2,…,D ；r1 和 r2 为服从 )0,1 分布的随机数；学习因子 c1 和 c2 为非负常数，通 U( 常取值为 c1 = c2 = 2 ；vid ∈ [ -νmax,vmax ，vmax 为速度最 大值，是由用户设定的常数。 Pid - xid + c2r2( Gd - xid ] ) ) 在 PSO 算法中，惯性权重 ωt i 至关重要，被用于平衡 粒子的搜索行为。适当的惯性权重调整方法，将可以减 少算法陷入局部极值的概率[13]。另外，当算法陷入局部 极值时，种群粒子在局部极值位置附近聚集并重复类似 的寻优轨迹，导致算法很难摆脱局部极值[14-15]。因此本 文提出了 CPSO-NAIW 算法。该算法从惯性权重的调 整以及如何摆脱局部极值两个方面入手来改善 PSO 算 法的性能。 3 CPSO-NAIW 算法 介绍了惯性权重线性减少方法的缺点，然后提出了 一种根据粒子与群体极值位置距离进行权重调整的方 法，该方法更好地平衡了粒子的搜索行为，减少了算法 陷入局部极值的概率，最后针对算法如何摆脱局部极值 的问题，提出了一种基于混沌优化摆脱局部极值的方 法，该方法通过引入混沌优化策略，在算法陷入局部极 值时，对群体极值位置进行调整，以使粒子经历新的搜 索邻域和路径，增加算法摆脱局部极值的可能。 3.1 自适应惯性权重 在 PSO 算法寻优迭代中，应用较多的是惯性权重线 性减少方法，然而，PSO 算法的寻优进程是非线性且十 分复杂的，线性减少的方法变化过于单一，造成其对非 线性、复杂寻优进程的调节和适应能力有限，易陷入局 部极值。因此，本文提出了一种新的惯性权重自适应方 法（New Adaptive Inertia Weight，NAIW），NAIW 计算 方法如式（3）所示。 （3） （4） Δxt i + ωmin ωt i = k × ωmax - ωmin max{ }Δxt i Δxi = ∑ D ( k = iterNum - t iterNum xid - Gd d = 1 ) 2 （5） 其中，ωmax 和 ωmin 分别为惯性权重的最大和最小值， ωmax =0.9，ωmin =0.4[16]；Δxi 为第 i 个粒子与群体极值位 i 为 Δxi 在 t 代中的 置的距离，利用式（4）计算得到；Δxt 值；iterNum 为最大迭代次数；k 为迭代系数，利用式 （5）计算得到。NAIW 方法通过粒子相对于群体极值位 置的距离对权重进行动态调整，把权重的变化与粒子的 位置状态信息关联起来，以更加精确地调整惯性权重。 当 Δxt i 较大时，即粒子距当前最优解位置的距离较远， 则利用式（3）会赋予速度更新式（1）中 ωt i 较大的值，以 使粒子获得较大飞行速度，进而可以使其更快速地向当 前最优解位置靠近并保证了种群全局“探索”能力，当 Δxt i 较小时，即粒子距当前最优解位置的距离较近，则 利用式（3）会赋予速度更新式（1）中 ωt i 较小的值，以使 粒子获得较小飞行速度，进而可以使其更加精细地搜索 最优解位置邻域，保证了种群局部“开发”能力。同时， 式（3）中的 k 值随迭代次数的增加而减少，以保证算法 在迭代初期和后期分别对较大和较小 ωt i 的需要[7-8]。通 过以上调整权重的方法，增强了权重的自适应性，更好 地平衡了粒子的搜索行为，减少了算法陷入局部极值的 概率，提高了 PSO 算法的收敛性。 3.2 基于混沌优化摆脱局部极值的方法 混沌是一种非线性的自然现象，具有随机性、遍历 性等特点，可进行寻优搜索[17-19]。 ) ) t + 1 一个常用的混沌模型 Logistic 方程如下： zn + 1 = μzn( 1 - zn ,n = 0,1,2,… （6） 其 中 ，μ 为 控 制 参 量 ，当 0 ≤ z0 ≤ 1 ，μ = 4 时 ，Logistic 处于完全混沌状态。式（7）为 Logistic 方程的一种演化 形式[20]。 Cx ( i Cxi = ( i = a + Cxi( x' （7） （8） （9） i 为 混 沌 变 量 Cxi 在 第 t 次 迭 代 后 的 值 ；当 其 中 ，Cx t Cxi ∈ [ 0.25,0.5,0.75 时 ，将 产 生 混 沌 现 象 [20]。 解 空 间 变 量 xi ∈ [ ]a,b 可 通 过 式（8）和 式（9）与 Cxi 进行往返映射；a 和 b 分别为解空间的最大和最小 i( = 4Cx t ) xi - a /( b - a 1 - Cx t ) b - a ) ) i , i = 0,1,2,… ]0,1 且 Cxi ∉ { } 计算机工程与应用www.ceaj.org
    李龙澍，张效见：一种新的自适应惯性权重混沌 PSO 算法 2018，54（9） 141 值；x' i 为 xi 混沌优化后得到的在解空间中的新值。 本文借鉴混沌现象随机性和遍历性的特点，提出了 基于混沌优化摆脱局部极值的方法。该方法通过群体 极值位置连续未更新的代数 SG 与局部极值判定阈值 SGmax 进行比较来判定算法是否陷入局部极值 [14]。若 SG ≥ SGmax ，则认为算法已经或即将陷入局部极值；反 之，则认为算法没有陷入局部极值。当算法被判定为陷 入局部极值时，首先利用式（8）把群体极值位置 G 映射 到混沌变量定义域 [ ]0,1 内，然后利用式（7）进行迭代运 算，得到 M 个混沌位置 (CG1,CG 2,CG 3,…,CG m) ，最后 利 用 式（9）进 行 逆 映 射 ，获 得 M 个 新 群 体 极 值 位 置 （ G1' ,G 2' ,G 3' ,…,G m' ）。由于粒子通过追逐个体和群体 极值位置来完成自我更新，当算法陷入局部极值时，群 体极值位置一定在局部极值位置上，此时，采用混沌映 射得到具有较强随机性和遍历性的新群体极值位置，并 结合式（1）就可以改变粒子的寻优轨迹，使得粒子 i 通 过追逐新群体极值位置 G i' 进行自我更新时，可在局部 极值位置邻域外的其他区域进行寻优搜索，搜索新的邻 域和路径。因此可以较大概率地发现更优解，进而增加 了算法摆脱局部极值的可能。 3.3 CPSO-NAIW 算法执行流程 本文从惯性权重的调整和如何摆脱局部极值两个 方面对 PSO 算法进行改进，提出了 CPSO-NAIW 算法， 该算法的具体执行流程如下。 输入：算法迭代次数 T 、种群规模 M 。 输出：最优位置 G 。 （1）随机初始化种群中粒子的速度和位置，初始化 迭代次数、计数器和局部极值判定阈值为 t = 0 、SG = 0 和 SGmax =10[14]。 （2）初始化 P 为粒子当前位置，G 为初始群体最优 粒子位置。 （3）对种群中所有粒子执行以下操作： ① 根据式（3）更新粒子的权重 ωt i 。 ② 根据式（1）和式（2）更新粒子速度和位置。 ③ 计算粒子适应度值 f ，并更新粒子的 P 和 G ， 如果 G 未更新，SG = SG + 1 ，否则 SG = 0 。 （4）如果 SG ≥ SGmax ，利用式（7）~（9）对 G 进行混 沌优化生成 G1' ,G2' ,Gi' ,…,Gm' ，SG = 0 。 （5）t = t + 1 ，如果 t < T ，转（3），否则，执行（6）。 （6）输出 G ，算法结束。 在 CPSO-NAIW 算法中，第（1）、（2）步对算法各个 参数进行初始化，第（3）~（6）步对求解问题进行寻优搜 索。其中，第（3）步利用本文提出的新惯性权重自适应 方法（NAIW）对粒子进行更新，第（4）步判断算法是否 陷入局部极值，若 SG ≥ SGmax ，则认为算法已经或即将 陷入局部极值，并利用本文提出的基于混沌优化摆脱局 部极值的方法来进行摆脱。 4 实验结果与分析 首先介绍了实验环境和算法参数设置，然后为了验 证本文提出的改进方法的有效性，采用 6 个经典基准函 数对算法性能进行测试。基准函数信息见表 1。并设计 如下方案进行对比。方案 1：对两种改进方法分开进行 测试，首先在标准 PSO 算法 [7]（Standard Particle Swarm Optimization，SPSO）即线性减少惯性权重 PSO 算法的 基础上，对权重的调整采用本文提出的新自适应惯性权 重方法，形成 PSO-NAIW 算法，然后在 SPSO 算法基础 上，加入本文提出的基于混沌摆脱局部极值方法，形成 CPSO 算法，最后把本文提出的两种改进方法综合起来， 形成 CPSO-NAIW 算法并把它们与 SPSO 算法进行对 比测试。方案 2：为展示本文 CPSO-NAIW 算法的先进 性，将 CPSO-NAIW 算法与一些具有代表性的新近改进 PSO 算法，即 IAW-PSO[21]、高速收敛 PSO 算法（表示为 FPSO）[14]、PDNPO-PSO算法[22]和SPSO算法进行对比测试。 4.1 实验环境与参数设置 实验采用 C#编写，实验环境为（M490）CPU 3.20 GHz 表 1 基准函数 函数名 Sphere f1 Schwefel f2 f2( 函数表达式 )x = ∑ D x2 f1( )x = ∑ i = 1 | D i Ackley f3 f3( )x = -20 exp æ çç è Shaffer f4 f4( -0.2 ∑ )x = 0.5 + Exponential f5 Duadric f6 f5( cos 2πxi D + 20 + e ö ÷÷ ø | xi | i = 1 D i = 1 | xi + ∏ ö ÷÷ ø i = 1 D i = 1 ∑ ) x2 + y2 i D - expæ D x2 çç è ( sin2 x2 + y2 - 0.5 ) 1.0 + 0.001( ) -0.5∑ D x2 ( 2 ö ÷ ø i )x = -expæ ç è )x = ∑ D æ çç è f6( i = 1 i = 1 2 ÷÷∑ ö D xj ø j = 1 搜索区间 理论极值 目标精度 [－100，100]30 [－10，10]30 [－32，32]30 [－100，100]2 [－1，1]30 [－100，100]30 0 0 0 0 -1 0 10－2 10－2 10－2 10－2 10－2 10－2 计算机工程与应用www.ceaj.org
    142 2018，54（9） Computer Engineering and Applications 计算机工程与应用 Inter core i5 和 4 GB RAM。PSO-NAIW、CPSO、CPSO- NAIW 以及 SPSO 算法参数设置如下：惯性权重最大和 最小值分别为 ωmax =0.9 和 ωmin =0.4；IAW-PSO 算法参 数设置如下[21]：惯性权重最大和最小值分别为 ωmax =0.9 和 ωmin =0.2；迭代步数 K1 =60，K2 =10；最大初始化次数 kmax =200；FPSO 算法参数设置如下[14]：惯性权重最大和 最小值分别为ωmax =0.9 和 ωmin =0.4；停滞上限 MAX=10； PDNPO-PSO 算法参数设置如下 [22]：惯性权重最大和最 小值分别为 ωmax =0.9 和 ωmin =0.4；惯性权重取值范围中 间值 ωs =0.65；上限控制参数 k1 = 2 ；调节能力控制参数 k2 = 1 ；个体学习因子的最大和最小值分别为 c1 max = 2 和 c1 min = 0 ；群体学习因子的最大和最小值分别为 c2 max = 2 和 c2 min = 0 ；振荡周期 L = 300 。所有算法的种群规模 M 为 30；学习因子 c1 = c2 = 2 。 4.2 PSO-NAIW、CPSO、CPSO-NAIW 和 SPSO 算法对比测试 为了测试 PSO-NAIW、CPSO 和 CPSO-NAIW 算法 性能，本文设置以下实验进行对比分析。 实 验 1 PSO- NAIW、CPSO、CPSO- NAIW 和 SPSO 算法在迭代 1 000 次的情况下，对 6 个基准函数进行寻 优搜索，每个算法进行 20 次独立实验，取各个函数最终 结果的平均（Mean）和最优（Opt）值进行比较。实验结 果如表 2 所示。 实 验 2 PSO- NAIW、CPSO、CPSO- NAIW 和 SPSO 算法在固定目标精度下（各个函数目标精度如表 1），对 6 个基准函数进行寻优搜索，每个算法进行 20 次独立实 验，取各个算法达到目标精度时的平均迭代次数 (Itr) 、 平均运行时间 (t) 及收敛率 (CR) 。其中，收敛率=达到 目标精度次数/总实验次数。算法 2 000 次迭代内不收 敛即视为当次实验失败，实验结果如表 3 所示。 从表 2 中看出，虽然 PSO-NAIW、CPSO 和 CPSO- NAIW 算法在对函数 f4 和 f5 测试时，与 SPSO 算法实验 结果相同，但是在其他 4 个函数上无论是最优还是平均 函数值都明显优于 SPSO 算法，并且 CPSO-AIW 算法实 验结果最优。从表 3 中看出，虽然 PSO-NAIW、CPSO 和 CPSO-NAIW 算法在对函数 f1 ~ f5 测试时，与 SPSO 算 法的收敛率相同，但是 PSO-NAIW 和 CPSO 算法对于除 函数 f4 外的其他 4 个函数，收敛速度更快、用时较少，并 且，CPSO-NAIW 算法对函数 f1 ~ f5 的收敛速度最快、 用 时 最 少 。 同 时 在 表 3 中 还 可 以 看 出 ，PSO-NAIW、 CPSO 和 CPSO-NAIW 算法在对函数 f6 进行测试时，这 三种算法相对于 SPSO 算法的收敛率更高、收敛速度更 快、运行时间更短，并且 CPSO-NAIW 算法的收敛率最 高、收敛速度最快、运行时间最短。综上，可以得出， PSO-NAIW、CPSO 和 CPSO-NAIW 算法在整体性能上 优于 SPSO 算法。这是因为 PSO-NAIW 算法根据粒子 与群体极值位置距离来调整惯性权重，改善了权重的自 适应性，更好地平衡种群的局部“开发”和全局“探索”能 力，降低了算法陷入局部极值的可能。所以，算法用时 较少、收敛精度和速度明显提高。CPSO 算法利用混沌 现象随机性及遍历性的特点，在算法陷入局部极值时， 对群体极值位置进行混沌优化，以使粒子搜索局部极值 外的新邻域和新路径，增强了算法跳出局部极值的可 能。所以，算法运行时间短、收敛精度高且速度快。而 CPSO-NAIW 算法综合了 PSO-NAIW 和 CPSO 算法的改 进方法，所以具有最优的收敛性能。 4.3 CPSO-NAIW、IAW-PSO、FPSO、PDNPO- PSO 和 SPSO 算法对比测试 为了验证本文 CPSO-NAIW 算法性能，在 6 个基准 函数上对本文 CPSO-NAIW 与 IAW-PSO、PDNPO-PSO、 表 2 实验 1 结果 测试函数 f1 f2 f3 f4 f5 f6 SPSO PSO-AIW CPSO CPSO-NAIW Opt Mean Opt Mean Opt Mean Opt Mean 9.933 3E-14 1.600 1E-09 1.851 3E-08 1.021 5E-11 2.424 9E-08 4.605 5E-07 3.161 7E-25 1.024 0E-16 2.886 5E-12 1.208 6E-20 1.699 5E-15 4.414 2E-12 5.855 1E-18 8.313 8E-12 2.176 0E-16 1.710 0E-14 1.580 0E-10 1.712 2E-11 1.512 7E-32 1.074 1E-19 7.543 7E-17 1.338 9E-28 2.818 3E-17 1.659 5E-14 0 -1 0 -1 0 -1 0 -1 0 -1 0 -1 0 -1 0 -1 0.000 2 5.807 2 2.493 7E-05 0.059 1 2.440 9E-05 0.035 1 6.341 2E-7 0.018 6 测试函数 f1 f2 f3 f4 f5 f6 SPSO t/ms 1 516.57 1 128.81 1 943.74 1.73 1 332.43 3 538.57 Itr 695 685 735 10 608 1 116 表 3 实验 2 结果 PSO-NAIW CR 1 1 1 1 1 0.55 Itr 248 282 324 6 148 592 t/ms 667.04 497.31 1 053.64 2.10 390.72 2 261.47 CR 1 1 1 1 1 0.70 Itr 435 513 379 8 347 473 CPSO t/ms 1 117.95 878.51 1 140.79 2.64 891.79 1 716.93 CPSO-NAIW CR 1 1 1 1 1 0.75 Itr 167 203 261 4 109 423 t/ms 346.98 375.55 1 025.73 1.56 334.63 1 696.23 CR 1 1 1 1 1 0.80 计算机工程与应用www.ceaj.org
    李龙澍，张效见：一种新的自适应惯性权重混沌 PSO 算法 2018，54（9） 143 SPSO CPSO-NAIW FPSO PDNPO-PSO IAW-PSO 0 1 2 5 4 3 7 进化迭代次数/102 6 8 9 10 图 3 f3 函数 SPSO CPSO-NAIW FPSO PDNPO-PSO IAW-PSO 0 1 2 8 9 10 6 5 4 3 7 进化迭代次数/102 图 6 10 0 -10 -20 -30 ) ) x ( f ( g l SPSO CPSO-NAIW FPSO PDNPO-PSO IAW-PSO SPSO CPSO-NAIW FPSO PDNPO-PSO IAW-PSO 15 10 5 0 5 -10 -15 -20 ) ) x ( f ( g l 0 1 2 8 9 10 0 1 2 5 4 3 7 进化迭代次数/102 6 4 5 3 7 进化迭代次数/102 6 8 9 10 图 1 f1 函数 SPSO CPSO-NAIW FPSO PDNPO-PSO IAW-PSO 0.20 0.15 0.10 0.05 ) x ( f 均 平 0 1 2 5 4 3 7 进化迭代次数/102 6 8 9 10 图 2 f2 函数 SPSO CPSO-NAIW FPSO PDNPO-PSO IAW-PSO 0 1 2 5 4 7 3 进化迭代次数/102 6 8 9 10 0 -0.2 -0.4 -0.6 -0.8 -1.0 -1.2 ) x ( f 均 平 5 0 5 -10 -15 ) ) x ( f ( g l 3 2 1 0 -1 -2 ) ) x ( f ( g l 图 4 f4 函数 图 5 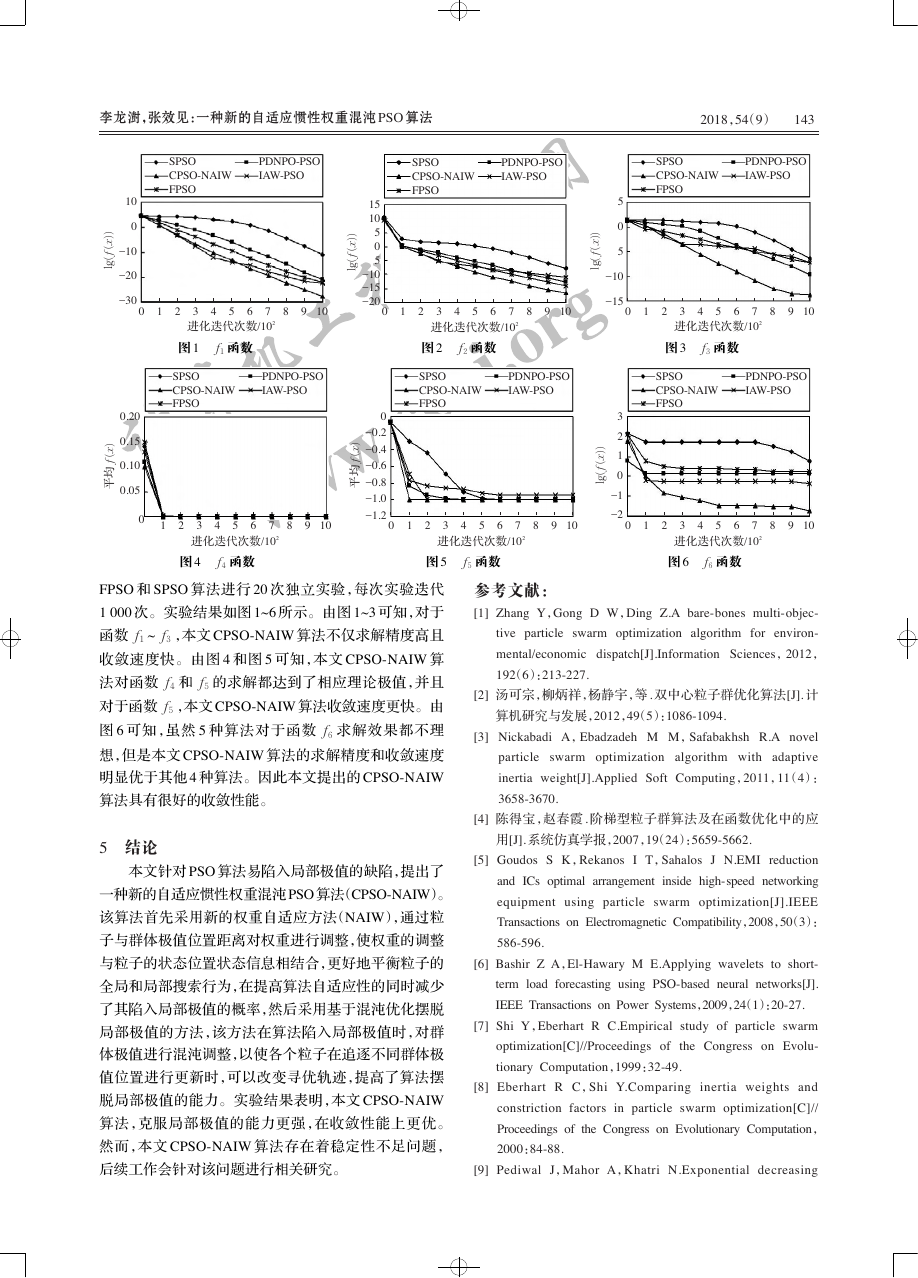FPSO 和 SPSO 算法进行 20 次独立实验，每次实验迭代 1 000 次。实验结果如图 1~6 所示。由图 1~3 可知，对于 函数 f1 ~ f3 ，本文 CPSO-NAIW 算法不仅求解精度高且 收敛速度快。由图 4 和图 5 可知，本文 CPSO-NAIW 算 法对函数 f4 和 f5 的求解都达到了相应理论极值，并且 对于函数 f5 ，本文 CPSO-NAIW 算法收敛速度更快。由 图 6 可知，虽然 5 种算法对于函数 f6 求解效果都不理 想，但是本文 CPSO-NAIW 算法的求解精度和收敛速度 明显优于其他 4 种算法。因此本文提出的 CPSO-NAIW 算法具有很好的收敛性能。 5 结论 本文针对 PSO 算法易陷入局部极值的缺陷，提出了 一种新的自适应惯性权重混沌 PSO 算法（CPSO-NAIW）。 该算法首先采用新的权重自适应方法（NAIW），通过粒 子与群体极值位置距离对权重进行调整，使权重的调整 与粒子的状态位置状态信息相结合，更好地平衡粒子的 全局和局部搜索行为，在提高算法自适应性的同时减少 了其陷入局部极值的概率，然后采用基于混沌优化摆脱 局部极值的方法，该方法在算法陷入局部极值时，对群 体极值进行混沌调整，以使各个粒子在追逐不同群体极 值位置进行更新时，可以改变寻优轨迹，提高了算法摆 脱局部极值的能力。实验结果表明，本文 CPSO-NAIW 算法，克服局部极值的能力更强，在收敛性能上更优。 然而，本文 CPSO-NAIW 算法存在着稳定性不足问题， 后续工作会针对该问题进行相关研究。 f6 函数 f5 函数 参考文献： [1] Zhang Y，Gong D W，Ding Z.A bare-bones multi-objec- tive particle swarm optimization algorithm for environ- mental/economic dispatch[J].Information Sciences，2012， 192（6）：213-227. [2] 汤可宗，柳炳祥，杨静宇，等 . 双中心粒子群优化算法[J]. 计 算机研究与发展，2012，49（5）：1086-1094. [3] Nickabadi A，Ebadzadeh M M，Safabakhsh R.A novel particle swarm optimization algorithm with adaptive inertia weight[J].Applied Soft Computing，2011，11（4）： 3658-3670. [4] 陈得宝，赵春霞 . 阶梯型粒子群算法及在函数优化中的应 用[J]. 系统仿真学报，2007，19（24）：5659-5662. [5] Goudos S K，Rekanos I T，Sahalos J N.EMI reduction and ICs optimal arrangement inside high-speed networking equipment using particle swarm optimization[J].IEEE Transactions on Electromagnetic Compatibility，2008，50（3）： 586-596. [6] Bashir Z A，El-Hawary M E.Applying wavelets to short- term load forecasting using PSO-based neural networks[J]. IEEE Transactions on Power Systems，2009，24（1）：20-27. [7] Shi Y，Eberhart R C.Empirical study of particle swarm the Congress on Evolu- optimization[C]//Proceedings of tionary Computation，1999：32-49. [8] Eberhart R C，Shi Y.Comparing inertia weights and constriction factors in particle swarm optimization[C]// Proceedings of the Congress on Evolutionary Computation， 2000：84-88. [9] Pediwal J，Mahor A，Khatri N.Exponential decreasing 计算机工程与应用www.ceaj.org
    144 2018，54（9） Computer Engineering and Applications 计算机工程与应用 inertia weight particle swarm optimization in economic load dispatch[J].International Journal of Engineering Innovations & Research，2012，1（5）：380-384. [10] Ting T O，Shi Y，Cheng S，et al.Exponential inertia for particle swarm optimization[C]//International weight Conference in Swarm Intelligence，2012：83-90. [11] 刘道华，原思聪，兰洋，等 . 混沌映射的粒子群优化方法[J]. 西安电子科技大学学报：自然科学版，2010，37（4）：764-769. [12] 雷秀娟，付阿利，孙晶晶，等 . 改进 PSO 算法的性能分析与 研究[J]. 计算机应用研究，2010，27（2）：453-458. [13] 丁旭，吴晓蓓，黄成 . 基于改进粒子群算法和特征点集的 无线传感器网络覆盖问题研究[J]. 电子学报，2016，44 （4）：967-973. [14] 朱海梅，吴永萍 . 一种高速收敛粒子群优化算法[J]. 控制 与决策，2010，25（1）：20-24. [15] 吕振肃，侯志荣 . 自适应变异的粒子群优化算法[J]. 电子 学报，2004，32（3）：416-420. [16] 敖永才，师奕兵，张伟，等 . 自适应惯性权重的改进粒子群 算法[J]. 电子科技大学学报，2014，43（6）：874-880. [17] Ying Song，Chen Zengqiang，Yuan Zhuzhi.New chaotic PSO-based neural network predictive control for non- linear process[J].IEEE Transactions on Neural Networks， 2007，18（2）：595-601. [18] Zhou Keliang，Qin Jieqiong.PID controller parameters tuning of main steam temperature based on chaotic particle swarm optimization[C]//IEEE International Con- ference on Computer Science and Automation Engi- neering（CSAE），2011：647-650. [19] 唐贤伦，周维，张衡，等 . 一种基于多目标混沌 PSO 的机器 人足球防守策略[J]. 系统仿真学报，2014，26（1）：51-55. [20] 莫愿斌，陈德钊，胡上序，等 . 混沌粒子群算法及其在生化 过程动态优化中的应用[J]. 化工学报，2006，57（9）：2123- 2127. [21] 杜继永，张凤鸣，李建文，等 . 一种具有初始化功能的自适 应惯性权重粒子群算法[J]. 信息与控制，2012，41（2）： 165-169. [22] 朱喜华，李颖晖，李宁，等 . 基于群体早熟程度和非线性周 期振荡策略的改进粒子群算法[J]. 通信学报，2014，35 （2）：182-189. （上接 108 页） [17] Bird S.NLTK：The natural language toolkit[C]//Proceed- ings of the COLING/ACL on Interactive Presentation sessions.Association for Computational Linguistics，2006： 69-72. [18] Willett P.The Porter stemming algorithm：Then and now[J]. Program，2006，40（3）：219-223. [19] Bao P，Jackson T J，Wang X，et al.Barium strontium titanate thin film varactors for room-temperature micro- wave device applications[J].Journal of Physics D：Applied Physics，2008，41（6）. analysis of culture using millions of digitized books[J]. Science，2011，331：176-182. [21] Web language model API[EB/OL].（2016）.https：//goo.gl/ m0WNP7. [22] Groups G.VirusTotal-Free online virus，malware and URL scanner[EB/OL].（2016）.https：//www.virustotal.com. [23] urlQuery-Free URL scanner[EB/OL].（2016）.https：//urlquery.net/. [24] Vadrevu P，Rahbarinia B，Perdisci R，et al.Measuring and detecting malware downloads in live network traffic[C]//European Symposium on Research in Computer Security（ESORICS 2013），2013：556-573. [25] Malicious corpus for extracting domains[EB/OL].（2016）. [20] Michel J B，Shen Y K，Aiden A P，et al.Quantitative https：//github.com/ourren/malicious_corpus. （上接 132 页） [10] 彭敏，高斌龙，黄济民，等 . 基于高质量信息提取的微博自 动摘要[J]. 计算机工程，2015，41（7）：36-42. [11] Dong Z D，Dong Q，Hao C.HowNet and its computation of meaning[C]//Proceedings of the 23rd International Conference on Computational.Linguistics（COLING’10）， New York，2010：53-56. [12] 刘杰，郭宇，汤世平 . 基于知网 2008 的词语相似度计算[J]. 小型微型计算机系统，2015，36（8）：1729-1734. [13] Parikh R，Karlapalem K.ET：Events from tweets[C]// International Conference on World Wide Web Companion. New York：ACM，2013：613-620. [14] Poomagal S，Visalakshi P，Hamsapriya T.A novel method for clustering tweets in Twitter[J].International Journal of Web Based Communities，2015，11（2）：170-187. [15] 朱明峰，叶施仁，叶仁明 . 基于 Lex-PageRank 的微博摘要 优化方法[J]. 计算机科学，2016，43（9）：261-265. [16] Milhalces R，Tarau P.TextRank：Bringing order into texts[C]// Association for Computational Linguistics，Barcelona，Spain， 2004：118-126. [17] 余珊珊，苏锦钿，李鹏飞 . 基于改进的 TextRank 的自动摘 要提取方法[J]. 计算机科学，2016，43（6）：240-247. [18] 席耀一，李弼程，李天彩，等 . 基于词语对狄利克雷过程的 时序摘要[J]. 自动化学报，2015（8）：1452-1460. 计算机工程与应用www.ceaj.org
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料