第1页 / 共20页
第2页 / 共20页
第3页 / 共20页
第4页 / 共20页
第5页 / 共20页
第6页 / 共20页
第7页 / 共20页
第8页 / 共20页
C++数据结构排序算法.docx
堆的插入
堆的删除
堆化数组
堆排序
常见的分类算法还可以根据排序方式分为两大类：比较排序和非比较排序。本文
中前七种算法都是比较排序，非比较排序有三种，分别为：
1）计数排序(Count Sort)（复杂度 O(n+k)（其中 k 是待排序的 n 个数字中
最大值）
2）基数排序(Bucket Sort)（复杂度 O(nk)（其中 k 是最大数字的位数）
3）桶排序(Radix Sort)（复杂度 O(n+k)（其中 k 是待排序的 n 个数字中最
大值）
非比较排序的特点是时间复杂度很低，都是线性复杂度 O(n)，但是非比较
排序受到的限制比较多，不是通用的排序算法。
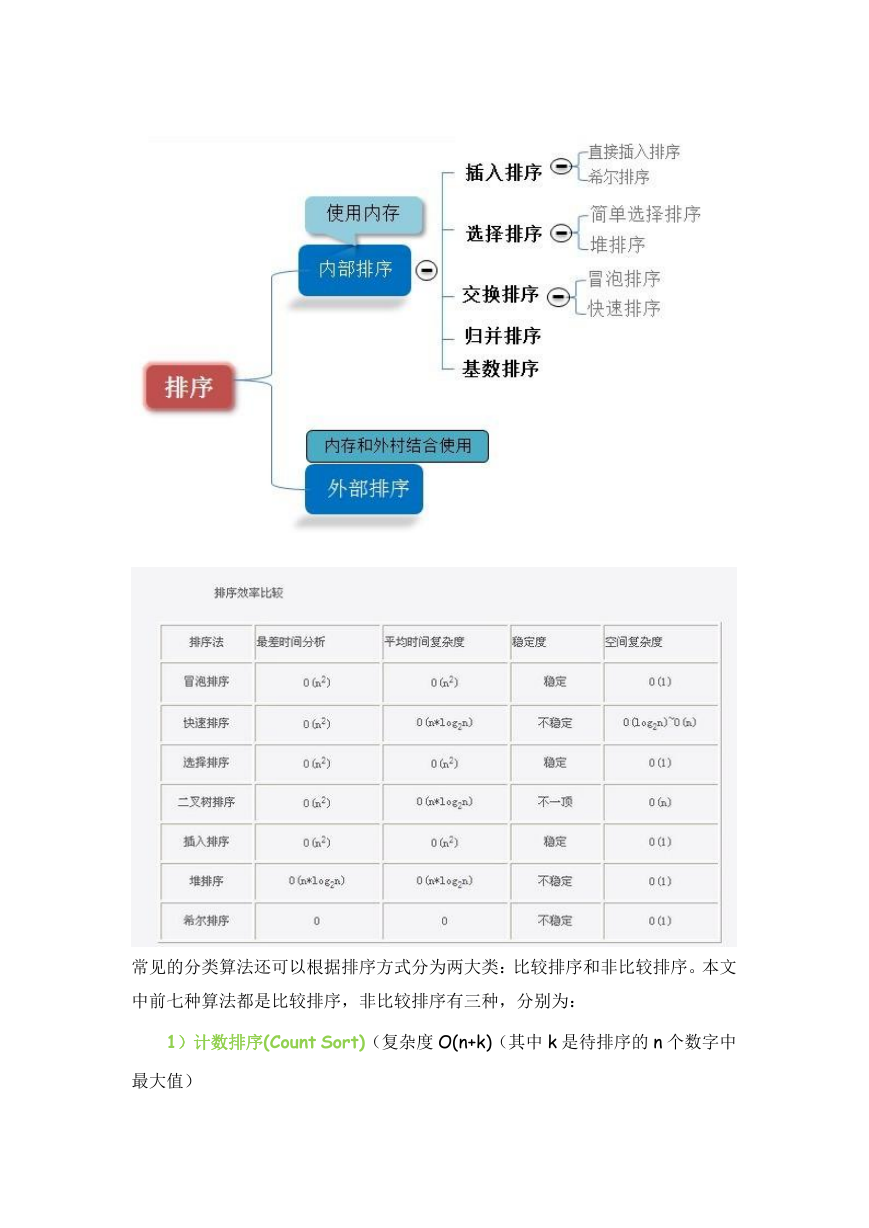
1. 直接插入排序（Straight Insertion Sort）
直接插入排序（Insertion Sort），是一种简单直观的排序算法。它的
工作原理是通过构建有序序列，对未排序的数据，在已排序序列中从后
向前扫描，找到相应位置并插入。
插入排序算法的一般步骤：
1.从第一个元素开始，该元素可以认为已被排序；
2.取出下一个元素，在已经排序的元素序列中从后向前扫描；
3.如果该元素（已排序）大于新元素，将该元素移到下一个位置；
4.重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置；
5.将新元素插入到该位置后，重复 2~5
#include
// 分类 ------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- 最坏情况为输入序列是降序排列的,此时时间复杂度 O(n^2)
// 最优时间复杂度 ---- 最好情况为输入序列是升序排列的,此时时间复杂度 O(n)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 稳定
void InsertionSort(int A[], int n)
{
for (int i = 1; i < n; i++)
// 类似抓扑克牌排序
{
int get = A[i];
int j = i - 1;
// 右手抓到一张扑克牌
// 拿在左手上的牌总是排序好的
while (j >= 0 && A[j] > get)
// 将抓到的牌与手牌从右向左进行比较
{
}
A[j + 1] = A[j];
// 如果该手牌比抓到的牌大，就将其右移
j--;
A[j + 1] = get; // 直到该手牌比抓到的牌小(或二者相等)，将抓到的牌插入到该手牌右边
(相等元素的相对次序未变，所以插入排序是稳定的)
}
}
int main()
{
int A[] = { 6, 5, 3, 1, 8, 7, 2, 4 };// 从小到大插入排序
int n = sizeof(A) / sizeof(int);
InsertionSort(A, n);
printf("插入排序结果：");
for (int i = 0; i < n; i++)
{
}
printf("%d ", A[i]);
printf("\n");
return 0;
}
2. 希尔排序（Shells Sort）
public class ShellSort {
/**
* 希尔排序的一趟插入
* @param arr 待排数组
* @param d 增量
*/
public static void shellInsert(int[] arr, int d) {
for(int i=d; i=0 && arr[j]>temp) { //从后向前，找到比其小的数的位置
arr[j+d] = arr[j];
//向后挪动
j -= d;
}
if (j != i - d)
//存在比其小的数
arr[j+d] = temp;
}
}
public static void shellSort(int[] arr) {
if(arr == null || arr.length == 0)
return ;
int d = arr.length / 2;
while(d >= 1) {
shellInsert(arr, d);
d /= 2;
}
}
}
3. 直接选择排序（Straight Selection Sort）
工作原理：
每一次从待排序的数据元素中选出最小（或最大）的一个元素，存
放在序列的起始位置，直到全部待排序的数据元素排完。
稳定性：
选择排序是不稳定的排序方法（比如序列[5， 5， 3]第一次就将第
一个[5]与[3]交换，导致第一个 5 挪动到第二个 5 后面）。
时间复杂度：
比较次数 O(n^2），比较次数与关键字的初始状态无关，总的比较
次数 N=(n-1）+(n-2）+...+1=n*(n-1）/2。
交换次数 O(n），最好情况是，已经有序，交换 0 次；最坏情况下，
即待排序记录初始状态是按第一条记录最大，之后的记录从小到大顺序
排列，则需要移动记录的次数最多为 3（n-1），逆序交换 n/2 次。
空间复杂度：
O(1)。简单选择排序需要占用一个临时空间，在交换数值时使用。
比较：
与插入排序比较：直接选择排序和直接插入排序类似，都将数据分
为有序区和无序区，所不同的是直接播放排序是将无序区的第一个元素
直接插入到有序区以形成一个更大的有序区，而直接选择排序是从无序
区选一个最小的元素直接放到有序区的最后。选择排序是固定位置，找
元素。相比于插入排序的固定元素找位置，是两种思维方式。
与冒泡排序比较：冒泡算法最费时的一是两两比较，二是两两交换，
选择排序中交换次数比冒泡排序少多了，n 值较小时，选择排序比冒泡
排序快。
示例
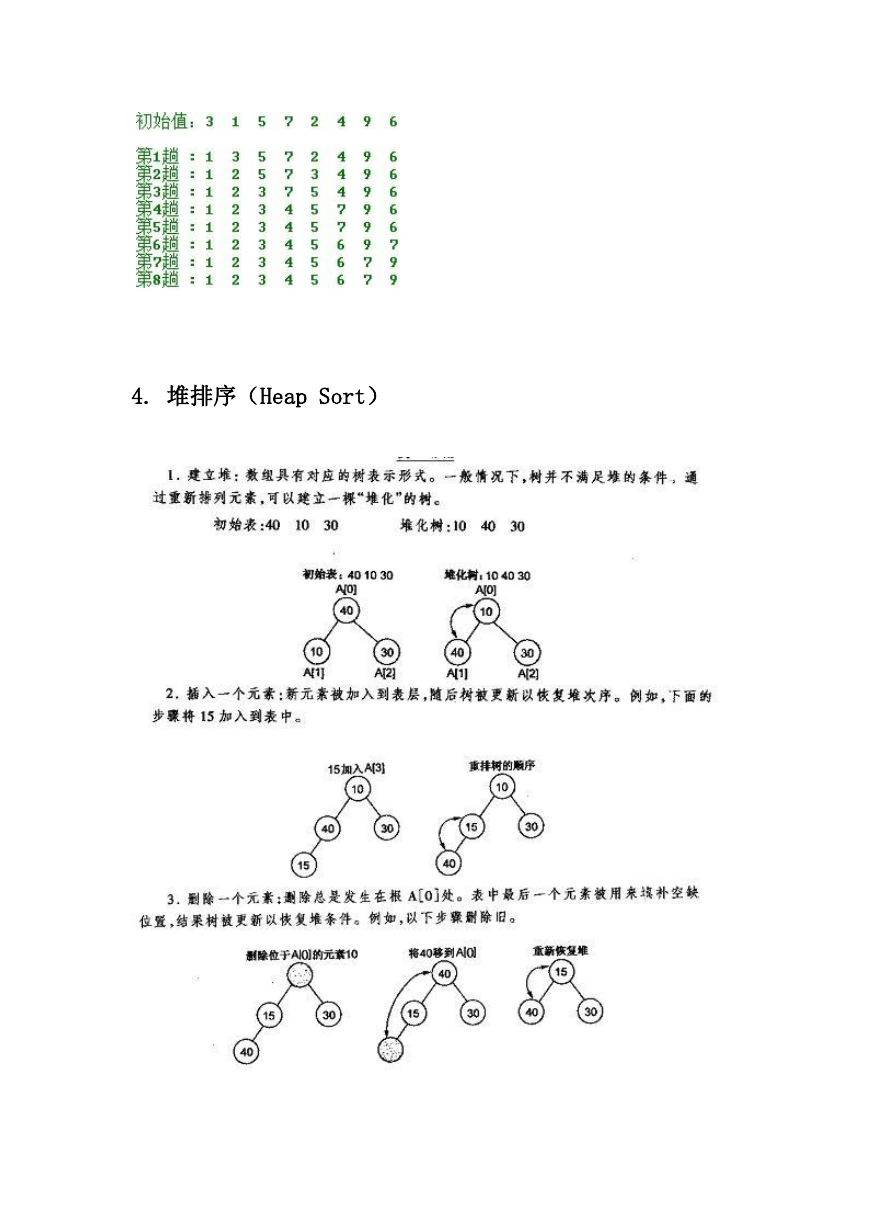
4. 堆排序（Heap Sort）
堆的插入
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点
到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这
个有序数据中——这就类似于直接插入排序中将一个数据并入到有序
区间中，不难写出插入一个新数据时堆的调整代码：
temp = a[i];
j = (i - 1) / 2;
while (j >= 0 && i != 0)
{
1. // 新加入 i 结点 其父结点为(i - 1) / 2
2. void MinHeapFixup(int a[], int i)
3. {
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18. }
a[i] = a[j];
i = j;
j = (i - 1) / 2;
if (a[j] <= temp)
break;
int j, temp;
}
a[i] = temp;
//父结点
//父节点以及插入节点限制
//把较大的子结点往下移动,替换它的子结点
//依次向上调整
更简短的表达为：
19. void MinHeapFixup(int a[], int i)
20. {
21.
for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (
i - 1) / 2)
Swap(a[i], a[j]);
22.
23. }
24.
插入时：
n 为最后的插入位置
1. //在最小堆中加入新的数据 nNum
2. void MinHeapAddNumber(int a[], int n, int nNum)
3. {
4.
5.
6. }
a[n] = nNum;
MinHeapFixup(a, n);
堆的删除
按定义，堆中每次都只能删除第 0 个数据。为了便于重建堆，实际的操
作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从
上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这
个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考
虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代
码：
1. // 从 i 节点开始调整,n 为节点总数 从 0 开始计算 i 节点的子节点
为 2*i+1, 2*i+2
int j, temp;
temp = a[i];
j = 2 * i + 1;
while (j < n)
{
2. void MinHeapFixdown(int a[], int i, int n)
3. {
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21. }
a[i] = a[j];
i = j;
j = 2 * i + 1;
}
a[i] = temp;
//把较小的子结点往上移动,替换它的父结点
if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
j++;
if (a[j] >= temp)
break;
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
