The exercises of Chapter Three 3.2 Given the grammar A→AA|(A)|ε a. b. Describe the language it generates; Show that it is ambiguous. [Solution]: a. Generates a string of balanced parenthesis, including the empty string. b. parse trees of (): A A ε ) ( ( 3.3 Given the grammar A A ) ε A A ε term exp  exp addop term | addop  + | - term term mulop factor| factor mulop  * factor ( exp ) | number expression: [Solution]: Write down leftmost derivations, parse trees, and abstract syntax trees for the following a. 3+4*5-6 b. 3*(4-5+6) c. 3-(4+5*6) a. The leftmost derivations for the expression 3+4*5-6: Exp => exp addop term =>exp addop term addop term =>term addop term addop term=> factor addop term addop term =>3 addop term addop term => 3 + term addop term =>3+term mulop factor addop term =>3+factor mulop factor addop term =>3+4 mulop factor addop term => 3+4* factor addop term 

=>3+4*5 addop term => 3+4*5-term=> 3+4*5-factor=>3+4*5-6 3.5 Write a grammar for Boolean expressions that includes the constants true and false, the operators and, or and not, and parentheses. Be sure to give or a lower precedence than and and and a lower precedence that not and to allow repeated not’s, as in the Boolean expression not not true. Also be sre your grammar is not ambiguous. [solution] bexp→bexp or A | A A→ A and B | B B→ not B | C C→ (bexp) | true | false Ex: not not true boolExp → A → B → not B → not not B → not not C → not not true 3.8 Given the following grammar statement→if-stmt | other | ε if-stmt→ if ( exp ) statement else-part else-part→ else statement | ε 

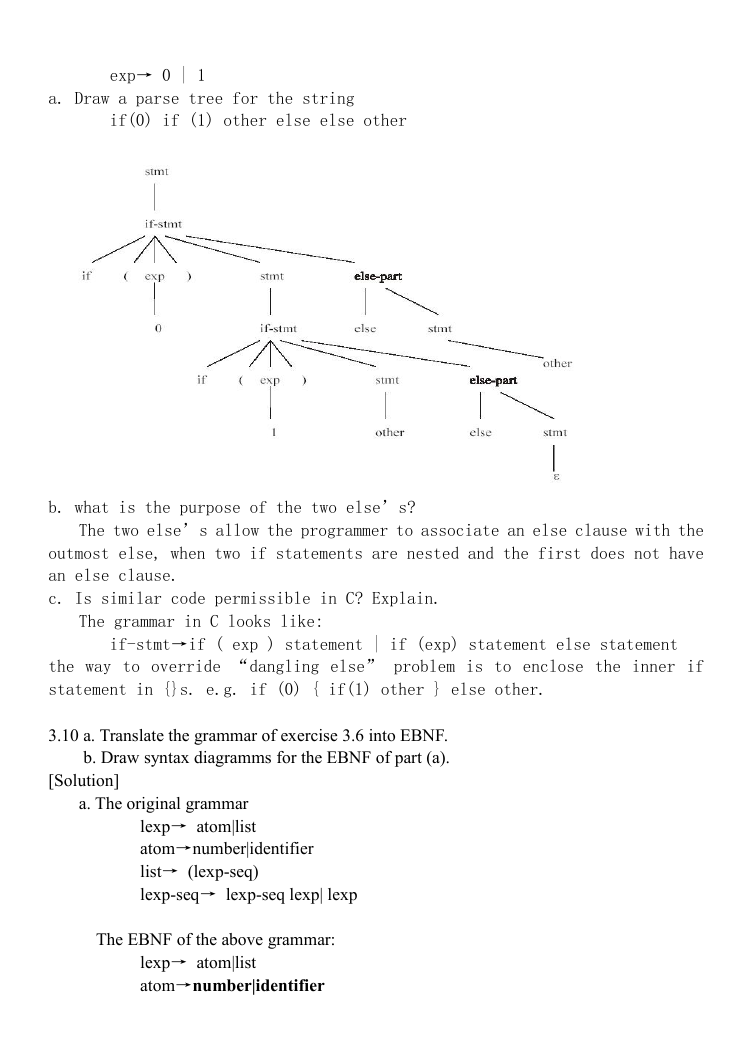
exp→ 0 | 1 a. Draw a parse tree for the string if(0) if (1) other else else other b. what is the purpose of the two else’s? The two else’s allow the programmer to associate an else clause with the outmost else, when two if statements are nested and the first does not have an else clause. c. Is similar code permissible in C? Explain. The grammar in C looks like: if-stmt→if ( exp ) statement | if (exp) statement else statement the way to override “dangling else” problem is to enclose the inner if statement in {}s. e.g. if (0) { if(1) other } else other. 3.10 a. Translate the grammar of exercise 3.6 into EBNF. 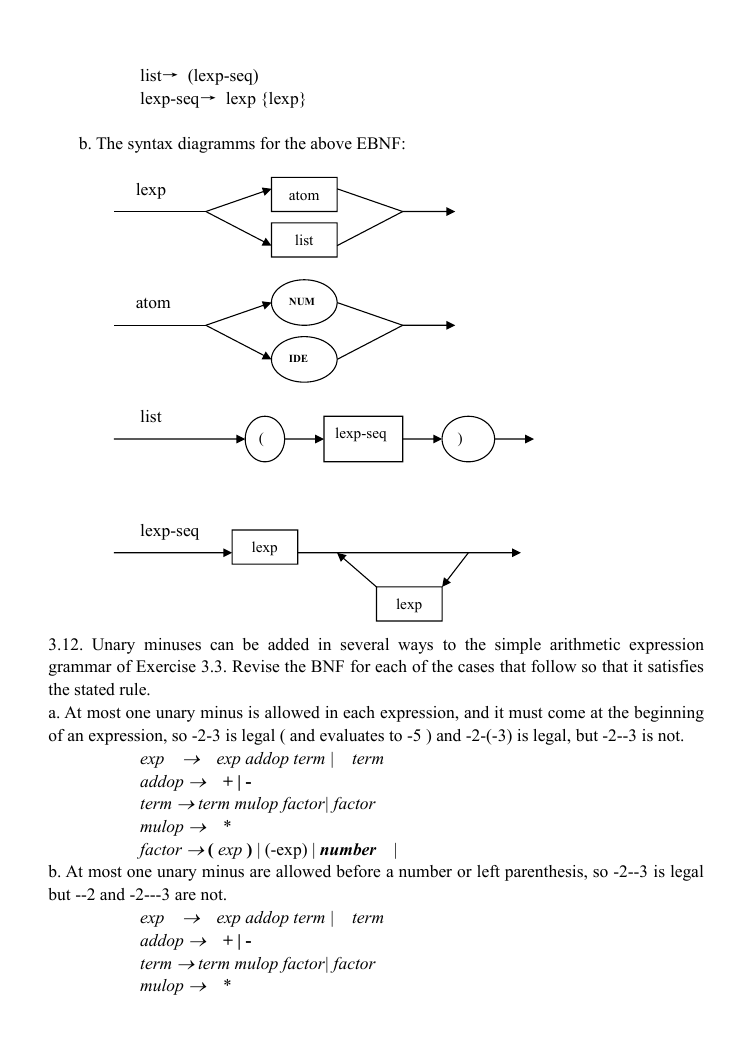b. Draw syntax diagramms for the EBNF of part (a). [Solution] a. The original grammar lexp→ atom|list atom→number|identifier list→ (lexp-seq) lexp-seq→ lexp-seq lexp| lexp The EBNF of the above grammar: lexp→ atom|list atom→number|identifier 

list→ (lexp-seq) lexp-seq→ lexp {lexp} b. The syntax diagramms for the above EBNF: lexp atom list atom list NUM IDE ( lexp-seq ) lexp-seq lexp lexp 3.12. Unary minuses can be added in several ways to the simple arithmetic expression grammar of Exercise 3.3. Revise the BNF for each of the cases that follow so that it satisfies the stated rule. a. At most one unary minus is allowed in each expression, and it must come at the beginning of an expression, so -2-3 is legal ( and evaluates to -5 ) and -2-(-3) is legal, but -2--3 is not. term exp  exp addop term | addop  + | - term term mulop factor| factor mulop  * factor ( exp ) | (-exp) | number b. At most one unary minus are allowed before a number or left parenthesis, so -2--3 is legal but --2 and -2---3 are not. | exp  exp addop term | addop  + | - term term mulop factor| factor mulop  * term 

factor ( exp ) | -(exp) | number | -number c. Arbitrarily many unary minuses are allowed before numbers and left parentheses, so everything above is legal. 3.19 In some languages ( Modula-2 and Ada are examples), a procedure declaration is expected to be terminated by syntax that includes the name of the procedure. For example, in Modular-2 a procedure is declared as follows: PROCEDURE P; BEGIN …… END P; Note the use of the procedure name P alter the closing END. Can such a requirement be checked by a parser? Explain. [Answer] This requirement can not be handled as part of the grammar without making a new rule for each legal variable name, which makes it intractable for all practical purposes, even if variable names are restricted to a very short length. The parser will just check the structure, that an identifier follows the keyword PROCEDURE and an identifier also follows the keyword END, however checking that it is the same identifier is left for semantic analysis. See the discussion on pages 131-132 of your text. 3.20 a. Write a regular expression that generate the same language as the following grammar: A→ aA|B|ε B→ bB|A b. Write a grammar that generates the same language as the following regular [Solution] expression: (a|c|ba|bc)*(b|ε) a. The regular expression: (a|b)* b. The grammar: Step 1: A→ BC B→aB|cB|baB|bcB|ε C→b|ε A→ Bb|B B→aB|cB|baB|bcB|ε Step 2: