脉冲神经元模型—SRM模型.pdf-资料库

baidu_29900531-10694193-4744302543009332143.pdf-第1页.png

第1页 / 共53页

baidu_29900531-10694193-4744302543009332143.pdf-第2页.png

第2页 / 共53页

baidu_29900531-10694193-4744302543009332143.pdf-第3页.png

第3页 / 共53页

baidu_29900531-10694193-4744302543009332143.pdf-第4页.png

第4页 / 共53页

baidu_29900531-10694193-4744302543009332143.pdf-第5页.png

第5页 / 共53页

baidu_29900531-10694193-4744302543009332143.pdf-第6页.png

第6页 / 共53页

baidu_29900531-10694193-4744302543009332143.pdf-第7页.png

第7页 / 共53页

baidu_29900531-10694193-4744302543009332143.pdf-第8页.png

第8页 / 共53页

Thisispage Printer:Opaquethis TheSpikeResponseModel WulframGerstner

Thisispage Printer:Opaquethis MNN September ,

.TheSpikeResponseModel ABSTRACTAdescriptionofneuronalactivityonthelevelofionchannels, asintheHodgkin-Huxleymodel,leadstoasetofcouplednonlineardier- entialequationswhicharediculttoanalyze.Inthispaper,wepresenta conceptualframeworkforareductionofthenonlinearspikedynamicsto athresholdprocess.Spikesoccurifthemembranepotentialu(t)reachesa threshold#.Thevoltageresponsetospikeinputisdescribedbythepostsy- napticpotential.Postsynapticpotentialsofseveralinputspikesareadded linearlyuntilureaches#.Theoutputpulseitselfandthereset/refractory periodwhichfollowthepulsearedescribedbyafunction.Sinceand canbeinterpretedasresponsekernels,theresultingmodeliscalledthe SpikeResponseModel(SRM).AfterashortreviewoftheHodgkin-Huxley modelweshowthat(i)Hodgkin-Huxleydynamicswithtime-dependent inputcanbereproducedtoahighdegreeofaccuracybytheSRM;(ii) thesimpleintegrate-and-reneuronisaspecialcaseoftheSpikeResponse Model;(iii)compartmentalneuronswithapassivedendritictreeanda thresholdprocessforspikegenerationcanbetreatedinSRM-framework; (iv)smallnonlinearitiesleadtointeractionsbetweenspikestobedescribed byhigher-orderkernels. Introduction Thesuccessfulmathematicaldescriptionofactionpotentialsinthegiant axonofthesquidbyHodgkinandHuxleyin hasleadtoawhole seriesofmodelingpaperswhichtrytodescribeindetailthedynamicsof variousionchannelsonthesomaanddendritesduringspikereceptionand spikeemission.Withmoderncomputersitisnowpossibletonumerically integratemodelswithtotypesofionchannelandhundredsofspa- tialcompartments[YKA ,TWMM ,BB ]andreproduceexperimental ndingstoahighdegreeofaccuracy.Ontheotherhand,itisoftendi- culttograspintuitivelytheessentialphenomenaofneuronaldynamicsfrom thesemodels.Inparticular,itisoutofreachtounderstandthesemodels analytically.Moreover,inanetworksettingthequestionariseswhetherall thedetailsdescribedincompartmentalmodelsarenecessarytounderstand thecomputationinlargepopulationsofneurons. Forananalyticalunderstandingofnetworksofspikingneurons,asimpli- eddescriptionofneuronaldynamicsisthereforedesirable[AK ,Abb ]. Forthisreasonintegrate-and-remodels[Lap,Ste,Tuc]havebe- comeincreasinglypopularfortheinvestigationofprinciplesofcortical dynamicsandfunction,e.g.,[MS ,AvV ,Tre ,SNS ,BH ].The reductionofdetailedneuronmodelstoastandardintegrate-and-reunit requiressimplicationsinatleasttworespects.First,thenonlineardynam- icsofspikegeneration[HH,RE ]mustbereducedtoaleakyintegrator withthresholdring[AK ].Second,eectsofthespatialstructureofthe neuron[Ral,Tuc,AFG ,BT ]mustbereducedtosomeeective input[Abb ].

.TheSpikeResponseModel Inthispaperweaddressbothissuesfromthesystematicpointofviewofa responsekernelexpansion.ItisshownthatspikegenerationintheHodgkin- Huxleymodelcanbereproducedtoahighdegreeofaccuracybyasingle- variablethresholdmodel[KGvH ].Theproblemofspatialstructureis studiedforamulti-compartmentalintegrate-and-remodelwithapassive dendritictree[AFG ,BT ]andactivecurrentsatthesoma.Inthiscase, themodeldynamicscanbesolvedandsystematicallyreducedtoasingle- variablemodelwithresponsekernels. Afterthereductionoftheintricateneuronaldynamicstoathreshold model,itisthenpossibletostudyanalyticallythedynamicsofnetworks ofneurons.Ithasbeenshownpreviouslythatinalargenetworkofmodel neuronswithhomogeneouscouplings,thestabilityofcoherent,incoherent, orpartiallycoherentstatescanbeunderstoodinatransparentmanner [AvV ,GvH ,Ger ,GvHC ,BH ].Moreover,thecollectiveresponse ofapopulationofspikingneuronstoacommontime-dependentinputcan beanalyzed[Ger].Themathematicalconsiderationsthatarenecessary forareductionofthehighlynonlinearHodgkin-Huxleyequationstoa single-variablethresholdmodelarethereforeworththeeort. Thechapterisorganizedasfollows.Westartinsectionwithareview ofthestandardHodkgin-Huxleymodel.Thefourdierentialequationsof HodgkinandHuxleygiveanaccuratedescriptionofneuronalspikinginthe giantaxonofthesquid.Thedrawbackisthattheyarehighlynon-linear andthereforediculttoanalyzemathematically.Wethereforeaimfora simplerphenomenologicaldescription.Themethodweproposeisbasedon spikeresponsekernelsandprovidesabiologicallytransparentdescription oftheessentialeectsduringspiking.Inthesecondpartofsection,we willseethattheSpikeResponseModel(SRM),derivedfromtheHodgkin- HuxleymodelbytheSpikeResponseMethod,canreproduceupto percentofthespiketimesoftheHodkgin-Huxleymodelcorrectly. AshortsummaryofthemathematicsoftheSpikeResponseModelis presentedinsection.Anotherwell-knownmodelofneuronalspikingisthe integrate-and-remodelwhichisreviewedinsection.Weshowthatthe integrate-and-reisinfactofspecialcaseoftheSpikeResponseModel.The mappingfromtheintegrate-and-remodeltotheSpikeResponseModelis discussedinsomedetailinsections..and..Insectionweaddressthe questionofspatialstructure.Weshowthatinthecaseofalineardendritic treethedynamicscanbewellcapturedbyspikeresponsekernels.Finally insectionwediscussweaklynon-lineareects.Throughoutthetext,the generalargumentsareinteruptedbyexamplesintendedtoillustratethe mainresults.

- + C R K I Na - + + - + Na outside K Cl inside - .TheSpikeResponseModel FIGURE.SchematicdiagramfortheHodgkin-Huxleymodel.Takenfrom [Ger ]. Hodgkin-Huxleymodel TheclassicdescriptionofneuronalspikingdatesbacktoHodgkinand Huxley[HH]whosummarizedtheirextensiveexperimentalstudieson thegiantaxonofthesquidwithfourdierentialequations.Arstand fundamentalequationdescribestheconservationofelectriccurrents.Then therearethreefurtherdierentialequationswhichdescribethedynamicsof sodiumandpotassiumionchannels.Modernmodelsofneuronaldynamics makeuseofthesametypeofequations,butofteninvolvemanymore dierentionchanneltypes.Theionchannelsmaybelocatedondierent compartmentsofaspatiallyextendedneuronmodel.Asingleneuronmay thenbedescribedbyhundredsofcouplednon-lineardierentialequations. InthissectionwesticktothestandardHodgkin-Huxleymodelwithout spatialstructureanduseitasareferencemodeltostudythedynamics ofspikegeneration.IntherstsubsectionwereviewtheHodgkin-Huxley equations.Inthesecondsubsectionwereducethenonlineardynamicsof theHodgkin-Huxleymodeltoathresholdmodelwithasinglevariable u(t).ThisreductionwillbethebasisforadiscussionoftheSpikeResponse ModelinSections-. .Denitionofthemodel TheHodgkin-HuxleymodelcanbeunderstoodwiththehelpofFig.. Thesemipermeablecellmembraneseparatestheinteriorofthecellfrom theextracellularliquid.Duetothemembrane'sselectivepermeabilityand alsobecauseofactiveiontransportthroughthecellmembrane,theion concentrationinsidethecellisdierentfromtheoneintheextracellular liquid.Thedierenceinconcentrationgeneratesanelectricalpotentialbe- tweentheinteriorandtheexteriorofthecell.Thecellmembraneactslike acapacitorwhichhasbeenchargedbyabattery.IfaninputcurrentI(t) isinjectedintothecell,itmayaddfurtherchargeonthecapacitor,orleak throughthechannelsinthecellmembrane.

1.0 m n -50.0 10.0 5.0 h m -50.0 0.0 50.0 100.0 50.0 100.0 h n 0.0 u [mV] ) u ( 0 x 0.5 ] s m [ ) u ( τ u [mV] 0.0 -100.0 0.0 -100.0 .TheSpikeResponseModel a) b) FIGURE.Equilibriumfunction(a)andtimeconstant(b)forthethreevari- ablesm;n;hintheHodgkin-Huxleymodel.Takenfrom[Ger ]. Letusnowtranslatetheaboveconsiderationsintomathematicalequa- tions.Theconservationofelectricchargeonapieceofmembraneimplies thattheappliedcurrentI(t)maybesplitinacapacitivecurrentICwhich chargesthecapacitorCandfurthercomponentsIkwhichdiusethrough theionchannels.Thus I(t)=IC+XkIk (.) wherethesumrunsoverallionchannels.InthestandardHodgkin-Huxley modelthereareonlythreetypesofchannel:asodiumchannelwithindex Na,apotassiumchannelwithindexKandanunspecicleakagechannel withresistanceR;cf.Fig..FromthedenitionofacapacityC=Q=u whereQisachargeanduthevoltageacrossthecapacitor,wendthe chargingcurrentIC=Cdu=dt.Hencefrom(.) Cdudt=XkIk+I(t): (.) Inbiologicalterms,uisthevoltageacrossthemembraneandPkIkisthe sumoftheioniccurrentswhichpassthroughthecellmembrane. Asmentionedabove,theHodgkin-Huxleydescribesthreetypesofchan- nel.Allchannelsmaybecharacterizedbytheirresistanceor,equivalently, bytheconductance.Theleakagechannelisdescribedbyavoltage-inde- pendentconductancegL==R;theconductanceoftheotherionchannels isvoltagedependent.Ifthechannelsarefullyopen,theytransmitcurrents withamaximumconductancegNaorgK,respectively.Normally,however, thechannelsarepartiallyblocked.Theremovaloftheblockisvoltagede- pendentandisdescribedbyadditionalvariablesm;n,andh.Thecombined actionofmandhcontrolstheNachannels.TheKgatesarecontrolledbyn. Specically,HodgkinandHuxleyformulatedthethreecurrentcomponents as XkIk=gNamh(uVNa)+gKn(uVK)+gL(uVL): (.) TheparametersVNa,VK,andVLarecalledreversalpotentialssincethe

.TheSpikeResponseModel x ux gx mV mS/cm Na mS/cm K -mV .mV .mS/cm L x x(u=mV) x(u=mV) (::u)=[exp(:u)] n :exp(u=) m(::u)=[exp(::u)] exp(u=) :exp(u=) h =[exp(:u)+] TABLE..TheparametersoftheHodgkin-Huxleyequations.Themembrane capacityisC=F/cm. directionofacurrentIkchangeswhenucrossesVk.Reversalpotentials andconductancesareempiricalparametersandsummarizedintable. Thethreevariablesm,n,andhevolveaccordingtothedierentialequa- tions _m=m(u)(m)m(u)m _n=n(u)(n)n(u)n _h=h(u)(h)h(u)h (.) with_m=dm=dt,andsoon.Theand,givenintable,areempirical functionsofuthathavebeenadjustedbyHodgkinandHuxleytotthe dataofthegiantaxonofthesquid.Eqs.(.)-(.)denetheHodgkin- Huxleymodel. Eachofthethreeequations(.)mayalsobewrittenintheform _x=x(u)[xx(u)] (.) wherexstandsform,n,orh.Forxedvoltageu,thevariablexap- proachesthevaluex(u)withatimeconstantx(u).Theasymptoticvalue x(u)andthetimeconstantx(u)aregivenbythetransformationx(u)= x(u)=[x(u)+x(u)]andx(u)=[x(u)+x(u)].Usingtheparame- tersgivenbyHodgkinandHuxley[HH],wehaveplottedinFig.the functionsx(u)andx(u). ..Example:Spikegeneration WeseefromFig.athatmandnincreasewithuwhereashdecreases. Thus,ifsomeexternalinputcausesthemembranevoltagetorise,theion conductanceofsodium(Na)increasesduetoincreasingmandpositive sodiumionsowintothecell.Thisraisesthemembranepotentialeven further.Ifthispositivefeedbackislargeenough,anactionpotentialis initiated.

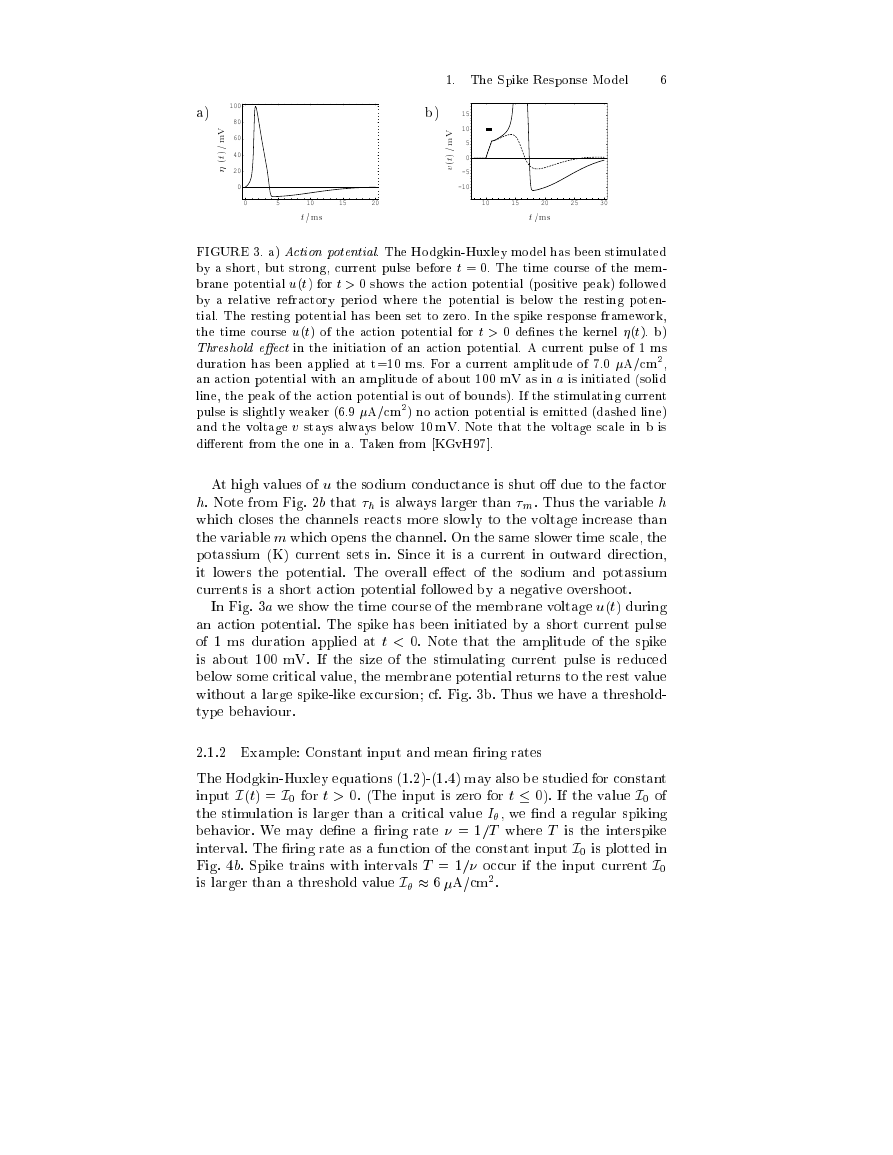
V m = ) t ( U 5 10 15 20 0 20 25 30 -5 80 60 40 20 0 15 10 5 0 15 10 100 -10 V m = ) t ( .TheSpikeResponseModel a) b) t=msv t=ms FIGURE.a)Actionpotential.TheHodgkin-Huxleymodelhasbeenstimulated byashort,butstrong,currentpulsebeforet=.Thetimecourseofthemem- branepotentialu(t)fort>showstheactionpotential(positivepeak)followed byarelativerefractoryperiodwherethepotentialisbelowtherestingpoten- tial.Therestingpotentialhasbeensettozero.Inthespikeresponseframework, thetimecourseu(t)oftheactionpotentialfort>denesthekernel(t).b) Thresholdeectintheinitiationofanactionpotential.Acurrentpulseofms durationhasbeenappliedatt=ms.Foracurrentamplitudeof.A/cm, anactionpotentialwithanamplitudeofaboutmVasinaisinitiated(solid line,thepeakoftheactionpotentialisoutofbounds).Ifthestimulatingcurrent pulseisslightlyweaker(. A/cm)noactionpotentialisemitted(dashedline) andthevoltagevstaysalwaysbelowmV.Notethatthevoltagescaleinbis dierentfromtheoneina.Takenfrom[KGvH ]. Athighvaluesofuthesodiumconductanceisshutoduetothefactor h.NotefromFig.bthathisalwayslargerthanm.Thusthevariableh whichclosesthechannelsreactsmoreslowlytothevoltageincreasethan thevariablemwhichopensthechannel.Onthesameslowertimescale,the potassium(K)currentsetsin.Sinceitisacurrentinoutwarddirection, itlowersthepotential.Theoveralleectofthesodiumandpotassium currentsisashortactionpotentialfollowedbyanegativeovershoot. InFig.aweshowthetimecourseofthemembranevoltageu(t)during anactionpotential.Thespikehasbeeninitiatedbyashortcurrentpulse ofmsdurationappliedatt<.Notethattheamplitudeofthespike isaboutmV.Ifthesizeofthestimulatingcurrentpulseisreduced belowsomecriticalvalue,themembranepotentialreturnstotherestvalue withoutalargespike-likeexcursion;cf.Fig.b.Thuswehaveathreshold- typebehaviour. ..Example:Constantinputandmeanringrates TheHodgkin-Huxleyequations(.)-(.)mayalsobestudiedforconstant inputI(t)=Ifort>.(Theinputiszerofort).IfthevalueIof thestimulationislargerthanacriticalvalueI,wendaregularspiking behavior.Wemaydenearingrate==TwhereTistheinterspike interval.TheringrateasafunctionoftheconstantinputIisplottedin Fig.b.SpiketrainswithintervalsT==occuriftheinputcurrentI islargerthanathresholdvalueIA/cm.

资料库

脉冲神经元模型—SRM模型.pdf

相关推荐

人工智能

热门标签

最新资料