论文研究-列车间多频段直接通信系统设计及性能分析.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：1.68M 资料格式：pdf 举报版权申诉

weixin_38743481-11691811-16359647345464381748.pdf-第1页.png

第1页 / 共9页

weixin_38743481-11691811-16359647345464381748.pdf-第2页.png

第2页 / 共9页

weixin_38743481-11691811-16359647345464381748.pdf-第3页.png

第3页 / 共9页

weixin_38743481-11691811-16359647345464381748.pdf-第4页.png

第4页 / 共9页

weixin_38743481-11691811-16359647345464381748.pdf-第5页.png

第5页 / 共9页

weixin_38743481-11691811-16359647345464381748.pdf-第6页.png

第6页 / 共9页

weixin_38743481-11691811-16359647345464381748.pdf-第7页.png

第7页 / 共9页

weixin_38743481-11691811-16359647345464381748.pdf-第8页.png

第8页 / 共9页

文本预览

104 2017，53（13） Computer Engineering and Applications 计算机工程与应用 ⦾网络、通信与安全⦾ 列车间多频段直接通信系统设计及性能分析李淑娟，李茂青，高云波，林俊亭，江娜 LI Shujuan, LI Maoqing, GAO Yunbo, LIN Junting, JIANG Na 兰州交通大学自动化与电气工程学院，兰州 730070 School of Automation & Electrical Engineering, Lanzhou Jiao Tong University, Lanzhou 730070, China LI Shujuan, LI Maoqing, GAO Yunbo, et al. Performance analysis of multiband direct communication between trains in tunnel. Computer Engineering and Applications, 2017, 53（13）：104-112. Abstract: It is most significant that train- to- train direct communication system can reduce the incidence of railway accidents effectively. However the direct communication system in plain environment has been proposed only. A new kind of multiband frequency receiver and transmitter that can be applied in both plain and tunnel environment are designed for direct communication system, then the communication performance in tunnel is analyzed. Firstly, the working frequency band and the communication distance of millimeter waves are decided for railway application requirements in tunnel. In the second place, the multiband frequency receiver and transmitter are proposed for both plain and tunnel envi- ronment, then the sensitivity of the designed receiver is computed. Moreover, the propagation mode of electromagnetic wave is analyzed in tunnel. Then the loss model of roughness and different form in tunnel is researched. The corresponding tent law and the multipath effect of propagating of electromagnetic wave are calculated. With all the above methods, the deterministic and statistic model of direct communication channel in single and double line railway tunnel are established. Meanwhile, the simulation results show the feasibility of the proposed 8 mm wave based direct communication scheme between trains. Key words: millimeter waves; working frequency band; tunnel; direct communication channel; deterministic model; sta- tistic model 摘要：列车间直接通信对减少铁路交通事故的发生具有重大意义，但是目前只设计出了平原环境下列车间直接通信的通信系统。设计了既适用于平原环境也适用于隧道环境下列车间直接通信的多频段通信系统下并在隧道环境下分析了该通信系统的通信性能。确定了适合隧道环境中通信的毫米波工作频段和通信范围；设计了既可适用于平原环境也可适用于隧道环境下的多频段接收机和多频段发射机，并计算了接收机的灵敏度；最后通过分析电磁波在隧道内的传播方式、隧道壁粗糙度以及不同隧道类型对电磁波的损耗模型、帐篷定律以及隧道环境下电磁波传播的多径效应，分别建立了单线和双线铁路隧道中列车间直接通信信道的确定性模型和统计模型。通过仿真分析得出，所提出的隧道中列车间 8 mm 波直接通信方案是可行的。关键词：毫米波；工作频段；隧道；直接通信信道；确定性模型；统计模型文献标志码：A 中图分类号：U285.21；TN929.5 doi：10.3778/j.issn.1002-8331.1601-0406 1 引言列车间直接通信是一种不依赖于地面设备，仅通过车载设备实现前后行列车间直接通信的技术。该系统能够使前后行列车实时交换彼此的速度、位置等信息，基金项目：国家自然科学基金地区项目（No.61164010）；甘肃省自然科学基金（No.1508RJZA058）。作者简介：李淑娟（1988—），女，硕士研究生，主要研究领域为铁路通信与信号技术，E-mail：lis_juan@126.com；李茂青（1973—），男，博士，副教授，主要研究领域为列车运行控制、铁路通信与信号技术。收稿日期：2016-01-29 修回日期：2016-04-05 文章编号：1002-8331（2017）13-0104-09 CNKI 网络优先出版：2016-05-19, http://www.cnki.net/kcms/detail/11.2127.TP.20160519.1541.004.html 计算机工程与应用www.ceaj.org

李淑娟，李茂青，高云波，等：列车间多频段直接通信系统设计及性能分析 2017，53（13） 105 提高列车运行的安全性，其发射机和接收机均安装在列车顶部随着列车高速移动[1]。然而在现有 GSM-R 铁路通信系统中，发射机是固定的，接收机是随着列车移动的。目前应用在隧道中的 GSM-R 系统是通过基站+光纤直放站+泄露电缆的方式进行网络覆盖从而实现列车间间接通信[2]，因此在分析隧道中列车间直接通信时不能完全按照 GSM-R 通信来分析。本文首先确定了适合隧道中列车间直接通信的工作频段和通信距离；然后通过研究平原环境下列车间直接通信系统的接收机和发射机[1]，结合 MIMO 系统的多输入多输出接收机和发射机，设计了一种能同时在平原环境和隧道环境中实现列车间直接通信的多频段接收机和多频段发射机；其次对隧道环境下电磁波的传播特性进行研究，给出无线电波在各类型隧道环境中的传播损耗模型，进而建立隧道环境下无线电波的信道模型，并分析其信道特性。 2 通信系统设计 2.1 工作频段保证高质量通信的首要工作就是选择合适的通信频率，现有的 GSM-R 通信系统的工作频率在 900 MHz 左右。本文将隧道视为有损介质波导，然而较低频段的电磁波在有损介质波导中传播效率很差，因此所选的工作频段在隧道中必须具有较大的传播优势[3]。本文所选的工作频段为毫米波频段，毫米波一般为 26.5~300 GHz 的电磁波，相应的波长为 1 cm~1 mm，毫米波频段进一步分为 Ka 频段（26.5~40 GHz），V 频段（40~75 GHz），W 频段（75~110 GHz），T 频段（110~180 GHz）等；同时也可以用大气传播窗口中心频率表示为 34 GHz、60 GHz、 94 GHz、140 GHz、220 GHz 频段；或者用相应的波长表示为 8 mm、5 mm、2 mm、1 mm 频段。毫米波段与超短波以及 GSM-R 的 900 MHz 工作频段相比较具有以下优点[4]：（1）毫米波具有波导效应可以在非常严峻的条件下很好的传播，在隧道中的传输衰减更小，在无中继的条件下传播距离更远；（2）毫米波波长短，天线增益高，可以降低发射功率，减小部件和系统的体积；（3）毫米波的频带宽，分辨率高，信息速率高，传输容量大，可以应用宽频谱抑制多径干扰和起伏，有极高的数据传输速率和调频能力；（4）相对于超短波和微波而言，毫米波具有定向性，在传播的过程中波束比较集中，干扰少，可以提供更加稳定可靠的通信。综上所述，对于隧道这种有损介质波导而言，本文选择毫米波实现列车间的直接通信。毫米波一般用于短程通信，短程通信可以分为两类：一类是大气窗口的 8 mm 通信，主要降低大气衰减；另一类是吸收峰值 60 GHz 通信，主要用于军事保密通信。因此本文选择 8 mm 频段作为通信频段。 2.2 通信范围的确定 h1 + h2 ) 毫米波视距通信距离估算公式如下式所示： d = 3.57( 其中，h1、h2 可得视距通信距离 d = 16 km 。（1）为列车天线高度，一般取 h1 = h2 = 5.2 m [5]。电磁波在隧道内的传播区域可分为近场区和远场区，在近场区存在直射波，电磁波的传播特性与自由空间内相同；远场区不存在直射波，电磁波的传播与在波导中的传播相似。近场区与远场区的转折点通过 Fresnel 理论来确定[3]： d = maxæ èç h2 λ , w2 λ ö ø÷ （2）其中，h 为隧道的高，w 为隧道的宽，λ 为电磁波波长。就单线铁路隧道而言，隧道宽 4.46 m，高 5.87 m。等效为矩形隧道计算，带入本文中所确定的工作波长 8 mm 得到近场区和远场区的转折点为 4.3 km，为了通信的可靠性要求通信距离应大于最大紧急制动距离的两倍；该通信技术在平原环境下 15 km 的通信距离是在列车时速为 180 km/h，运行时间间隔为 5 min 的情况下确定的；然而《铁路隧道规范中》规定在隧道地区列车需要减速运行，此时旅客列车的时速等于或小于 160 km/h，货物列车的时速等于或小于 120 km/h，若此时列车运行间隔为 3 min，那么两通信列车同时在长大隧道（10 km 以上的隧道）内的通信距离旅客列车间的通信距离为8 km，货物列车间的通信距离为 6 km；又因为长大隧道中也存在弯曲隧道此时列车时速要更小，所以结合以上分析，长大隧道环境下的列车间直接通信的距离确定为 8 km。 2.3 多频段接收机应用于通信系统的接收机，应具备以下特点：较低的噪声系数（在甚高频或更高频下），较小的群时延变化和互调失真，较大的频率动态范围，稳定的自动增益控制，适当的射频增益和中频增益，极好的频率稳定度和频率平坦度，低相位噪声，低带内干扰，足够的可选择性和适当的误比特率等[7]。因此，在设计系统接收机时，应将这些因素均考虑在内。移动通信的飞速发展对无线接收机提出了更严格的要求，譬如，低功耗、高可靠性、低价格、小尺寸，以及具有适应不同通信环境和不同通信标准的灵活性等。这就要求所设计的无线通信接收机的灵活性更大，功能更多，能接收不同射频标准提供的信息。因此，本文所设计的接收机是一种灵活性大，多功能的多频段接收机。列车间直接通信系统对环境的要求很严格，不同环境中的工作频段各不相同，在平原环境中采用超短波频段电磁波，而在隧道环境中采用毫米波频段电磁波。本文所设计的多频段接收机如图 1 所计算机工程与应用www.ceaj.org

106 2017，53（13） Computer Engineering and Applications 计算机工程与应用示，该接收机既能适用于平原环境也能适用于隧道环境，从而提高了通信的可靠性和通信设备的利用率。如图 1 所示，该接收机采用频率综合器[8]与列车定位系统相结合的方式，根据通信环境的不同产生不同的本振信号，并将其提供给第一混频器，同时又经过 n 分频器给第二混频器提供本振信号。假设该接收机的射频信号的频率为 fRF ，最终输出的中频信号为 fIF ，第一中频信号的频率为 fIF1 ，第一本振信号的频率为 fLO1 ，第二本振信号的频率为 fLO2 ，分频器的分频比为 n ，则上述各频率满足以下关系式：（3） ) ) fRF ± fIF n + 1 fIF n + 1( n + 1( n + 1 fRF ± n fLO1 = n fLO2 = 1 fRF ± fIF fIF = fRF - fLO1 = 1 本文所设计的接收机为适用于超短波和毫米波的多频段通信接收机，对不同的通信频段，需选择相应的合适的本振信号。对于毫米波段的高频段射频信号而言，频率综合器的基准频率需设置为 fLO1( = n n + 1( fRF( + fIF ，其第一中频频率为 fIF( ) ) - n 1 n + 1 fIF ；而对于低频段的射频信号而 n + 1 fRF( 言，频率综合器的基准信号需设置为 fLO1( = ) n ) n + 1( - fIF ，其第一中频频率为 fIF( fRF( ) + n 1 n + 1 fIF 。 n + 1 fRF( 高频段 ) 高频段 ) 低频段 ) 低频段 = ) 低频段 = 高频段 ) 高频段低频段灵敏度和选择性是接收机最主要的性能指标。灵敏度通常是频率的函数，因此在不同的工作频段下，接收机的灵敏度不同，灵敏度的计算公式如下式所示[9]： S = -174 + NF + 10 lg B + KM （4）其中，NF 为接收机的噪声系数；B 为检波前的中频带宽；KM 为调制特性的函数，与调制类型有关。 VHF\UHF 波段接收机的典型噪声系数为 6~12 dB，采用 10 kHz~5 MHz 的中频带宽；毫米波段接收机典型噪声系数为 3~6 dB，中频带宽 3.5 GHz，本文取 KM = 9 ，噪声系数 NF = 6 ，带宽 B = 3.5 GHz，则在 8 mm 波段下接收机的灵敏度为－150 dB。 2.4 多频段发射机在通信系统中，如果发射机设计不合理，就会产生 RF 干扰，不仅会干扰其他无线电设备，还会干扰各种非射频电气设备。因此在设计发射机时必须考虑以下几个参数：谐波输出、寄生输出、宽带噪声和近距离噪声、频率和幅度稳定性、信号的最大功率和平均功率。发射机的主要作用是实现有用低频信号对高频载波的调制，将其变为在某一中心频率上具有一定带宽的，适合通过天线发射的电磁波[10]。文献[11]提出了一种用于汽车防撞雷达的多频段毫米波发射机。因此根据不同频段发射机的不同系统结构，本文所设计的发射机具有的超短波支路和毫米波支路两个支路对毫米波频段而言，其发射机的前端与普通发射机的射频部分相同，唯一不同的是其载波频率进入了毫米波段，如图 2 所示。其中，发射机前端采用正交调制方案对基带信号进行调制，超短波支路原理与文献[1]中的原理相同；毫米波支路采用 4 倍频器将基带信号进行 4 倍频后与频率综合器产生的本振信号相混频得到毫米波，频率综合器的原理与上文所提接收机中频率综合器的原理相同。 3 隧道环境下无线电波的传播特性及信道模型 3.1 隧道环境下无线电波的传播特性隧道环境无线通信的首要问题是研究无线电波的传播特性。隧道可以被视为一个巨大的波导，无线电波在隧道中传播既有自由空间的传播特点，又受到隧道有 LNA 多频段带通滤波器镜像抑制滤波器第一中频滤波器第二中频滤波器解调器 1/n n 分频器频率综合器图 1 通信系统接收机结构图基带 I 乘法器振荡器分相器加法器多频段带通滤波器基带 Q 乘法器调制器 X4 多频段天线多频段带通滤波器图 2 通信系统发射机结构图计算机工程与应用www.ceaj.org

李淑娟，李茂青，高云波，等：列车间多频段直接通信系统设计及性能分析 2017，53（13） 107 限空间的影响有其独特的传播特性。因此隧道环境下的衰落也由空间损耗和多径效应构成[12]。此外电磁波在隧道中传播还受到介电常数，隧道壁粗糙度以及极化方式的影响，高度大于宽度的隧道中垂直极化波的传输效果更好[13]。本文主要讨论单线铁路隧道且通信天线采用垂直极化天线，因此只考虑垂直极化波的衰减，其衰减常数为[14]： Lv = 4.343λ2dæ çç è 1 W 3 ξr1 - 1 + ξr2 H 3 ξr2 - 1 ö ÷÷ ø （5）其中，λ 为波长，d 为传播距离，ξr1、ξr2 为隧道壁的电容率，干燥隧道壁的电容率为 ξr1 = ξr2 = 5 ，潮湿隧道壁的电容率为 ξr1 = ξr2 = 10 。如图 3 所示，垂直极化衰减常数随着距离及电容率的增大而增加。 45 40 35 30 25 20 15 10 5 0 数常减衰 ξr1 = ξr2 = 5 ξr1 = ξr2 = 10 1 2 3 4 5 6 距离/km 7 8 9 10 图 3 不同电容率下衰减常数与距离的关系假设隧道壁粗糙度服从均值为 0，方差为 δ2 的高斯分布，电磁波入射到隧道壁的入射角为 θ ，波的模式为 (m,n) [15]，隧道高度为 H ，宽度为 W ，传输距离为 d ，由粗糙度引起的衰减系数为[16]： nmax Lroughness( n = 1 é 4 sin3θ1 1 êê 2W λ2 ë 4 sin3θ2 + 4 sin2θ2 Hλ Lroughness = 1 + 4 sin2θ1 Wλ mmax∑ M ∑ m = 1 + sin θ1 W 2 ö ÷ ø 4.343π2δ2d )m,n = 1 2H æ ç è λ2 + （6） æ ç è + sin θ2 H 2 ù ö úú ÷ ø û 隧道中电磁波总的衰减常数为： Lsun = L0 + Lroughness + Lv （7）其中，L0 为不考虑隧道壁粗糙度时的衰减常数。如图 4 所示，随着入射角度和距离的增加，由粗糙度引起的衰减常数逐渐增大。电磁波在隧道中传播时，在近场区和远场区的传播方式不同，电磁波在近场区的传播与在自由空间中的传播特性相似，由于电磁波在自由空间中传播时以直射波的传播方式为主，不受障碍物的影响即不发生反射、散射及折射等现象，在近场区由于传播距离比较近，电磁波在传播过程中也不受障碍物的影响而发生反射、散射及折射等现象，以直射路径传播为主。因此普遍认为电 θ1 = θ2 = 30° θ1 = θ2 = 45° θ1 = θ2 = 60° θ1 = θ2 = 90° 15 10 5 数常减衰 0 1 2 3 4 5 6 距离/km 7 8 9 10 图 4 不同入射角下粗糙度衰减常数与距离的关系 PL = 20 lg f + 20 lg d + 32.44 磁波在近场区传播方式，类似于自由空间的传播方式故可以用自由空间的损耗模型进行分析，如式（8）所示[17]：（8）其中，f 为信号频率，d 为发射机和接收机之间的距离。由图 5 可看出，两列车间的追踪距离在近区范围内时，如果传输距离不变，电磁波的传播损耗随着频率增高而增大；如果工作频率不变，传播距离越大衰减越大。－100 －110 －120 －130 －140 －150 －160 －170 B d / 耗损输传 34 Ghz 60 Ghz 94 Ghz 1 2 3 4 5 6 距离/km 7 8 9 10 图 5 隧道中近区损耗与频率的关系图 5 表示毫米波的三个窗口值频率在同一隧道中的传输情况，从图中可以看出，频率越大随着距离的增加，传输衰减也越大，仿真结果与本文所选 34 GHz 电磁波的理论相一致。在远场区时，高次模的谐波被衰落殆尽，电磁波以主模进行传播，这种传播与电磁波在波导中的传播相似，ITU-R 给出的电磁波在远场区的损耗模型为： PL = 20 lg f + n lg d - A （9）其中，f 为信号频率，d 为发射机和接收机之间的距离，n 为距离因子，A 为常数项；距离因子 n 常数项 A 均与传播环境有关。由于隧道的长短不同，弯曲程度不同，因此电磁波在不同隧道环境中的传输特性也不同。根据近场区和远场区的损耗模型，结合测试数据得到四种不同隧道环境中电波传播的损耗模型如下[18]：（1）短直隧道中电磁波的传播损耗模型 PL = 20 lg f + 14.04 lg d + 32.89 （10）计算机工程与应用www.ceaj.org

108 2017，53（13） Computer Engineering and Applications 计算机工程与应用（11）（12）（2）长直隧道中电磁波的传播损耗模型 PL = 20 lg f + 20.28 lg d - 28.48 （3）弯曲短隧道中电磁波传播损耗模型 PL = 20 lg f + 5.54 lg d + 31.54 （4）弯曲长隧道中电磁波的传播损耗模型 PL = 20 lg f + 20.97 lg d - 28.02 （13）由图 6 和图 7 可得，电磁波在直隧道中的传播损耗要小于电磁波在弯曲隧道中的传播损耗，电磁波在短隧道中的传播损耗小于电磁波在长隧道中的传播损耗；根据所计算的毫米波段接收机的灵敏度（－150 dB），可得无论在哪一种类型的隧道中，也无论受何种因素的影响，通信距离 4 km 都能达到。 B d / 耗损输传 B d / 耗损输传 0 －20 －40 －60 －80 －100 －120 －140 短直隧道弯曲短隧道 1 2 3 4 5 6 距离/km 7 8 9 10 图 6 同一电磁波在短隧道中的传输情况 0 －20 －40 －60 －80 －100 －120 －140 长直隧道弯曲长隧道 1 2 3 4 5 6 距离/km 7 8 9 10 图 7 同一电磁波在长隧道中的传输情况 3.2 隧道环境中列车间直接通信信道的确定型模型在隧道环境下，从发射机发出的诸多电磁波到达接收机的射线条数遵循帐篷定律，根据帐篷定律的推论可以得到能被接收机接收到的射线条数如式（14）所示[19]：（14）其中，k = n + m ，n 和 m 分别为水平面反射次数和垂直面反射次数，C 由各种损耗及接收机灵敏度确定。 N = 2k2 + 2k + 1 ，0 ≤ k ≤ C 因此，可以根据帐篷定律建立隧道中列车间直接通信的信道模型。 3.2.1 多普勒频移速度差，最终会造成接收信号的频率发生波动而出现偏差，造成多普勒频移。多普勒频移会造成轻微的随机频率调制，与通信设备之间的相对运动速度密切相关，多普勒频移的计算如式（15）所示[20]： fd,n = fm cos αn = v c fc cos αn （15）其中，fd,n 表示第 n 条路径上信号的多普勒频偏，fm 表示最大多普勒频偏，fc 为载波，v 为通信设备的相对速度，α 为入射角。本文中，在无线通信的信道与两列车在平原环境下进行无线通信的信道相同，都是 M2M 信道，因此 M2M 信道的信号所服从的复包络的时间相关函数如式（16）和式（17）所示[21]： Rv(Δt) = σ2J0(2π λ V2Δt) Rv(Δt) = σ2J0(2πfMRΔt)J0(2πfMTΔt) （17）其中，J0 表示一类贝塞尔函数，fMR 为发射机的多普勒频偏极值，fMT 为接收机的多普勒频偏极值，V1 、V2 为两通信列车时速。 λ V1Δt)J0(2π （16）对上式进行仿真计算之后的结果如图 8 所示，在计算过程中假设发射机和接收机的多普勒频偏极值相等即 fMR = fMT 。此时从图 8 中可以看到，随着多普勒频偏的增大，信号的时域相关性的收敛程度越越大；同时当两通信列车的相对速度越大时，所产生的多普勒频偏也越大，此时信道的时变性也就越明显。数函关相自域时 1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 f f f MR = f MR = f MR = f MT =25 Hz v =160 km/h MT =35 Hz v =180 km/h MT =45 Hz v =200 km/h 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 时延/s 图 8 多普勒平移对无线信道的影响 3.2.2 单线铁路隧道环境中列车间直接通信信道的确定性模型假设隧道高为 H ，宽为 W ，发射机 Tx ，接收机的 Rx 天线高度均为 h ，天线均位于车顶靠隧道顶部中央位置，发射机接收机之间的距离为 d 。可得隧道环境中列车间直接通信信道的模型如下[22]所示。（1）直射路径，如图 9（a）所示。（2）视距内直射传播距离为 l = d2 = d ，可得直射路径的传输时延为 Δt = l/c ，c 为光速。（3）隧道顶和隧道底对电磁波的一次反射模型如图对于列车间直接通信而言，其通信设备具有一定的 9（a）所示。其中：计算机工程与应用www.ceaj.org

李淑娟，李茂青，高云波，等：列车间多频段直接通信系统设计及性能分析 2017，53（13） 109 H Tx h l3 θ1 θ1 θ θ l1 l4 l2 W Tx Rx h l7 l5 θ3 θ3 θ2 θ2 l8 l6 Rx （a）隧道顶、底对电磁波的反射（b）隧道侧壁对电磁波的发射图 9 隧道顶底以及隧道侧壁对电磁波的一次反射图 )2h 2 + d2 ] l1 + l2 = ( l3 + l4 = [ 2( sin θ = 2h l1 + l2 )H - h 2 + d2 2( )H - h l3 + l4 则两条路径的传播时延分别为： ) ，sin θ1 = l1 + l2 = l1 + l2 c ,Δt( Δt( ) l3 + l4 = l3 + l4 c （18）（19）隧道侧壁的一次反射模型如图 9（b）所示。其中： 2 l5 + l6 = ( W l7 + l8 = ( W sin θ2 = W l5 + l6 ) 2 + d2 2 +W ) 2 + d2 2 +W ， sin θ3 = W l7 + l8 则两条路径的传输时延分别为： ) l5 + l6 = l5 + l6 c ,Δt( Δt( 2 ) l7 + l8 = l7 + l8 c （20）（21）（4）隧道顶和隧道底对电磁波的二次反射模型如图 10（a）所示。其中： l1 + l2 + l3 = [ l4 + l5 + l6 = [ 2H sin θ = l1 + l2 + l3 h + H + ( )H - h 2 + d2 2H l4 + l5 + l6 ， sin θ1 = h + H + ( )H - h 2 + d2 ] ] 则两条路径的传输时延分别为： Δt( Δt( TxH h ) l1 + l2 + l3 = l1 + l2 + l3 l4 + l5 + l6 = l4 + l5 + l6 c ) c l4 θ1 θ1 l5 θ θ l3 l1 θ θ l2 θ1 θ1 l6 （22）（23） Rx h 图 10（a）隧道顶、底对电磁波的二次反射图（5）隧道侧壁对电磁波的二次反射模型如图 10（b）所示。其中： 2 + W +( ) W -W W l7 + l8 + l9 = é ù 2 ë û ) ( W -W 2 + W +W l10 + l11 + l12 = é ë 2 + d2 2 ù 2 û + d2 sin θ2 = 2W l7 + l8 + l9 ， sin θ3 = 2W l10 + l11 + l12 （24）则两条路径的传输时延分别为： Δt( Δt( ) l7 + l8 + l9 = l7 + l8 + l9 l10 + l11 + l12 = l10 + l11 + l12 c ) c （25） W Tx θ3 θ3 θ2 θ2 l10 l7 l11 l8 θ2 θ2 l9 θ3 θ3 l12 Rx 图 10（b）隧道侧壁对电磁波的二次反射图（6）对于隧道顶和隧道底，其单条奇数次反射路径模型中，反射次数 n 为奇数，反射路径共有 n + 1 段，则路径总长度为： Lo = l1 + l2 + … + ln + 1 = [ ] 传输线路与隧道底以及隧道顶的夹角为： 2h + ( n - 1 H 2 + d2 （26） ) sin θdi = 2h + ( ) n - 1 H Lo 对于隧道侧壁，路径总长度为： Lo = l1 + l2 + … + ln + 1 = ) 2 + ( ù n - 1 W û ) 2 ( W é ë ( 2 +W ) nW 2 + d2 + d2 = 传输路线与隧道侧壁的夹角为： = nW Lo n - 1 W Lo sin θci = W + ( ) （27）（28）（29）（7）同理，在单条偶数次反射路径模型中，反射次数 m 为偶数，反射路径共有 m + 1 段。对于隧道顶和隧道底而言，其路径总长度为： Le = l1 + l2 + … + lm + 1 = [ h + H - h + ( )m - 1 H 2 + d2 = ( ] )mH 2 + d2（30）传输路线与隧道顶和隧道底之间的夹角为： sin θdi = mH Le 对于隧道侧壁，路径总长度为： Le = l1 + l2 + … + lm + 1 = 2 + ( W 2 + W -W é ë ( )mW 2 + d2 )m - 1 W 2 + d2 = ù û 传输线与隧道侧壁夹角为： 2 + W -W 2 + ( Le sin θci = W n - 1 W ) = nW Le （31）（32）（33）计算机工程与应用www.ceaj.org

110 2017，53（13） Computer Engineering and Applications 计算机工程与应用 3.2.3 双线铁路隧道环境中列车间直接通信信道的确定性模型对于双线隧道而言，隧道顶和隧道底的反射与单线隧道一致，设隧道高度为 H ，隧道宽度为 2W ，分析双线隧道侧壁对电磁波的反射情况如下。（1）隧道侧壁对电磁波的单次反射模型如图 11所示。 ) 2 + d2 = W 2 + d2 2 l5 + l6 = ( W W l7 + l8 = é ë 2 +W 2 +( 2W -W 2 传输路线与两侧壁的夹角为：， sin θ3 = 2W l7 + l8 sin θ2 = W l5 + l6 2 ) ù û + d2 （34）（35） W Tx l7 l5 θ3 θ3 θ2 θ2 l8 l6 Rx 图 11 隧道侧壁对电磁波的单次反射模型（2）二次反射模型如图 12 所示。其中：根据以上分析，对通信信道的确定型模型进行仿真。以单线铁路隧道为例，隧道高 5.87 m，宽 4.88 m，接收机和发射机天线高 5.2 m（由于天线距离隧道顶比较近，故以隧道顶对信号的反射模型进行仿真分析），接收天线和发射天线都位于隧道中央，接收机与发射机之间的距离为 4 km。假设发射信号为类似于冲激信号的窄带信号 s(t) ，如图 13 所示[23]。 3.0 2.5 2.0 1.5 1.0 0.5 度幅 0 －4 －3 －2 －1 0 1 2 3 4 时间/ns 图 13 发射信号假设列车时速为 160 km/h，接收机和发射机的多普勒平移相等即 fMR = fMT = 25 Hz ，则接收信号为直射波和多次反射波的叠加，如图 14 和 15 所示。从图 14 和 15 可以看出反射次数越多，时延越大。 W l7 + l8 + l9 = é ë 2 + 2W +( ( 2W -W l10 + l11 + l12 = é ë ) 2W -W ù 2 û ) 2 + 2W +W sin θ2 = sin θ3 = l7 + l8 + l9 4W 4W l7 + l8 + l9 2 + d2 2 ù 2 û + d2 （36） 0 －50 －100 －150 B d / 平电收接 W Tx θ3 θ3 θ2 θ2 l10 l7 l11 l8 θ2 θ2 l9 θ3 θ3 l12 Rx 图 12 隧道侧壁对电磁波二次反射图（3）单条奇数次反射路径模型为： Lo = l1 + l2 + … + ln + 1 = [ ) 反射线与隧道侧壁的夹角为： W + ( n - 1 2W 2 + d2 （37） ] sin θdi = W + ( ) n - 1 2W Lo （38）（4）单条偶数次反射路径模型为： Le = l1 + l2 + … + lm + 1 = [ 2W + ( n - 1 2W 2 + d2（39） ) ] 反射路径与隧道侧壁的夹角为： sin θci = 2W + ( ) n - 1 2W Le = n2W Le （40） 0 20 40 60 80 100 120 140 160 180 200 时间/ns 图 14 反射 5 次后的接收信号时延 0 －50 －100 －150 B d / 平电收接 0 20 40 60 80 100 120 140 160 180 200 时间/ns 图 15 反射 15 次之后接收信号时延尽管确定性模型有能够逼真的反映出隧道无线信道多径效应对接收信号影响的优点，但是确定性模型只适合于简单计算而不适用于多路径的复杂计算以及实际仿真，另外，确定性模型对隧道的环境参量（隧道截面尺寸、隧道壁磁导率等）有较强的依赖性。因此，确定性计算机工程与应用www.ceaj.org-4-3-2-10123400.511.522.53

李淑娟，李茂青，高云波，等：列车间多频段直接通信系统设计及性能分析 2017，53（13） 111 模型只能作为研究隧道中无线电波传播规律的理论模型，不能作为仿真模型。受多径效应的影响，隧道中接收信号的包络变化具有随机性，需要用统计方法来分析，因此分析时需要建立无线信道的统计模型。 3.2.4 隧道中列车间直接通信信道的统计模型 3.2.4.1 无线信道冲激响应的统计模型对于一条无线传输信道而言，可以用随机脉冲响应 h( )t 来表示，如下式所示： h( )t = ∑ N - 1 k = 0 akδ( t - tk ejθk ) （41）其中，N 为信号多径数，ak 为第 k 条路径的随机幅度， tk 为第 k 条路径的随机到达时间，θk 为第 k 条路径的随机相位；ak 、tk 、θk 的统计特性随传播环境的不同而不同 [22]。所谓统计模型就是式（41）中的各个参数服从的某种统计特性。 3.2.4.2 ak 的统计模型通常随机幅度所服从的统计模型有瑞利（Rayleigh）分布、莱斯（Rice）分布、Nakagami 分布、威布尔分布和对数正态分布等。通过对隧道测量得出测量值与各分布的吻合程度，如表 1 所示[24]。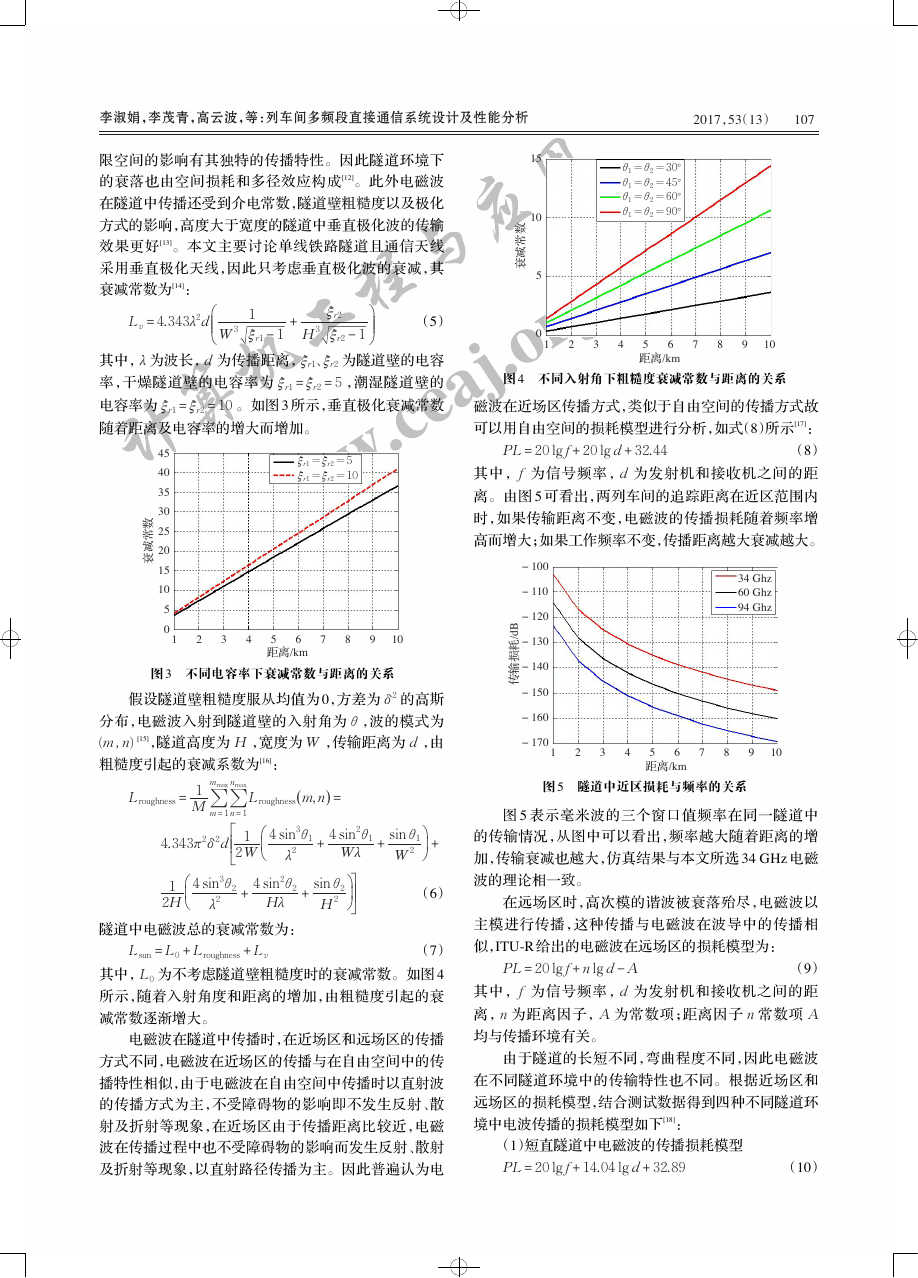表 1（a）衰落信号幅度包络分布模型与实测数据的吻合度（频率 2.4 GHz） % 统计模型瑞利分布莱斯分布 Nakagami 分布威布尔分布对数正态分布 LOS NLOS 0 91 2 7 0 88 0 4 6 2 表 1（b）衰落信号幅度包络分布模型与实测数据的吻合度（频率 5.8 GHz） % 统计模型瑞利分布莱斯分布 Nakagami 分布威布尔分布对数正态分布 LOS NLOS 1 84 2 8 0 90 2 4 2 2 从表中可以看出，对 2.4 GHz 和 5.8 GHz 两种频率的信号测试结果显示在视距范围内，两种频率的信号测试结果与 Rice 分布相吻合；在非视距情况下，两种频率的测试结果与 Rayleigh 分布相吻合。 N 假设接收端接受到的多径信号为： u( )t ejφ( )t = ∑ ∑ uk( )t ejφk( )t = ukI( )t cos φk( )t + ∑ k = 1 k k ukQ( )t sin φk( )t （42）其中，ukI( )t 是同相分量，ukQ( )t 为正交分量。瑞利（Rayleigh）分布：当前后行两列车的追踪距离在远场区范围内或者前后行列车在弯曲隧道内时，收发天线之间不存在直射信号，接收端接收到的多径信号叠加后的幅度包络服从瑞利分布即 u( )t 服从 p( )u = u δ2 -u2 2δ2，0 ≤ u ≤ +∞ e （43）其中，δ2 为同相分量和正交分量的方差[16]。莱斯（Rice）分布：当前后行两列车的追踪距离在近场区范围内时，收发天线之前存在直射信号，接收机接受到的信号幅度包络服从莱斯分布，此时可以认为在瑞利分布的基础上增加了一条直射信号，一般认为该信号为静态信号分量，相当于接收端在包络检波时再加一条直流分量。此时信号幅度 u( )t 服从 - æ çç è u2 + ρ2 2δ2 ö ÷÷ ø uρ δ2 æ ç è e Io （44），0 ≤ u ≤ +∞ p(u) = u δ2 )x 为第一类修正贝塞尔函 ö ÷ ø 其中，ρ 为直射信号强度，Io( 数，一般莱斯分布的唯一确定因素是莱斯因子 K = ρ2 2δ2 。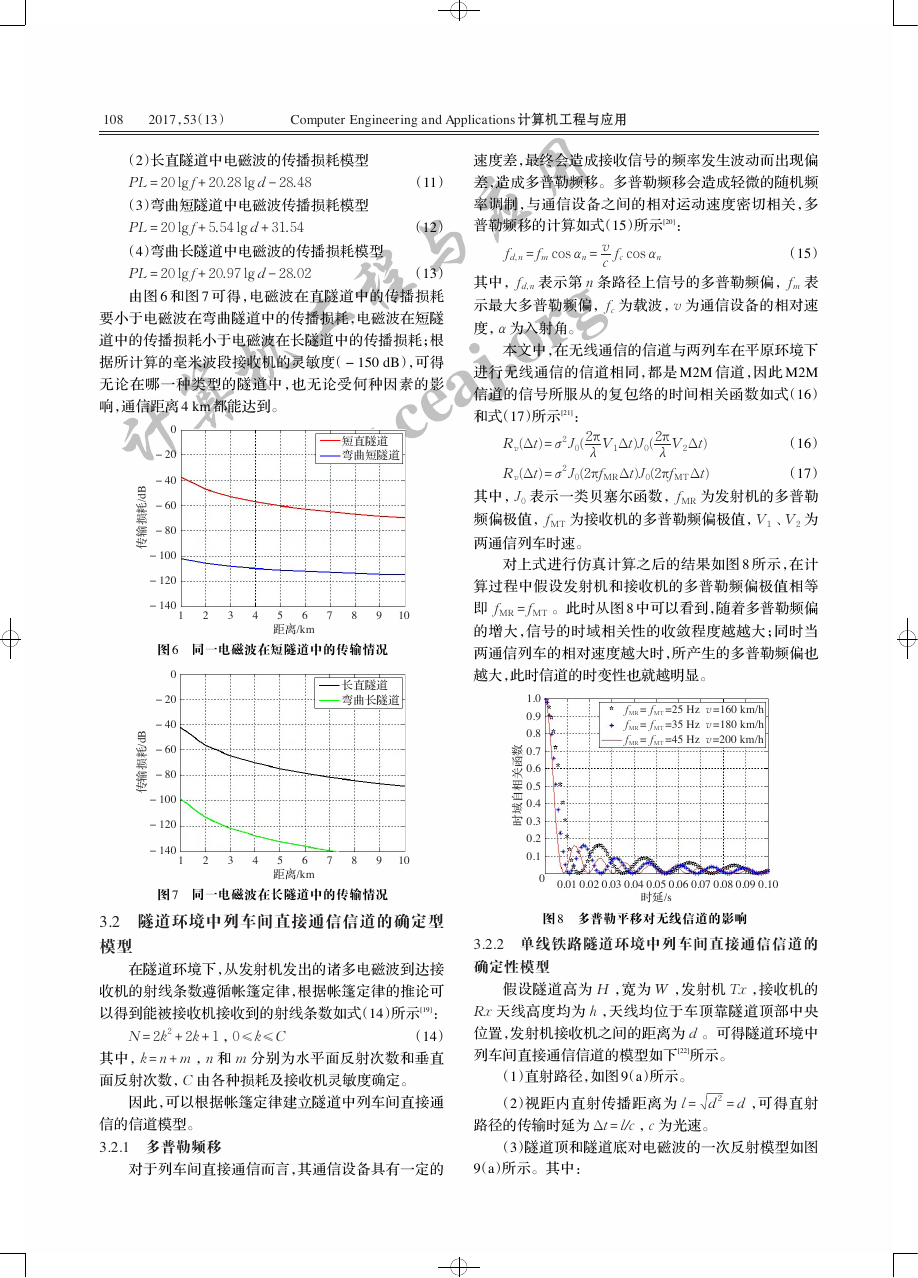图 16 为瑞利分布曲线，其中，δ2 是接收功率的时间均值，可以看出 δ2 越小接收信号范围越集中，同时说明信道条件较好，δ2 越大分布曲线越向右平移，说明信道条件相对较差。图 17 中 ρ 表示直射路径，ρ 越大表示发射机接收机之间的直射路径越强，可以看出 ρ = 0（不存在直射路径）时，莱斯曲线蜕变为瑞利曲线，ρ 越小曲 0.7 0.6 0.5 0.4 0.3 0.2 0.1 p δ2 = 0.5 δ2 = 1.5 δ2 = 3 ρ = 1 0.7 0.6 0.5 0.4 0.3 0.2 0.1 p ρ = 0 ，瑞利分布 ρ = 1 ρ = 1.5 δ2 = 1 0 1 2 3 4 5 6 7 u 0 1 2 3 u 4 5 6 图 16 瑞利分布曲线图 17 莱斯分布曲线计算机工程与应用www.ceaj.org

分享到：

赞收藏

资料库

论文研究-列车间多频段直接通信系统设计及性能分析.pdf

相关推荐

开发技术

热门标签

最新资料