基于线性滤波法的结构脉动风速模拟.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 基于自回归法的大跨度空间结构脉动风速模拟杨亚勤武汉理工大学土木工程与建筑学院，武汉（430070） E-mail: yyq2994@163.com 摘要：本文基于自回归法，编制了 MATLAB 程序，模拟了具有空间相关性的多点脉动风速时程曲线，并对所得风速时程作数理统计分析，得到的模拟功率谱与目标功率谱较为吻合。在此基础上对武汉火车站屋盖表面进行脉动风速时程模拟，得出其模拟的适合参数。关键词：大跨空间结构；自回归法；脉动风速时程模拟 1 引言在风振理论计算的过程中，许多风工程专家对水平阵风功率谱进行了研究，主要有 Davenport 风速谱、Kaimal 风速谱和 Simiu 风速谱等。我国《建筑结构荷载规范》GB50009-2001 采用 Davenport 脉动风速谱[1]。除水平功率谱外，还有垂直和横向功率谱。但与水平脉动风速谱相比，垂直和横向脉动风速谱要小得多，且互不相关，故本文在研究风振响应时只考虑水平脉动风速谱的影响[2]。利用时程分析法来进行结构的风振响应计算，首先要确定作用在结构上的脉动风荷载时程，对于大型复杂结构常通过刚性模型风洞试验获得节点上的风荷载时程，但是风洞试验一般需耗费大量的物力财力，不易实现。目前常用脉动风速时程模拟来获得风荷载时程，国内外模拟脉动风速时程主要有谐波叠加法和线性滤波器法两种。这两种方法都是基于蒙特卡洛思想，将脉动风速谱模拟成脉动风速时程，然后在准定常假设的基础上将风速时程转换成风荷载时程。它们从单一脉动风速时程模拟发展到多个相关风速时程的模拟，各有其优点和不足。其中线性滤波法中的自回归（AR）法因计算量小、速度快，广泛用于随机振动的时域模拟[3]。 2 谐波叠加法谐波叠加法是以一系列具有随机频率的三角函数加权叠加来逐渐逼近随机过程的离散化数值模拟方法。考虑一组 m 个 n 维随机过程 ( )ju t ( j = 1, 2 , , m )可模拟为： u t ( ) j = j N ∑ ∑ l = 1 k = 1 H n ( jk l ) 2 ∆ n cos( n t ' l + nθ ( jk l ) + φ kl ) j = 1, 2, (1) m , 式中，N 为足够大的正数； ( jkH n 可由 ( ) lnθ 截止频率； ( jk 所引入的随机频率。 ) 为不同点之间的相位角； ' n l ) S n 的乔利斯基分解得到； u pn 为 + ，其中 lnδ 为避免风速时程周期化 ∆ = = n l nδ N n n up l , 虽然谐波叠加法算法简单直观，适用于平稳高斯随机过程，但计算效率低。 3 线性滤波法用 AR 法模拟多维风速时程， M 个空间相关的脉动风速时程 [ ] u x y z t ( , , , ) u x y z t , , ), 1 ⎡ =⎣ ( , , u x y z t M ( , , , ) T ⎤ ⎦ 可由下式产生[4]： [ u x y z t ( , , ) , ] = p ∑ k 1 = [ ϕ k ][ u x y z t k t ( , ] − ∆ + ) , , [ N t ( ) ] (2) -1-

中国科技论文在线 http://www.paper.edu.cn 式中，p 为回归阶数；∆t 为模拟时间步长；[φk]为自回归系数矩阵， k=1,…,p； [N(t)]=[N1(t),…,NM(t)]T 其中 Ni(t)均值为 0，具有给定方差的正态随机过程。 3.1 求解回归系数矩阵随机风过程的协方差 R 与回归系数[φk]之间的关系可写成矩阵形式： [ R ] M P M × ⎡ = ⎣ R ⎤ ⎦ MP MP × [ ] ϕ M P M × （3）其中，Rij(k∆t)是 M×M 阶矩阵，i,j=1,…,p，k=1,…,p。通过以上各式可得出回归系数矩阵[φk]。 3.2 求 M 个随机过程 u x y z j , 1 ( , ⎡ ⎢ ⎢ ⎢ ⎣ M u x y z j ( , , t ) ∆ , t , ) ∆ （10） = ⎤ ⎥ ⎥ ⎥ ⎦ p ∑ k = 1 [ ϕ k ] ⎡ ⎢ ⎢ ⎢ ⎣ u x y z , 1 ( , M u x y z ( , , , ( , ( j − k ) ∆ t ) j − k ) ∆ t ) ⎤ ⎥ ⎥ ⎥ ⎦ ⎡ ⎢ + ⎢ ⎢ ⎣ N j 1( ( M N t ) ⎤∆ ⎥ ⎥ ⎥∆ ) ⎦ t j 计算时，假定初始时刻之前的风速为 0，即 t≤0 时，u(t)=0。 4 MATLAB 程序实现基于 AR 法的基本原理，应用 MATLAB 语言程序编制了考虑时间及空间相关性的水平脉动风速随机模拟程序，下面把编写过程作简要介绍[5]： (1)将所要生产脉动风速记录的节点坐标和平均风速 ( v z 提取出来写入“.txt”文件，并用 ) load 命令读入； (2)生成 m 行 n 列的标准正态分布随机数，其中 m 为空间点数，n 为整个时长的数据个数。应特别注意的是，在生成随机数之前要先初始化一个随机种子，防止相同的随机数； (3)根据时间序列的自回归模型求出考虑时间相关的脉动风速记录及相关的一些参数； (4)将 m 个无关的随机过程 ( u x y z t 转化为具有相关性的随机过程，即考虑脉动风速 , ) , , 的空间相关性； u t 记录整理并存储到文件里。主要步骤如下图所示： (5)将计算得到的脉动风速 ( ) -2-

中国科技论文在线 http://www.paper.edu.cn 输入相关参数 -平均风速； K -地面粗糙度长度；h -计算点数； p -计算阶数；SUMT-总的时间点数； 1 0v deltat-时间间隔；x()-所求点的 x 坐标；y()-所求点的 y 坐标；z()-所求点的 z 坐标。产生相关矩阵 R [nk,nk2]=size(kk); R=zeros(nk,nk); for m1=1:nk; for m2=1:nk R(m1,m2)=quadl(@(n)creatS(n, kk(m1,:),kk(m2,:),j,deltat),0.0001,10); end end 调用矩阵 RN 产生矩阵 [m1,m2]=size(Ψ); Ψ=zeros(m2,m2); Rx=zeros(m2,m2); n=m1./m2; for i=1:n; Ψ=Ψ((i‐1).*m2+1:i.*m2,:); R=creatR(i,deltat); Rx=Rx+Ψ*R; end Rn=creatR(0,deltat)‐Rx; L=chol(Rn)'; 自回归系数Ψk 的产生 R=creatR(1,deltat); [m1,m2]=size(R); Ry1=zeros(m1.*P,m2.*P); Ry2=zeros(1.*m1,m1.*P); a1=[0:1:P‐1,0:P‐1]; for i=1:P Rya(i,:)=a1(i:i+P‐1); end for i=1:P for j=1:P Ry1((i‐1).*m1+1:i.*m1,(j‐1).*m2 +1:j.*m2)=creatR(Rya(i,j),deltat); end end for i=1:P Ry2(1:m1,(i‐1).*m2+1:i.*m2) =creatR(i,deltat); end Ry2=Ry2'; Ψ=inv(Ry1)*Ry2 矩阵 Nt 的产生脉动风速时程 nt=normrnd(0,1,h,SUMT); Nt=L*nt; for i=1:P Rv=zeros(h,1); for j=1:i; Ψ=Ψ(j‐1).*h+1:j.*h,:); uk=uv(:,i‐j+1); Rv=Rv+Ψ*uk; end Rv=Rv+Nt(:,i); uv(:,i+1)=Rv; end for i=P+1:SUMT Rv=zeros(h,1); for j=1:P; Ψ=Ψ((j‐1).*h+1:j.*h,:); uk=uv(:,i‐j+1); Rv=Rv+Ψ*uk; end Rv=Rv+Nt(:,i); uv(:,i+1)=Rv; end Fig.1 The simulation flow chart of fluctuating wind velocity time-history 图 1 脉动风速时程模拟流程图 5 算例分析对空间点进行风速时程模拟，来验证 MATLAB 程序的正确性，模拟参数如下所示：场地类型为 B 类，平均风速为 25m/s（由基本风压 0.55N/m2 求得），回归阶数 p=4，模拟风速时程长度为 120s，时间步长为 0.1s。 5.1 空间四点风速时程模拟 -3-

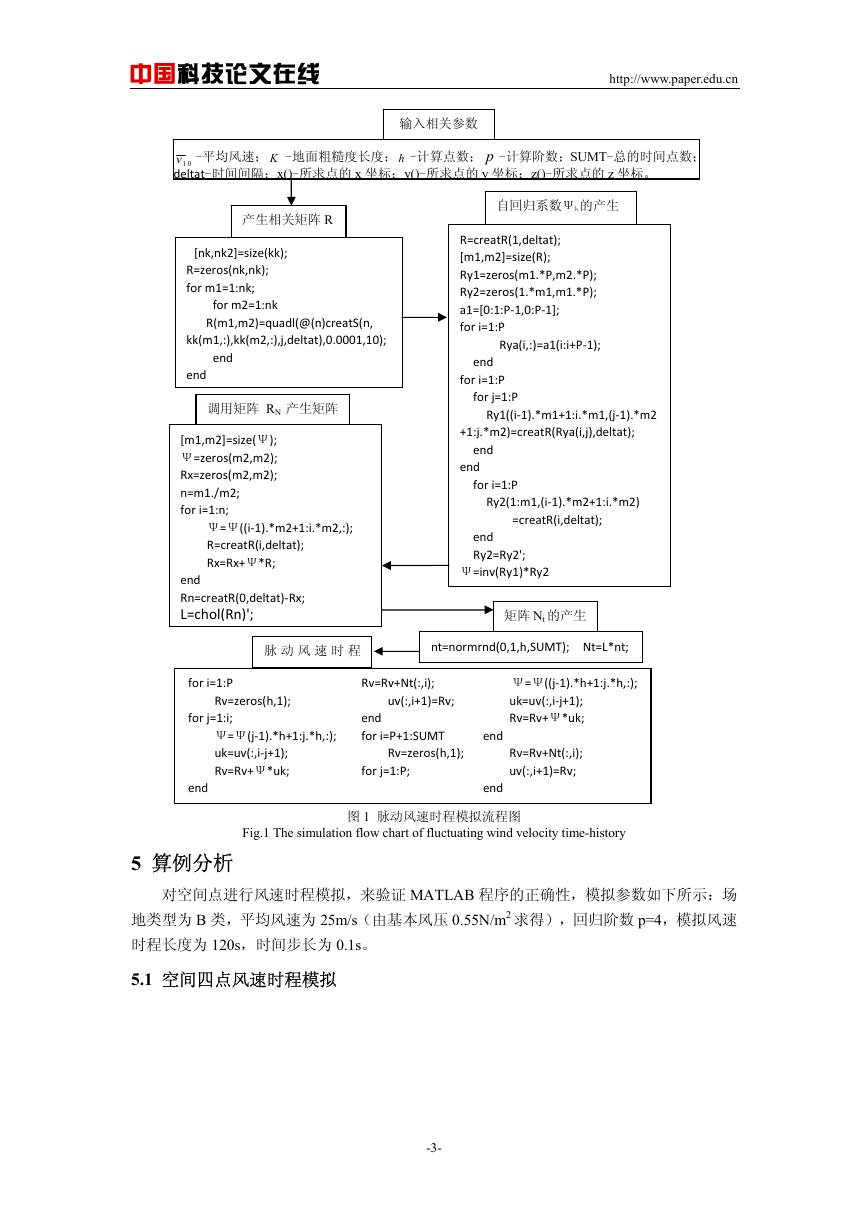
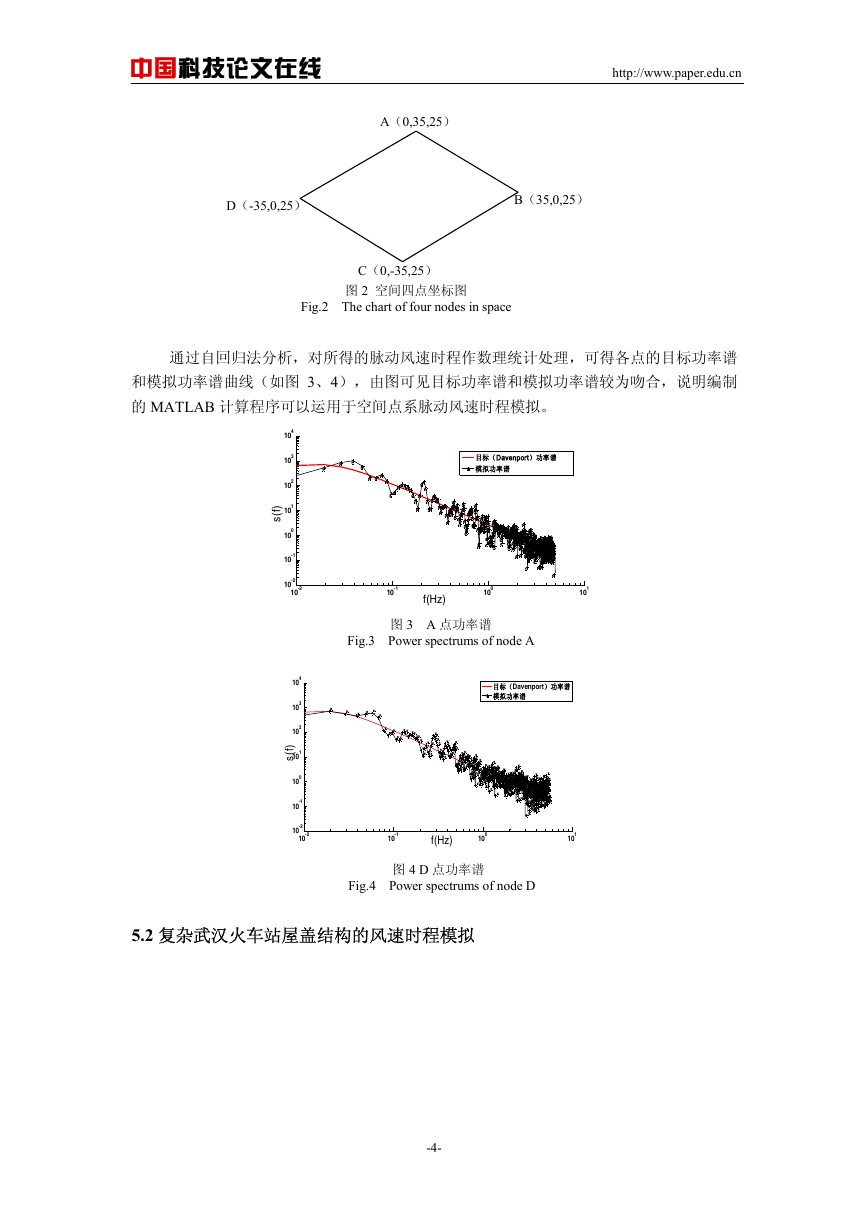
中国科技论文在线 http://www.paper.edu.cn A（0,35,25） D（-35,0,25） B（35,0,25） C（0,-35,25）图 2 空间四点坐标图 Fig.2 The chart of four nodes in space 通过自回归法分析，对所得的脉动风速时程作数理统计处理，可得各点的目标功率谱和模拟功率谱曲线（如图 3、4），由图可见目标功率谱和模拟功率谱较为吻合，说明编制的 MATLAB 计算程序可以运用于空间点系脉动风速时程模拟。 ) f ( s 104 103 102 101 100 10-1 10-2 10-2 104 103 102 ) f ( s 101 100 10-1 10-2 10-2 目标（Davenport）功率谱模拟功率谱 10-1 f(Hz) 100 101 图 3 A 点功率谱 Fig.3 Power spectrums of node A 目标（Davenport）功率谱模拟功率谱 10-1 f(Hz) 100 101 Fig.4 Power spectrums of node D 图 4 D 点功率谱 5.2 复杂武汉火车站屋盖结构的风速时程模拟 -4-

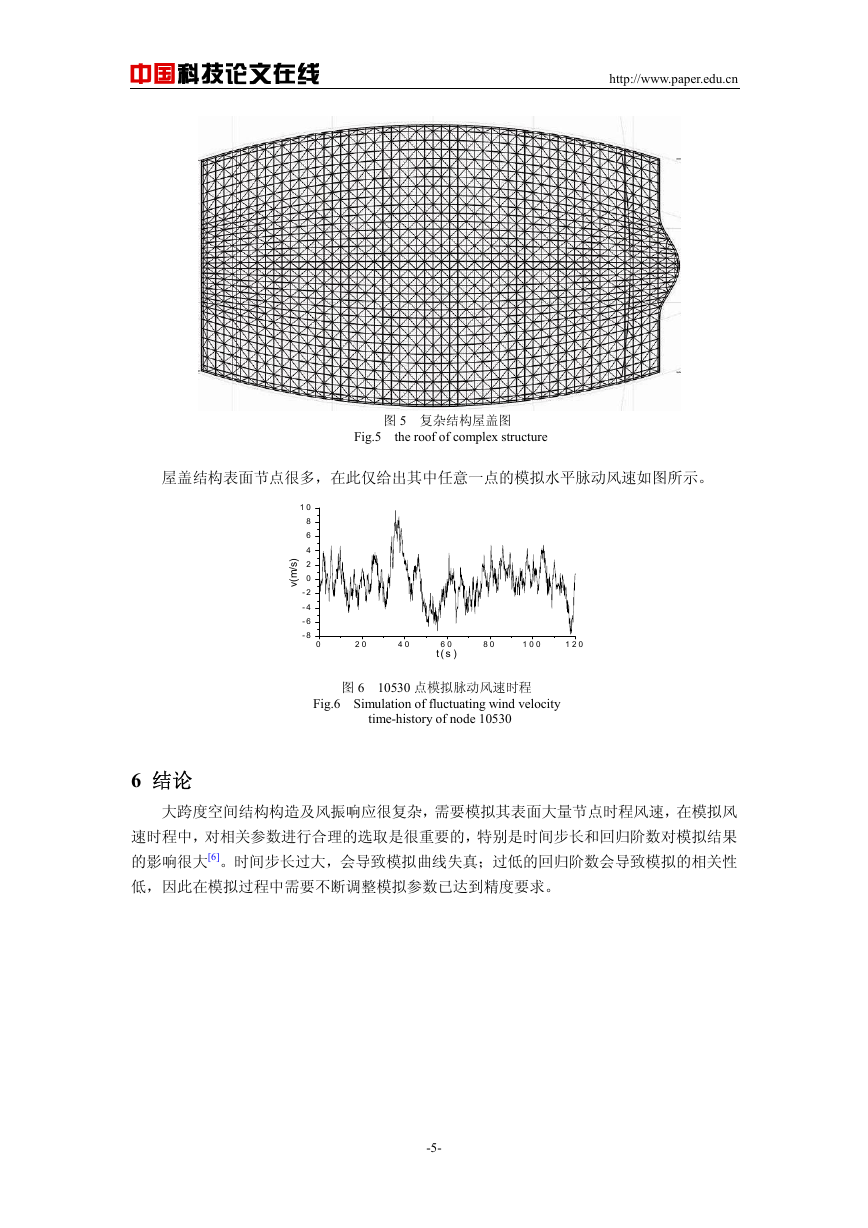
中国科技论文在线 http://www.paper.edu.cn 图 5 复杂结构屋盖图 Fig.5 the roof of complex structure 屋盖结构表面节点很多，在此仅给出其中任意一点的模拟水平脉动风速如图所示。 1 0 8 6 4 2 0 - 2 - 4 - 6 - 8 ) s / m ( v 0 2 0 4 0 6 0 t( s ) 8 0 1 0 0 1 2 0 图 6 10530 点模拟脉动风速时程 Fig.6 Simulation of fluctuating wind velocity time-history of node 10530 6 结论大跨度空间结构构造及风振响应很复杂，需要模拟其表面大量节点时程风速，在模拟风速时程中，对相关参数进行合理的选取是很重要的，特别是时间步长和回归阶数对模拟结果的影响很大[6]。时间步长过大，会导致模拟曲线失真；过低的回归阶数会导致模拟的相关性低，因此在模拟过程中需要不断调整模拟参数已达到精度要求。 -5-

中国科技论文在线 http://www.paper.edu.cn 参考文献 [1] 中华人民共和国国家标准,GB50009-2001,建筑结构荷载规范[S],北京:中国建筑工业出版社，2002. [2] 张相庭. 结构风压和风振计算[M].上海:同济大学出版社,1985. [3] 王之宏.风荷载的模拟研究[J]. 建筑结构学报[J].1994,15(1):44-52. [4] 舒新玲,周岱. 风速时程 AR 模型及其快速实现[J]. 空间结构,2003(12):27-32. [5] 袁波, 应惠清, 徐佳伟. 基于线性滤波法的脉动风速模拟及其 MATLAB 程序实现[J]. 结构工程师,2007,23(4):55-61. [6] 王修琼,张相庭. 混合回归模型及其在高层建筑风响应时域分析中的应用[J]. 振动与冲击,2000,19(1):5-7. Simulation of fluctuating wind velocity of Long-span Spatial structures using auto-regressive method School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan, Yang Yaqin China (430070) Abstract In this paper, MATLAB program is compiled based on auto-regressive method to simulate time history curve of fluctuating wind speed of multi-points which have space correlation. The simulated power spectra are obtained by mathematical statistics on discrete values of wind speed, which are consistent with aim power spectra. Wuhan railway station is taken as example, time history curves of fluctuating wind speed of surface nodes in roof are simulated. The proper parameters are determined by analyse. Keywords: long-span spatial structures, auto-regressive method, time history simulation of fluctuating wind speed -6-

资料库

基于线性滤波法的结构脉动风速模拟.pdf

相关推荐

开发技术

热门标签

最新资料