论文研究-OFDM-OQAM系统实现方法及抗双选信道特性分析 .pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.37M 资料格式：pdf 举报版权申诉

weixin_39841365-11547774-4744302543400602529.pdf-第1页.png

第1页 / 共9页

weixin_39841365-11547774-4744302543400602529.pdf-第2页.png

第2页 / 共9页

weixin_39841365-11547774-4744302543400602529.pdf-第3页.png

第3页 / 共9页

weixin_39841365-11547774-4744302543400602529.pdf-第4页.png

第4页 / 共9页

weixin_39841365-11547774-4744302543400602529.pdf-第5页.png

第5页 / 共9页

weixin_39841365-11547774-4744302543400602529.pdf-第6页.png

第6页 / 共9页

weixin_39841365-11547774-4744302543400602529.pdf-第7页.png

第7页 / 共9页

weixin_39841365-11547774-4744302543400602529.pdf-第8页.png

第8页 / 共9页

文本预览

5 10 15 20 25 30 35 40 中国科技论文在线 OFDM-OQAM 系统实现方法及抗双选信道 http://www.paper.edu.cn 特性分析谢越，宁晓燕** （哈尔滨工程大学信息与通信工程学院，哈尔滨市 150001）摘要：OFDM 技术在多载波通信技术中占据主导地位，但本身也具有很多缺点，如频谱利用率低、对同步要求严格及对载波频率偏移敏感等问题。本文对 OFDM-OQAM 技术进行了讨论，其通过将复数域正交条件放宽至实数域，为引入具有良好时频聚焦特性的滤波器创造了条件，从而在不添加 CP 的前提下具有比 OFDM 更为优越的特性。首先，在对系统模型进行讨论的基础上，文章对 OFDM-OQAM 系统中多相网络及频域扩展两种实现方法进行了讨论，然后从频域均衡和计算复杂度等方面对两种方法进行了比较和分析。最后在高白信道和双选信道下对 OFDM-OQAM 和 OFDM 两系统的误码率及信号功率谱密度特性进行了仿真，验证了 OFDM-OQAM 技术在抗频率选择性衰落和改善频谱利用率方面的优势。最后从计算复杂度的角度论述了多相网络方法的优越性。关键词：OFDM；OFDM-OQAM；多相网络；计算复杂度中图分类号：TN914.3 Implementation of OFDM-OQAM system and performance analysis against doubly selective channel XIE Yue, NING Xiaoyan 150001) (Information and Communication Engineering School, Harbin Engineering University, Harbin Abstract: Among many other multicarrier techniques, Orthogonal Frequency Division Multiplex(OFDM) is dominant. But OFDM has some shortcomings such as low spectral density, strict synchronicity requirement and sensitivity to carrier frequency shift. This paper selects Offset Quadrature Amplitude Modulation based Orthogonal Frequency Division Multiplex(OFDM-OQAM) for discussion,which allows the introduction of a well-localized pulse shape by relaxing the orthogonal condition from complex comain to real. And thus, OFDM-OQAM has many advantages over OFDM without adding Cyclic Prefix(CP). First of all, two implementations of polyphase network and frequency spread of OFDM-OQAM system are discussed, and then compared and analyzed in terms of frequency domain equalization and computational complexity. After that, the simulation result of bit error rate and signal power spectral density of OFDM and OFDM-OQAM in some aspects such as improvement of spectral utilization and robustness against frequency selective fading channel are given. And the dominant position of polyphase network is verified in terms of computational complexity. Keywords: OFDM; OFDM-OQAM; polyphase network; computational complexity 0 引言为满足移动通信中高质量、高速率传输的需求，能够提供高速数据传输的多载波调制技术就成为一种很有吸引力的方案。其中 OFDM 技术基于实现复杂度较低及通过加入 CP 降低了符号间干扰（Inter Symbol Interference，ISI）等优点得到了广泛的应用。然而，OFDM 也存在一些技术缺陷，如 CP 的存在造成了频谱利用率和传输功率的损失、带外泄露严重[1]、作者简介：谢越（1993-），女，硕士研究生，主要研究方向：OFDM-OQAM 系统实现及原型滤波器特性分析通信联系人：宁晓燕（1984-），女，讲师，硕导，主要研究方向：广义多载波技术，通信电子战波形设计. E-mail: ningxiaoyan@hrbeu.edu.cn - 1 -

45 50 55 中国科技论文在线对载波频率偏移十分敏感，容易导致载波间干扰（Inter Carrier Interference，ICI）[2]等等。鉴于 OFDM 系统本身存在的一些问题，在下一代移动通信技术中，为进一步提升传输速率并应对新场景的需求，OFDM-OQAM 技术受到了越来越多的重视。目前 OFDM-OQAM 技术也已被 METIS、5GNOW 和 PHYDYAS 等国外计划或组织列为重点研究内容[3]，且被我国 IMT-2020（5G）推进组纳入了 5G 物理层调制波形的主要候选方案。 http://www.paper.edu.cn 与 OFDM 相比，OFDM-OQAM 将复数域正交条件放宽至实数域，通过引入具有良好时频聚焦特性的滤波器，达到了降低带外能量泄露和提高频谱利用率的目的。由于滤波器函数在时域和频域的带外衰减都更理想，OFDM-OQAM 系统抗 ISI 和 ICI 的能力也比较强[4]。早期的 OFDM-OQAM 系统由于实现复杂度过高，其研究停滞不前，但随着基于 IFFT/FFT 的系统低复杂度实现方案的提出，OFDM-OQAM 技术有望投入应用。本文的主要内容如下：选取 OFDM-OQAM 系统作为研究对象，以 OFDM-OQAM 系统低复杂度实现方法的对比分析作为研究目的，从计算复杂度和频域均衡等角度对多相网络和频域扩展两种方法进行讨论。下面将首先对系统模型进行介绍，之后对 OFDM-OQAM 的两种实现方法进行具体的研究，并在最后针对 OFDM 和 OFDM-OQAM 在信号带外特性、系统实现复杂度和具体信道环境下的误码率特性进行仿真和对比分析。 1 OFDM-OQAM 系统模型 60 基于 OQAM 调制的特殊形式，OFDM-OQAM 系统的等效基带发送信号可写成如下的分析形式[5]：   s t   N 1    m   0 n a g R m n m n ,2 ,   t  a g I m n m n ,2 , 1    t 其中： N 为子载波个数； ,m na 表示第 n 个 OFDM-OQAM 符号中的第 m 个子载波上发送的数据符号，其值为实；   ,m n 的基函数，可通过以下时频变换得到： t 表示时频格点坐标为 ,m ng  65 70 其中： 0v 表示子载波间隔； 0 表示相邻符号的实虚部间的偏移量。将式（2）中基函数的表示带入（1）可得：  g t n 0 m ng ,   t mv t 0   j2π e e  πj 2  m n    N 1    s t   假设采样时间为 sT ，对   m    n 0 m n 2   j π 2  e j2π mv t 0 e a R m n ,    g t  2 n  0   j a I m n ,  g t  2 n   0 0     s t 在时间 nT nT  0 ,  内进行采样可得：  0  a g nT kT R m l s ,    lT   j a g nT kT I m l s ,      lT  T 2        s nT kT s     N 1    m   0 l j π 2  e  m l 2      j2π mk N e  其中： k   N / 2,..., N / 2 1  。令  s nT kT s    s nN k      s n k 和 p n l   ，则由上式（4）可得：   s n k     p    p   g pT kT s      g pT kT s      N 1   0 m  T 2 m n 2   2 p j π 2  e j2π mk N  e a R m n p  , j a I m n p  , m n 2   2 p  j π 2  e       N 1   m  0    e j2π mk N    - 2 - （1）（2）（3）（4）（5）

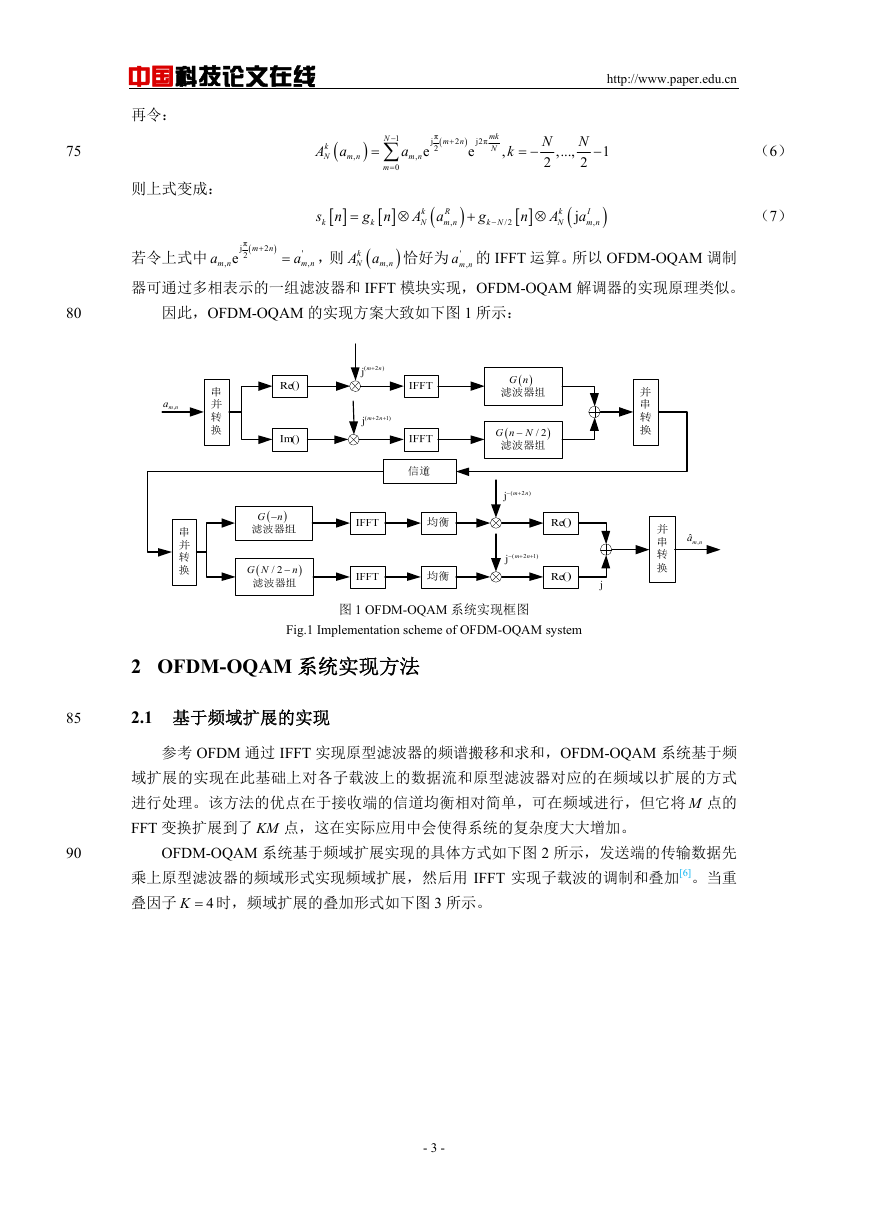
中国科技论文在线 http://www.paper.edu.cn 再令： 75 则上式变成：  A a k N m n ,   N 1   m  0 j π 2  e a m n , m n 2   j2π mk N e , k   N 2 ,..., N 2  1   s n k    g n k   A a k N R m n ,   g k N  /2   n  A k N  a j I m n ,  （6）（7） m n 2   πj 2   ，则  a ' m n , e a m n , 若令上式中 ,m na 的 IFFT 运算。所以 OFDM-OQAM 调制器可通过多相表示的一组滤波器和 IFFT 模块实现，OFDM-OQAM 解调器的实现原理类似。因此，OFDM-OQAM 的实现方案大致如下图 1 所示： A a 恰好为 ' k N m n , 80 ,m na j m n ( 2 ) j m n ( 2 1)  G n   G N  / 2 n   G n G n N  / 2   j m n ( 2 )   j m n ( 2  1)  图 1 OFDM-OQAM 系统实现框图 Fig.1 Implementation scheme of OFDM-OQAM system 2 OFDM-OQAM 系统实现方法 85 2.1 基于频域扩展的实现 ,ˆm na j 参考 OFDM 通过 IFFT 实现原型滤波器的频谱搬移和求和，OFDM-OQAM 系统基于频域扩展的实现在此基础上对各子载波上的数据流和原型滤波器对应的在频域以扩展的方式进行处理。该方法的优点在于接收端的信道均衡相对简单，可在频域进行，但它将 M 点的 FFT 变换扩展到了 KM 点，这在实际应用中会使得系统的复杂度大大增加。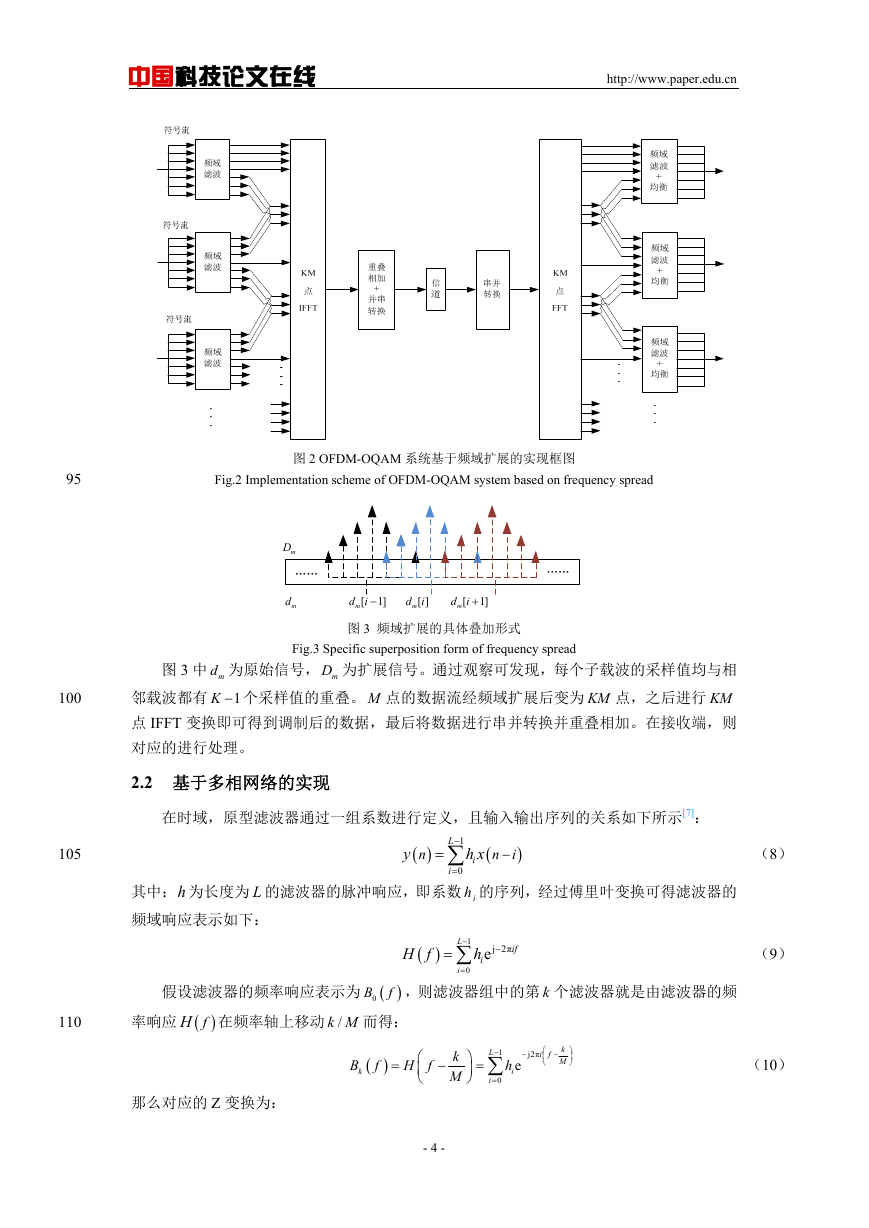 OFDM-OQAM 系统基于频域扩展实现的具体方式如下图 2 所示，发送端的传输数据先乘上原型滤波器的频域形式实现频域扩展，然后用 IFFT 实现子载波的调制和叠加[6]。当重叠因子 4K  时，频域扩展的叠加形式如下图 3 所示。 90 - 3 -

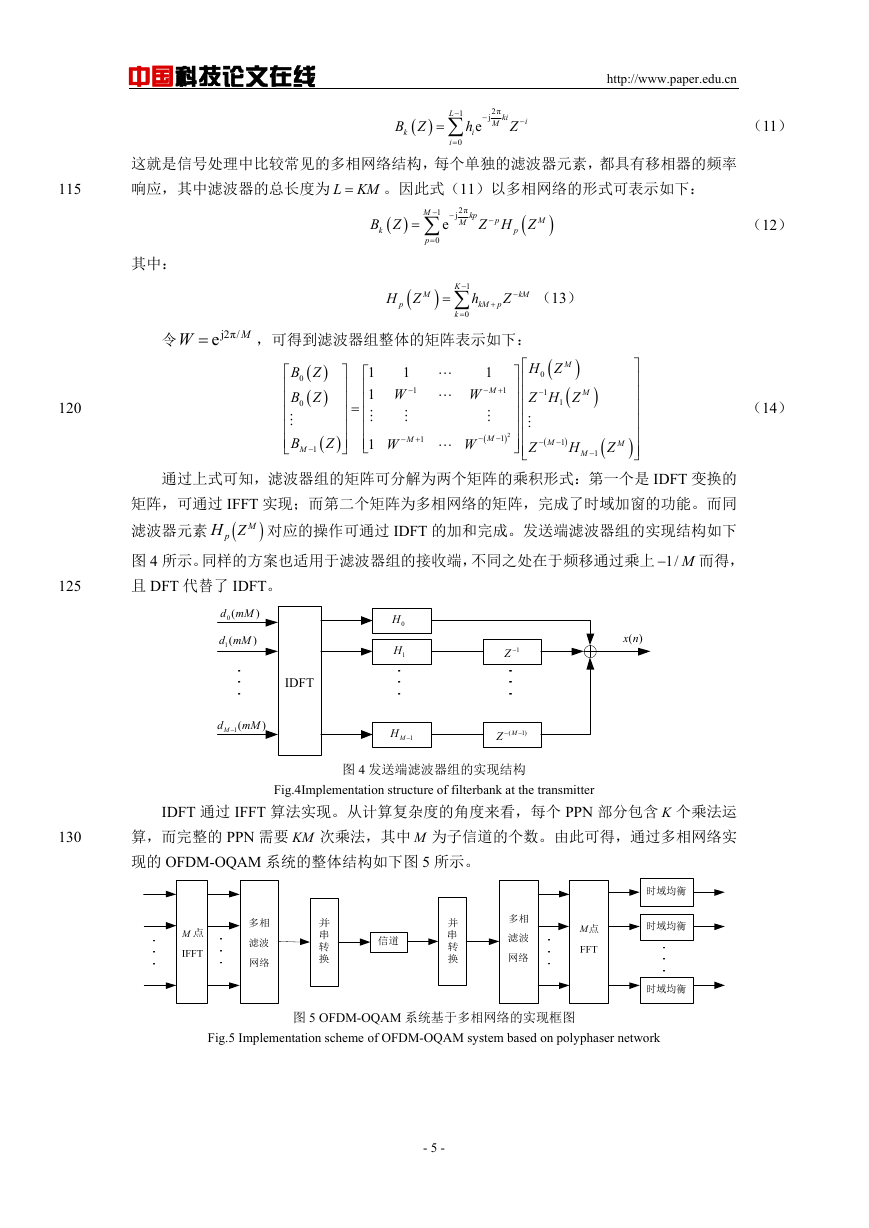
中国科技论文在线 http://www.paper.edu.cn 95 Fig.2 Implementation scheme of OFDM-OQAM system based on frequency spread 图 2 OFDM-OQAM 系统基于频域扩展的实现框图 mD …… md md i  [ 1] [ ]md i md i  [ 1] 图 3 频域扩展的具体叠加形式 …… 100 Fig.3 Specific superposition form of frequency spread 图 3 中 md 为原始信号， mD 为扩展信号。通过观察可发现，每个子载波的采样值均与相邻载波都有 1K  个采样值的重叠。 M 点的数据流经频域扩展后变为 KM 点，之后进行 KM 点 IFFT 变换即可得到调制后的数据，最后将数据进行串并转换并重叠相加。在接收端，则对应的进行处理。 2.2 基于多相网络的实现在时域，原型滤波器通过一组系数进行定义，且输入输出序列的关系如下所示[7]： 105 y   n L 1    i  0 h x i  n i   其中：h 为长度为 L 的滤波器的脉冲响应，即系数 ih 的序列，经过傅里叶变换可得滤波器的频域响应表示如下：  H f  L 1    i  0 if j 2π  h i e 假设滤波器的频率响应表示为   fH 在频率轴上移动 /k M 而得：率响应  0B f ，则滤波器组中的第 k 个滤波器就是由滤波器的频 110 那么对应的 Z 变换为：  B f k    H f    k M - 4 -  i j2π  f   k M    h i e L 1        0 i （8）（9）（10）

（11）（12）（14）中国科技论文在线 http://www.paper.edu.cn  B Z k   j 2π M ki h i e  i Z L 1    i  0 115 这就是信号处理中比较常见的多相网络结构，每个单独的滤波器元素，都具有移相器的频率响应，其中滤波器的总长度为 L KM 。因此式（11）以多相网络的形式可表示如下：其中：令 W  e j2π/ M 120  B Z k  M 1    p  0  j 2π M kp e p   Z H Z p M   H Z p M  K 1    k  0 h kM p  Z  kM （13）    B Z 0  B Z 0 ，可得到滤波器组整体的矩阵表示如下：              Z          B   M 1   1     1   1 W 1           1 M   M  W W W  M  Z  1       1  1  1  2 0 M   H Z  Z H Z 1  1 M    M  1  H M 1   M Z          通过上式可知，滤波器组的矩阵可分解为两个矩阵的乘积形式：第一个是 IDFT 变换的矩阵，可通过 IFFT 实现；而第二个矩阵为多相网络的矩阵，完成了时域加窗的功能。而同滤波器元素  p ZH 对应的操作可通过 IDFT 的加和完成。发送端滤波器组的实现结构如下图 4 所示。同样的方案也适用于滤波器组的接收端，不同之处在于频移通过乘上 1/ M 且 DFT 代替了 IDFT。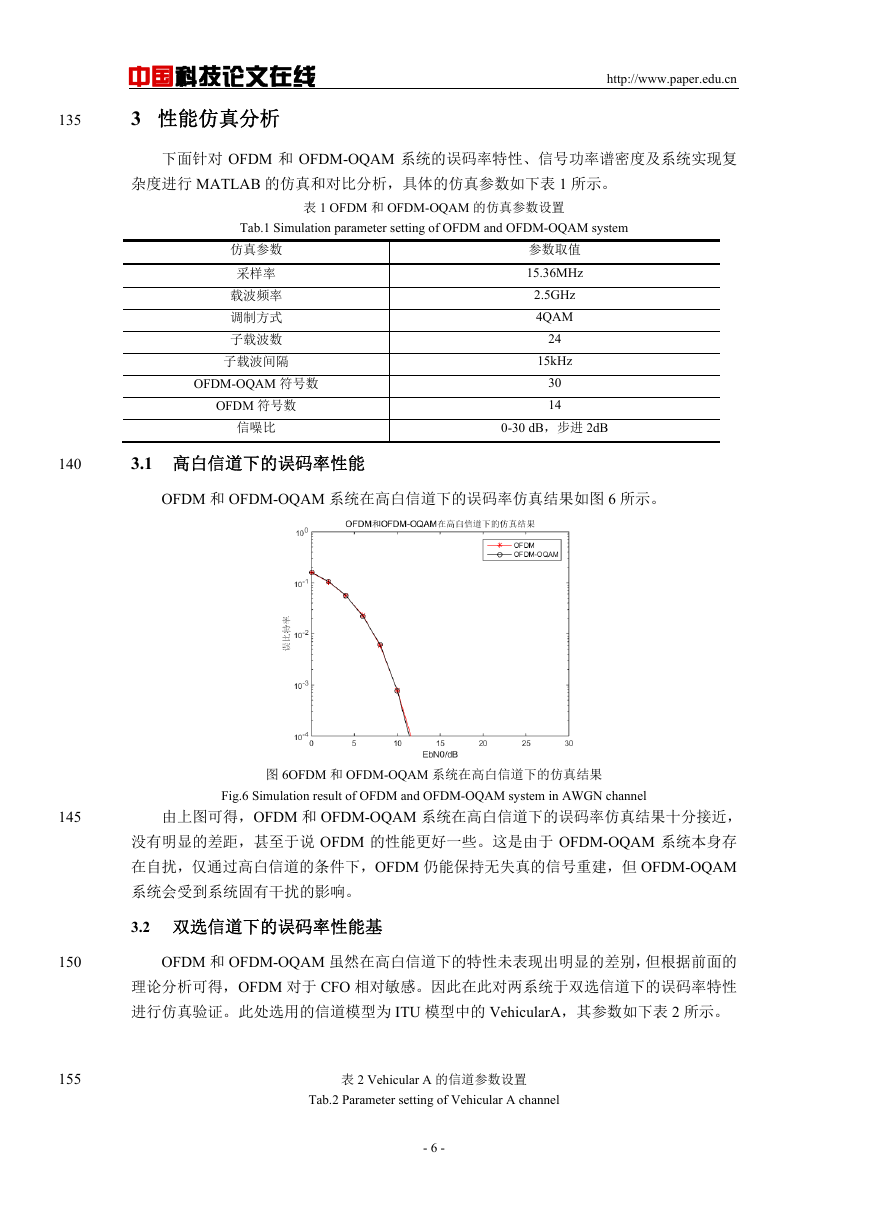 M 而得， 125 d mM 0( ) d mM 1( ) Md mM 1( ) IDFT 0H 1H 1Z  x n ( ) 1MH  ( 1)MZ   图 4 发送端滤波器组的实现结构 Fig.4Implementation structure of filterbank at the transmitter 130 IDFT 通过 IFFT 算法实现。从计算复杂度的角度来看，每个 PPN 部分包含 K 个乘法运算，而完整的 PPN 需要 KM 次乘法，其中 M 为子信道的个数。由此可得，通过多相网络实现的 OFDM-OQAM 系统的整体结构如下图 5 所示。 M M 图 5 OFDM-OQAM 系统基于多相网络的实现框图 Fig.5 Implementation scheme of OFDM-OQAM system based on polyphaser network - 5 -

中国科技论文在线 3 性能仿真分析 135 http://www.paper.edu.cn 下面针对 OFDM 和 OFDM-OQAM 系统的误码率特性、信号功率谱密度及系统实现复杂度进行 MATLAB 的仿真和对比分析，具体的仿真参数如下表 1 所示。表 1 OFDM 和 OFDM-OQAM 的仿真参数设置 Tab.1 Simulation parameter setting of OFDM and OFDM-OQAM system 仿真参数采样率载波频率调制方式子载波数子载波间隔 OFDM-OQAM 符号数 OFDM 符号数信噪比参数取值 15.36MHz 2.5GHz 4QAM 24 15kHz 30 14 0-30 dB，步进 2dB 140 3.1 高白信道下的误码率性能 OFDM 和 OFDM-OQAM 系统在高白信道下的误码率仿真结果如图 6 所示。 145 150 155 图 6OFDM 和 OFDM-OQAM 系统在高白信道下的仿真结果 Fig.6 Simulation result of OFDM and OFDM-OQAM system in AWGN channel 由上图可得，OFDM 和 OFDM-OQAM 系统在高白信道下的误码率仿真结果十分接近，没有明显的差距，甚至于说 OFDM 的性能更好一些。这是由于 OFDM-OQAM 系统本身存在自扰，仅通过高白信道的条件下，OFDM 仍能保持无失真的信号重建，但 OFDM-OQAM 系统会受到系统固有干扰的影响。 3.2 双选信道下的误码率性能基 OFDM 和 OFDM-OQAM 虽然在高白信道下的特性未表现出明显的差别，但根据前面的理论分析可得，OFDM 对于 CFO 相对敏感。因此在此对两系统于双选信道下的误码率特性进行仿真验证。此处选用的信道模型为 ITU 模型中的 VehicularA，其参数如下表 2 所示。表 2 Vehicular A 的信道参数设置 Tab.2 Parameter setting of Vehicular A channel - 6 -

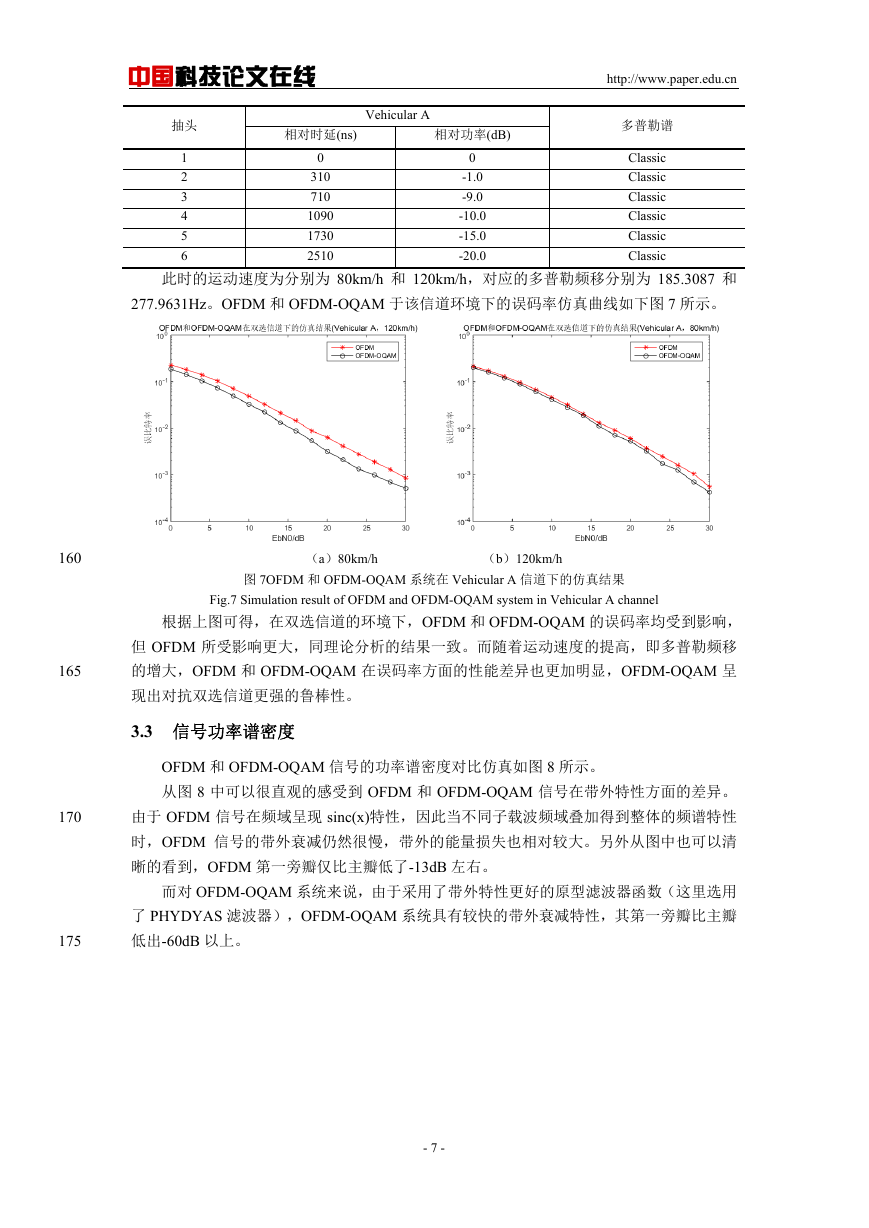
中国科技论文在线 http://www.paper.edu.cn 抽头 1 2 3 4 5 6 Vehicular A 相对时延(ns) 相对功率(dB) 0 310 710 1090 1730 2510 0 -1.0 -9.0 -10.0 -15.0 -20.0 多普勒谱 Classic Classic Classic Classic Classic Classic 此时的运动速度为分别为 80km/h 和 120km/h，对应的多普勒频移分别为 185.3087 和 277.9631Hz。OFDM 和 OFDM-OQAM 于该信道环境下的误码率仿真曲线如下图 7 所示。 160 165 170 175 （a）80km/h （b）120km/h 图 7OFDM 和 OFDM-OQAM 系统在 Vehicular A 信道下的仿真结果 Fig.7 Simulation result of OFDM and OFDM-OQAM system in Vehicular A channel 根据上图可得，在双选信道的环境下，OFDM 和 OFDM-OQAM 的误码率均受到影响，但 OFDM 所受影响更大，同理论分析的结果一致。而随着运动速度的提高，即多普勒频移的增大，OFDM 和 OFDM-OQAM 在误码率方面的性能差异也更加明显，OFDM-OQAM 呈现出对抗双选信道更强的鲁棒性。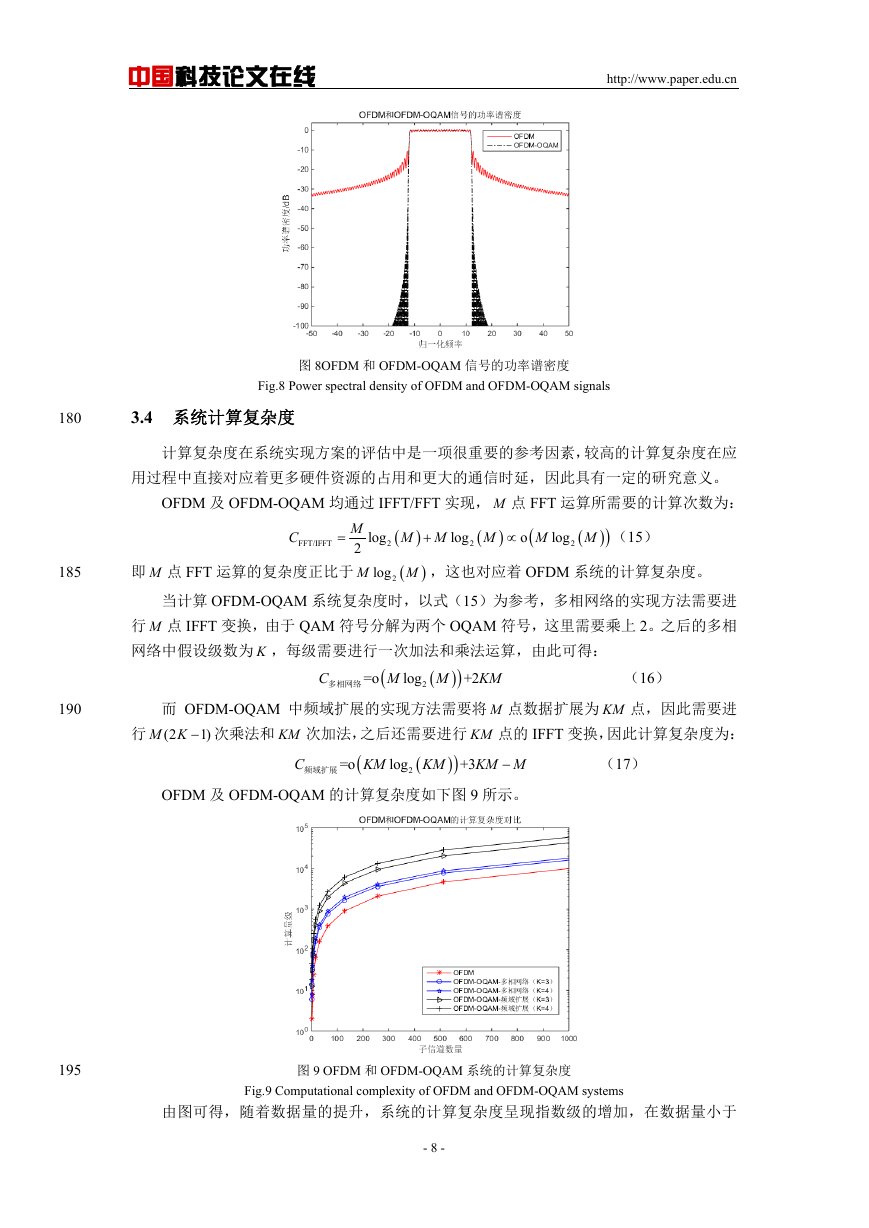 3.3 信号功率谱密度 OFDM 和 OFDM-OQAM 信号的功率谱密度对比仿真如图 8 所示。从图 8 中可以很直观的感受到 OFDM 和 OFDM-OQAM 信号在带外特性方面的差异。由于 OFDM 信号在频域呈现 sinc(x)特性，因此当不同子载波频域叠加得到整体的频谱特性时，OFDM 信号的带外衰减仍然很慢，带外的能量损失也相对较大。另外从图中也可以清晰的看到，OFDM 第一旁瓣仅比主瓣低了-13dB 左右。而对 OFDM-OQAM 系统来说，由于采用了带外特性更好的原型滤波器函数（这里选用了 PHYDYAS 滤波器），OFDM-OQAM 系统具有较快的带外衰减特性，其第一旁瓣比主瓣低出-60dB 以上。 - 7 -

中国科技论文在线 http://www.paper.edu.cn 图 8OFDM 和 OFDM-OQAM 信号的功率谱密度 Fig.8 Power spectral density of OFDM and OFDM-OQAM signals 180 3.4 系统计算复杂度计算复杂度在系统实现方案的评估中是一项很重要的参考因素，较高的计算复杂度在应用过程中直接对应着更多硬件资源的占用和更大的通信时延，因此具有一定的研究意义。 OFDM 及 OFDM-OQAM 均通过 IFFT/FFT 实现， M 点 FFT 运算所需要的计算次数为： 185 C FFT/IFFT   M M   log 2  M   o  M log  M 2   （15） 2 log M 2 logM 即 M 点 FFT 运算的复杂度正比于当计算 OFDM-OQAM 系统复杂度时，以式（15）为参考，多相网络的实现方法需要进行 M 点 IFFT 变换，由于 QAM 符号分解为两个 OQAM 符号，这里需要乘上 2。之后的多相网络中假设级数为 K ，每级需要进行一次加法和乘法运算，由此可得： M ，这也对应着 OFDM 系统的计算复杂度。 2   C 多相网络 =o  M log 2  M   +2 KM （16） 190 而 OFDM-OQAM 中频域扩展的实现方法需要将 M 点数据扩展为 KM 点，因此需要进 M K  次乘法和 KM 次加法，之后还需要进行 KM 点的 IFFT 变换，因此计算复杂度为：行 (2 1) C 频域扩展 =o  KM log  KM 2   +3 KM M （17） OFDM 及 OFDM-OQAM 的计算复杂度如下图 9 所示。 195 图 9 OFDM 和 OFDM-OQAM 系统的计算复杂度 Fig.9 Computational complexity of OFDM and OFDM-OQAM systems 由图可得，随着数据量的提升，系统的计算复杂度呈现指数级的增加，在数据量小于 - 8 -

分享到：

赞收藏

资料库

论文研究-OFDM-OQAM系统实现方法及抗双选信道特性分析 .pdf

相关推荐

开发技术

热门标签

最新资料