非线性控制系统的反馈线性化.pdf-资料库

007ts-1143201-16359647501073865723.pdf-第1页.png

第1页 / 共13页

007ts-1143201-16359647501073865723.pdf-第2页.png

第2页 / 共13页

007ts-1143201-16359647501073865723.pdf-第3页.png

第3页 / 共13页

007ts-1143201-16359647501073865723.pdf-第4页.png

第4页 / 共13页

007ts-1143201-16359647501073865723.pdf-第5页.png

第5页 / 共13页

007ts-1143201-16359647501073865723.pdf-第6页.png

第6页 / 共13页

007ts-1143201-16359647501073865723.pdf-第7页.png

第7页 / 共13页

007ts-1143201-16359647501073865723.pdf-第8页.png

第8页 / 共13页

非线性控制系统的反馈线性化尹逊和 1. 局部线性化—谐波线性化—全局线性化 1.1 局部线性化(Liapunov线性化，Jacobian线性化) 考虑下式所示的自治系统，假设是连续可微的，则 ( xf ) x = 系统的动态特性可以写为 ( xf ) x = ∂ ∂ f x ⎛ ⎜ ⎝ ⎞ ⎟ ⎠ x x = 0 (. toh+ f . x ) 令称系统 A = ∂ ∂ f x ⎛ ⎜ ⎝ ⎞ ⎟ ⎠ x 0= x = Ax 为原非线性系统在平衡点0处的线性化（或线性近似） 1

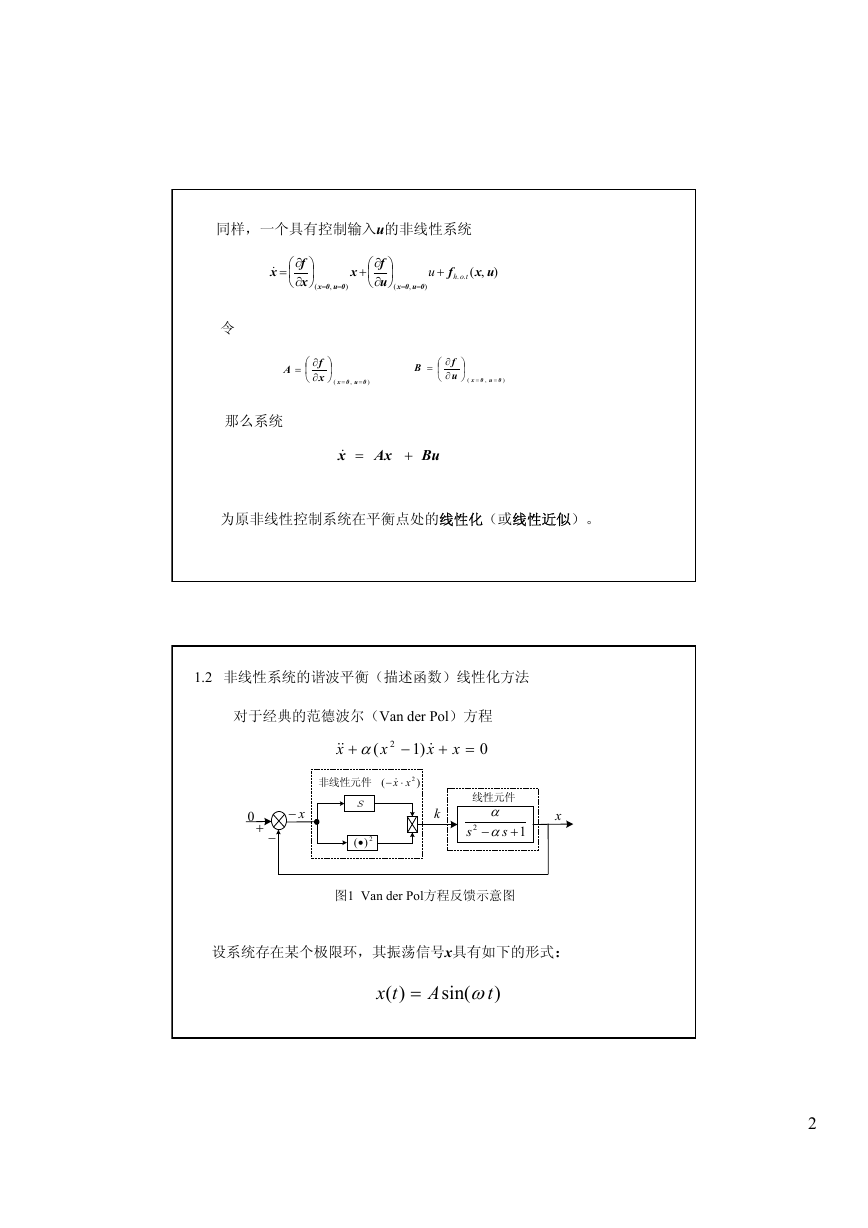
同样，一个具有控制输入u的非线性系统 x = f ∂ x ∂ ⎛ ⎜ ⎝ ⎞ ⎟ ⎠ ( 0u0x = = , ) x + f ∂ u ∂ ⎞ ⎟ ⎠ ⎛ ⎜ ⎝ ( 0u0x = = , ) u + f ,(. ux ) toh . 令 A = ∂ ∂ f x ⎛ ⎜ ⎝ ⎞ ⎟ ⎠ ( 那么系统 B = ∂ ∂ f u ⎛ ⎜ ⎝ ⎞ ⎟ ⎠ ( x = ) 0u0x = = , 0u0 = , ) = x Ax + Bu 为原非线性控制系统在平衡点处的线性化（或线性近似）。 1.2 非线性系统的谐波平衡（描述函数）线性化方法对于经典的范德波尔（Van der Pol）方程 α x ( + x 2 − )1 x + x = 0 非线性元件 ( 2xx ⋅− ) x− 0 + − s 2)(• k 线性元件 α − s s α 2 x + 1 图1 Van der Pol方程反馈示意图设系统存在某个极限环，其振荡信号x具有如下的形式： tx )( = A sin( t ω ) 2

非线性环节的输出为 k −= xx 2 −= A 3 ω 4 (cos( t ω ) − t 3 cos( ω )) 可以把k 近似为 k −≈ A 3 ω 4 cos( t ω ) = dA 2 dt 4 ⋅ [ − A sin( t ω )] 因此，可用图2所示的“拟线性”环节来近似图1所示的非线性环节。拟线性近似 k 2 A 4 s x− 0 + − 线性元件 α s α 2 − x s + 1 图2 非线性环节的拟线性近似我们定义非线性元件的描述函数为非线性元件输出的基波分量与输入正弦波的复数比，即 AN ( , ) ω = Me j ( φω 1 + t ) ( Ae j ω t ) = M A j φ 1 e = (1 A b 1 + ja ) 1 用描述函数表示非线性部分，当存在正弦输入时，非线性元件能被当作具有频率响应的线性元件处理 A ω t sin( ) 非线性元件 )(tω A ω sin( t ) ），（ ωAN M sin( 1φω +t ) 描述函数法的基本前提是假设系统具有很好的滤波性能；它是一种近似的方法，没有严格的数学基础，但在许多工程应用中是很有效的；它的最大的优点在于，可以利用已有的线性系统理论对非线性系统进行近似的分析和设计。 3

1.3 非线性系统的反馈（全局）线性化这种控制方法的基本思想是用代数变换将一个非线性系统的运动特性（全部或部分地）变换成线性的动态特性，从而可以用熟知的线性控制方法；这种方法1.1中提及的线性化完全不同，不同之处在于：反馈线性化是通过严格的状态变换和反馈达到的，而不是借助于动态特性的线性近似。反馈线性化方法可以看成是将原始的系统模型变换成形式较为简单的等效模型的方法。 2. 反馈线性化的直观概念 2.1 反馈线性化最简单形式的反馈线性化是将非线性系统中的非线性抵消掉，使闭环动态特性变成线性形式。 u 水箱的动态模型为 d dt h 0 ⎡∫ ⎢⎣ dhhA )( ⎤ =⎥⎦ tu )( − a 2 gh hd − 0h 输出流量水箱液面高度控制可重写为 = hhA )( tu )( − a 2 gh 4

若选 ( tu 为) tu )( = a 2 gh + hA υ)( 式中为待求的“等效输入”，则得到线性的动态方程 υ υ=h 若选 h~ αυ −= (1) (2) ~ h = 其中态方程为 th )( − dh 为液面高度误差，为一严格正实常数，则得到闭环动 α (3) ~ h α + h = )(~ →th 0 0 这说明，当由式(1)和(2)可知，实际的输入流量由下面的非线性控制律确定时，∞→t tu )( = a 2 gh ~)( h hA α− 由上式可以看出，右端第一项用来提供输出流量，第二项则是用来根据期望的线性动态特性(3)去改变液面的高度。 2.2 输入-状态线性化考虑单输入非线性系统 x = f x ,( u ) 中控制输入u的设计问题。输入-状态线性化的方法通过两步来解决这个问题: 首先，找出一个状态变换使非线性动态方程化成一个等效的线性定常系统的动态方程，并表示成熟知的形式。 (xz ) 与一个输入变换 u = ,( υxu ) z = 其次，再利用标准的线性控制方法（例如极点配置、最优控制等）来设计。υ 5

以简单的二阶系统为例来说明这个方法。 x x 1 2 x 2 −= x −= 2 + 1 cos ax x 2 1 + + x sin 1 u cos( 2 x 1 ) 考虑一组新的状态变量 x 1 ax = = z z 1 2 + sin x 1 2 则新的状态方程为 z z 1 2 z 2 −= xa = 2 z 2 −= z + 2 1 (cos + z cos 1 1 xx ) 1 1 cos + z 1 sin z 1 + au cos( z )2 1 下面的控制律 u = 1 cos( a z )2 1 ( − υ cos z 1 sin z 1 + 2 z 1 cos z 1 ) υ 可用来抵消上式中的非线性。其中是待设计的等效输入（等效的含义是确定了，u也就确定了，反之亦然）。于是可得到线性的输入和输出关系为 z 1 + z 2 z z 1 2 2 −= υ= 由于新的动态系统是线性的和能控的，采用熟知的线性状态反馈控制律 =υ zk 11 + zk 22 就能对极点进行任意配置。不失一般性，现在把它的两个极点配置在-2处，那么反馈控制律即为 22 z−=υ 得到的闭环动态系统是稳定的。用原来的状态和表示，与此控制律相应的原控制输入为 u = 1 cos( x )2 1 原来的状态x由z给出为 a ax 2 x 1 − cos x 1 sin x 1 + 2 x 1 cos x 1 ) + z 2 1 2 z z 1x 2( − 2 z 1 z 2 −= 2 −= 2x sin2 − x 1 x 2 = = z 1 z ( − sin z 1 /) a 2 由于和两者均收敛于零，故原来的状态x也收敛于零。 1z 2z 6

2.3 输入-输出线性化考虑下面系统的跟踪控制问题 = x y = u ) f h x ( , x ( ) 假定设计的目的是使输出跟踪期望轨迹 )(ty )(tyd ，同时保持所有状态有界。可以猜测：假如能够找到系统输出和控制输入u之间一个直接而 )(ty 简单的关系，则跟踪控制的困难就会大大降低。事实上，这个直观的想法构成了非线性控制系统设计中所谓输入-输出线性化方法的基础。考虑三阶系统 1 2 3 x x x y = = = = ( x 2 + )1 x 3 x + + 2 + x u 3 sin x 5 1 x 2 1 x 1 为了得到输出y与输入u之间的直接关系， y = x 1 = sin x 2 + ( x 2 + )1 x 3 = y = x ( 5 + 1 x f )( 1 x 3 + )(cos x ( + 2 x + 2 u )1 x 3 ) + ( x 2 + )1 x 2 1 + ( x 2 + )1 u 如果选择控制输入为下面的形式 u = 1 + 1 x 2 ( υ − f 1 ) 其中为待定的新输入，得到一个输出与新输入之间的简单二重积分关系 υ υ=y 7

利用线性控制方法很容易对这个二重积分关系设计跟踪控制器。定义跟踪误差为 e = =υ ty )( y d y d− t )( ,选取新的输入为 − ek 1 − ek 2 其中 k 1, k 2 为正常数，则闭环系统的跟踪误差满足 e + ek 2 + ek 1 = 0 它代表一个指数稳定的误差动态特性。上面这种首先产生一个线性的输入输出关系，然后再利用线性控制方法构造控制器的设计策略称为输入-输出线性化方法。如果我们需要将系统的输出微分r次才能得到y与u之间的显式关系，则称该系统的相对度（Relative degree）为r。可一严格的证明，任何n阶能控系统，对任一输出，最多只需微分n次就一定能使控制输入在表达式中出现，亦即。n r ≤ 3 数学工具和基本概念为了使前面的直观概念内容形式化并推广到一大类非线性系统,我们介绍一些数学工具及其基本概念。我们把矢量函数 R →:f n n R 称为上的一个矢量场。 nR 矢量场的平滑性：是指函数具有要求的任意阶连续偏导数。给定一个状态 x 的平滑的标量函数h(x)，h的梯度记为：h∇ ( xf ) 它是以 ( h ∇ ) i ∂= h ∂ x i ∇ h = h ∂ x∂ 为元素的一个行矢量。类似地，给定一个矢量场 ( xf ) ，其Jacobian矩阵记为： f∇ =∇ f f ∂ x ∂ 它是一个以 ( f ∇ ) ij ∂= f ∂ i x j 为元素的 nn × 矩阵。 8

资料库

非线性控制系统的反馈线性化.pdf

相关推荐

课程资源

热门标签

最新资料