简支梁模态参数测定与分析.pdf-资料库

weixin_38741966-12210795-201005-530.pdf-第1页.png

第1页 / 共7页

weixin_38741966-12210795-201005-530.pdf-第2页.png

第2页 / 共7页

weixin_38741966-12210795-201005-530.pdf-第3页.png

第3页 / 共7页

weixin_38741966-12210795-201005-530.pdf-第4页.png

第4页 / 共7页

weixin_38741966-12210795-201005-530.pdf-第5页.png

第5页 / 共7页

weixin_38741966-12210795-201005-530.pdf-第6页.png

第6页 / 共7页

weixin_38741966-12210795-201005-530.pdf-第7页.png

第7页 / 共7页

中国科技论文在线 http://www.paper.edu.cn 简支梁模态参数测定与分析刘伟，陈俊杰* （长安大学汽车学院，西安 710064）摘要：振动是工程结构中一种普遍现象，而对等截面简支梁的振动分析是对工程振动的一种常见工具。将简支梁简化为离散的多自由度模型，对其进行理论分析，再通过实验测试的方法，可以分别得到简支梁的固有频率和固有振型。两种方法分别得到的简支梁模态参数结果大致相同。分析相应系统的固有频率和固有振型等，可以有效的避免对工程结构造成最大破坏的共振现象，避免了共振。从分析典型的简支梁模态参数入手，为我们分析复杂机构的振动提供了参考方法。关键词：简支梁；振动；模态参数；固有频率；固有振型；中图分类号：TB123 The analysis and test study on the modal parameter of simply supported beam Liu Wei, Chen Junjie (Automobile Institute of Chang'an University,Xi'an 710064) Abstract: The vibration is a common phenomenon in engineering structures.And the vibration analysis of the simple supported beam with cross-section is a common tool about the vibration of engineering. This paper analyzes the simple supported beam and makes it the discreted MDOF model. Then through a method of the experiment test. It can get the natural frequency and the natural vibration type respectively.Two methods have roughly the same results of the modal parameter of the simple supported beam.Analyse the corresponding system of natural frequencies and natural vibration types.That can avoid the largest destructive resonance phenomenon to engineering structures effectively. That means avoid resonance.Start with the modal parameter of the typical of the simple supported beam, which offered a reference method to analyze the complex mechanism. Keywords: simple supported beam; vibration；modal parameter;the natural frequency; the natural vibration type 0 引言工程中所有的机械在运动(运转)过程中，常常伴随着振动。振动对工程机构使用造成一定的影响，一定程度缩短了工程机械的使用寿命。因此，研究振动工程是发展工业生产和国民经济的需要，这一学科以力学和数学为基础，以现代测试技术、计算机技术为手段，它面向工程实际,以振动学科的理论、知识和方法来解决工程中日趋复杂的各种动力学问题。简支梁是工程中常见的振动模型，研究并掌握其工程分析方法具有重要的实践意义。本文通过等截面简支梁系统进行研究，对其进行动力学分析，运用理论分析和实验测试的方法，找出该系统振动的固有频率、振幅和，揭示该系统在外激励下产生共振现象的可能性和范围，以避免对机构破坏最大的共振可能的发生，达到主动避振的目的，为复杂机构的振动分析提供一定的分析参考。作者简介：刘伟（1985-），男，硕士研究生，车辆工程专业，主要研究车辆结构动态分析与测试技术. E-mail: liuwei323kk@163.com - 1 -

中国科技论文在线 1 简支梁相关参数说明 http://www.paper.edu.cn 本文是以一等截面简支梁为研究对象，为研究其弯曲振动问题，忽略其轴向位移，并假设梁的横截面在振动过程中是始终保持与梁的轴向垂直的平面，其结构如图 1 所示。图 1 简支梁结构简图 Fig. 1 The structure diagram of simple supported beam 本文中研究的简支梁几何参数：长：L=1.00m，宽：B=0.05m，高：H=0.012m，简支梁密度： mKg / 2 简支梁多自由度理论分析 =ρ 8.7 × 10 3 3 ，材料弹性模量：E= E = 2.2 × 10 11 mN / 2 对简支梁进行分析，其简化模型见图 1。为使分析结果尽量接近真值，将简支梁平均分成 40 份，取每份的中心作为每份的质心，这样连续的简支梁就可以简化为多自由度振动系统模型。根据材料力学和振动理论可以建立 40 互相耦合的常微分方程，可以通过模态分析使方程解耦后求得振动系统的固有频率和主阵型。由材料力学知识可知单位集中力 P 作用下的挠度公式为； δ= Pbx EIL 6 （L2-b2-x2） (0≤x≤L - b) 由影响系数法建立起柔度矩阵为[δ],根据简化模型建立质量矩阵[M ]，然后根据 [ K ]=[ ] 1−δ 即可求出刚度矩阵[ K ]，将[ K ] 代入系统频率方程特征值和特征向量，即可得到其固有频率和固有振型。 − MpK 2 = 0 中，求解其利用Ｍatlab 求解。求得前三阶固有频率为：28Hz，113Hz，254Hz。各阶固有频率之比 23 : …。求得前三阶固有振型相应点振幅数据见表 1 至表 3。 22 : 3f : …=1: 2f : 满足： 1f : Tab.1 The amplitude of the corresponding points of the first natural vibration type(cm) 表 1 第一阶固有振型相应点振幅（cm） 0.0088 0.0263 0.0436 0.0607 0.0774 0.0936 0.1093 0.1242 0.1384 0.1518 0.1642 0.1756 0.1859 0.1951 0.2031 0.2098 0.2152 0.2193 0.2221 0.2234 0.2234 0.2221 0.2193 0.2152 0.2098 0.2031 0.1951 0.1859 0.1756 0.1642 0.1518 0.1384 0.1242 0.1093 0.0936 0.0774 0.0607 0.0436 0.0263 0.0088 - 2 -

中国科技论文在线 http://www.paper.edu.cn 0.0175 Tab.2 The amplitude of the corresponding points of the second natural vibration type(cm) 0.0522 0.2174 0.1452 0.1907 0.0856 0.1168 0.1700 0.2066 0.2229 表 2 第二阶固有振型相应点振幅（cm） 0.2229 0.2174 0.2066 0.1907 0.1700 0.1452 0.1168 0.0856 0.0522 0.0175 -0.0175 -0.0522 -0.0856 -0.1168 -0.1452 -0.1700 -0.1907 -0.2066 -0.2174 -0.2229 -0.2229 -0.2174 -0.2066 -0.1907 -0.1700 -0.1452 -0.1168 -0.0856 -0.0522 -0.0175 Tab.3 The amplitude of the corresponding points of the third natural vibration type(cm) 表 3 第三阶固有振型相应点振幅（cm） 0.0263 0.0774 0.1242 0.1642 0.1951 0.2152 0.2234 0.2193 0.2031 0.1756 0.1384 0.0936 0.0436 -0.0088 -0.0607 -0.1093 -0.1518 -0.1859 -0.2098 -0.2221 -0.2221 -0.2098 -0.1859 -0.1518 -0.1093 -0.0607 -0.0088 0.0436 0.0936 0.1384 0.1756 0.2031 0.2193 0.2234 0.2152 0.1951 0.1642 0.1242 0.0774 0.0263 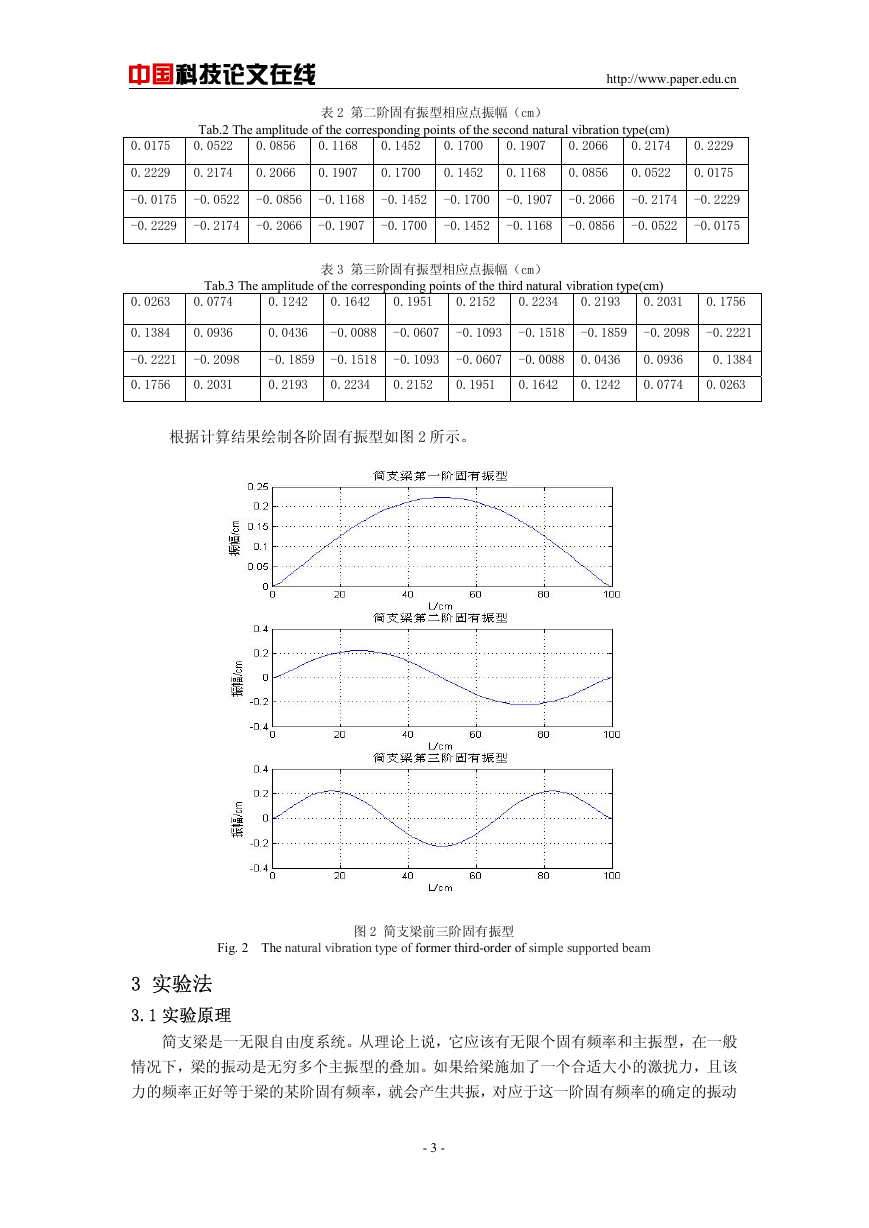根据计算结果绘制各阶固有振型如图 2 所示。 Fig. 2 The natural vibration type of former third-order of simple supported beam 图 2 简支梁前三阶固有振型 3 实验法 3.1 实验原理简支梁是一无限自由度系统。从理论上说，它应该有无限个固有频率和主振型，在一般情况下，梁的振动是无穷多个主振型的叠加。如果给梁施加了一个合适大小的激扰力，且该力的频率正好等于梁的某阶固有频率，就会产生共振，对应于这一阶固有频率的确定的振动 - 3 -

中国科技论文在线 http://www.paper.edu.cn 形态叫做这一阶的主振型，这时其他各阶振型的影响小得可以忽略不计。首先通过扫频法找到梁各阶的固有频率，然后让激振力频率等于各阶固有频率，使梁产生共振，然后，测定共振状态下梁上各测点的振动加速度值。本实验所用的简支梁是在小阻尼状态下进行理论分析的，忽略小阻尼的影响后，简支梁上各点基本上同时达到最大或者最小值，这个过程可以从实验仪器中的相位信息读出来。两节点之间上的测点的相位基本上相同，节点异测各测点相位基本相差π。由于采用的是正弦激励，故可知输出为 Y=Asin(wt+ϕ); Y’=w Acos(wt+ϕ); Y’’=-w2Asin(wt+ϕ); Y 1 Y 2 '' '' = A 1 A 2 ；其中 Y 是简支梁上测点的位移；Y’为速度；Y’’为加速度；w 为振动的固有频率；由此得出简支梁上各个测点之间振幅之比等于各个测点的加速度之比；故简支梁的振型可以用加速度的比值做出，此方法称为归一化。 3.2 实验方法依据简支梁固有频率和振型实验求解方法，利用正弦信号发生器产生信号，通过功率放大器将信号放大，控制电磁激振器对简支梁产生相应激励。在简支梁相应位置利用加速度信号传感器采集到信号，通过电荷放大器对信号进行合适倍数放大，再输入到 Synergy 信号采集分析仪进行分析处理。实验装置如图 3 所示。图 3 实验装置图 Fig.3 The experimental device 3.3 固有频率测量简支梁具有无限阶固有频率和振型，相应固有频率满足一定比例关系，在此只考虑简支梁前三阶固有频率和振型。根据理论分析所得数据，在实验中，先调节正弦信号发生器从 5Hz 到 300Hz 进行扫频，加速度传感器放在简支梁非节点处。当激励频率与简支梁固有频率接近时，简支梁振幅增大，同时由于振动加强发出声音，激励达到简支梁固有频率，将产生共振，此时振幅最大。扫频完成，将接受到加速度传感器信号利用 Synergy 信号采集分析仪 - 4 -

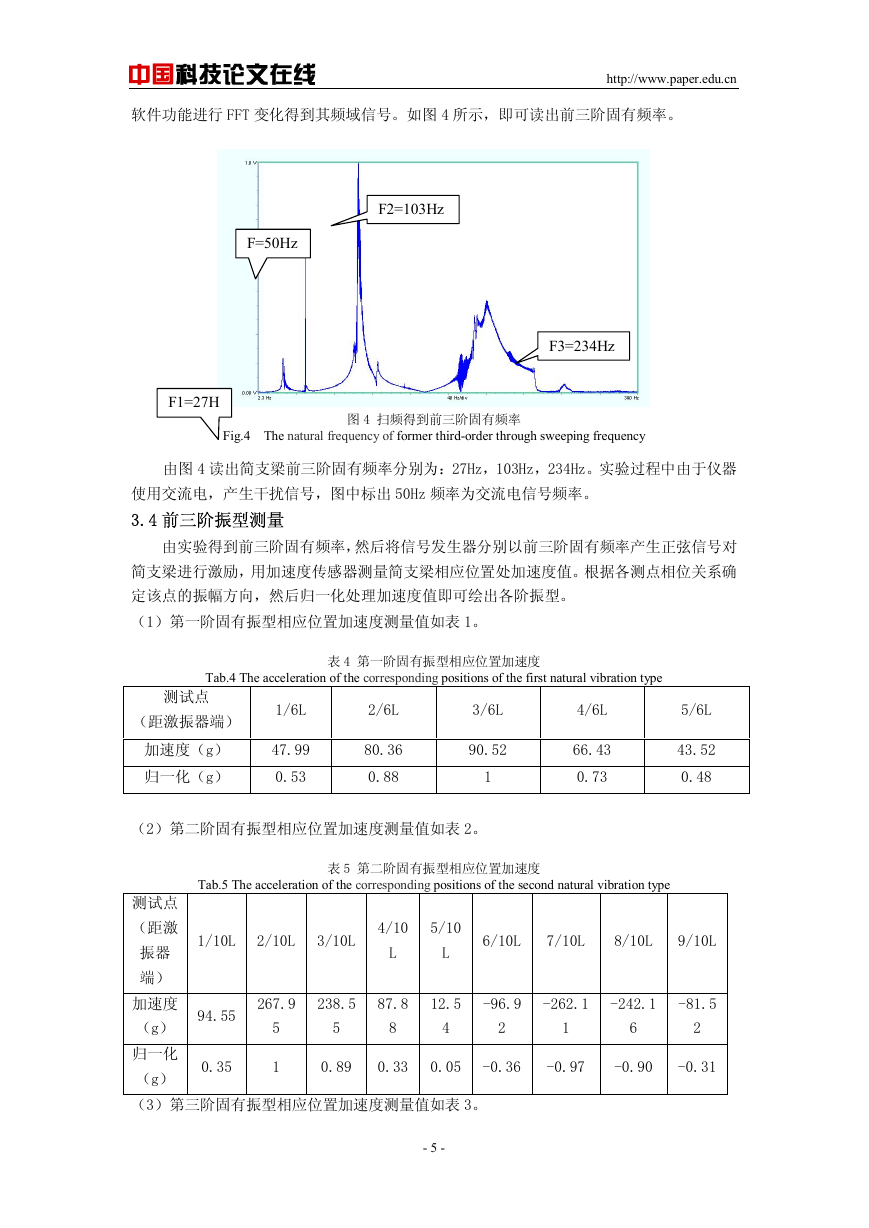
中国科技论文在线 http://www.paper.edu.cn 软件功能进行 FFT 变化得到其频域信号。如图 4 所示，即可读出前三阶固有频率。 F2=103Hz F=50Hz F1=27H F3=234Hz Fig.4 The natural frequency of former third-order through sweeping frequency 图 4 扫频得到前三阶固有频率由图 4 读出简支梁前三阶固有频率分别为：27Hz，103Hz，234Hz。实验过程中由于仪器使用交流电，产生干扰信号，图中标出 50Hz 频率为交流电信号频率。 3.4 前三阶振型测量由实验得到前三阶固有频率，然后将信号发生器分别以前三阶固有频率产生正弦信号对简支梁进行激励，用加速度传感器测量简支梁相应位置处加速度值。根据各测点相位关系确定该点的振幅方向，然后归一化处理加速度值即可绘出各阶振型。（1）第一阶固有振型相应位置加速度测量值如表 1。 Tab.4 The acceleration of the corresponding positions of the first natural vibration type 表 4 第一阶固有振型相应位置加速度测试点（距激振器端） 1/6L 2/6L 3/6L 4/6L 5/6L 加速度（g） 47.99 归一化（g） 0.53 80.36 0.88 90.52 1 66.43 0.73 43.52 0.48 （2）第二阶固有振型相应位置加速度测量值如表 2。 Tab.5 The acceleration of the corresponding positions of the second natural vibration type 表 5 第二阶固有振型相应位置加速度测试点（距激振器端）加速度（g）归一化（g） 1/10L 2/10L 3/10L 4/10 5/10 L L 6/10L 7/10L 8/10L 9/10L 94.55 0.35 267.9 238.5 87.8 12.5 -96.9 -262.1 -242.1 -81.5 5 1 5 8 4 2 1 6 2 0.89 0.33 0.05 -0.36 -0.97 -0.90 -0.31 （3）第三阶固有振型相应位置加速度测量值如表 3。 - 5 -

中国科技论文在线 http://www.paper.edu.cn Tab.6 The acceleration of the corresponding positions of the third natural vibration type 表 6 第三阶固有振型相应位置加速度测试点（距激振 1/13L 2/13L 3/13L 4/13L 5/13L 6/13L 器端）加速度（g） 114.33 128.08 82.54 43.26 -63.51 -118.35 归一化（g） 0.89 1 0.65 0.34 -50 -0.92 测试点（距激振 7/13L 8/13L 9/13L 10/13L 11/13L 12/13L 器端）加速度（g） -99.67 -57.36 38.47 74.35 108.34 62.35 归一化（g） -0.78 -0.48 0.30 0.58 0.85 0.48 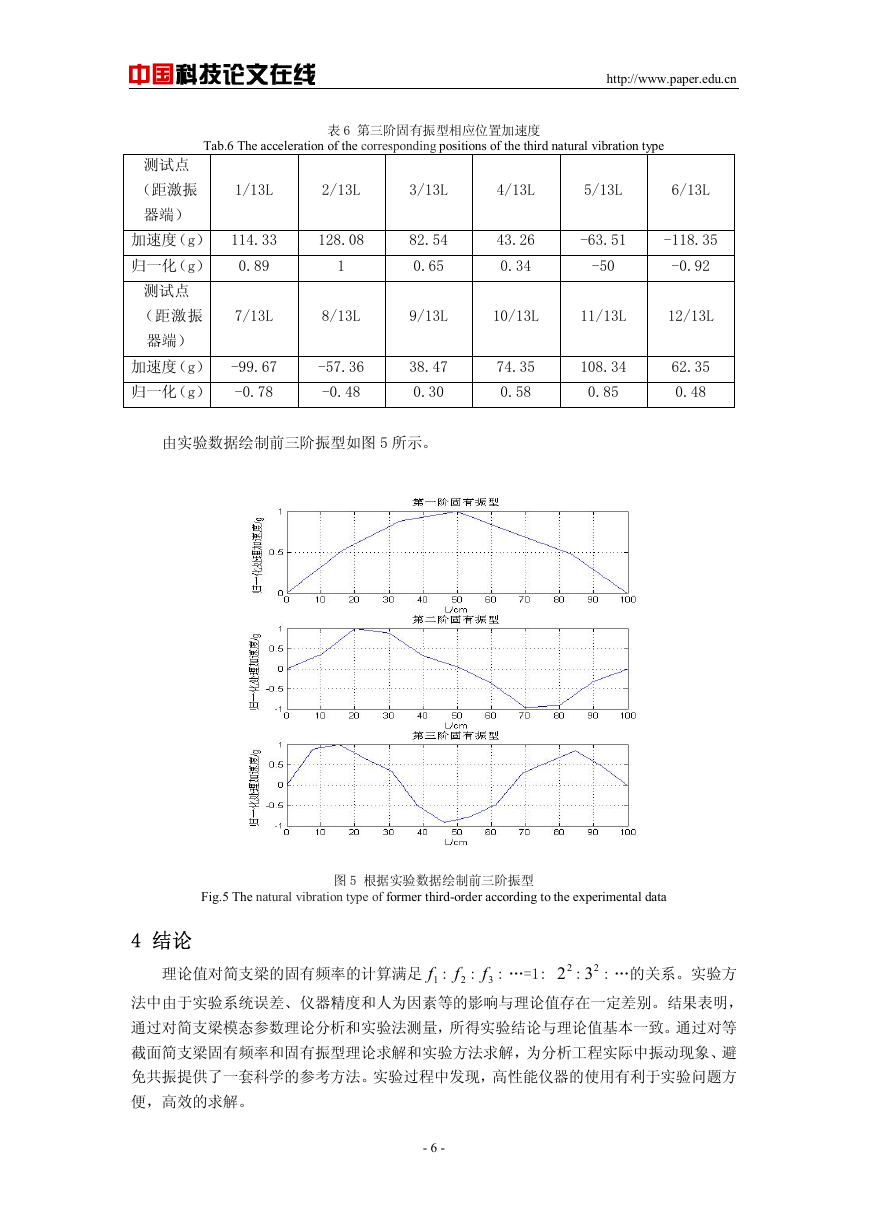由实验数据绘制前三阶振型如图 5 所示。 Fig.5 The natural vibration type of former third-order according to the experimental data 图 5 根据实验数据绘制前三阶振型 4 结论理论值对简支梁的固有频率的计算满足 1f : 2f : 3f : …=1: 22 : 23 : …的关系。实验方法中由于实验系统误差、仪器精度和人为因素等的影响与理论值存在一定差别。结果表明，通过对简支梁模态参数理论分析和实验法测量，所得实验结论与理论值基本一致。通过对等截面简支梁固有频率和固有振型理论求解和实验方法求解，为分析工程实际中振动现象、避免共振提供了一套科学的参考方法。实验过程中发现，高性能仪器的使用有利于实验问题方便，高效的求解。 - 6 -

中国科技论文在线 [参考文献] (References) http://www.paper.edu.cn [1] 刘习军，贾启芬.工程振动理论与测试技术[M].北京:高等教育出版社,2004. [2] 诸德超等.工程振动基础 [M].北京:北京航空航天出版社,2004. [3] 李伟民，何伟，杨琳. 简支梁振动特性的理论分析及实验研究[J].贵州教育学院学报(自然科学),2007(4):44-49. [4] 文涛，胡青春.基于 MATLAB 语言的多自由度振动系统的固有频率及主振型计算分析[J].中国制造业信息化,2007(1):78-81. [5] 戴丽玲. 简支梁固有频率与固有振型的实验室测量与理论分析[J].昆明学院学报,2008,30(4):86-89. [6] 梁虹，梁洁，陈跃斌.信号与系统分析及 MATLAB 实现[M].北京：电子工业出版社,2002

资料库

简支梁模态参数测定与分析.pdf

相关推荐

开发技术

热门标签

最新资料