logo资料库

带攻击角度约束的非奇异终端滑模固定时间收敛制导律.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.48M 资料格式：pdf 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    带攻击角度约束的非奇异终端滑模固定时间收敛制导律 李晓宝, 张友安, 鲍虎, 赵国荣 引用本文: 李晓宝, 张友安, 鲍虎, 等. 带攻击角度约束的非奇异终端滑模固定时间收敛制导律[J]. 控制与决策, 2020, 35(2): 474-482. 在线阅读 View online: https://doi.org/10.13195/j.kzyjc.2018.0443 您可能感兴趣的其他文章 Articles you may be interested in 带有非匹配扰动的连铸结晶器振动位移系统自适应反步滑模控制 Adaptive backstepping sliding mode control for oscillation displacement system of continuous casting mold with unmatched perturbations 控制与决策. 2020, 35(3): 578-586 https://doi.org/10.13195/j.kzyjc.2018.0761 基于混合滑模控制器和反正切观测器的SPMSM直接转矩控制 Direct torque control of SPMSM based on hybrid sliding mode controller and arctangent observer 控制与决策. 2019, 34(9): 1831-1839 https://doi.org/10.13195/j.kzyjc.2018.1624 带有摩擦非线性的CMG框架伺服系统有限时间自适应鲁棒控制 Finite-time adaptive robust control for CMG gimbal servo system with friction nonlinearities 控制与决策. 2019, 34(4): 885-890 https://doi.org/10.13195/j.kzyjc.2017.1296 一种基于时变干扰观测器的高超声速飞行器容错控制策略设计 A FTC scheme for hypersonic vehicle based on adaptive disturbance observer 控制与决策. 2018, 33(10): 1893-1900 https://doi.org/10.13195/j.kzyjc.2017.0645 输入受限约束下的无抖振有限时间稳定趋近律设计 Finite time stable chattering-free reaching law design with bounded input 控制与决策. 2018, 33(1): 135-142 https://doi.org/10.13195/j.kzyjc.2016.1427 欠驱动飞艇平面路径跟踪控制 Planar path-following control for an under-actuated airship 控制与决策. 2017, 32(6): 983-988 https://doi.org/10.13195/j.kzyjc.2016.0464 基于一种新型趋近律的自适应滑模控制 Adaptive sliding control based on a new reaching law 控制与决策. 2016, 31(7): 1335-1338 https://doi.org/10.13195/j.kzyjc.2015.0518 多输入不确定系统的平滑非奇异终端滑模控制 Smooth nonsingular terminal sliding mode control of uncertain multi-input systems 控制与决策. 2015(1): 161-165 https://doi.org/10.13195/j.kzyjc.2013.1370
    第 35 卷 第 2 期 2020 年 2月 控 制 与 决 策 and Decision Control Vol.35 No.2 Feb. 2020 文章编号: 1001-0920(2020)02-0474-09 DOI: 10.13195/j.kzyjc.2018.0443 带攻击角度约束的非奇异终端滑模固定时间收敛制导律 李晓宝1y, 张友安2, 鲍 虎3, 赵国荣4 (1. 海军航空大学 航空基础学院，烟台 264001；2. 烟台南山学院 电气与电子工程系，烟台 265713； 3. 烟台南山学院 航空学院，烟台 265713；4. 海军航空大学 参谋部，烟台 264001) 文献标志码: A 摘 要: 针对拦截机动目标的末制导问题, 设计一种带攻击角度约束的末制导律. 该制导律构造一种新型的固定 时间收敛非奇异终端滑模面, 能够在解决终端滑模面奇异性问题的同时使得滑模面、弹目视线角和弹目视线角 速率在固定时间内收敛, 保证收敛时间的上界是独立于弹目初始条件, 可以被预先设定的. 与传统的固定时间收 敛控制相比, 该制导律通过调节滑膜面和弹目视线角误差的趋近律指数使得制导系统收敛速率更快. 同时, 针对 目标机动引起的未知扰动, 引入一种扩张状态观测器进行估计, 能够增强制导系统的鲁棒性, 避免震颤现象的发 生. 最后, 通过仿真实验验证所提出制导律能够以不同的攻击角度对机动目标进行有效拦截, 且与其他制导律相 比, 所提出的制导律使得制导系统收敛更快, 导弹拦截时间更短, 拦截精度更高. 关键词: 制导律；攻击角度约束；非奇异终端滑模；固定时间收敛；扩张状态观测器；机动目标 中图分类号: V448.133 Nonsingular terminal sliding mode based impact angle constraint guidance law with fixed-time convergence LI Xiao-bao1y, ZHANG You-an2, BAO Hu3, ZHAO Guo-rong4 (1. School of Coast Defence，Naval Aviation University，Yantai 264001，China；2. Department of Electrical and Electronic Engineering，Yantai Nanshan University，Yantai 265713，China；3. Aviation Academy, Yantai Nanshan University，Yantai 265713，China；4. University Staff，Naval Aviation University，Yantai 264001，China) Abstract: A terfminal guidance law is developed for missiles intercepting maneuvering targets with impact angle constraints. A novel nonsingular terminal sliding mode with fixed-time convergence is constructed to avoid the singularity problem while ensuring the sliding surface, LOS angle and the LOS angular rate are fixed-time convergent. The upper-bound of convergence time is independent of the initial states of missiles and targets and can be set in advance. Compared with conventional fixed-time convergence control, the proposed guidance law has a faster convergence rate by regulating the index of the approaching laws of the sliding surface and the LOS angle error. Besides, an extended state observer is introduced to estimate the unknown disturbance caused by the target acceleration, which ensures that the guidance system has a good robustness and avoids the chattering problem. Finally, simulation results indicate that with the proposed guidance law, the missile can intercept the maneuvering targets effectively under different impact angles. Besides, comparisons with other guidance laws show that the proposed guidance law can improve the convergence rate of the guidance system and allow the missie to intercept the targets more accurately in less time. Keywords: guidance law；impact angle constraint；nonsingular terminal sliding mode；fixed-time convergence； extended state observer；maneuvering target 0 引 使用精确制导武器对目标实施精确快速拦截 是现在和未来战争中的主要作战方式. 导弹末制导 律的设计不仅要求导弹以较小的脱靶量击中目标, 还需要导弹以特定的攻击角度命中目标以求对作 战目标最大的毁伤效果. 比例导引律由于其简单高 效的特点被广泛地应用于拦截静止或缓慢移动的目 标[1-2]. 然而, 随着目标机动能力的提升, 比例导引律 的制导效果变得不尽人意[3], 为了有效地处理机动目 标, 实现对机动目标的精确拦截, 近些年现代控制理 论已经被广泛应用到导弹制导律的设计中,如最优控 制制导律[4]、微分对策制导律[5]、控制制导律[6] 以及 收稿日期: 2018-04-11；修回日期: 2018-09-05. 基金项目: 国家自然科学基金项目(61273058). 责任编委: 刘允刚. y 通讯作者. E-mail: lixiaobaohjhy@163.com.
    第2期 李晓宝 等: 带攻击角度约束的非奇异终端滑模固定时间收敛制导律 475 滑模控制制导律[7]. 传统的滑模控制通常采用线性滑模面使系统状 态渐近收敛到平衡点上, 但其收敛时间是趋于无穷 的[8]. 现代战争中高速飞行的导弹在打击目标时, 留 给末制导的时间往往只有短短几十秒钟,这就迫切要 求弹目视线(line of sight, LOS) 角速率能够快速收敛, 以保证导弹在与目标撞击之前稳定到期望的LOS 角 方向, 提高制导性能. 终端滑模控制(terminal sliding mode control, TSMC) 通 过 引 入 非 线 性 滑 模 面 确 保 了系统状态能够在有限时间内收敛[9]. 近年来, 采用 TSMC 方法针对机动目标进行制导律的设计得到了 广泛的研究[10-15], 然而 TSMC 方法存在奇异性问题. 为此, 文献 [11] 提出了转换滑模面的方法, 文献 [12] 在研究一类非线性系统过程中给出了非奇异终端滑 模控制方法, 文献[13] 在研究带攻击角度约束的制导 律中设计了一种积分滑模面来避免奇异问题. 此外, 当系统状态远离平衡点时, TSMC 收敛速率较慢, 为 了加快收敛速率, 文献[14-15] 提出了非奇异快速终 端滑模控制方法. 采用有限时间收敛 TSMC 得到的 系统状态收敛时间依赖于系统的初始条件. 在设计 导弹的制导律过程中, 导弹和目标的具体初始状态 通常是事先未知的,不同的初始条件得到的收敛时间 也不同. 作为有限时间稳定性理论的扩展, 文献[16] 在研究一类非线性系统过程中提出了固定时间收 敛 (fixed-time convergence, FTC) 的概念, FTC 理论可 以使系统得到一个独立于初始条件的收敛时间上界. 采用 FTC 进行制导律设计时, 可以将系统状态 的收敛时间上界通过参数控制预先设定为不依赖于 初始条件的固定值, 从而使得设计的制导律适用范 围更广, 制导性能更高. 为此, 本文将固定时间收敛应 用于制导律设计中, 提出一种带有攻击角度约束的 非奇异终端滑模固定时间收敛制导律设计方法. 该 方法在解决终端滑模面奇异性问题的同时, 使得滑 模面、LOS 角以及LOS 角速率能够在固定时间内快 速收敛. 与传统的固定时间收敛控制方法相比, 该制 导律具有更快的收敛速率. 此外, 针对目标机动引起 的扰动,本文设计一种扩张状态观测器来对其进行估 计. 最后, 通过仿真验证该制导律的可行性并与其他 制导律对比,对该制导律的制导性能进行分析. 1 问题和相关引理 1.1 问题描述 考虑二维平面内的导弹末制导问题, 如图 1 所 示. 假定导弹 M 和目标 Y 的速度是恒定的, 记为 VM 和 VT ; r 和 q 分别表示弹目距离和LOS 角; M 和 T 分 别表示导弹和目标的航迹角; aM 和 aT 分别表示导弹 和目标的法向加速度. 图 1 二维平面内的弹目运动关系 制导系统的运动学方程可以表示为 _r = VT cos(rT q) VMcos(M q); _q = 1 r _M = [VT sin(T q) VMsin(M q)]; aM VM aT VT _T = ; : (1) 对方程组 (1) 中 LOS 角速率 _q 求解关于时间 t 的 一阶导数可以得到 q = _r r2 [VT sin(T q) VM sin(M [VT ( _T _q)cos(T q) q)] + 1 r 1 r r2 (r _q) + VM ( _M _q)cos(M q)] = _r [ _qVT cos(T q)+ _qVMcos(M q) + VT _T cos(T q) VM _Mcos(M q)] = _r _q r aMcos(M q) aT cos(T q) _q _ r aT cos(T q) + + = r + 2 _r _q r r r aMcos(M q) r : (2) 导弹末制导终端攻击角度 表示为导弹击中目 标时二者速度之间的夹角, 该角度与终端 LOS 角 qf 存在着一一对应关系,即 ( ) qf = T f tan1 sin cosVT /VM : (3) 因此, 导弹末制导终端攻击角度 约束可以转化为终 端LOS角qf 约束的问题[17]. 假设 qd 是期望的末制导终端LOS 角, 定义 x1 = q qd 为LOS 角跟踪误差, x2 = _q 为LOS 角速率. 由 式(1)和(2)可得 _x1 = x2; oXYMraMVMaTVTTqγMγT
    476 控 制 与 决 策 _x2 = 2 _rx2 r cos(M q) r 其中d = cos(T q)aT . aM + d r ; (4) 假设1 理想状态下仅考虑目标机动 aT 对制导 系统的影响, 式(4) 中的 d 可以看作是目标机动引起 的外部干扰, 假设 ∆ 是一个正常数, 表示为目标机动 aT 的最大值,则jdj ⩽ ∆. 本文的目的是通过合理地设计导弹加速度指令 aM,使得LOS角跟踪误差 x1 和LOS角速率 x2 在固定 时间内收敛到原点的一个充分小的邻域内,以确保导 弹能够以期望的攻击角度击中目标. 1.2 基本定理 定义1 [16] 考虑如下非线性系统: _x(t) = F (x; t); x(0) = x0: (5) 其中: x 2 Rn; F (x; t) : U R+ ! Rn 是连续的, U 是包含 x = 0 的一个开区间, 且满足 F (0; t) = 0. 如 果对于任意给定的初始时间t0 和初始状态xt 2 U,都 存在一个时刻 T (x0), 使得系统(5) 的每一个解 x(t) = x(t; t0; x0)满足 = x(t; t0; x0) = 0; t 2 [t0; T (x0)); t!T (x0) x(t; t0; x0) = 0; t ⩾ T (x0); (6) 8><>: lim 则系统(5) 的平衡点 x = 0 是有限时间稳定的. 此外, 如果收敛时间 T (x0) 是有界的, 即对于任意的 x0 2 Rn, 存在 Tmin > 0, 使得 T (x0) < Tmin, 则系统(5) 的 平衡点x = 0被称作是固定时间稳定的. 引理1 [18] 考虑如下一类系统: _y = l1signm1y l2signm2y; y(0) = y0: (7) 其中: signmy = jyjmsign(y); l1 > 0; l2 > 0; m1 > 1; 0 < m2 < 1. 则系统(7) 的平衡点是固定时间稳定 的,且收敛时间T 是有界的,并满足 1 1 + T < Tmax = l1(m1 1) 引理2 考虑如下一类系统: _y = l1sign1y l2sgin2y; y(0) = y0: l2(1 m2) : (8) (9) 其中 1 = 2 = 1 + m1 2 1 + m2 2 + + m1 1 1 m2 2 2 sign(jyj 1); sign(jyj 1); l1 > 0; l2 > 0; m1 > 1; 0 < m2 < 1: 则系统(9) 的平衡点是固定时间稳定的, 且收敛时间 T 是有界的,并满足 令 则 即 第35卷 : 1 1 + ln 1 + 1 + l2 l1 ) ) l1 l2 (10) l1(1 m2) 证明 系统(9)可以写成 T ⩽ Tmax = ln l2(m1 1) ( ( 8<: _y = l1signm1y l2y; jyj > 1; 8<: _z = l1e(m11)(z1) l2; z > 1; _y = l1y l2signm2y; jyj ⩽ 1: (11) 当jyj > 1 时, 令 z = 1 + lnjyj; 当jyj ⩽ 1 时, 令 z = jyj1m2, 且 z0 为 y 取 y(0) 时对应的初值, 则上式 _z = (1 m2)l1z (1 m2)l2; 0 < z ⩽ 1: 可以转化为 由式(12)可得系统(9)收敛时间上界Tmax 为 (12) Tmax = lim y(0)!+1 T (y(0)) = lim z0 1 (w w w 0 1 z0 1 1 z0!+1 1 m2 lim z0!+1 1 l1(1 m2) 1 ) 1 ) l1e(m11)(z1) + l2 1 dz = l1z + l2 ( l1 + l2 l1e(m11)(z1) + l2 ln w l2 : 1 dz+ dz+ z0 T1 = lim z0!+1 = e(m11)(z1); 1 l1e(m11)(z1) + l2 dz; w w ( lim 0!+1 lim 0!+1 T1 = 1 m1 1 m1 1 l2(m1 1) 1 1 ln l1 + l2 l1 ) d = l1 l2(l1 + l2) (l1 + l2) ( 0 1 1 0 1 + 1 l2 ) ; d = ( ( ln ln 1 + 1 + ) ) + : □ l2 l1 l1 l2 Tmax = 1 l2(m1 1) l1(1 m2) 1 注1 文献[17]给出了一个固定时间收敛系统 _y = 0signy 0signp1/q1y; 并求出收敛时间上界
    李晓宝 等: 带攻击角度约束的非奇异终端滑模固定时间收敛制导律 477 signm2x1; " < jx1j ⩽ 1; 1sign1(x1) + 2sign2(x1); jx1j ⩽ "; 第2期 T < ( ) : q1 n1 0 0 + 1 + 0(m1 n1) n1 + m1 ln sign(jyj 1); 0 > 其中: = ) 0; 0 > 0; m1、n1、p1、q1 是正奇数, 并且满足 m1 > n1; p1 < q1. 因为 l2 l1 0(q1 p1) m1 n1 ( ⩽ l2 l1 ⩽ l1 l2 ( ) l1 l2 2n1 2n1 1 + 1 + ln ln ; + ; 所以本文设计的固定时间收敛系统相较于文献[17] 和文献[18],具有更快的收敛速率. 2 带有攻击角度约束的非奇异终端滑模固 定时间收敛制导律设计 2.1 固定时间收敛非奇异终端滑模面构造 考虑二阶非线性系统 (4), 文献 [19] 给出了一种 固定时间收敛的终端滑模面的一般设计如下: s = x2 + l1signm1x1 + l2signm2x1: (13) 其中: l1 > 0; l2 > 0; m1 > 1; 0 < m2 < 1. 基于滑模 面(13)的控制输入aM 被设计为 r 2 _rx2 r aM = cos(M q) l2m2jx1jm21x2 + k1sign1s+ k2sign2s + signs ) : ( k3 r + l1m1jx1jm11x2+ (14) 其中: 1 > 0; 0 < 2 < 1; k1 > 0; k2 > 0; k3 = ∆. 然 而, 式(14) 中, 当 x1 = 0; x2 ̸= 0 时, 幂次项jx1jm21x2 可能会引起奇异问题. 为了避免奇异现象的出现, 文 献[20] 提出了一种新型的非奇异终端滑模面设计方 法如下: (15) 其中: l > 0. g(x1) 2 R 定义为 s = x2 + l1x1 + l2g(x1): 8<:signm2x1; jx1j > "; 1x1 + 2sign(x1)x2 g(x1) = 1; jx1j ⩽ ": 1 = (2 m2)"m21; 2 = (m2 1)"m22: 0 < m2 < 1; "是一个小的正常数. 受文献 [20] 的启发, 本文提出一种新型的固定 时间收敛非奇异终端滑模面 (fixed-time convergence nonsingular terminal sliding mode, FTCNTSM)如下: s = x2 + l1sign1x1 + l2g(x1): 其中g(x1) 2 R 定义如下: (16) 8>>><>>>:x1; jx1j > 1; 2 m2 2 1 m2 1 2 1 "m21; "m22; g(x1) = 1 = _g(x1) =8>>><>>>:x2; jx1j > 1; 2 = 1; 2 ⩾ 1 且 1 ̸= 2; " 是一个小于 1 的正常数. 则 g(x1)的导数为 m2jx1jm21x2; " < jx1j ⩽ 1; 11jx1j11x2 + 22jx1j21x2; jx1j ⩽ ": 本文提出的固定时间收敛非奇异终端滑模面 s 及其导数 _s 都是连续的, 当jx1j > " 时, 式(16) 与系统 (9) 相似; 当jx1j ⩽ " 时, 式(16) 中的幂次项 l2signm2x1 被 1sign1(x1) + 2sign2(x1) 代替, 由于 1; 2 > 1, 避免了奇异问题的发生. 相较于文献 [19], 本文给出 了带有signm2x1 项滑模面解决奇异性问题的一般性 设计,并将有限时间收敛滑模面扩展到固定时间收敛 滑模面. 相较于文献 [17] 和文献 [18], 合理地设计制 导律可使得滑模面在到达阶段和滑动阶段具有更快 的收敛速率. 2.2 制导律设计 定理1 对于制导系统(4) 采用FTCNTSM 设计 方法,如果制导指令M 设计为 r aM = cos(M q) l2 _g(x) + k1sign3s + k3sign4s + 2 _rx2 r + l11jx1j11x2+ ) sign(s) : (17) k3 r ( 其中 3 = 4 = 1 + 1 2 1 + 2 2 + + 1 1 1 2 2 2 sign(jsj 1); sign(jsj 1): 则滑模面 s 将在时间 T 内收敛到 0, 状态量 x = [x1; x2]T 将在时间 T 内收敛到区域 D = fx1; x2jjx1j < 1;jx2j < 2g. 这里 ( ( ( 1 + 1 + ) ) ) k2 k1 k1 k2 l2 l1 + ; l + + T1 = T2 = 1 1 k2(1 1) k1(1 2) l2(m1 1) 1 ln ln ln
    控 制 与 决 策 478 ) ( 1 + l1 l2 1 l1(1 m2) ln < T1; T < T1 + T2; ′ T 1 = "; 2 = l1" + l2"m2: 证明 考虑如下Lyapunov函数: V = S2: ; 根据式(16) 和(17), Lyapunov 函数 V 的导数可以写为 如下形式: _V = 2s _s = 2s( _x2 + l11jx1j11x2 + l2 _g(x1)) ⩽ 2s(k1sign3s + k2sign4s) = 2k1V 2 2k2V 3+1 4+1 2 : (18) 由式 (18) 以及引理 2 可知, 系统 FTCNTSM 可在 内收敛到 s = 0. 当 s = 0 时, 分两种情 固定时间 T 况进一步讨论制导系统(4)的状态x1、x2 的变化情况. ′ 情况1 如果jx1j > ",由FTCNTSM可得 s = x2 + l1sign1x1 + l2sign2x1 = 0: (19) 1, 由式 (4) 和 (19) 可得 选取 Lyapunov 函数 V1 = x2 Lyapunov函数V1 的导数为 _V1 = 2x1 _x = 2x1(l1sign1x1 + l2sign2x1) = 2l1V 2l2V 2+1 1+1 2 2 1 1 : (20) 由式(20) 以及引理2 可知, 制导系统(4) 的状态量 x1 将在固定时间 T 内收敛到区域jx1j < 1 = ". 此 时,由式(19)可得 jx2j = jl1x1 + l2signm2xj ⩽ l1" + l2"m2: (21) 即制导系统 (4) 的状态量 x2 将在固定时间 T 内收敛 到区域jx2j < 2 = l1" + l2"m2. 情况2 如果jx1j ⩽ ",由FTCNTSM可得 s = x2 + l1x1 + l2(1sign1(x1) + 2sign2(x1)) = 0: (22) 由式(22)可以得到 jx2j = jl1x1 + l2(1sign1(x1) + 2sign2(x1))j ⩽ l1" + l2(1"1 + 2"2) = (23) l1" + l2"m2: 同样地, 制导系统 (4) 的状态量 x = [x1; x2]T 将 第35卷 2jg.2 在时间 T 内收敛到区域 D = fx1; x2jjx1j < 1;jx2 < 注2 由定理 1 可知, 制导律 (17) 不仅能够保证 滑模面 s将在固定时间 T1 内收敛,而且LOS角和LOS 角速率在固定时间 T1 + T2 内也是收敛的. 相较于有 限时间收敛制导律[10-15], T1 和 T2 只包含常值参数 l1、 l2、m1、m2、1、2、k1、k2, 并不依赖于制导系统的初 始状态,因此可以被预先设定. 注3 为了解决传统的固定时间收敛滑模面(13) 存在的非奇异问题, 本文提出的滑模面 (16) 在jx1j ⩽ " 时进行了滑模面转换, 这也导致了状态量 x = [x1; x2]T 最终并不能严格收敛到0, 只能收敛到区域 D 内, 但是通过选取足够小的 ", 系统的制导精度完全 能够得到满足. 2.3 扩张状态观测器(ESO)设计 实际情况中, 目标加速度 aT 通常是未知的, 并 且其上界值也很难得到, 为了保证制导律 (17) 有较 好的鲁棒性, 通常需要选取的 ∆ 足够大, 但是符号函 数 sign(s) 的存在会引发严重的颤振现象. 为了解决 这一问题, 本文引入扩张状态观测器 (extended state observer, ESO) 来对制导系统(4) 的外部扰动 d 进行实 时估计,并在导引指令中加以补偿. 与文献 [10] 设计类似, 本文构造如下 ESO (关于 ESO的收敛性证明,可参考文献[21]): e = z1 = _q; z2 r !1e 2 _rz1 _z1 = z2 = r!2fal(e; ; ): r cos(M q) r aM ; (24) 其中: z1 和 e 分别为 _q 的估计值和估计误差. z2 为 d 的 估计值. !1 和!2 为观测增益. fal的定义为 8<:jejsign(e); jej > ; 1 ; jej ⩽ ; e fal(e; ; ) = 0 < < 1; 0 < < 1: (25) 有了 d 的估计值 z2, 制导指令(17) 可以修改成如 下形式: ( r aM = cos(M q) l2 _g(x) + k1sign3s + k2sign4s 2 _rx2 r z2 r + ) + l11jx1j11x2+ : (26) 式 (26) 即为本文最终设计的带有攻击角度约束的 非 奇 异 终 端 滑 模 固 定 时 间 收 敛 制 导 律 (fixed-time convergence nonsingular terminal sliding mode guidance law, FTCNTSMG).
    第2期 3 仿真分析 李晓宝 等: 带攻击角度约束的非奇异终端滑模固定时间收敛制导律 479 假设导弹和目标的初始弹目距离 r0 = 10 km, 初 始LOS 角 q0 = 30°; 初始航迹角 M 0 = 60°; T 0° = 90°; 导弹和目标的速度 VM = 500 m/s; VT = 400 m/s; 目 标 的 加 速 度 aM = 7 g sin(/4). 参 照 文 献 [22], ESO 式(24) 中的参数取 1 = 0:5; = 0:01; !1 = 50; !2 = 100. FTCNTSMG 中 的 参 数 设 定 为 l1 = 0:2; l2 = 0:1; m1 = 1:8; m2 = 0:7; k1 = 1; k2 = 0:1; 1 = 1:5; 2 = 0:5; 1 = 1:25; 2 = 1:75; " = 0:001, 重力加速度g = 9:8 m/s2, 导弹的最大加速度 取20 g. 根据定理1计算得到T = 30:08 s. 注4 FTCNTSMG 中各种参数选择直接影响 T 的大小, 由于FTCNTSMG 给出的固定时间表示的是 任意初始条件下收敛时间的上界, T 一般设计的较 大, 通常导弹在拦截目标时状态量 X = [X1; X2]T, 实 际收敛时间要小于 T . 如果设计 T 太小, 在某些特殊 情况, 例如初始LOS 角误差 x1 较大时, 为了满足制导 律固定时间收敛的要求, 导弹需要有较强的机动能 力, 但是通常导弹的机动能力有限, 因此制导指令在 末制导初始阶段会出现饱和现象. 因此, 根据导弹末 制导机动能力的强弱, 需要通过调节FTCNTSMG 中 的参数来合理地设计T . 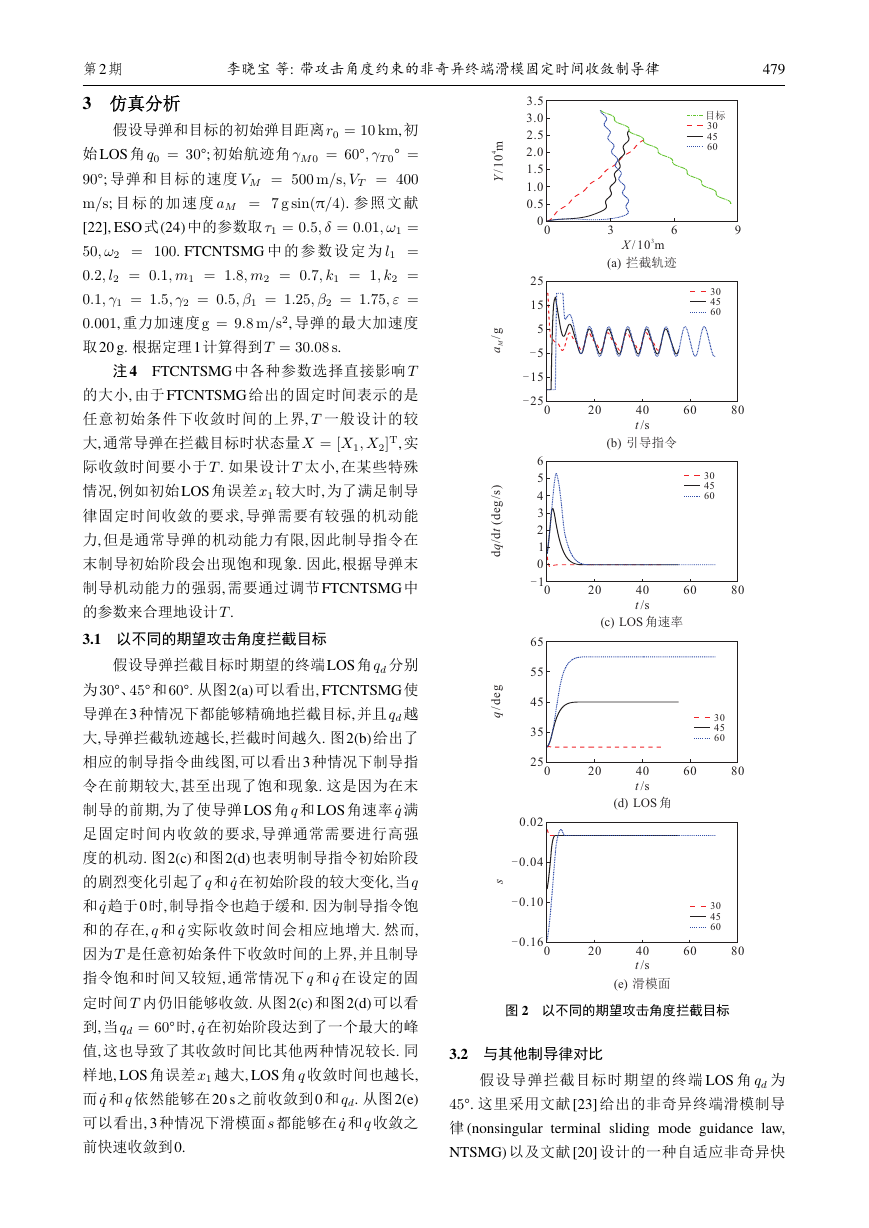3.1 以不同的期望攻击角度拦截目标 假设导弹拦截目标时期望的终端LOS 角 qd 分别 为 30°、45° 和 60°. 从图2(a) 可以看出, FTCNTSMG 使 导弹在3 种情况下都能够精确地拦截目标, 并且 qd 越 大, 导弹拦截轨迹越长, 拦截时间越久. 图2(b) 给出了 相应的制导指令曲线图, 可以看出3 种情况下制导指 令在前期较大, 甚至出现了饱和现象. 这是因为在末 制导的前期, 为了使导弹LOS 角 q 和LOS 角速率 _q 满 足固定时间内收敛的要求, 导弹通常需要进行高强 度的机动. 图2(c) 和图2(d) 也表明制导指令初始阶段 的剧烈变化引起了 q 和 _q 在初始阶段的较大变化,当q 和 _q 趋于0 时, 制导指令也趋于缓和. 因为制导指令饱 和的存在, q 和 _q 实际收敛时间会相应地增大. 然而, 因为 T 是任意初始条件下收敛时间的上界, 并且制导 指令饱和时间又较短, 通常情况下 q 和 _q 在设定的固 定时间 T 内仍旧能够收敛. 从图2(c) 和图2(d) 可以看 到, 当 qd = 60° 时, _q 在初始阶段达到了一个最大的峰 值, 这也导致了其收敛时间比其他两种情况较长. 同 样地, LOS 角误差 x1 越大, LOS 角 q 收敛时间也越长, 而 _q 和 q 依然能够在20 s 之前收敛到0 和 qd. 从图2(e) 可以看出, 3 种情况下滑模面 s 都能够在 _q 和 q 收敛之 前快速收敛到0. 图 2 以不同的期望攻击角度拦截目标 3.2 与其他制导律对比 假设导弹拦截目标时期望的终端 LOS 角 qd 为 45°. 这里采用文献 [23] 给出的非奇异终端滑模制导 律 (nonsingular terminal sliding mode guidance law, NTSMG) 以及文献 [20] 设计的一种自适应非奇异快 00X/10m3369(a)>ɮY/10m40.51.01.52.02.53.03.50204080(b)ᢣaM/g-2560t/s-15-5515250204080(c)LOSY΅᳛-160t/s0456123d/d(deg/s)qt0204080(d)LOSY60t/s25q/deg354555650204080(e)☢60t/ss-0.16-0.10-0.040.02L᪗30°45°60°30°45°60°30°45°60°30°45°60°30°45°60°
    480 控 制 与 决 策 第35卷 速终端滑模制导律(adaptive nonsingular fast terminal sliding mode guidance law, ANFTSMG) 进行仿真对比 分析. 文献[23]设计的滑模面和NTSMG分别为 s = x1 + x 2 ; 2 _r _q + _q2 cos(M q) r aM = (27) (28) + Msgmf(s) sign cos(M q) : 其中: 目标加速度 aT 假设是未知的, = M = 3 103 sgmf(s)的表达式为 5 3 ; = 1; 8<:sign(s); jsj > ; sgmf(s) = (1 + es)/(1 + es); jsj ⩽ ; = 0:002; = 1/: 文献[20]设计的滑模面和ANFTSMG分别为 (29) (30) (31) + l1x2 + l2 _g(x)+ r 2 _rx2 r s = x2 + l1x1 + l2g(x1); aM = cos(M q) ^∆sgmf(s) + k1sign1(s) + k2s [ 8<:sign(x1); jx1j > "; 1x1 + 2sign(x1)x2 _^∆ = jsj; ^∆(0) > 0; 其中 g(x1) = ] : 1; jx1j ⩽ "; l1 = 0:5; l2 = 0:5; = 2 3 ; = 1:1; k1 = 6; k2 = 2; 1 = 0:9; " = 0:001; = 0:002: 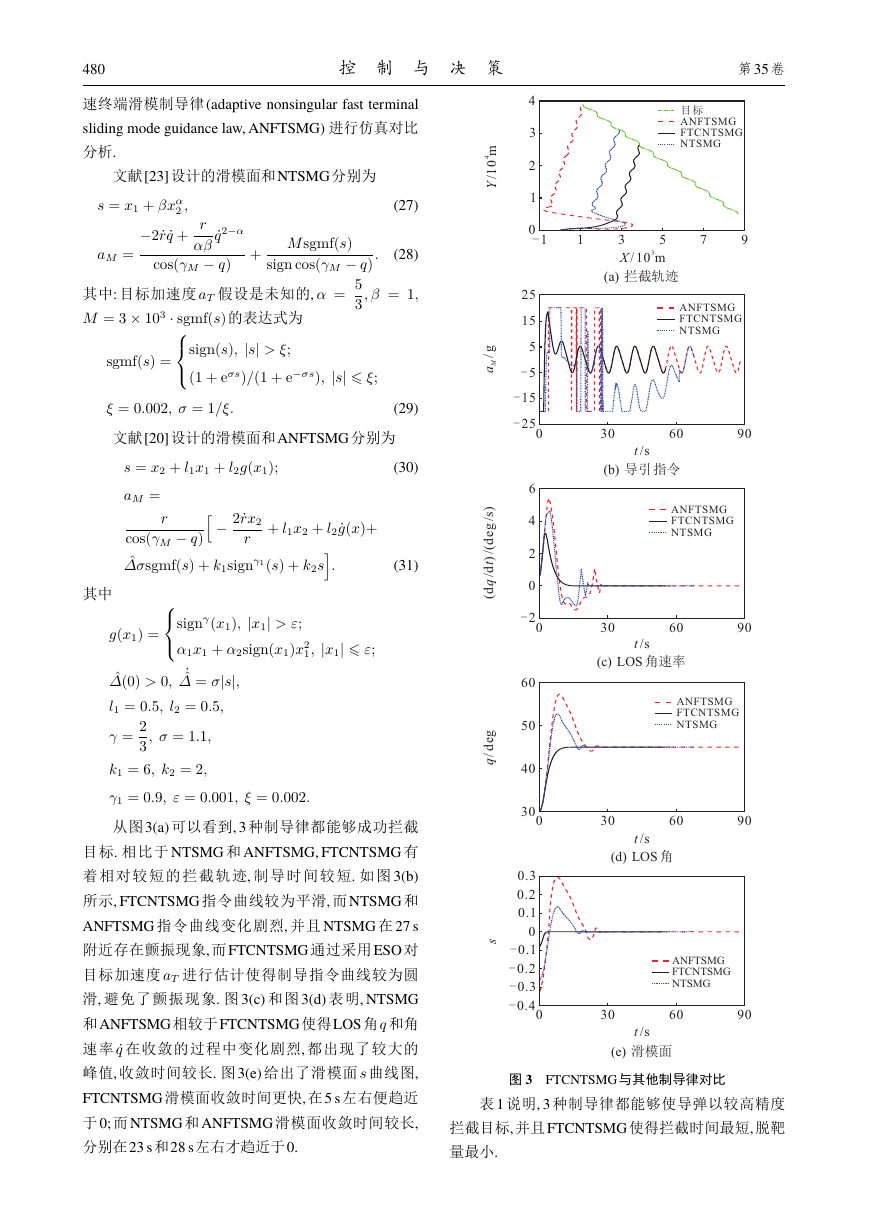从图3(a) 可以看到, 3 种制导律都能够成功拦截 目标. 相比于 NTSMG 和 ANFTSMG, FTCNTSMG 有 着 相 对 较 短 的 拦 截 轨 迹, 制 导 时 间 较 短. 如 图 3(b) 所示, FTCNTSMG 指令曲线较为平滑, 而NTSMG 和 ANFTSMG 指令曲线变化剧烈, 并且 NTSMG 在 27 s 附近存在颤振现象, 而FTCNTSMG 通过采用ESO 对 目标加速度 aT 进行估计使得制导指令曲线较为圆 滑, 避免了颤振现象. 图 3(c) 和图 3(d) 表明, NTSMG 和ANFTSMG 相较于FTCNTSMG 使得LOS 角 q 和角 速率 _q 在收敛的过程中变化剧烈, 都出现了较大的 峰值, 收敛时间较长. 图3(e) 给出了滑模面 s 曲线图, FTCNTSMG 滑模面收敛时间更快, 在5 s 左右便趋近 于0; 而NTSMG 和ANFTSMG 滑模面收敛时间较长, 分别在23 s和28 s左右才趋近于0. 图 3 FTCNTSMG 与其他制导律对比 表 1 说明, 3 种制导律都能够使导弹以较高精度 拦截目标, 并且FTCNTSMG 使得拦截时间最短, 脱靶 量最小. 057903090-2560-15-5515250-204620304050600-0.4-0.3L᪗ANFTSMGFTCNTSMGNTSMGANFTSMGFTCNTSMGNTSMGANFTSMGFTCNTSMGNTSMGANFTSMGFTCNTSMGNTSMGANFTSMGFTCNTSMGNTSMG123431-1309060309060309060-0.2-0.100.30.20.1X/10m3(a)>ɮY/10m4(b)ᢣaM/gt/s(c)LOSY΅᳛t/s(d/d(deg/s)qt)/(d)LOSYt/sq/deg(e)☢t/ss
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料