数据结构课程设计范文（多项式的加减乘除法）.doc

发布时间：2022-06-13 发布人：admin 分类：说明书资料大小：0.12M 资料格式：doc 举报版权申诉

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第1页.png

第1页 / 共12页

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第2页.png

第2页 / 共12页

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第3页.png

第3页 / 共12页

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第4页.png

第4页 / 共12页

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第5页.png

第5页 / 共12页

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第6页.png

第6页 / 共12页

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第7页.png

第7页 / 共12页

013e7944-a6ea-4e41-92da-09c370591042.doc.pdf-第8页.png

第8页 / 共12页

文本预览

《数据结构》课程设计报告书题系学目：多项式的加减乘法别：计算机科学与应用系号：学生姓名：指导教师：完成日期： 12 月 9 日

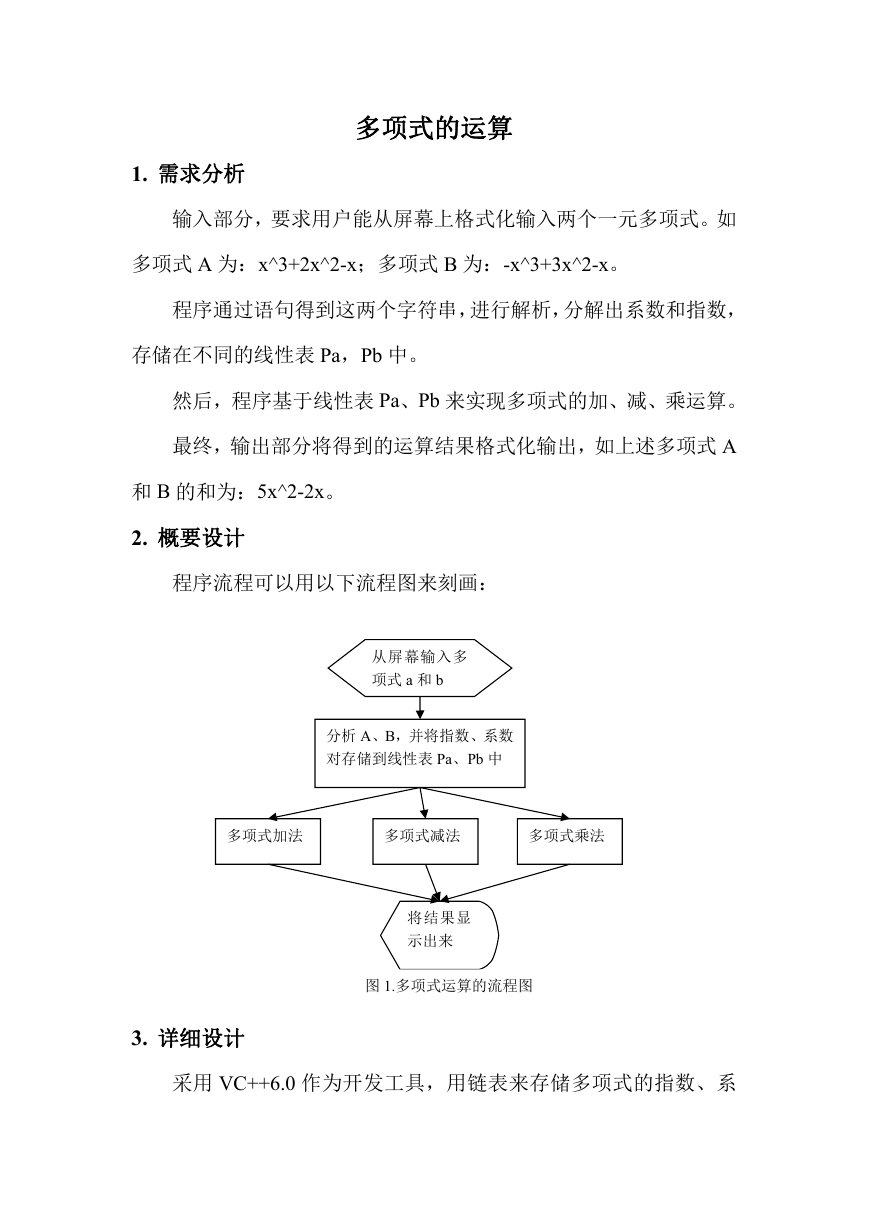
多项式的运算 1. 需求分析输入部分，要求用户能从屏幕上格式化输入两个一元多项式。如多项式 A 为：x^3+2x^2-x；多项式 B 为：-x^3+3x^2-x。程序通过语句得到这两个字符串，进行解析，分解出系数和指数，存储在不同的线性表 Pa，Pb 中。然后，程序基于线性表 Pa、Pb 来实现多项式的加、减、乘运算。最终，输出部分将得到的运算结果格式化输出，如上述多项式 A 和 B 的和为：5x^2-2x。 2. 概要设计程序流程可以用以下流程图来刻画：从屏幕输入多项式 a 和 b 分析 A、B，并将指数、系数对存储到线性表 Pa、Pb 中多项式加法多项式减法多项式乘法将结果显示出来图 1.多项式运算的流程图 3. 详细设计采用 VC++6.0 作为开发工具，用链表来存储多项式的指数、系

数对，为多项式开发一个多项式类，其中有成员函数加、减、乘、除。 3.1 函数和结构体的声明用 C 中的结构体来描述一个多项式的系数和指数，定义如下： struct term { //项的表示，多项式的项作为 LinkList 的数据元素 float coef; //系数 int expn; //指数 struct term *next; } 3.2 主要函数简介 A. term* CreatPolyn(term *P,int m) 函数的功能：输入 m 项的系数和指数，建立表示一元多项式的有序链表 P 函数的参数：整型变量 m，表示多项式的项数实型变量 coef; 表示多项式的系数整型变量 expn, 表示多项式的指数函数返回值：一个多项式 B. void PrintfPoly(term *P) 函数的功能：输出一元多项式函数的参数：实型变量 coef; 表示多项式的系数整型变量 expn, 表示多项式的指数

函数返回值：无 term* APolyn(term *Pa, term *Pb) 函数的功能：输出一元多项式函数的参数：实型变量 coef; 表示多项式的系数整型变量 expn, 表示多项式的指数函数返回值：无 4. 调试分析在设计过程中主要遇到下列问题：（1）多项式的显示方法：比如是降幂还是升幂排列，哪种排列方式更符合人们经常的习惯，是人一目了然，可读性强。通过与同学讨论得出结果，应用降幂排列。（2）结构体的一些具体用法：结构体的应用不是很熟练，在调试中经常出错，此问题经过查资料与问老师后得到解决。 5．源代码 #include #include #include typedef struct term { //项的表示，多项式的项作为 LinkList 的数据元素 float coef; //系数 int expn; //指数 struct term *next; }term; term* CreatPolyn(term *P,int m) { // // 输入 m 项的系数和指数，建立表示一元多项式的有序链表 P if(m <= 0) return NULL;

term *h = P = (term*)malloc(sizeof(term)), *q; P->coef = 0.0; int i; printf("依次输入%d 个非零项\n",m); for (i = 1; i <= m; ++i) { // 依次输入 m 个非零项 scanf("%f%d",&P->coef,&P->expn); if(P->coef) q = P; P = P->next = (term*)malloc(sizeof(term)); } q->next = NULL; free(P); return h; } // CreatPolyn term* selsort(term *h) { term *g, *p, *q; if(!h) return NULL; float f; int i, fini = 1; for(g = h;g->next&&fini;g = g->next) { fini = 0; for(p = h,q = h->next;q;p = p->next,q = q->next) if (p->expn < q->expn) { f = p->coef;i = p->expn; p->coef = q->coef;p->expn = q->expn; q->coef = f;q->expn = i; fini = 1; } } for(g = h,p = g->next;p;) if(g->expn==p->expn) { g->coef += p->coef; g->next = p->next; q = p; p = p->next; free(q); }

else if(g->next) { g = g->next; p = p->next; } return h; } void PrintfPoly(term *P) { term *q = P; if(!q) { putchar('0'); return; } if(q->coef!=1) { printf("%g",q->coef); if(q->expn==1) putchar('X'); else if(q->expn) printf("X^%d",q->expn); } else if(!q->expn) putchar('1'); else if(q->expn==1) putchar('X'); else printf("X^%d",q->expn); q = q->next; while (q) { if(q->coef > 0) putchar('+'); if(q->coef!=1) { printf("%g",q->coef); if(q->expn==1) putchar('X'); else if(q->expn) printf("X^%d",q->expn); } else if(!q->expn) putchar('1'); else if(q->expn==1) putchar('X'); else printf("X^%d",q->expn); q = q->next; } } Compare(term *a, term *b) {

if (a->expn < b->expn) return -1; if (a->expn > b->expn) return 1; return 0; } term* APolyn(term *Pa, term *Pb) { // 多项式加法：Pa = Pa＋Pb，利用两个多项式的结点构成"和多项式"。 term *h, *qa = Pa, *qb = Pb, *p, *q; float sum; h = p = (term*)malloc(sizeof(term)); p->next = NULL; while (qa && qb) { // Pa 和 Pb 均非空 switch (Compare(qa,qb)) { case -1: // 多项式 PA 中当前结点的指数值小 p->next = qb; p = qb; qb = qb->next; break; case 0: // 两者的指数值相等 sum = qa->coef + qb->coef; if (sum != 0.0) { // 修改多项式 PA 中当前结点的系数值 p->next = qa; qa->coef = sum; p = qa; qa = qa->next; } else { // 删除多项式 PA 中当前结点 q = qa; qa = qa->next; free(q); } q = qb; qb = qb->next; free(q); break; case 1: // 多项式 PB 中当前结点的指数值小 p->next = qa; p = qa; qa = qa->next;

break; } // switch } // while if (Pa) p->next = qa; // 链接 Pa 中剩余结点 if (Pb) p->next = qb; // 链接 Pb 中剩余结点 q = h; h = h->next; free(q); return h; } // APolyn term* A(term *Pa, term *Pb) { int n; puts("再输入一一元多项式的项数"); scanf("%d",&n); Pb = CreatPolyn(Pb,n); Pb = selsort(Pb); PrintfPoly(Pa); if(Pb && Pb->coef>0) printf(" + "); PrintfPoly(Pb); Pa = APolyn(Pa,Pb); printf(" = "); Pa = selsort(Pa); PrintfPoly(Pa); return Pa; } term* BPolyn(term *Pa, term *Pb) { // 多项式减法：Pa = Pa-Pb，利用两个多项式的结点构成"差多项式"。 term *p = Pb; while(p) { p->coef *= -1; p = p->next; } return APolyn(Pa,Pb); } // BPolyn term* B(term *Pa, term *Pb) { int n; puts("再输入一一元多项式的项数");

分享到：

赞收藏

资料库

数据结构课程设计范文（多项式的加减乘除法）.doc

相关推荐

课程资源

热门标签

最新资料