利用 Hopfield 网络的解决 TSP 旅行商问题 专业：信号与信息处理 学号：20104228033 姓名：曹发海 一、实验背景 TSP 问题即所谓的旅行商问题 ( Traveling Salesman Problem)，问题的提法是：在 N 个城市中各经历一次后回到出发点，使所经过的路程最短。其不同选择方案有 N ! / 2 N 种，在城市数较少的情况下可以用枚举等方法，但如果城市数量较大时，使用 枚举法求解就要考虑的情况是数量级，计算量之大是不可想象的。将 Hopfield 网络 应用于求解 TSP 问题，效果是显著的。在 1985 年 Hopfield 和 D. W. Tank 用循环网求 解 TSP。试验表明当城市的个数较少时，可以给出最优解。当城市个数较多而不超过 30 时，多可以给出最优解的近似解，而当城市的个数超过 30 时，最终的结果就不太 理想了。 二、实验目的 1、掌握 Hopfield 网络算法的原理 2、掌握 TSP 旅行商问题的本质 3、利用 Hopfield 网络的解决 TSP 旅行商问题，用 Matlab 程序实现 三、实验原理 Hopfield 神经网络是高维非线性系统，可能有许多稳定优态。从任何初始状态开 始运动，总可以到某个稳定状态。这些稳定状态可以通过改变网络参数得到。基本思 想：建立一个拥有 N*N 的神经元，带反馈的网络，首先给网络设置一组初始权值， 然后经过多次迭代计算，改变网络能量和神经元状态。当网络能量不再降低时.神经元 的输出矩阵即为问题的解。具体步骤: 1、把 TSP 问题映射为换位矩阵，表示每一条可能路径，并写出相应的距离表达 式。 2、把 TSP 问题的换位矩阵与 N*N 神经元的网络相对应，每个路径对应的换位矩 阵的各元素与相应的神经元稳态输出相对应。 3、构造反映 TSP 问题约束条件的能量函数 E，使 E 的极小值点对应于 TSP 问题 的解。 4、由能量函数对应出神经网络的权值矩阵[ 5、给定网络的初始状态，运行网络直至收敛稳定，则网络的稳态输出即对应 TSP ijw ]。 问题的局部优化解 解决问题需要说明的是以下几个量：N 个城市间存在 N ! / 2 N 条可能路径设问 题中含有 N 个城市，用 N 3N 个神经元构成网络，dxy 为城市 X 与城市 Y 之间的距 离，y xi 为城市 X 的第 i 个神经元的状态: ,xi yjw 为城市 X 的第 i 个神经元到城市 Y 的第 j 个神经元的连接权。网络的能 量函数 E 

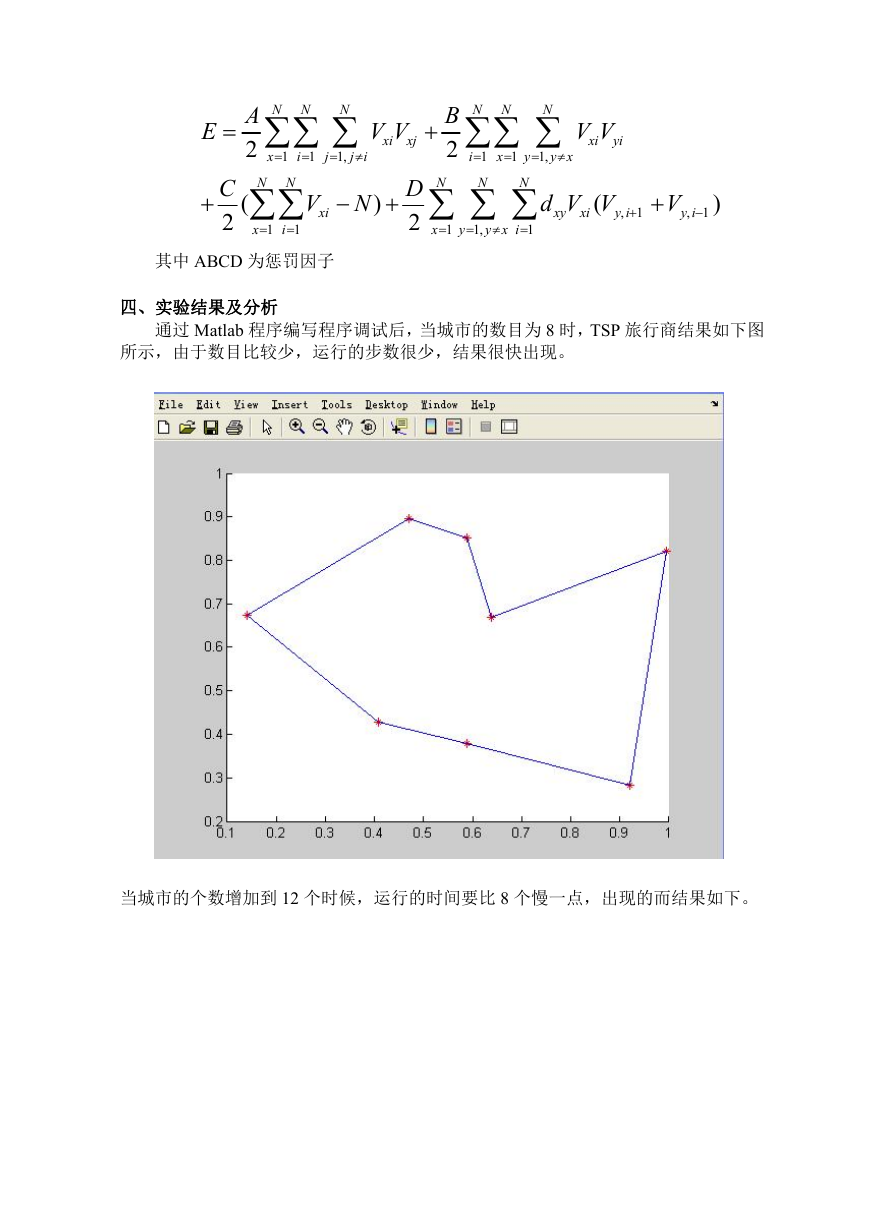
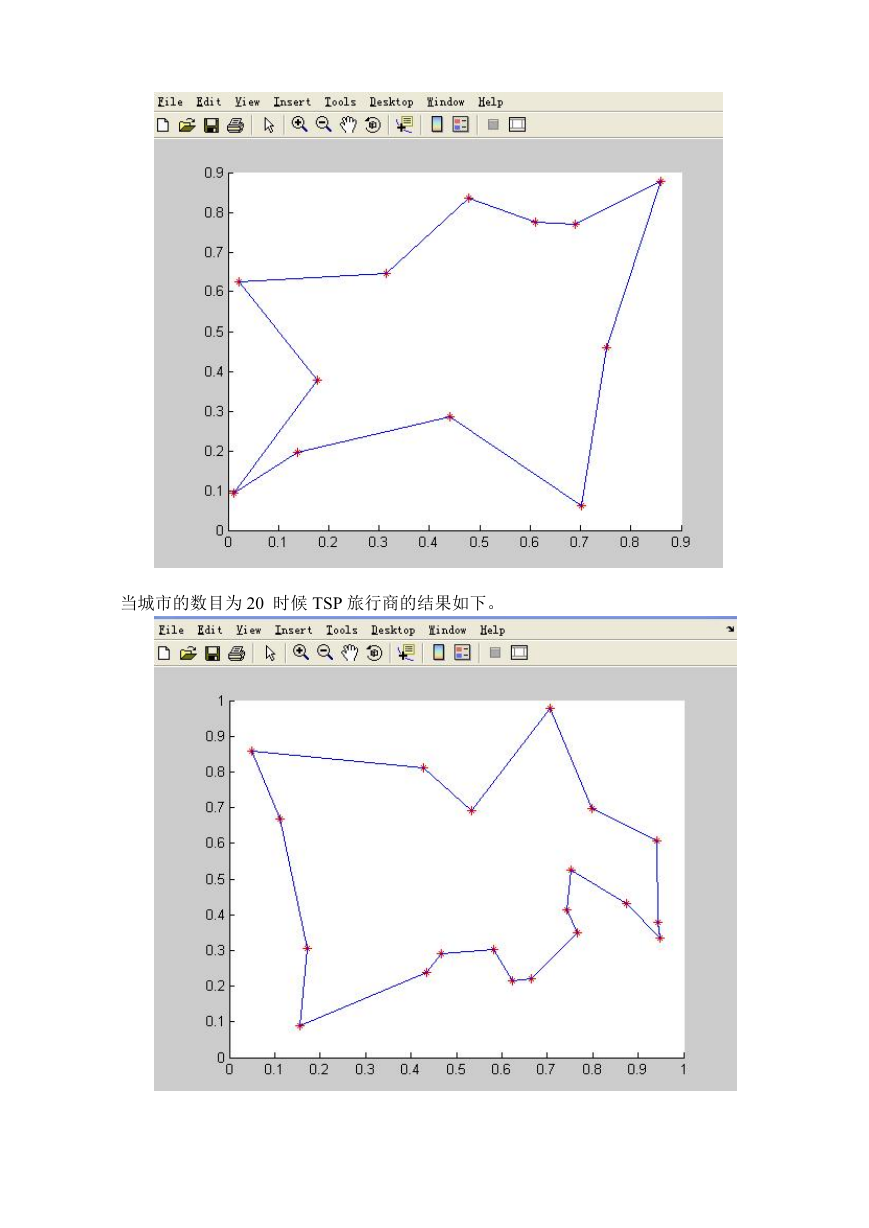
x N A 2 N  1  N i x 1  i 1  ( E   C 2 N N   1  j 1,  j  V V xi xj i V xi  N )  D 2 V V xi yi  N N N   B 2    1  N y N 1,  1  N x i x 1  y 1,  y x i  1  y x  ( d V V xy xi , 1 y i   V , 1 y i  ) 其中 ABCD 为惩罚因子 四、实验结果及分析 通过 Matlab 程序编写程序调试后，当城市的数目为 8 时，TSP 旅行商结果如下图 所示，由于数目比较少，运行的步数很少，结果很快出现。 当城市的个数增加到 12 个时候，运行的时间要比 8 个慢一点，出现的而结果如下。 

当城市的数目为 20 时候 TSP 旅行商的结果如下。 

当结果超过 25 以上时，基本上不出现结果，甚至死机，可见 hopfield 网络的 TSP 旅行商问题还是有数目限制的，当达到一定数目时，可能就需要寻找别的方法去解决。 五、实验小结 1、通过实验掌握了 Hopfield 网络算法的原理 2、在求解的途中掌握了 TSP 旅行商问题的本质 3、学会了利用 Hopfield 网络的解决 TSP 旅行商问题并用 Matlab 程序实现该功能 4、城市数目的限制过多时，Hopfield 网络的解决 TSP 旅行商问题仍然存在不足 附实验主程序 clc;clear all; Maxsize=100;MaxDis=100000;Em=0;Ep=0; n=8; test=100+n^2; cycle=100+10*(n-5); summin=0;dis=zeros(1,test); A=500;B=500;D=500;C=200;u0=0.02;lan=1.0000e-005;delta=0.1; city=rand(2,n); place=city; betterpath=ones(1,n+1); for k=1:n d(k,k)=0; for k1=k+1:n d(k,k1)=sqrt((place(1,k)-place(1,k1))^2+(place(2,k)-place(2,k1))^2); d(k1,k)=d(k,k1); end end for tk=1:test del_pre=0; u=1/n+(2*rand(n)-1)*delta/n; v=zeros(n); for ck=1:cycle [del,v]=Newv(u,v,u0,n); if(abs(del-del_pre)<(1e-15)) break; end del_pre=del; [u]=Newu_ad(u,v,d,n); end 

[Em,Ep]=Energy(d,v,n); end [n_zuiyou,n_ciyou]=Count(test,path,dis,summin,n_fre,n_ill); Em=Em/test; Ep=Ep/test; figure(1);hold on for k=1:n plot(city(1,k),city(2,k),'r*') end for k=1:n [path,n_fre,n_ill,betterpath,dis(tk),summin]= Check(tk,ck,v,d,cycle,n,betterpath,summin); place(:,k)=city(:,betterpath(k)); end place(:,n+1)=city(:,betterpath(1)); plot(place(1,:),place(2,:));