第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
comsol 石墨烯模拟.pdf
applications. The
Models for Simulation Based Selection of 3D Multilayered
Graphene Biosensors
E. Lacatus *1, G.C. Alecu1, and A. Tudor1
1Polytechnic University of Bucharest
* E. Lacatus: elena.lacatus@upb.ro
Abstract: At the forefront of a new generation
of sensors grapheme and grapheme composite
materials are intensively studied for medical and
biosensing
outstanding
electrical, mechanical and quantum properties of
grapheme make them a promising material
solution to overlap the existing gap between
biological and non-biological systems into a
continuum like-viscoelastic integrated model.
Through COMSOL Multiphysics ® modeling and
simulation were
fitted
solutions for a multilayered biosensing device
structure from the presently known graphene
(G), graphene- oxide (GO) and composite
materials including different forms of graphene (
graphene nanoribbons –GNRs, reactive graphene
oxide –RGO, and TWEEN paper –TwGP).
Keywords: graphene, biosensor, Fröhlich
quantum
non-linear
thermodynamics
1. Introduction
Figure 2. Basic and functionalized graphene
structures (ChemBio 3D Ultra©)
coherence,
identified
the best
phonon,
a
b
Figure 1. (a) Graphene model; (b) Functionalized
bilayer-graphene structure (ChemBio 3D Ultra©)
Intensely studied in the last decade, graphene
(G), graphene oxides (GO), reactive graphene
oxides (RGO), graphene nanoribbons (GNRs)
and many other graphene based composite
materials are continuously approach
the
medical and biosensing area with the aim of
defining new material solutions for properly
personalized medical
and
therapeutic solutions.
applications
to
With large similarities to the surface of
graphite (Figure 1), graphene (G) can adsorb and
desorb different type of atoms and molecules,
remaining highly conductive [1]. This property
can be used for sensor applications. It is largely
known that single- layer graphene (1G) is much
more reactive than 2G, 3G (<10 layers) graphene
multilayer structures [2,3]. However, the edge of
the graphene is more reactive than the surface,
graphene being a fairly inert material, and thus
an ideal candidate for bio-sensors.
;
a
b
Figure 3. MATLAB© models of electronic properties
of graphene :(a) 20 atoms – armchair structure;
(b) 20 atoms – zig-zag structure
Excerpt from the Proceedings of the 2015 COMSOL Conference in Grenoble
The aim of the modeling and simulation of the
multilayered graphene structures
is mainly
focused on the device response at different types
of energy stimulus reaching the active surfaces
of the 3D bio-sensing structures under the main
restrictions of biocompatibility and non-toxicity
(Figure 2, Figure 3).
2. Models Definition
The most accessible and nonintrusive
interface of a sensor with humans is on the skin
surface. Not only because skin is the organ that
has the widest area of the human body, but
because it has differentiated responses to internal
and external stimuli, thus being an accessible
environment for physical and chemical data
gathering.Based on FET (Field Effect Transistor)
properties [15,17] that can relate human skin to
the
of
G/GO/TwGP [1,4,5,13,16,18] two biosensing
devices were designed (Figure 4 c, d).
characteristics
presently
known
Figure 4 Multilayer graphene sensing concepts:
(a),(b) General GNRs multilayer concept [4,18] (c) single
layer G/GO sensor; (d) multilayer G/GO/TwGP sensor
–
structure
graphene
For these studies were considered the main
interfaces between: human skin – hydrogel
(PVA Hydrogel); PVA
polymer
Hydrogel
based module
(G/GO/TwGP); graphene module – electrodes
(Ag); graphene/electrodes – substrate (Silica
glass SiO2) (Figure 4 c, d).For each of these
to
interfaces were
describe
process
microvariables as well as the environmental
stimuli influences (macrovariables) as follows:
identified models able
evolution
the
the
of
• Two electrodes biosensing module (Figure
4c) including skin, PVA Hydrogel, graphene
(G) and graphene-oxide (GO) functionalized
with different proteins (Alpha Helix, Loricin
and Lysozyme)
• Four electrodes module (Figure 4 d) that
considers the same main interfaces with both
graphene composite structure and without it,
for the same environmental stimuli, in order to
objectively
graphene
responses (Figure 5,…15)
differentiate
the
All
these models are having
the same
continuum-like background of
a biosensor
device structure based on weak van der Waals
interaction forces that describe the nonlinear
into a surrounding
behavior of graphene
viscoelastic
environment
classical
Kirchhoff plate theory [14]
through
In the Equation 1, used for modeling single
layer graphene vibration response based on
Kirchhoff plate theory [14] α1 and α3 represents
the linear and nonlinear interaction forces:
(1)
where: Nx, Ny are biaxial in-plane loads; a,
b- length, width of the single layer graphene; h-
thickness of the single layer graphene; p –
distributed transverse load per unit area (due to
surrounding medium effect) ; D is the bending
stiffness of the plate:
E is the Young’s modulus; ν – Poisson’s
(2)
ratio; ρ – mass density;
- Laplace operator:
(3)
is properly described
The density of charge, characterizing all
through
interfaces,
nonlinear
thermodynamics with electron –
phonon (ē – ph) , phonon – phonon (ph – ph) and
ion –phonon interactions. Thus for all models
were studied the charge density distributions of
electric,
thermal and acoustic field stimuli
responsible for (ē – ph), (ph – ph) and (ion –ph)
interactions (Figures 5,…, 15).
Excerpt from the Proceedings of the 2015 COMSOL Conference in Grenoble
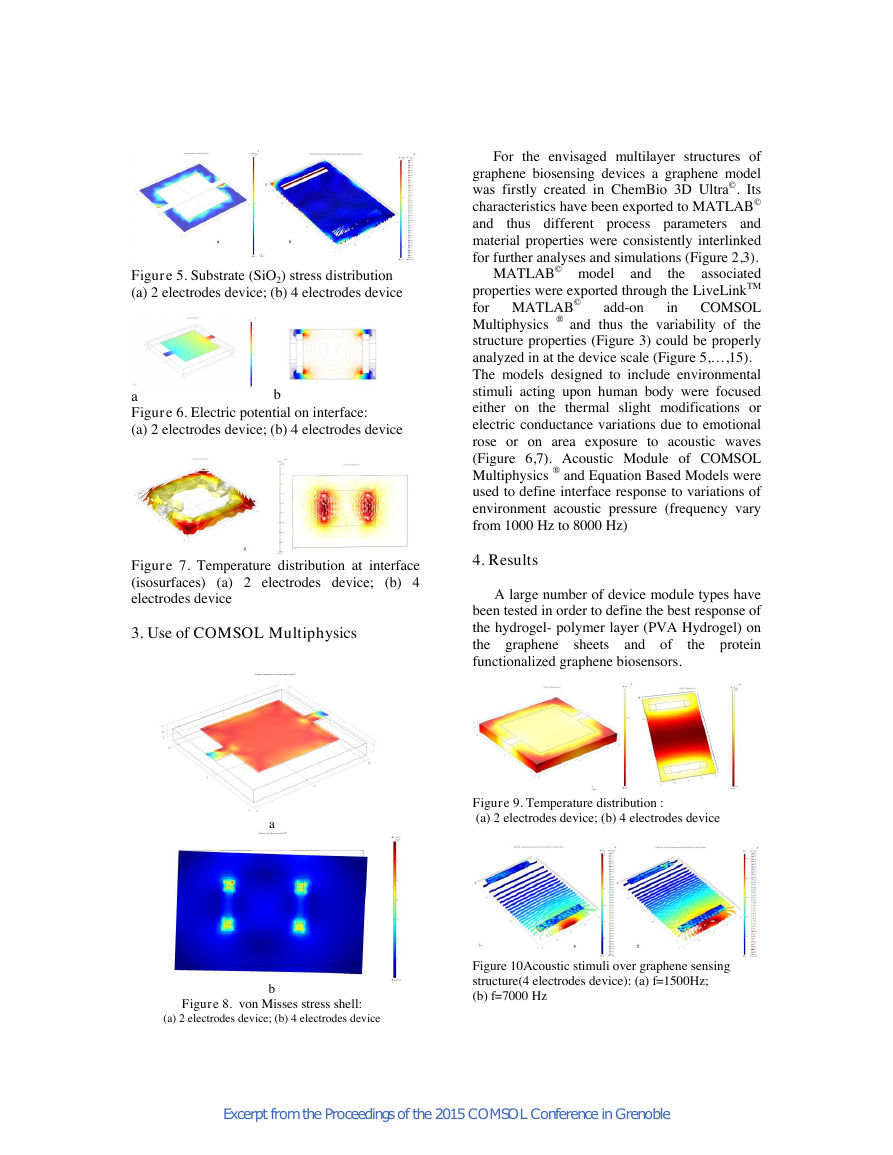
Figure 5. Substrate (SiO2) stress distribution
(a) 2 electrodes device; (b) 4 electrodes device
b
a
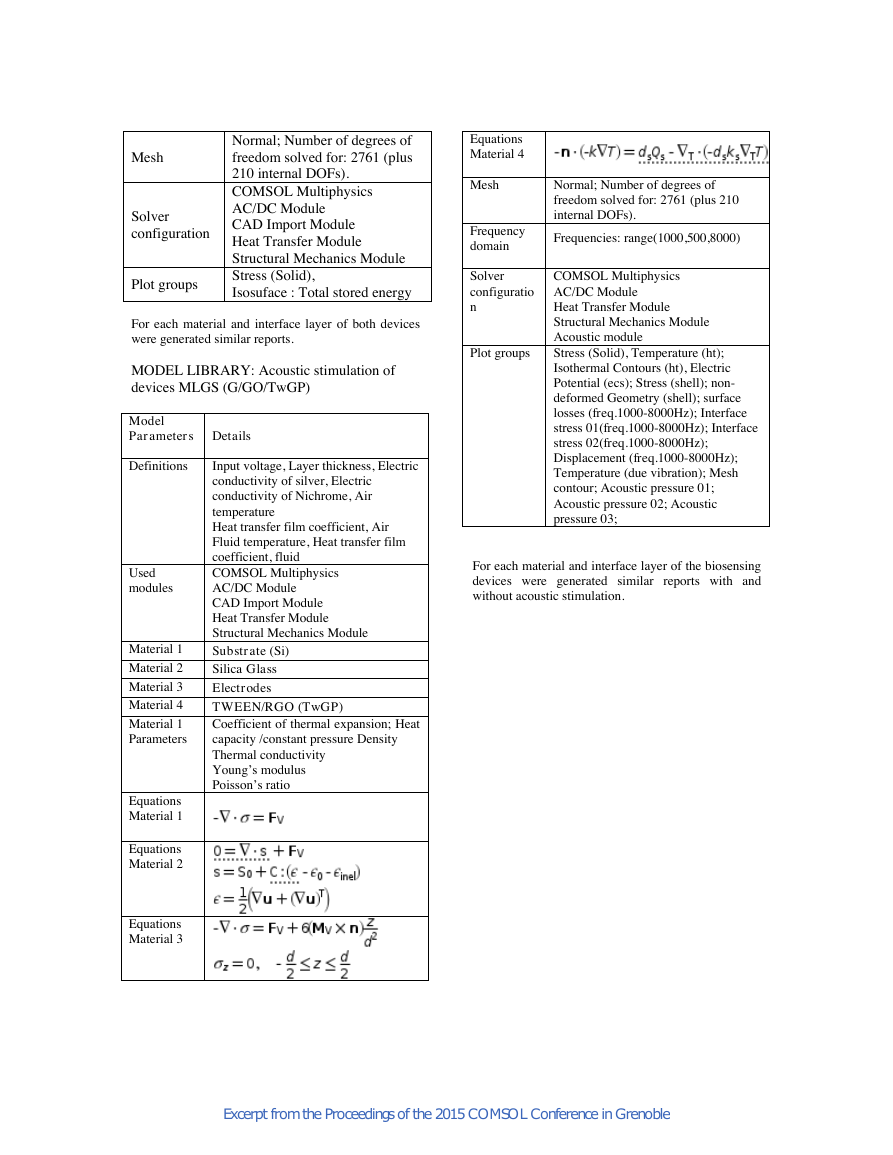
Figure 6. Electric potential on interface:
(a) 2 electrodes device; (b) 4 electrodes device
Figure 7. Temperature distribution at interface
(isosurfaces) (a) 2 electrodes device; (b) 4
electrodes device
3. Use of COMSOL Multiphysics
add-on
MATLAB© model and
For the envisaged multilayer structures of
graphene biosensing devices a graphene model
was firstly created in ChemBio 3D Ultra©. Its
characteristics have been exported to MATLAB©
and
thus different process parameters and
material properties were consistently interlinked
for further analyses and simulations (Figure 2,3).
the associated
properties were exported through the LiveLinkTM
for MATLAB©
in COMSOL
Multiphysics ® and thus the variability of the
structure properties (Figure 3) could be properly
analyzed in at the device scale (Figure 5,…,15).
The models designed to include environmental
stimuli acting upon human body were focused
either on the thermal slight modifications or
electric conductance variations due to emotional
rose or on area exposure to acoustic waves
(Figure 6,7). Acoustic Module of COMSOL
Multiphysics ® and Equation Based Models were
used to define interface response to variations of
environment acoustic pressure (frequency vary
from 1000 Hz to 8000 Hz)
4. Results
A large number of device module types have
been tested in order to define the best response of
the hydrogel- polymer layer (PVA Hydrogel) on
the graphene sheets and of
the protein
functionalized graphene biosensors.
a
b
Figure 8. von Misses stress shell:
(a) 2 electrodes device; (b) 4 electrodes device
Figure 9. Temperature distribution :
(a) 2 electrodes device; (b) 4 electrodes device
Figure 10Acoustic stimuli over graphene sensing
structure(4 electrodes device): (a) f=1500Hz;
(b) f=7000 Hz
Excerpt from the Proceedings of the 2015 COMSOL Conference in Grenoble
For each of these modules the biologic
responses and the field excitations have to reach
simultaneity under the COMSOL Multiphysics ®
model (Figure 4).
a
Figure 11 Pressure distribution (skin-polymer)/sensor
interface: (a) 2 electrodes device; (b) 4 electrodes
device
Figure 12 Spatial distribution of flux energy on
graphene bisensor (4 electrodes device)
.
Figure 13 Interfaces charge distributions (4 electrodes
device)
Figure 14 Membrane stress under environmental
stimuli: 2 electrodes device
Figure 15 Interface stress under environmental stimuli:
(a) 2 electrodes device; (b) 4 electrodes device
5. Discussion
The analyzed biosensing device models,
regardless their design solution (two or four
electrodes; single- or multilayer graphene;
graphene composite material) revealed through
simulations output data the “sensing” ability of
the graphene –based concept model.
For each module type the graphene/ graphene
composite materials generate clearly differentiate
the environmental stimuli, or
responses
process microvariables
thus
confirming the biosensing ability of this class of
materials.
evolution,
to
Operating with a continuum model for all
interfaces (ē – ph, ph – ph and ion –ph) and
harvesting biological charge density variations to
relate them to environment stimuli, the 3D
multilayered graphene biosensors models and
simulations offered valuable design solutions
6. Conclusions
Making the best use of the flexible modules of
COMSOL Multiphysics ® the most relevant
device properties of the multilayered graphene
biocompatible structures could be determined
and, mostly important, could be related to the
complex interface phenomena at human skin
level.
Excerpt from the Proceedings of the 2015 COMSOL Conference in Grenoble
7. References
1. J.-C Charlier, et al., Electron and Phonon
Properties of Graphene: Their Relationshop
with Carbon Nanotubes , Carbon Nanotubes,
Springer-Verlag, Berlin,
http://dx.doi.org/10.1007/978-3-540-72865-
8_21, (2008)
2. H.
Fröhlich
, F. Kremer, Coherent
Excitations in Biological Systems , Springer-
Verlag, ISBN 978-3-642-69186-7,(1983)
3. H.Fröhlich, Biological Coherence
and
Response to External Stimuli , Springer,
ISBN 978-3-642-73309-3, (1988)
4. A.K. Geim, K.S. Novoselov , The rise of
graphene. Nat. Mater. 6, 183, (2007)
5. O. Heinonen, P.L. Taylor, A Quantum
Approach to Condensed Matter Physics;
Cambridge University Press: Cambridge,
UK, 2002.
6. B. Hille,
Ion Channels of Excitable
Membranes, Sinauer, (2001)
7. E.
Lacatus, Engineering Self-Assembly
through Modeling Nanostructures, EngOpt
2010, The 2nd International Conference on
Engineering Optimization, 6-9 September
2010, Lisbon, Portugal, ISBN 978-989-
96264-3-0, (2010)
ASME
8. E. Lacatus, F.A. Savulescu, Nano-Bio-Cogno
Model of Acoustic Patterning for Molecular
Neurostimulation,
Proceedings
DOI:10.1115/FMD2013-16178, (2013)
9. E. Lacatus, Ion Channel Path of Cellular
Transduction, Biochimica et Biophysica Acta
(BBA), Bioenergetics Volume 1837, p.110-
111, DOI: 10.1016/j.bbabio.2014.05.266,
(2014)
10. E. Lacatus, et al., Analysis of 3D
Biocompatible Additive Structure Using
COMSOL
Software,
COMSOL Conference , Cambridge , (2014)
Multiphysics®
11. E. Lacatus, et al., From Music to Non-
COMSOL
COMSOL
Invasive
Multiphysics®
Conference, Cambridge, (2014)
Therapies
Models,
via
12. E. Lacatus, Modeling a Multilayered
Graphene
6th
International conference on Advanced Nano
Materials, Aveiro, (2015)
Biosensing
Structure,
13. D.L. Mafra, P.T. Araujo,
Intra- and
Interlayer Electron-Phonon Interactions in
BiLayer Graphene, Appl. Sci. 2014, 4, 207-
239; doi:10.3390/app4020207, (2014)
14. M.H. Mahdavi et al., Nonlinear vibration and
postbuckling analysis of a single
layer
graphene sheet embedded in a polymer
matrix, Physica E 44 1708–1715, (2012)
15. M.V. Mesquita et al., Systems Biology: An
Information-Theoretic-Based
Thermo-
Statistical Approach, Brazilian Journal of
Physics, vol. 34, no. 2A, June, (2004)
16. A.H.C. Neto et al., The electronic properties
of graphene. Rev. Mod. Phys. 81, 109–162,
(2009)
17. P.V. Tsaklis, Presentation of acoustic waves’
propagation and their effects through human
body tissues, Human Movement, 58, vol. 11
(1), 58–65, DOI: 10.2478/v10038- 009-
0025-z, (2010)
18. D. Verma et al., Vibration mode localization
single- and multi-layered graphene
Computational Materials
in
Nanoribbons,
Science 95,41–52, (2014)
8. Appendix
MODEL LIBRARY: Device SLGS (G/GO)
E.g.: Material 1 -Silica Glass
Model
Parameters
Details
Input voltage, Layer thickness,
Electric conductivity of silver,
Electric conductivity of
Nichrome, Air temperature
Heat transfer film coefficient,
Air Fluid temperature, Heat
transfer film coefficient, fluid
Silica Glass
Coefficient
expansion
Heat capacity /constant pressure
Density, Thermal conductivity
Young's modulus
,Poisson's
ratio
thermal
of
Definitions
Material 1
Material 1
Parameters
Equations
Material 1
Excerpt from the Proceedings of the 2015 COMSOL Conference in Grenoble
Equations
Material 4
Mesh
Frequency
domain
Solver
configuratio
n
Plot groups
Normal; Number of degrees of
freedom solved for: 2761 (plus 210
internal DOFs).
Frequencies: range(1000,500,8000)
COMSOL Multiphysics
AC/DC Module
Heat Transfer Module
Structural Mechanics Module
Acoustic module
Stress (Solid), Temperature (ht);
Isothermal Contours (ht), Electric
Potential (ecs); Stress (shell); non-
deformed Geometry (shell); surface
losses (freq.1000-8000Hz); Interface
stress 01(freq.1000-8000Hz); Interface
stress 02(freq.1000-8000Hz);
Displacement (freq.1000-8000Hz);
Temperature (due vibration); Mesh
contour; Acoustic pressure 01;
Acoustic pressure 02; Acoustic
pressure 03;
For each material and interface layer of the biosensing
devices were generated similar reports with and
without acoustic stimulation.
Mesh
Solver
configuration
Plot groups
Normal; Number of degrees of
freedom solved for: 2761 (plus
210 internal DOFs).
COMSOL Multiphysics
AC/DC Module
CAD Import Module
Heat Transfer Module
Structural Mechanics Module
Stress (Solid),
Isosuface : Total stored energy
For each material and interface layer of both devices
were generated similar reports.
MODEL LIBRARY: Acoustic stimulation of
devices MLGS (G/GO/TwGP)
Model
Parameters Details
Definitions
Used
modules
Material 1
Material 2
Material 3
Material 4
Material 1
Parameters
Equations
Material 1
Equations
Material 2
Equations
Material 3
Input voltage, Layer thickness, Electric
conductivity of silver, Electric
conductivity of Nichrome, Air
temperature
Heat transfer film coefficient, Air
Fluid temperature, Heat transfer film
coefficient, fluid
COMSOL Multiphysics
AC/DC Module
CAD Import Module
Heat Transfer Module
Structural Mechanics Module
Substrate (Si)
Silica Glass
Electrodes
TWEEN/RGO (TwGP)
Coefficient of thermal expansion; Heat
capacity /constant pressure Density
Thermal conductivity
Young’s modulus
Poisson’s ratio
Excerpt from the Proceedings of the 2015 COMSOL Conference in Grenoble
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
