第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
用希尔伯特黄变换（HHT）求时频谱和边际谱.doc
用希尔伯特黄变换（HHT）求时频谱和边际谱
1.什么是 HHT？
HHT 就是先将信号进行经验模态分解（EMD 分解），然后将分解后的每个 IMF 分量进
行 Hilbert 变换，得到信号的时频属性的一种时频分析方法。
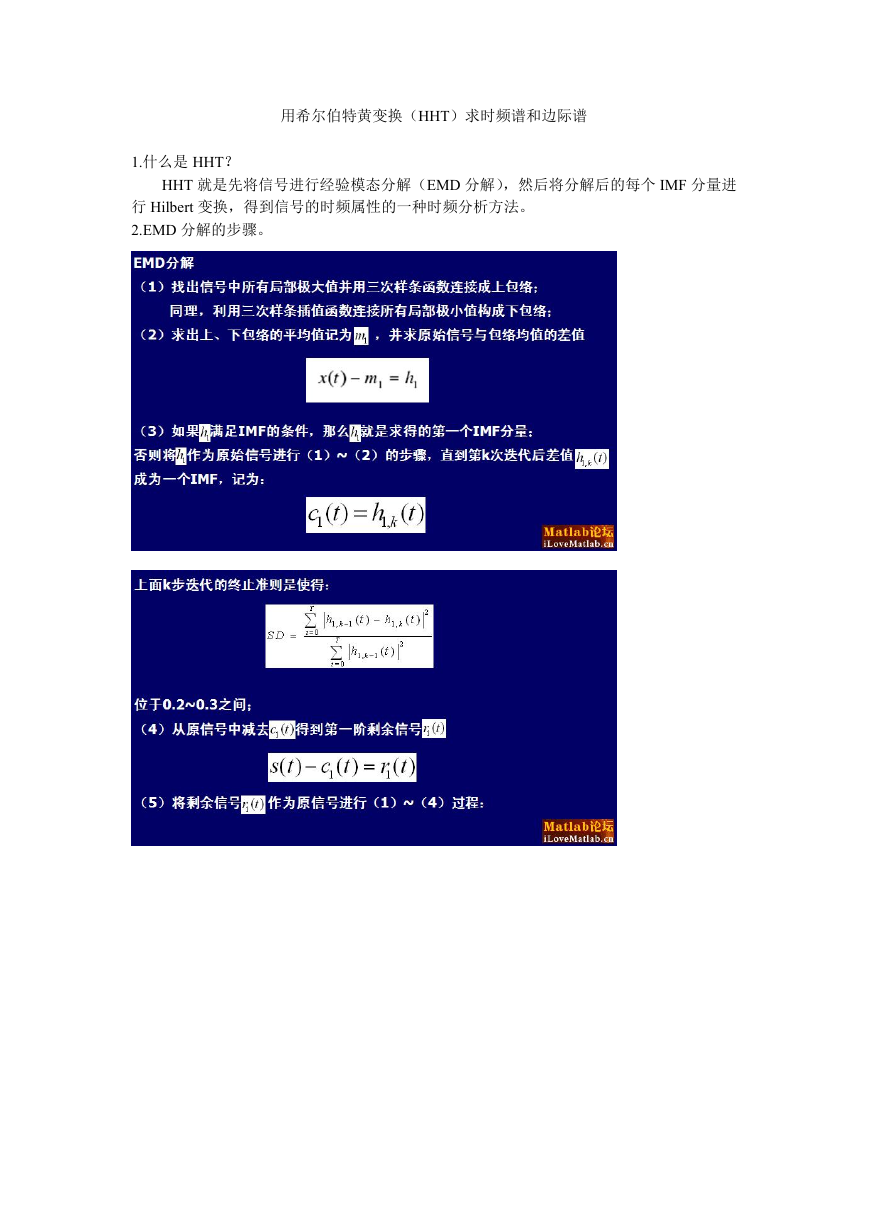
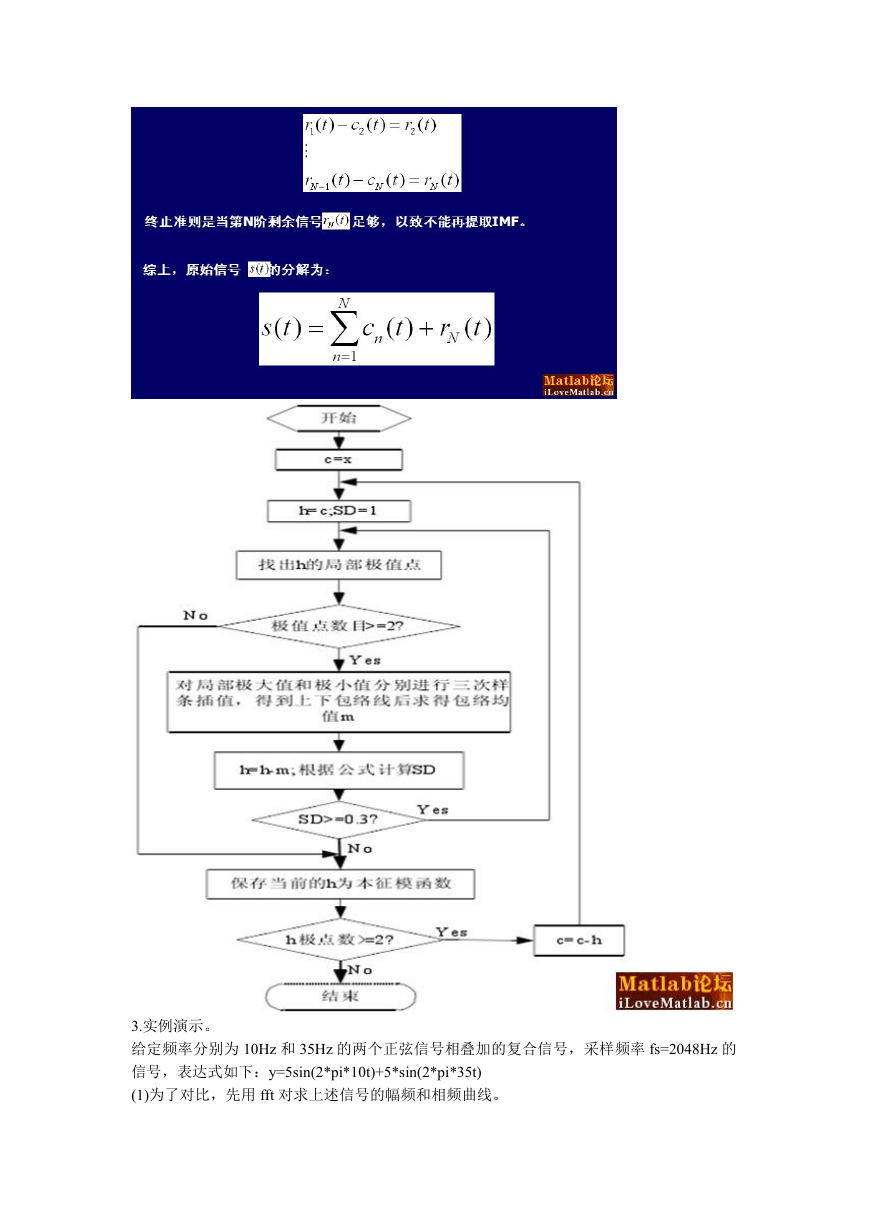
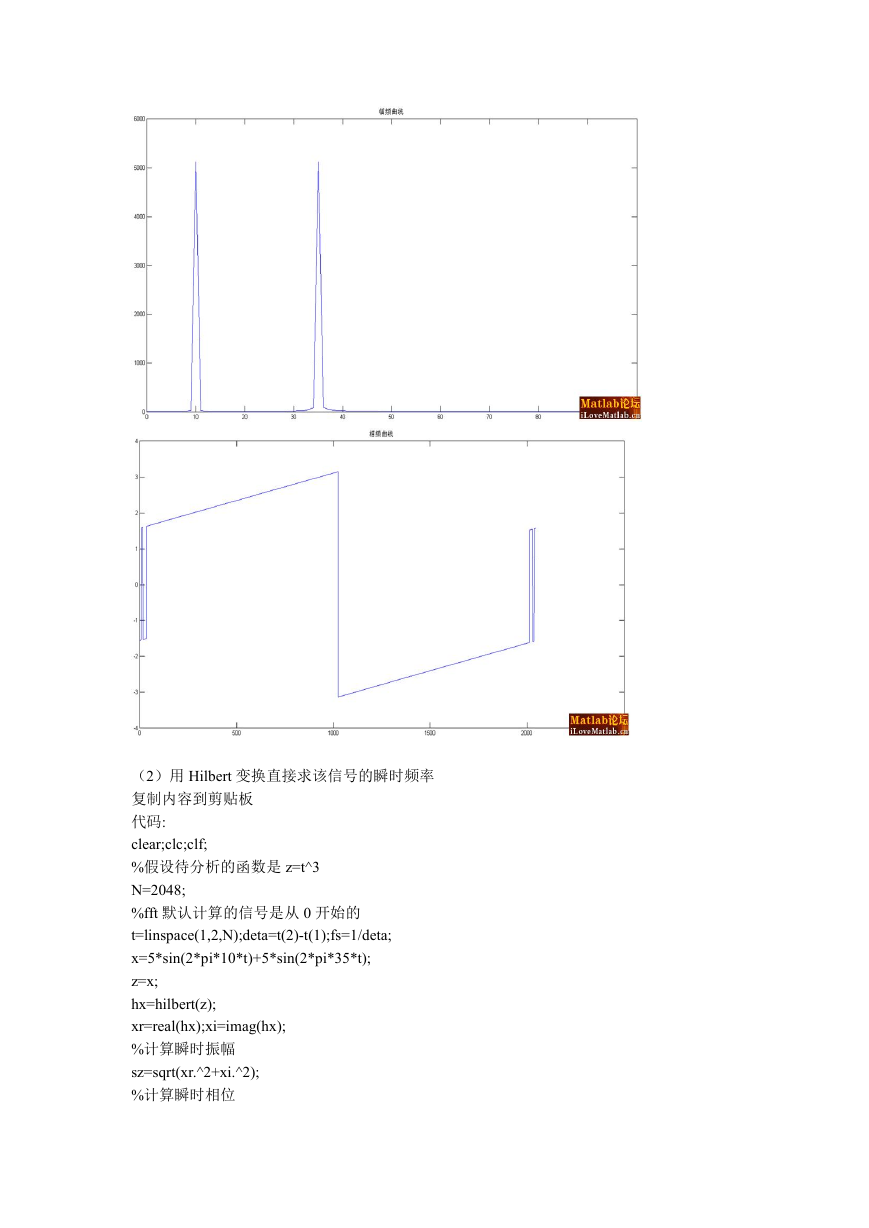
2.EMD 分解的步骤。
3.实例演示。
给定频率分别为 10Hz 和 35Hz 的两个正弦信号相叠加的复合信号，采样频率 fs=2048Hz 的
信号，表达式如下：y=5sin(2*pi*10t)+5*sin(2*pi*35t)
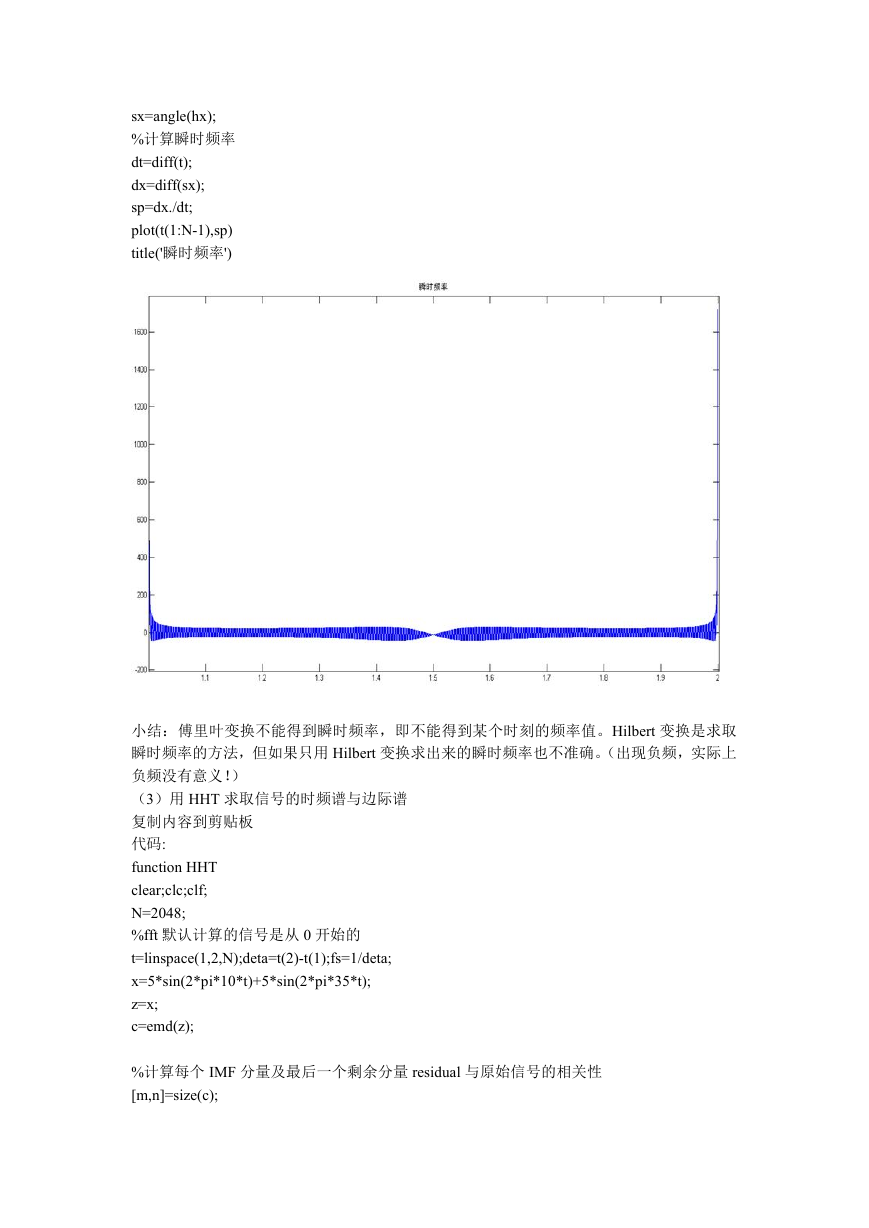
(1)为了对比，先用 fft 对求上述信号的幅频和相频曲线。
复制内容到剪贴板
代码:
function fftfenxi
clear;clc;
N=2048;
%fft 默认计算的信号是从 0 开始的
t=linspace(1,2,N);deta=t(2)-t(1);1/deta
x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);
% N1=256;N2=512;w1=0.2*2*pi;w2=0.3*2*pi;w3=0.4*2*pi;
%
x=(t>=-200&t<=-200+N1*deta).*sin(w1*t)+(t>-200+N1*deta&t<=-200+N2*deta).*sin(w2*t)+(t
>-200+N2*deta&t<=200).*sin(w3*t);
y = x;
m=0:N-1;
f=1./(N*deta)*m;%可以查看课本就是这样定义横坐标频率范围的
%下面计算的 Y 就是 x(t)的傅里叶变换数值
%Y=exp(i*4*pi*f).*fft(y)%将计算出来的频谱乘以 exp(i*4*pi*f)得到频移后[-2,2]之间的频谱
值
Y=fft(y);
z=sqrt(Y.*conj(Y));
plot(f(1:100),z(1:100));
title('幅频曲线')
xiangwei=angle(Y);
figure(2)
plot(f,xiangwei)
title('相频曲线')
figure(3)
plot(t,y,'r')
%axis([-2,2,0,1.2])
title('原始信号')
（2）用 Hilbert 变换直接求该信号的瞬时频率
复制内容到剪贴板
代码:
clear;clc;clf;
%假设待分析的函数是 z=t^3
N=2048;
%fft 默认计算的信号是从 0 开始的
t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;
x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);
z=x;
hx=hilbert(z);
xr=real(hx);xi=imag(hx);
%计算瞬时振幅
sz=sqrt(xr.^2+xi.^2);
%计算瞬时相位
sx=angle(hx);
%计算瞬时频率
dt=diff(t);
dx=diff(sx);
sp=dx./dt;
plot(t(1:N-1),sp)
title('瞬时频率')
小结：傅里叶变换不能得到瞬时频率，即不能得到某个时刻的频率值。Hilbert 变换是求取
瞬时频率的方法，但如果只用 Hilbert 变换求出来的瞬时频率也不准确。（出现负频，实际上
负频没有意义！）
（3）用 HHT 求取信号的时频谱与边际谱
复制内容到剪贴板
代码:
function HHT
clear;clc;clf;
N=2048;
%fft 默认计算的信号是从 0 开始的
t=linspace(1,2,N);deta=t(2)-t(1);fs=1/deta;
x=5*sin(2*pi*10*t)+5*sin(2*pi*35*t);
z=x;
c=emd(z);
%计算每个 IMF 分量及最后一个剩余分量 residual 与原始信号的相关性
[m,n]=size(c);
for i=1:m;
a=corrcoef(c(i,:),z);
xg(i)=a(1,2);
end
xg;
for i=1:m-1
%--------------------------------------------------------------------
%计算各 IMF 的方差贡献率
%定义：方差为平方的均值减去均值的平方
%均值的平方
%imfp2=mean(c(i,:),2).^2
%平方的均值
%imf2p=mean(c(i,:).^2,2)
%各个 IMF 的方差
mse(i)=mean(c(i,:).^2,2)-mean(c(i,:),2).^2;
end;
mmse=sum(mse);
for i=1:m-1
mse(i)=mean(c(i,:).^2,2)-mean(c(i,:),2).^2;
%方差百分比，也就是方差贡献率
mseb(i)=mse(i)/mmse*100;
%显示各个 IMF 的方差和贡献率
end;
%画出每个 IMF 分量及最后一个剩余分量 residual 的图形
figure(1)
for i=1:m-1
disp(['imf',int2str(i)]) ;disp([mse(i) mseb(i)]);
end;
subplot(m+1,1,1)
plot(t,z)
set(gca,'fontname','times New Roman')
set(gca,'fontsize',14.0)
ylabel(['signal','Amplitude'])
for i=1:m-1
subplot(m+1,1,i+1);
set(gcf,'color','w')
plot(t,c(i,:),'k')
set(gca,'fontname','times New Roman')
set(gca,'fontsize',14.0)
ylabel(['imf',int2str(i)])
end
subplot(m+1,1,m+1);
set(gcf,'color','w')
plot(t,c(m,:),'k')
set(gca,'fontname','times New Roman')
set(gca,'fontsize',14.0)
ylabel(['r',int2str(m-1)])
%画出每个 IMF 分量及剩余分量 residual 的幅频曲线
figure(2)
subplot(m+1,1,1)
set(gcf,'color','w')
[f,z]=fftfenxi(t,z);
plot(f,z,'k')
set(gca,'fontname','times New Roman')
set(gca,'fontsize',14.0)
ylabel(['initial signal',int2str(m-1),'Amplitude'])
for i=1:m-1
subplot(m+1,1,i+1);
set(gcf,'color','w')
[f,z]=fftfenxi(t,c(i,:));
plot(f,z,'k')
set(gca,'fontname','times New Roman')
set(gca,'fontsize',14.0)
ylabel(['imf',int2str(i),'Amplitude'])
end
subplot(m+1,1,m+1);
set(gcf,'color','w')
[f,z]=fftfenxi(t,c(m,:));
plot(f,z,'k')
set(gca,'fontname','times New Roman')
set(gca,'fontsize',14.0)
ylabel(['r',int2str(m-1),'Amplitude'])
hx=hilbert(z);
xr=real(hx);xi=imag(hx);
%计算瞬时振幅
sz=sqrt(xr.^2+xi.^2);
%计算瞬时相位
sx=angle(hx);
%计算瞬时频率
dt=diff(t);
dx=diff(sx);
sp=dx./dt;
figure(6)
plot(t(1:N-1),sp)
title('瞬时频率')
%计算 HHT 时频谱和边际谱
[A,fa,tt]=hhspectrum(c);
[E,tt1]=toimage(A,fa,tt,length(tt));
figure(3)
disp_hhs(E,tt1) %二维图显示 HHT 时频谱，E 是求得的 HHT 谱
pause
figure(4)
for i=1:size(c,1)
faa=fa(i,:);
[FA,TT1]=meshgrid(faa,tt1);%三维图显示 HHT 时频图
surf(FA,TT1,E)
title('HHT 时频谱三维显示')
hold on
end
hold off
E=flipud(E);
for k=1:size(E,1)
bjp(k)=sum(E(k,:))*1/fs;
end
f=(1:N-2)/N*(fs/2);
figure(5)
plot(f,bjp);
xlabel('频率 / Hz');
ylabel('信号幅值');
title('信号边际谱')%要求边际谱必须先对信号进行 EMD 分解
function [A,f,tt] = hhspectrum(x,t,l,aff)
error(nargchk(1,4,nargin));
if nargin < 2
t=1:size(x,2);
end
if nargin < 3
l=1;
end
if nargin < 4
aff = 0;
end
if min(size(x)) == 1
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
