利用MATLAB曲线拟合工具箱求离散点的拟合曲线.pdf-资料库

中国科技论文在线 http://www.paper.edu.cn 利用 MATLAB 曲线拟合工具箱求离散点的拟合曲线陈巍* （辽宁工程技术大学理学院，辽宁阜新 123000）摘要：曲线拟合是数值分析中的一种普遍且重要的方法，求解拟合曲线的方法也有很多.本文主要介绍利用 MATLAB 曲线拟合工具箱对离散数据点做拟合处理，并与利用最小二乘法求相应的拟合曲线的方法做对比，突出 MATLAB 曲线拟合工具箱的优点，并阐述了其适用范围.最后通过利用 MATLAB 曲线拟合工具箱对实例中离散数据的拟合来具体说明它的使用方法和优点. 关键词：数值分析；MATLAB；曲线拟合；最小二乘法中图分类号：O241 Utilize the curve-fitting toolbox of MATLAB to seek fitted curve of some disciete points Chen Wei (Liaoning Technical University College of Science,Liaoning Fuxin 123000) Abstract: Curve fitting is a common and important method in numerical analysis and there are a lot of approaches for solving fitted curve .This paper mainly introduce the method that utilize the Curve- Fitting Toolbox of MATLAB to fit some discrete data points and contrast with the method of the minimum squares. Through the contrast, it highlight the advantage of MATLAB Curve-Fitting Toolbox and elaborate its scope. At last, this paper specify the usage and the advantage of MATLAB Curve- Fitting Toolbox by example. Key words: numerical analysis; MATLAB; Curve-Fitting; minimum squares 0 引言在很多实际情况中，两个变量之间的关系往往很难用具体的表达式把它表示出来，通常只能通过实际测量得到一些互不相同的离散数据点.需要利用这些已知的数据点估计出两个变量的关系或工件的具体轮廓，并要得到任意未知数据点的具体数值，这个过程就需要用到拟合或差值方法来实现.本文主要讨论拟合的方法. 曲线拟合可以通过 MATLAB 编程来完成，通常为了达到更好的拟合效果需要做多次重复修改，对于非线性曲线拟合还需要编写复杂的 M-文件.运用 MATLAB 曲线拟合工具箱来实现离散数据点的曲线拟合是一种直观并且简洁的方法. 1 曲线拟合的最小二乘法理论假设给定了一些数据点( )ii yx , ,人们总希望能找到这样的近似函数，它既能反映所给数据的一般趋势，又不会出现较大偏差，并且要使构造的函数与被逼近函数在一个给定区间上的偏差满足某种要求.这种思想就是所谓的“曲线拟合”的思想. 曲线拟合和差值不同，若要求通过所有给定的数据点是差值问题，若不要求曲线通过所有给定的数据点，而只是要求它反映对象整体的变化趋势，这就是拟合问题.曲线拟合问题作者简介：陈巍（1985-），女，硕士研究生，主要研究方向：最优化理论. E-mail: weiweichen_5566@126.com - 1 -

中国科技论文在线 http://www.paper.edu.cn 最常用的解法是线性最小二乘法[1]，步骤如下： ( ) ( ) < 第一步：先选定一组函数 nmxr , xrxr , 1 ( ) ( ) ( )xra + mm+ = xraxraxf ( ) , + , 2 ( ) 1 为待定系数. aa ,, 2 其中第二步：确定的准则（最小二乘准则）：使n个点( )i i yx , ma , 22 11 m ，令：与曲线 ( )xfy = 的距离 iδ 的平方和最小.记 ( aaJ 2 ,, 1 a , m n n ) = = 2 i δ ∑ [ ( ∑ xf i 1 使 ( aa ,, 2 ma , = i = i 1 1 1 ,, 2 aaJ ) − 2 y i ] )ma , = m n ∑ ∑ = i 1 = k 1 ⎡ ⎢ ⎣ ( xra ikk ) − 2 y i ⎤ ⎥ ⎦ 问题归结为，求最小二乘法中如何选择数学模型很重要。用 MATLAB 解决曲线拟合问题通常有两种方法：线性最小二乘拟合和非线性最小二乘拟合.对于两种方法的选择，要根据离散数据点位置关系来确定，即首先将数据( = n , 最小. 作图，通过直观判断确定. axa m + + m 1 + + 拟合.可利用已有 iyx ii 线性最小二乘法通常是做多项式 ( ) a , ,2,1 ) , m xaxf = 1 的程序 y = = ( )myx ployfit ,, ( )xa 计算.做非线性最小二乘拟合时，应首先选择好适当的数学模型，如 , ployval 其中 m代表拟合多项式的次数.多项式在x 处 y 的值可用命令 + ，令 Y ln= bxae = ln ，其中 ba, 为待定参数.此时可以把它转化成线性模型来计算，两边取对数得 = ,求这个线性模型的 bxa lsqcurvefi 和lsqnonlin mfun. ，在其中定义函数 ( )xf ，但两者定义 M-文件的 y = ln y 最小二乘问题.另外一种方法就是直接采用非线性拟合的函数来计算.两个命令都要先建立 M-文件方式有所不同. bxAY A ln= ,于是有 ,记 t y a + 这些问题同样可以用 MATLAB 拟合工具[2]箱来实现，并且操作比较简单，误差等参数也能一目了然的观察到. 2 MATLAB 曲线拟合工具箱 MATLAB 曲线拟合工具箱界面[3]是一个可视化的图形界面，具有强大的图形拟合功能，其中包括：（1）可视化的展开一个或多个数据集，并可用散点图来表示；（2）用残差和置信区间可视化的估计拟合结果的好坏；（3）通过其他界面还可以实现许多其他功能：比如输出、查看和平滑数据；拟合数据，比较拟合曲线和数据集；从拟合曲线中排除特殊的数据点；选定区间后可以显示拟合曲线和数据集.它把计算，可视化和程序设计融合到一个交互的环境，在此环境中，利用强大的数值计算和图形功能，可高效求解一些复杂的工程问题及实现计算结果的可视化. 用 MATLAB 曲线拟合工具箱对离散数据进行拟合时，可使用 MATLAB 内部的库函数或用户自定义的方程对参变量进行多项式、指数、有理数等形式的数据拟合. 3 MATLAB 曲线拟合工具箱的应用举例在实际中，产品和工件的轮廓形状很难找到一个具体的数学表达式，通常只能通过实验或数学计算得到一些离散点及其上的数值点.此时就需要选择合适的数学模型对其进行曲线 - 2 -

中国科技论文在线 http://www.paper.edu.cn 拟合，做出它的拟合曲线，从而估计出它的实际形状.下面通过一个例子说明一下用 MATLAB 曲线拟合工具箱对离散数据点进行曲线拟合，并与一般方法的比较. 例1 已知机翼下轮廓上的数据如下表所示：表 1[4] 机翼下轮廓数据 Tab. 1 under profile datum of airfoil 机翼长（X） 0 3 5 7 9 11 12 13 14 15 机翼宽（Y） 0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.4 1.6 用这些数据拟合轮廓形状. 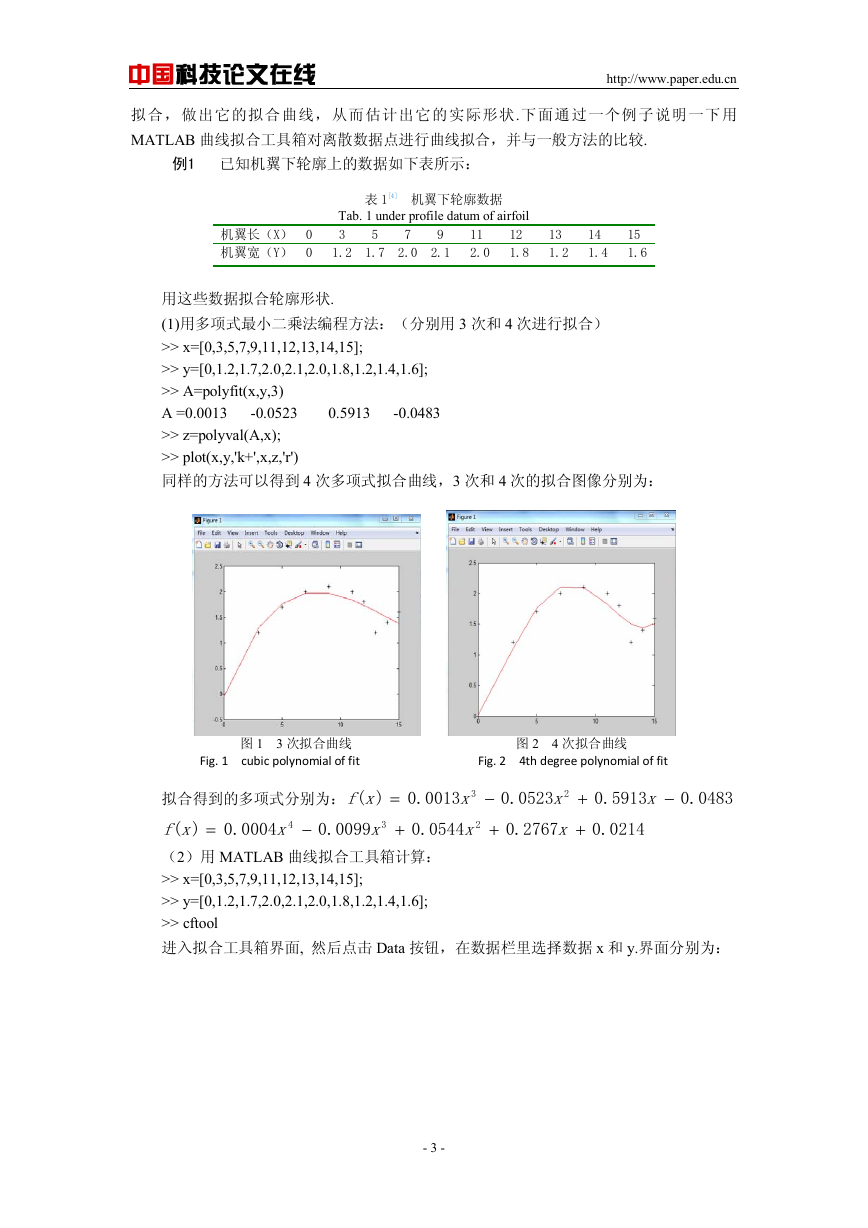(1)用多项式最小二乘法编程方法：（分别用 3 次和 4 次进行拟合） >> x=[0,3,5,7,9,11,12,13,14,15]; >> y=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.4,1.6]; >> A=polyfit(x,y,3) A =0.0013 -0.0523 0.5913 -0.0483 >> z=polyval(A,x); >> plot(x,y,'k+',x,z,'r') 同样的方法可以得到 4 次多项式拟合曲线，3 次和 4 次的拟合图像分别为：图 1 3 次拟合曲线图 2 4 次拟合曲线 Fig. 1 cubic polynomial of fit Fig. 2 4th degree polynomial of fit 0013 3 x .0 = + − + .0 + + 拟合得到的多项式分别为： )( xf .0 0523 2 x .0 5913 x − .0 0483 = − .0 3 x 2 x .0 0004 4 x .0 0099 0544 )( xf （2）用 MATLAB 曲线拟合工具箱计算： >> x=[0,3,5,7,9,11,12,13,14,15]; >> y=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.4,1.6]; >> cftool 进入拟合工具箱界面, 然后点击 Data 按钮，在数据栏里选择数据 x 和 y.界面分别为： 0214 2767 x .0 - 3 -

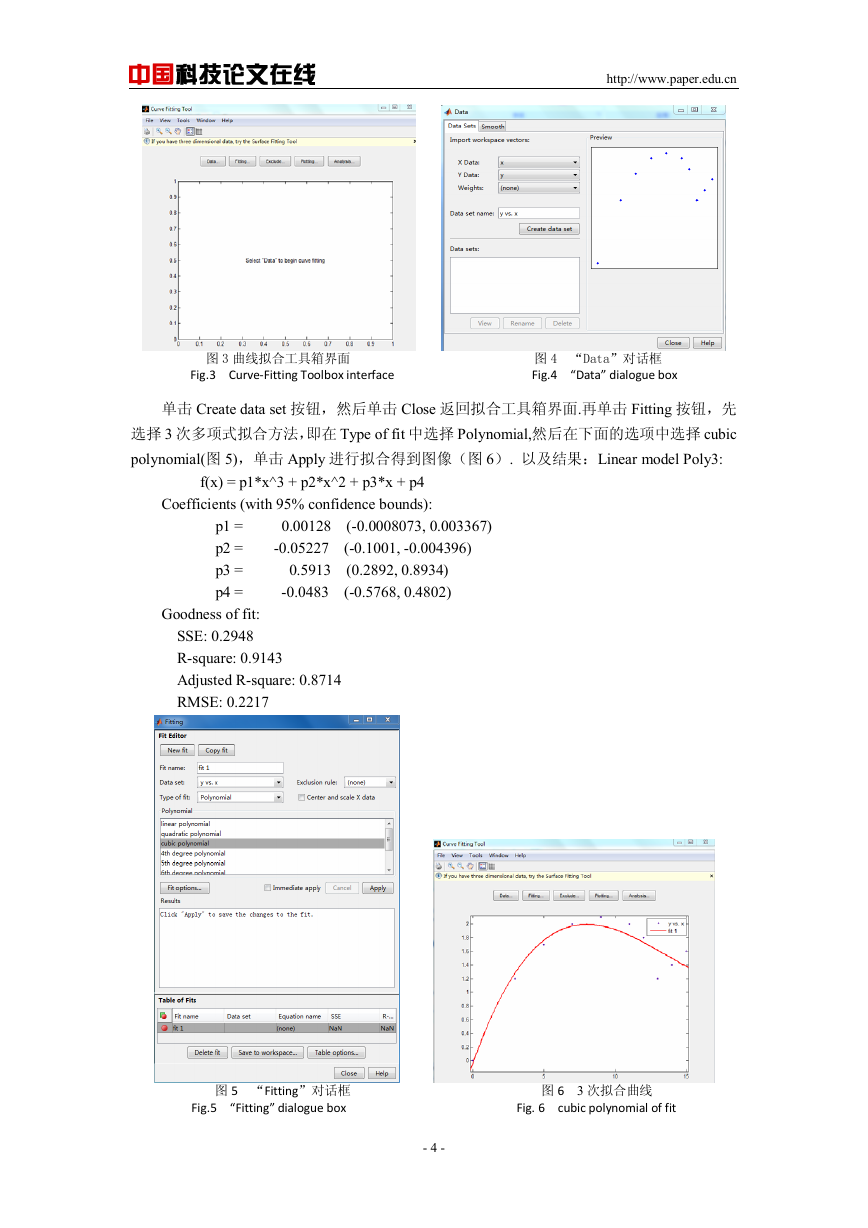
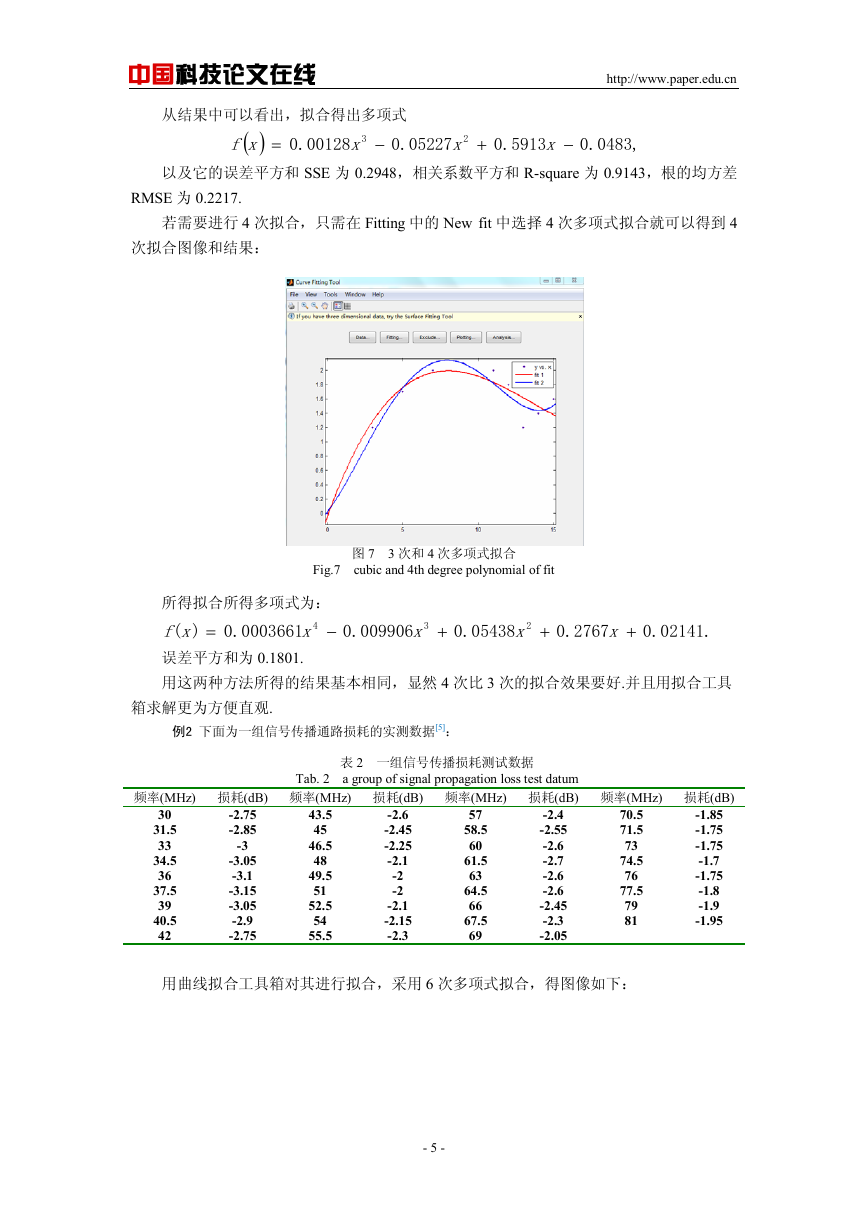
中国科技论文在线 http://www.paper.edu.cn 图 3 曲线拟合工具箱界面图 4 “Data”对话框 Fig.3 Curve‐Fitting Toolbox interface Fig.4 “Data” dialogue box 单击 Create data set 按钮，然后单击 Close 返回拟合工具箱界面.再单击 Fitting 按钮，先选择 3 次多项式拟合方法，即在 Type of fit 中选择 Polynomial,然后在下面的选项中选择 cubic polynomial(图 5)，单击 Apply 进行拟合得到图像（图 6）. 以及结果：Linear model Poly3: f(x) = p1*x^3 + p2*x^2 + p3*x + p4 Coefficients (with 95% confidence bounds): p1 = 0.00128 (-0.0008073, 0.003367) p2 = -0.05227 (-0.1001, -0.004396) p3 = 0.5913 (0.2892, 0.8934) p4 = -0.0483 (-0.5768, 0.4802) Goodness of fit: SSE: 0.2948 R-square: 0.9143 Adjusted R-square: 0.8714 RMSE: 0.2217 图 5 “Fitting”对话框图 6 3 次拟合曲线 Fig.5 “Fitting” dialogue box Fig. 6 cubic polynomial of fit - 4 -

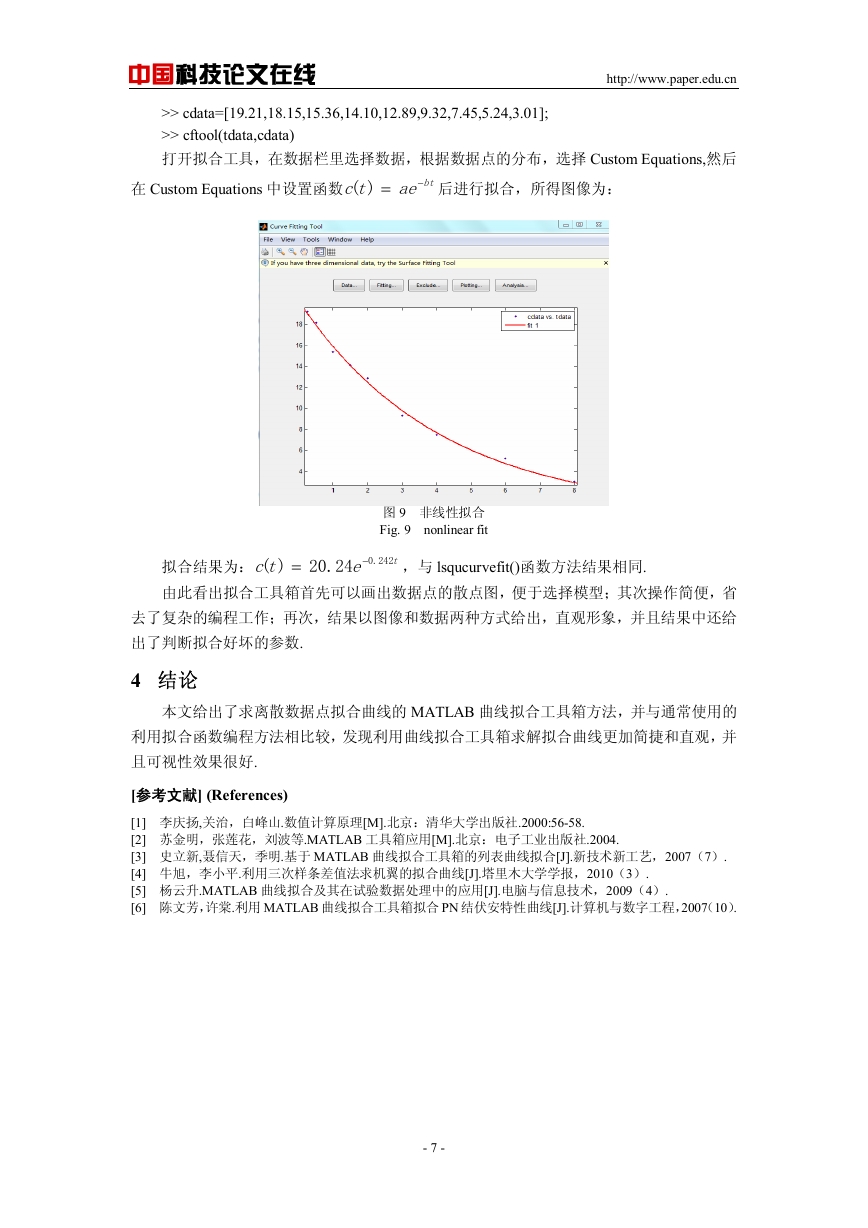
中国科技论文在线 http://www.paper.edu.cn 从结果中可以看出，拟合得出多项式 ( ) xf = .0 00128 3 x − .0 05227 2 x + .0 5913 x − .0 , 0483 以及它的误差平方和 SSE 为 0.2948，相关系数平方和 R-square 为 0.9143，根的均方差 RMSE 为 0.2217. 若需要进行 4 次拟合，只需在 Fitting 中的 New fit 中选择 4 次多项式拟合就可以得到 4 次拟合图像和结果：图 7 3 次和 4 次多项式拟合 Fig.7 cubic and 4th degree polynomial of fit + 所得拟合所得多项式为： − .0 = 4 0003661 )( x xf 误差平方和为 0.1801. 用这两种方法所得的结果基本相同，显然 4 次比 3 次的拟合效果要好.并且用拟合工具 009906 . 02141 05438 2767 2 x 3 x .0 .0 .0 .0 x + + 箱求解更为方便直观. 例2 下面为一组信号传播通路损耗的实测数据[5]：表 2 一组信号传播损耗测试数据 Tab. 2 a group of signal propagation loss test datum -2.75 -2.85 -3 -3.05 -3.1 -3.15 -3.05 -2.9 -2.75 频率(MHz) 损耗(dB) 频率(MHz) 损耗(dB) 频率(MHz) 损耗(dB) 频率(MHz) 损耗(dB) -1.85 -1.75 -1.75 -1.7 -1.75 -1.8 -1.9 -1.95 30 31.5 33 34.5 36 37.5 39 40.5 42 用曲线拟合工具箱对其进行拟合，采用 6 次多项式拟合，得图像如下： -2.6 -2.45 -2.25 -2.1 -2 -2 -2.1 -2.15 -2.3 -2.4 -2.55 -2.6 -2.7 -2.6 -2.6 -2.45 -2.3 -2.05 43.5 45 46.5 48 49.5 51 52.5 54 55.5 57 58.5 60 61.5 63 64.5 66 67.5 69 70.5 71.5 73 74.5 76 77.5 79 81 - 5 -

中国科技论文在线 http://www.paper.edu.cn 图 8 6 次多项式拟合 Fig. 8 6th degree polynomial of fit 下面再举一个非线性拟合的例子. 例 3 用非线性拟合[6]的方法对下列一组数据进行拟合：表 3 快速静脉注射下的血药浓度数据 Tab. 3 blood concentration datum under rapid intravenous injection t(h) c( 0.25 19.21 0.5 18.15 1 1.5 14.10 2 3 9.32 4 7.45 6 5.24 8 3.01 = − 15.36 12.98 btae ,其中， ba, 是待定参数. ml g /µ ) 根据数据特点，选取数学模型： ( ) tc （1）用 lsqucurvefit()函数做拟合：编写 M-文件：function f=curvefun1(x,tdata) f=x(1)*exp(-x(2)*tdata 输入程序：tdata=[0.25,0.5,1,1.5,2,3,4,6,8]; >> cdata=[19.21,18.15,15.36,14.10,12.89,9.32,7.45,5.24,3.01]; >> x0=[20,0.1]; >> x0=[0.2,0.05,0.05]; x=lsqcurvefit ('curvefun1',x0,tdata,cdata) f= curvefun1(x,tdata) x = 20.2413 0.2420 f =19.0532 17.9348 15.8911 14.0802 12.4757 9.7945 7.6894 4.7394 2.9211 f = 19.0532 17.9348 15.8911 14.0802 12.4757 9.7945 7.6894 4.7394 2.9211 = − e .0 2420 t .20 )( tc 2413 即（2）用拟合工具箱计算：输入程序： >> tdata=[0.25,0.5,1,1.5,2,3,4,6,8]; - 6 -

中国科技论文在线 http://www.paper.edu.cn >> cdata=[19.21,18.15,15.36,14.10,12.89,9.32,7.45,5.24,3.01]; >> cftool(tdata,cdata) 打开拟合工具，在数据栏里选择数据，根据数据点的分布，选择 Custom Equations,然后在 Custom Equations 中设置函数 =)( tc 后进行拟合，所得图像为： − btae 图 9 非线性拟合 Fig. 9 nonlinear fit 拟合结果为： )( tc = 24.20 − .0 242 te ，与 lsqucurvefit()函数方法结果相同. 由此看出拟合工具箱首先可以画出数据点的散点图，便于选择模型；其次操作简便，省去了复杂的编程工作；再次，结果以图像和数据两种方式给出，直观形象，并且结果中还给出了判断拟合好坏的参数. 4 结论本文给出了求离散数据点拟合曲线的 MATLAB 曲线拟合工具箱方法，并与通常使用的利用拟合函数编程方法相比较，发现利用曲线拟合工具箱求解拟合曲线更加简捷和直观，并且可视性效果很好. [参考文献] (References) [1] 李庆扬,关治，白峰山.数值计算原理[M].北京：清华大学出版社.2000:56-58. [2] 苏金明，张莲花，刘波等.MATLAB 工具箱应用[M].北京：电子工业出版社.2004. [3] 史立新,聂信天，季明.基于 MATLAB 曲线拟合工具箱的列表曲线拟合[J].新技术新工艺，2007（7）. [4] 牛旭，李小平.利用三次样条差值法求机翼的拟合曲线[J].塔里木大学学报，2010（3）. [5] 杨云升.MATLAB 曲线拟合及其在试验数据处理中的应用[J].电脑与信息技术，2009（4）. [6] 陈文芳，许棠.利用 MATLAB 曲线拟合工具箱拟合 PN 结伏安特性曲线[J].计算机与数字工程，2007（10）. - 7 -

资料库

利用MATLAB曲线拟合工具箱求离散点的拟合曲线.pdf

相关推荐

开发技术

热门标签

最新资料