第1页 / 共22页
第2页 / 共22页
第3页 / 共22页
第4页 / 共22页
第5页 / 共22页
第6页 / 共22页
第7页 / 共22页
第8页 / 共22页
Grandmaster level in StarCraft II using.pdf
Grandmaster level in StarCraft II using multi-agent reinforcement learning
Learning algorithm
Empirical evaluation
Conclusion
Online content
Fig. 1 Training setup.
Fig. 2 Results.
Fig. 3 Ablations for key components of AlphaStar.
Fig. 4 AlphaStar training progression.
Extended Data Fig. 1 APM limits.
Extended Data Fig. 2 Delays.
Extended Data Fig. 3 Overview of the architecture of AlphaStar.
Extended Data Fig. 4 Distribution of units built in a game.
Extended Data Fig. 5 A more detailed analysis of multi-agent ablations from Fig.
Extended Data Fig. 6 Training infrastructure.
Extended Data Fig. 7 Battle.
Extended Data Fig. 8 Payoff matrix (limited to only Protoss versus Protoss games for simplicity) split into agent types of the league.
Extended Data Table 1 Agent input space.
Extended Data Table 2 Agent action space.
Grandmaster level in StarCraft II using
multi-agent reinforcement learning
https://doi.org/10.1038/s41586-019-1724-z
Received: 30 August 2019
Accepted: 10 October 2019
Published online: 30 October 2019
Oriol Vinyals1,3*, Igor Babuschkin1,3, Wojciech M. Czarnecki1,3, Michaël Mathieu1,3,
Andrew Dudzik1,3, Junyoung Chung1,3, David H. Choi1,3, Richard Powell1,3, Timo Ewalds1,3,
Petko Georgiev1,3, Junhyuk Oh1,3, Dan Horgan1,3, Manuel Kroiss1,3, Ivo Danihelka1,3,
Aja Huang1,3, Laurent Sifre1,3, Trevor Cai1,3, John P. Agapiou1,3, Max Jaderberg1,
Alexander S. Vezhnevets1, Rémi Leblond1, Tobias Pohlen1, Valentin Dalibard1, David Budden1,
Yury Sulsky1, James Molloy1, Tom L. Paine1, Caglar Gulcehre1, Ziyu Wang1, Tobias Pfaff1,
Yuhuai Wu1, Roman Ring1, Dani Yogatama1, Dario Wünsch2, Katrina McKinney1, Oliver Smith1,
Tom Schaul1, Timothy Lillicrap1, Koray Kavukcuoglu1, Demis Hassabis1, Chris Apps1,3 &
David Silver1,3*
Many real-world applications require artificial agents to compete and coordinate
with other agents in complex environments. As a stepping stone to this goal, the
domain of StarCraft has emerged as an important challenge for artificial intelligence
research, owing to its iconic and enduring status among the most difficult
professional esports and its relevance to the real world in terms of its raw complexity
and multi-agent challenges. Over the course of a decade and numerous
competitions1–3, the strongest agents have simplified important aspects of the game,
utilized superhuman capabilities, or employed hand-crafted sub-systems4. Despite
these advantages, no previous agent has come close to matching the overall skill of
top StarCraft players. We chose to address the challenge of StarCraft using general-
purpose learning methods that are in principle applicable to other complex
domains: a multi-agent reinforcement learning algorithm that uses data from both
human and agent games within a diverse league of continually adapting strategies
and counter-strategies, each represented by deep neural networks5,6. We evaluated
our agent, AlphaStar, in the full game of StarCraft II, through a series of online games
against human players. AlphaStar was rated at Grandmaster level for all three
StarCraft races and above 99.8% of officially ranked human players.
StarCraft is a real-time strategy game in which players balance high-
level economic decisions with individual control of hundreds of units.
This domain raises important game-theoretic challenges: it features a
vast space of cyclic, non-transitive strategies and counter-strate-
gies; discovering novel strategies is intractable with naive self-play
exploration methods; and those strategies may not be effective when
deployed in real-world play with humans. Furthermore, StarCraft
has a combinatorial action space, a planning horizon that extends
over thousands of real-time decisions, and imperfect information7.
Each game consists of tens of thousands of time-steps and thousands
of actions, selected in real-time throughout approximately ten minutes
of gameplay. At each step t, our agent AlphaStar receives an observation
ot that includes a list of all observable units and their attributes. This
information is imperfect; the game includes only opponent units seen
by the player’s own units, and excludes some opponent unit attributes
outside the camera view.
Each action at is highly structured: it selects what action type, out of
several hundred (for example, move or build worker); who to issue that
action to, for any subset of the agent’s units; where to target, among
locations on the map or units within the camera view; and when to
observe and act next (Fig. 1a). This representation of actions results
in approximately 1026 possible choices at each step. Similar to human
players, a special action is available to move the camera view, so as to
gather more information.
Humans play StarCraft under physical constraints that limit their
reaction time and the rate of their actions. The game was designed with
those limitations in mind, and removing those constraints changes the
nature of the game. We therefore chose to impose constraints upon
AlphaStar: it suffers from delays due to network latency and compu-
tation time; and its actions per minute (APM) are limited, with peak
statistics substantially lower than those of humans (Figs. 2c, 3g for
performance analysis). AlphaStar’s play with this interface and these
1DeepMind, London, UK. 2Team Liquid, Utrecht, Netherlands. 3These authors contributed equally: Oriol Vinyals, Igor Babuschkin, Wojciech M. Czarnecki, Michaël Mathieu, Andrew Dudzik,
Junyoung Chung, David H. Choi, Richard Powell, Timo Ewalds, Petko Georgiev, Junhyuk Oh, Dan Horgan, Manuel Kroiss, Ivo Danihelka, Aja Huang, Laurent Sifre, Trevor Cai, John P. Agapiou,
Chris Apps, David Silver. *e-mail: vinyals@google.com; davidsilver@google.com
Nature | www.nature.com | 1
Article
a
Monitoring layer
Actions limit ~22 per 5 s
Requested delay ~200 ms
Move
s
m
0
8
Action
Move
Attack
Build
What?
Who?
Where?
When next
action?
l
i
y
a
e
d
g
n
s
s
e
c
o
r
p
e
m
i
t
-
l
a
e
R
Own units
Minimap
Camera vision
Outside camera
Opponents units
Camera vision
?
Outside camera
b
Reinforcement learning
c
Supervised players
Past players
Current players
SL
t
L V - T r a
P
U
t
K
e
O
c
G
Rt
)
(
D
T
Vt
Fig. 1 | Training setup. a, AlphaStar observes the game
through an overview map and list of units. To act, the
agent outputs what action type to issue (for example,
build), who it is applied to, where it targets, and when
the next action will be issued. Actions are sent to the
game through a monitoring layer that limits action
rate. AlphaStar contends with delays from network
latency and processing time. b, AlphaStar is trained
via both supervised learning and reinforcement
learning. In supervised learning (bottom), the
parameters are updated to optimize Kullback–Leibler
(KL) divergence between its output and human
actions sampled from a collection of replays. In
reinforcement learning (top), human data are used to
sample the statistic z, and agent experience is
collected to update the policy and value outputs via
reinforcement learning (TD(λ), V-trace, UPGO)
combined with a KL loss towards the supervised
agent. c, Three pools of agents, each initialized by
supervised learning, were subsequently trained with
reinforcement learning. As they train, these agents
intermittently add copies of themselves—‘players’
that are frozen at a specific point—to the league. The
main agents train against all of these past players, as
well as themselves. The league exploiters train against
all past players. The main exploiters train against the
main agents. Main exploiters and league exploiters
can be reset to the supervised agent when they add a
player to the league. Images from StarCraft
reproduced with permission from Blizzard
Entertainment.
s
m
0
3
l
i
y
a
e
d
g
n
s
s
e
c
o
r
p
e
m
i
t
-
l
a
e
R
M
a
n
i
a
g
e
n
t
s
o߰t
ࢣrt+k
ot
H
u
m
a
n
d
a
t
a
Rewards
rp
t
rp
rT = ±1
Opponent
Agent
Human
z
Supervised learning
at
L
K
SL
t
ot
t
z
Human
M
a
n
i
l
e
x
p
o
i
t
e
r
s
L
e
a
g
u
e
e
x
p
o
i
t
e
r
s
l
Time
Matchmaking target
Reinforcement learning
Supervised learning
Reinitialization
Zerg
Terran
Protoss
constraints was approved by a professional player (see ‘Professional
player statement’ in Methods).
Learning algorithm
To address the complexity and game-theoretic challenges of StarCraft,
AlphaStar uses a combination of new and existing general-purpose
techniques for neural network architectures, imitation learning, rein-
forcement learning, and multi-agent learning. Further details about
these techniques are given in the Methods.
π a s z
(
θ
, represented
by a neural network with parameters θ that receives all observations
st = (o1:t, a1:t − 1) from the start of the game as inputs, and selects actions
as outputs. The policy is also conditioned on a statistic z that summa-
rizes a strategy sampled from human data (for example, a build order).
Our agent architecture consists of general-purpose neural network
components that handle StarCraft’s raw complexity. Observations of
Central to AlphaStar is a policy
ℙ
, ) = [
a s z
, ]
|
|
t
t
t
t
player and opponent units are processed using a self-attention mecha-
nism8. To integrate spatial and non-spatial information, we introduce
scatter connections. To deal with partial observability, the tempo-
ral sequence of observations is processed by a deep long short-term
memory (LSTM) system9. To manage the structured, combinatorial
action space, the agent uses an auto-regressive policy7,10,11 and recurrent
pointer network12. Extended Data Fig. 3 summarizes the architecture
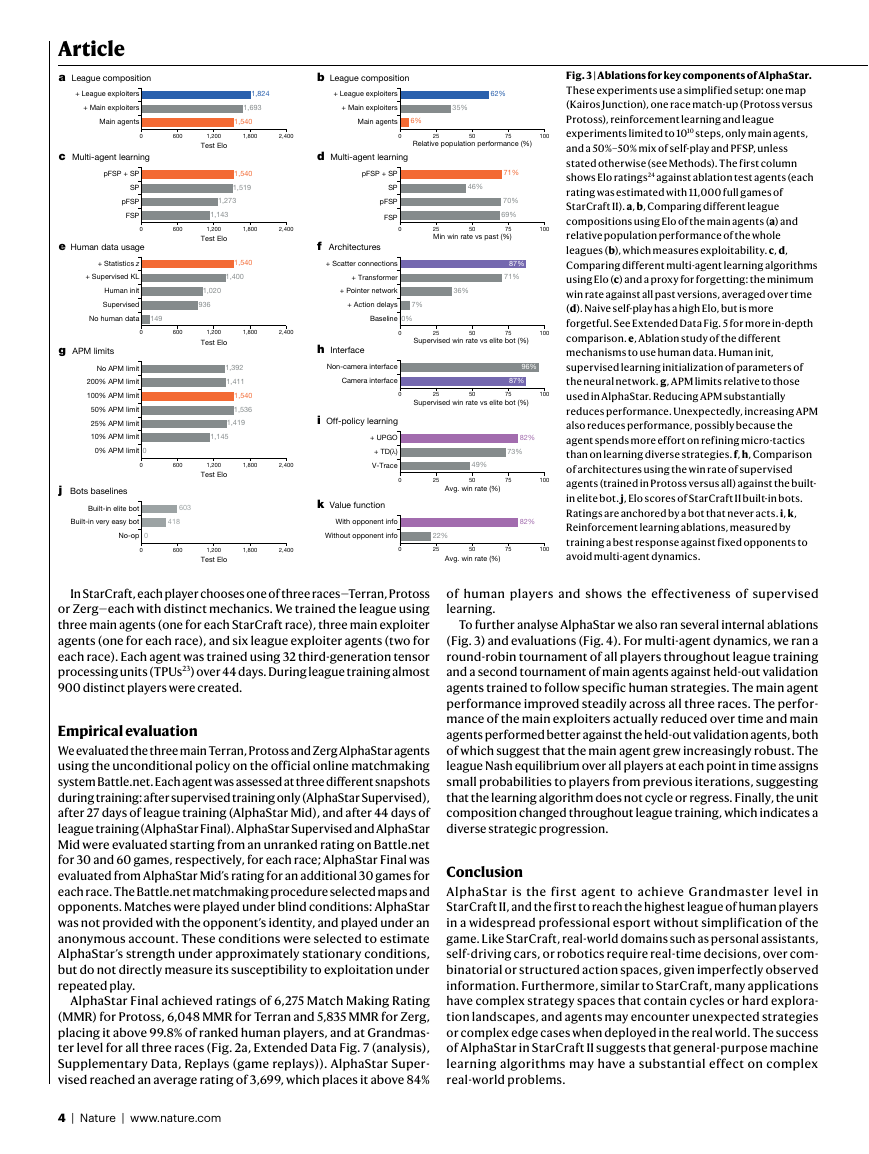
and Fig. 3f shows an ablation of each component.
Agent parameters were initially trained by supervised learning.
Games were sampled from a publicly available dataset of anonymized
human replays. The policy was then trained to predict each action at,
conditioned either solely on st, or also on z. This results in a diverse set
of strategies that reflects the modes of human play.
The agent parameters were subsequently trained by a reinforcement
learning algorithm that is designed to maximize the win rate (that is,
compute a best response) against a mixture of opponents. The choice
of opponent is determined by a multi-agent procedure, described
2 | Nature | www.nature.com
Article
a
7,000
6,000
5,000
R
M
M
4,000
3,000
2,000
1,000
e
z
n
o
r
B
0
0
7,000
6,500
6,000
5,500
5,000
AlphaStar Final
AlphaStar Mid
Master
GM
98.5
98.9
99.2
99.6
100.0
r
e
v
l
i
S
l
d
o
G
m
u
n
i
t
a
P
l
d
n
o
m
a
D
i
r
e
t
s
a
M
AlphaStar Final
AlphaStar Mid
AlphaStar Supervised
r
e
t
s
a
m
d
n
a
r
G
25
50
Percentile
75
100
b
e
c
a
r
r
a
t
S
a
h
p
A
l
Opponent race
c
6,275
99.93%
25/30
6,196
99.91%
11/14
–
–
4/4
6,048
99.86%
18/30
5,991
99.83%
4/8
6,209
99.92%
4/7
5,835
99.76%
18/30
5,755
99.7%
8/14
5,531
99.51%
5/10
6,297
99.94%
10/12
5,971
99.82%
10/15
6,500
99.96%
5/6
0.05
0.04
0.03
0.02
0.01
y
t
i
l
i
b
a
b
o
r
P
0
0
Terran
Avg 99.9% Max
571
183
174
873
487
671
Protoss
Avg 99.9% Max
503
187
587
165
739 1,814
Zerg
Avg 99.9% Max
211
823
205 1,259 4,166
655
300
600
900
0
300
600
900
0
300
600
900
EPM
EPM
EPM
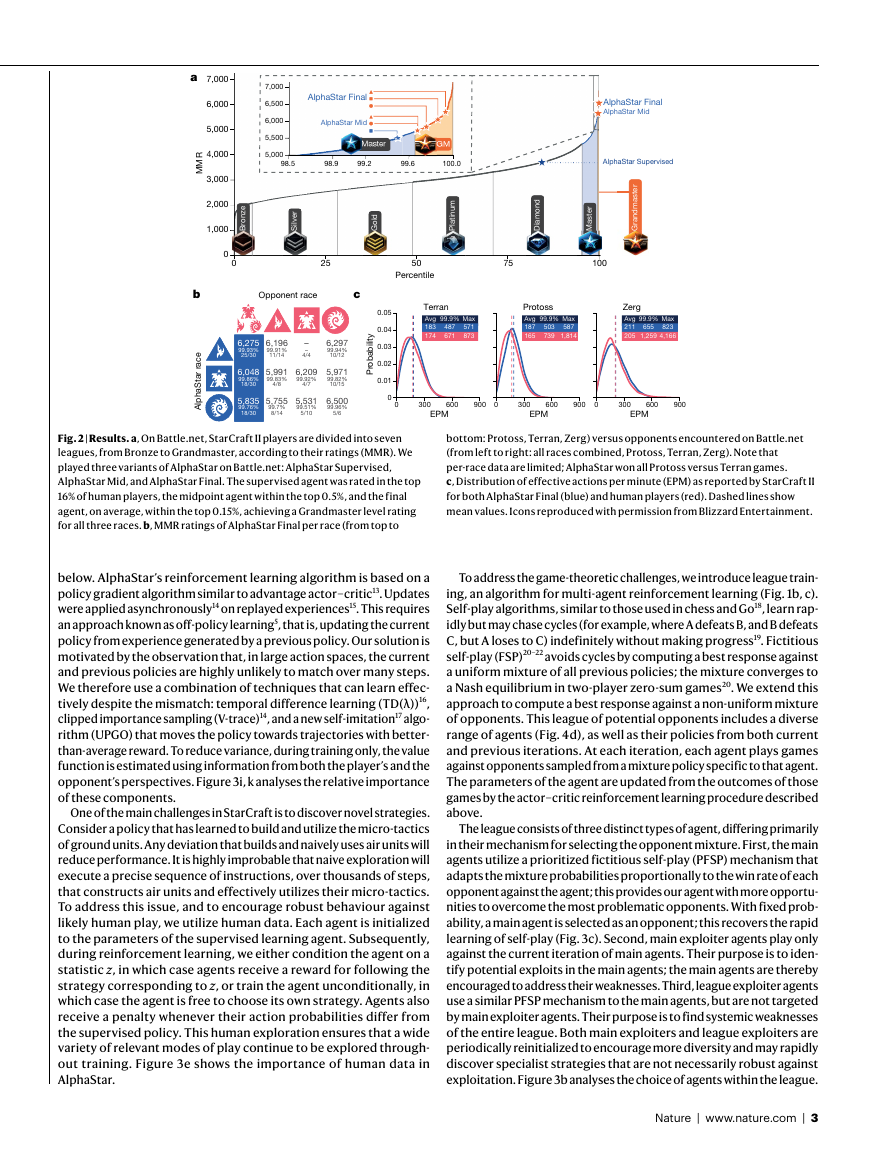
Fig. 2 | Results. a, On Battle.net, StarCraft II players are divided into seven
leagues, from Bronze to Grandmaster, according to their ratings (MMR). We
played three variants of AlphaStar on Battle.net: AlphaStar Supervised,
AlphaStar Mid, and AlphaStar Final. The supervised agent was rated in the top
16% of human players, the midpoint agent within the top 0.5%, and the final
agent, on average, within the top 0.15%, achieving a Grandmaster level rating
for all three races. b, MMR ratings of AlphaStar Final per race (from top to
bottom: Protoss, Terran, Zerg) versus opponents encountered on Battle.net
(from left to right: all races combined, Protoss, Terran, Zerg). Note that
per-race data are limited; AlphaStar won all Protoss versus Terran games.
c, Distribution of effective actions per minute (EPM) as reported by StarCraft II
for both AlphaStar Final (blue) and human players (red). Dashed lines show
mean values. Icons reproduced with permission from Blizzard Entertainment.
below. AlphaStar’s reinforcement learning algorithm is based on a
policy gradient algorithm similar to advantage actor–critic13. Updates
were applied asynchronously14 on replayed experiences15. This requires
an approach known as off-policy learning5, that is, updating the current
policy from experience generated by a previous policy. Our solution is
motivated by the observation that, in large action spaces, the current
and previous policies are highly unlikely to match over many steps.
We therefore use a combination of techniques that can learn effec-
tively despite the mismatch: temporal difference learning (TD(λ))16,
clipped importance sampling (V-trace)14, and a new self-imitation17 algo-
rithm (UPGO) that moves the policy towards trajectories with better-
than-average reward. To reduce variance, during training only, the value
function is estimated using information from both the player’s and the
opponent’s perspectives. Figure 3i, k analyses the relative importance
of these components.
One of the main challenges in StarCraft is to discover novel strategies.
Consider a policy that has learned to build and utilize the micro-tactics
of ground units. Any deviation that builds and naively uses air units will
reduce performance. It is highly improbable that naive exploration will
execute a precise sequence of instructions, over thousands of steps,
that constructs air units and effectively utilizes their micro-tactics.
To address this issue, and to encourage robust behaviour against
likely human play, we utilize human data. Each agent is initialized
to the parameters of the supervised learning agent. Subsequently,
during reinforcement learning, we either condition the agent on a
statistic z, in which case agents receive a reward for following the
strategy corresponding to z, or train the agent unconditionally, in
which case the agent is free to choose its own strategy. Agents also
receive a penalty whenever their action probabilities differ from
the supervised policy. This human exploration ensures that a wide
variety of relevant modes of play continue to be explored through-
out training. Figure 3e shows the importance of human data in
AlphaStar.
To address the game-theoretic challenges, we introduce league train-
ing, an algorithm for multi-agent reinforcement learning (Fig. 1b, c).
Self-play algorithms, similar to those used in chess and Go18, learn rap-
idly but may chase cycles (for example, where A defeats B, and B defeats
C, but A loses to C) indefinitely without making progress19. Fictitious
self-play (FSP)20–22 avoids cycles by computing a best response against
a uniform mixture of all previous policies; the mixture converges to
a Nash equilibrium in two-player zero-sum games20. We extend this
approach to compute a best response against a non-uniform mixture
of opponents. This league of potential opponents includes a diverse
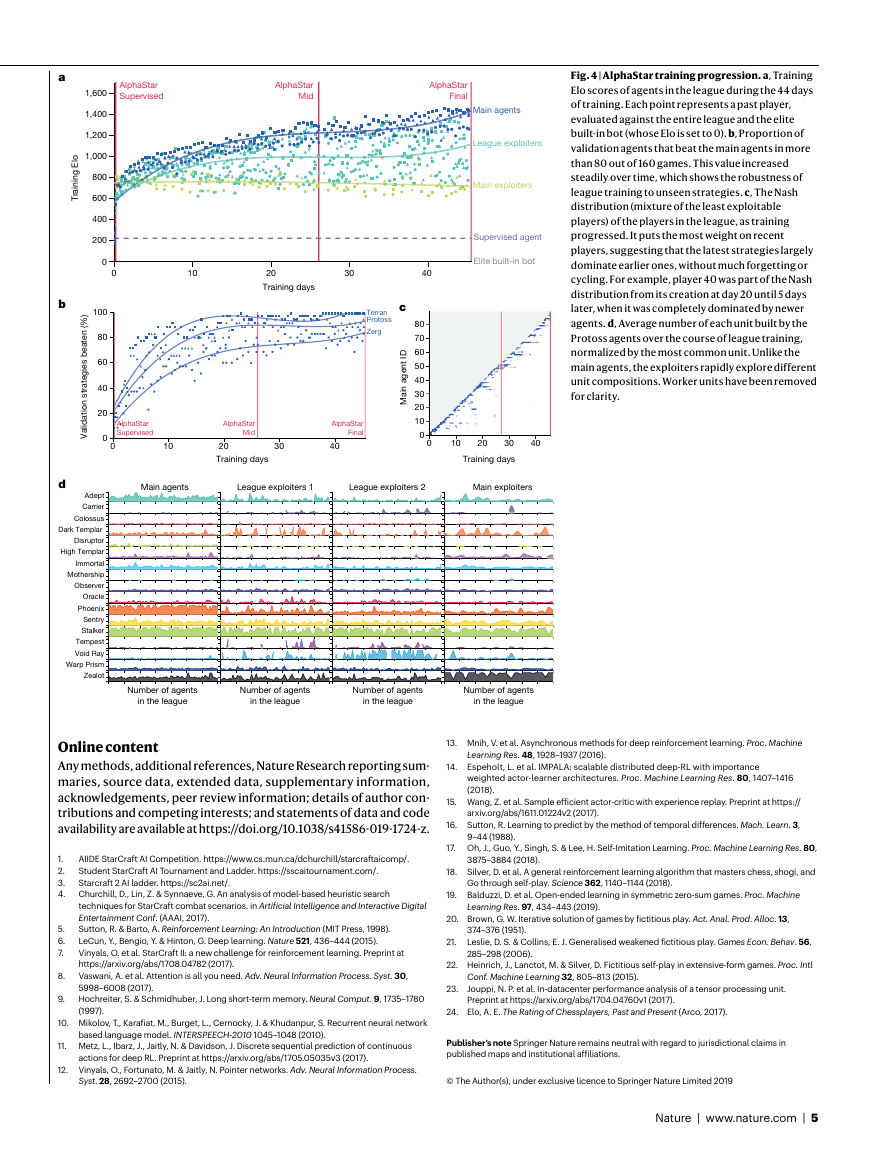
range of agents (Fig. 4d), as well as their policies from both current
and previous iterations. At each iteration, each agent plays games
against opponents sampled from a mixture policy specific to that agent.
The parameters of the agent are updated from the outcomes of those
games by the actor–critic reinforcement learning procedure described
above.
The league consists of three distinct types of agent, differing primarily
in their mechanism for selecting the opponent mixture. First, the main
agents utilize a prioritized fictitious self-play (PFSP) mechanism that
adapts the mixture probabilities proportionally to the win rate of each
opponent against the agent; this provides our agent with more opportu-
nities to overcome the most problematic opponents. With fixed prob-
ability, a main agent is selected as an opponent; this recovers the rapid
learning of self-play (Fig. 3c). Second, main exploiter agents play only
against the current iteration of main agents. Their purpose is to iden-
tify potential exploits in the main agents; the main agents are thereby
encouraged to address their weaknesses. Third, league exploiter agents
use a similar PFSP mechanism to the main agents, but are not targeted
by main exploiter agents. Their purpose is to find systemic weaknesses
of the entire league. Both main exploiters and league exploiters are
periodically reinitialized to encourage more diversity and may rapidly
discover specialist strategies that are not necessarily robust against
exploitation. Figure 3b analyses the choice of agents within the league.
Nature | www.nature.com | 3
a League composition
+ League exploiters
+ Main exploiters
Main agents
1,824
1,693
1,540
b
League composition
+ League exploiters
+ Main exploiters
Main agents
6%
62%
35%
0
600
c Multi-agent learning
1,200
Test Elo
1,800
2,400
pFSP + SP
SP
pFSP
FSP
0
600
e Human data usage
+ Statistics z
+ Supervised KL
Human init
Supervised
No human data
149
0
600
g APM limits
1,540
1,519
1,273
1,143
1,200
Test Elo
1,800
2,400
1,540
1,400
1,020
936
1,200
Test Elo
1,800
2,400
1,392
1,411
1,540
1,536
1,419
1,145
1,200
Test Elo
1,800
2,400
No APM limit
200% APM limit
100% APM limit
50% APM limit
25% APM limit
10% APM limit
0% APM limit
0
0
600
j Bots baselines
Built-in elite bot
603
Built-in very easy bot
418
No-op
0
0
600
1,200
Test Elo
1,800
2,400
0
25
50
75
100
Relative population performance (%)
d
Multi-agent learning
pFSP + SP
SP
pFSP
FSP
0
f Architectures
+ Scatter connections
+ Transformer
+ Pointer network
+ Action delays
7%
Baseline
0%
46%
71%
70%
69%
25
75
Min win rate vs past (%)
50
100
87%
71%
36%
h Interface
Non-camera interface
Camera interface
i Off-policy learning
+ UPGO
+ TD()
V-Trace
k Value function
With opponent info
Without opponent info
0
0
0
0
25
50
Supervised win rate vs elite bot (%)
75
100
96%
87%
25
50
75
100
Supervised win rate vs elite bot (%)
82%
73%
49%
25
50
75
100
Avg. win rate (%)
82%
22%
25
50
75
100
Avg. win rate (%)
Fig. 3 | Ablations for key components of AlphaStar.
These experiments use a simplified setup: one map
(Kairos Junction), one race match-up (Protoss versus
Protoss), reinforcement learning and league
experiments limited to 1010 steps, only main agents,
and a 50%–50% mix of self-play and PFSP, unless
stated otherwise (see Methods). The first column
shows Elo ratings24 against ablation test agents (each
rating was estimated with 11,000 full games of
StarCraft II). a, b, Comparing different league
compositions using Elo of the main agents (a) and
relative population performance of the whole
leagues (b), which measures exploitability. c, d,
Comparing different multi-agent learning algorithms
using Elo (c) and a proxy for forgetting: the minimum
win rate against all past versions, averaged over time
(d). Naive self-play has a high Elo, but is more
forgetful. See Extended Data Fig. 5 for more in-depth
comparison. e, Ablation study of the different
mechanisms to use human data. Human init,
supervised learning initialization of parameters of
the neural network. g, APM limits relative to those
used in AlphaStar. Reducing APM substantially
reduces performance. Unexpectedly, increasing APM
also reduces performance, possibly because the
agent spends more effort on refining micro-tactics
than on learning diverse strategies. f, h, Comparison
of architectures using the win rate of supervised
agents (trained in Protoss versus all) against the built-
in elite bot. j, Elo scores of StarCraft II built-in bots.
Ratings are anchored by a bot that never acts. i, k,
Reinforcement learning ablations, measured by
training a best response against fixed opponents to
avoid multi-agent dynamics.
In StarCraft, each player chooses one of three races—Terran, Protoss
or Zerg—each with distinct mechanics. We trained the league using
three main agents (one for each StarCraft race), three main exploiter
agents (one for each race), and six league exploiter agents (two for
each race). Each agent was trained using 32 third-generation tensor
processing units (TPUs23) over 44 days. During league training almost
900 distinct players were created.
Empirical evaluation
We evaluated the three main Terran, Protoss and Zerg AlphaStar agents
using the unconditional policy on the official online matchmaking
system Battle.net. Each agent was assessed at three different snapshots
during training: after supervised training only (AlphaStar Supervised),
after 27 days of league training (AlphaStar Mid), and after 44 days of
league training (AlphaStar Final). AlphaStar Supervised and AlphaStar
Mid were evaluated starting from an unranked rating on Battle.net
for 30 and 60 games, respectively, for each race; AlphaStar Final was
evaluated from AlphaStar Mid’s rating for an additional 30 games for
each race. The Battle.net matchmaking procedure selected maps and
opponents. Matches were played under blind conditions: AlphaStar
was not provided with the opponent’s identity, and played under an
anonymous account. These conditions were selected to estimate
AlphaStar’s strength under approximately stationary conditions,
but do not directly measure its susceptibility to exploitation under
repeated play.
AlphaStar Final achieved ratings of 6,275 Match Making Rating
(MMR) for Protoss, 6,048 MMR for Terran and 5,835 MMR for Zerg,
placing it above 99.8% of ranked human players, and at Grandmas-
ter level for all three races (Fig. 2a, Extended Data Fig. 7 (analysis),
Supplementary Data, Replays (game replays)). AlphaStar Super-
vised reached an average rating of 3,699, which places it above 84%
of human players and shows the effectiveness of supervised
learning.
To further analyse AlphaStar we also ran several internal ablations
(Fig. 3) and evaluations (Fig. 4). For multi-agent dynamics, we ran a
round-robin tournament of all players throughout league training
and a second tournament of main agents against held-out validation
agents trained to follow specific human strategies. The main agent
performance improved steadily across all three races. The perfor-
mance of the main exploiters actually reduced over time and main
agents performed better against the held-out validation agents, both
of which suggest that the main agent grew increasingly robust. The
league Nash equilibrium over all players at each point in time assigns
small probabilities to players from previous iterations, suggesting
that the learning algorithm does not cycle or regress. Finally, the unit
composition changed throughout league training, which indicates a
diverse strategic progression.
Conclusion
AlphaStar is the first agent to achieve Grandmaster level in
StarCraft II, and the first to reach the highest league of human players
in a widespread professional esport without simplification of the
game. Like StarCraft, real-world domains such as personal assistants,
self-driving cars, or robotics require real-time decisions, over com-
binatorial or structured action spaces, given imperfectly observed
information. Furthermore, similar to StarCraft, many applications
have complex strategy spaces that contain cycles or hard explora-
tion landscapes, and agents may encounter unexpected strategies
or complex edge cases when deployed in the real world. The success
of AlphaStar in StarCraft II suggests that general-purpose machine
learning algorithms may have a substantial effect on complex
real-world problems.
4 | Nature | www.nature.com
Article
Fig. 4 | AlphaStar training progression. a, Training
Elo scores of agents in the league during the 44 days
of training. Each point represents a past player,
evaluated against the entire league and the elite
built-in bot (whose Elo is set to 0). b, Proportion of
validation agents that beat the main agents in more
than 80 out of 160 games. This value increased
steadily over time, which shows the robustness of
league training to unseen strategies. c, The Nash
distribution (mixture of the least exploitable
players) of the players in the league, as training
progressed. It puts the most weight on recent
players, suggesting that the latest strategies largely
dominate earlier ones, without much forgetting or
cycling. For example, player 40 was part of the Nash
distribution from its creation at day 20 until 5 days
later, when it was completely dominated by newer
agents. d, Average number of each unit built by the
Protoss agents over the course of league training,
normalized by the most common unit. Unlike the
main agents, the exploiters rapidly explore different
unit compositions. Worker units have been removed
for clarity.
a
b
l
o
E
g
n
n
a
r
T
i
i
AlphaStar
Supervised
AlphaStar
Mid
AlphaStar
Final
1,600
1,400
1,200
1,000
800
600
400
200
0
0
10
20
Training days
30
40
Main agents
League exploiters
Main exploiters
Supervised agent
Elite built-in bot
100
80
60
40
20
)
%
(
i
n
e
t
a
e
b
s
e
g
e
t
a
r
t
s
n
o
i
t
a
d
i
l
a
0V
0
AlphaStar
Supervised
10
AlphaStar
Mid
20
Training days
30
AlphaStar
Final
40
Terran
Protoss
Zerg
c
D
I
t
n
e
g
a
i
n
a
M
80
70
60
50
40
30
20
10
0
0
10
20
30
40
Training days
d
Adept
Carrier
Colossus
Dark Templar
Disruptor
High Templar
Immortal
Mothership
Observer
Oracle
Phoenix
Sentry
Stalker
Tempest
Void Ray
Warp Prism
Zealot
Main agents
League exploiters 1
League exploiters 2
Main exploiters
Number of agents
in the league
Number of agents
in the league
Number of agents
in the league
Number of agents
in the league
Online content
Any methods, additional references, Nature Research reporting sum-
maries, source data, extended data, supplementary information,
acknowledgements, peer review information; details of author con-
tributions and competing interests; and statements of data and code
availability are available at https://doi.org/10.1038/s41586-019-1724-z.
13. Mnih, V. et al. Asynchronous methods for deep reinforcement learning. Proc. Machine
Learning Res. 48, 1928–1937 (2016).
14. Espeholt, L. et al. IMPALA: scalable distributed deep-RL with importance
weighted actor-learner architectures. Proc. Machine Learning Res. 80, 1407–1416
(2018).
15. Wang, Z. et al. Sample efficient actor-critic with experience replay. Preprint at https://
arxiv.org/abs/1611.01224v2 (2017).
16. Sutton, R. Learning to predict by the method of temporal differences. Mach. Learn. 3,
AIIDE StarCraft AI Competition. https://www.cs.mun.ca/dchurchill/starcraftaicomp/.
Student StarCraft AI Tournament and Ladder. https://sscaitournament.com/.
1.
2.
3. Starcraft 2 AI ladder. https://sc2ai.net/.
4. Churchill, D., Lin, Z. & Synnaeve, G. An analysis of model-based heuristic search
techniques for StarCraft combat scenarios. in Artificial Intelligence and Interactive Digital
Entertainment Conf. (AAAI, 2017).
Sutton, R. & Barto, A. Reinforcement Learning: An Introduction (MIT Press, 1998).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Vinyals, O. et al. StarCraft II: a new challenge for reinforcement learning. Preprint at
https://arxiv.org/abs/1708.04782 (2017).
5.
6.
7.
8. Vaswani, A. et al. Attention is all you need. Adv. Neural Information Process. Syst. 30,
9. Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780
5998–6008 (2017).
(1997).
10. Mikolov, T., Karafiat, M., Burget, L., Cernocky, J. & Khudanpur, S. Recurrent neural network
based language model. INTERSPEECH-2010 1045–1048 (2010).
11. Metz, L., Ibarz, J., Jaitly, N. & Davidson, J. Discrete sequential prediction of continuous
actions for deep RL. Preprint at https://arxiv.org/abs/1705.05035v3 (2017).
12. Vinyals, O., Fortunato, M. & Jaitly, N. Pointer networks. Adv. Neural Information Process.
Syst. 28, 2692–2700 (2015).
9–44 (1988).
3875–3884 (2018).
17. Oh, J., Guo, Y., Singh, S. & Lee, H. Self-Imitation Learning. Proc. Machine Learning Res. 80,
18. Silver, D. et al. A general reinforcement learning algorithm that masters chess, shogi, and
Go through self-play. Science 362, 1140–1144 (2018).
19. Balduzzi, D. et al. Open-ended learning in symmetric zero-sum games. Proc. Machine
Learning Res. 97, 434–443 (2019).
20. Brown, G. W. Iterative solution of games by fictitious play. Act. Anal. Prod. Alloc. 13,
374–376 (1951).
285–298 (2006).
21. Leslie, D. S. & Collins, E. J. Generalised weakened fictitious play. Games Econ. Behav. 56,
22. Heinrich, J., Lanctot, M. & Silver, D. Fictitious self-play in extensive-form games. Proc. Intl
Conf. Machine Learning 32, 805–813 (2015).
23. Jouppi, N. P. et al. In-datacenter performance analysis of a tensor processing unit.
Preprint at https://arxiv.org/abs/1704.04760v1 (2017).
24. Elo, A. E. The Rating of Chessplayers, Past and Present (Arco, 2017).
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in
published maps and institutional affiliations.
© The Author(s), under exclusive licence to Springer Nature Limited 2019
Nature | www.nature.com | 5
Methods
Game and interface
Game environment. StarCraft is a real-time strategy game that takes
place in a science fiction universe. The franchise, from Blizzard Enter-
tainment, comprises StarCraft: Brood War and StarCraft II. In this paper,
we used StarCraft II. Since StarCraft was released in 1998, there has
been a strong competitive community with tens of millions of dollars
of prize money. The most common competitive setting of StarCraft
II is 1v1, where each player chooses one of the three available races—
Terran, Protoss, and Zerg—which all have distinct units and buildings,
exhibit different mechanics, and necessitate different strategies when
playing for and against. There is also a Random race, where the game
selects the player’s race at random. Players begin with a small base and
a few worker units, which gather resources to build additional units
and buildings, scout the opponent, and research new technologies. A
player is defeated if they lose all buildings.
There is no universally accepted notion of fairness in real-time
human–computer matches, so our match conditions, interface, camera
view, action rate limits, and delays were developed in consultation with
professional StarCraft II players and Blizzard employees. AlphaStar’s
play under these conditions was professional-player approved (see the
Professional Player Statement, below). At each agent step, the policy
receives an observation ot and issues an action at (Extended Data
Tables 1, 2) through the game interface. There can be several game
time-steps (each 45 ms) per agent step.
Camera view. Humans play StarCraft through a screen that displays
only part of the map along with a high-level view of the entire map
(to avoid information overload, for example). The agent interacts with
the game through a similar camera-like interface, which naturally im-
poses an economy of attention, so that the agent chooses which area
it fully sees and interacts with. The agent can move the camera as an
action.
Opponent units outside the camera have certain information hidden,
and the agent can only target within the camera for certain actions (for
example, building structures). AlphaStar can target locations more
accurately than humans outside the camera, although less accurately
within it because target locations (selected on a 256 × 256 grid) are
treated the same inside and outside the camera. Agents can also select
sets of units anywhere, which humans can do less flexibly using control
groups. In practice, the agent does not seem to exploit these extra
capabilities (see the Professional Player Statement, below), because of
the human prior. Ablation data in Fig. 3h shows that using this camera
view reduces performance.
APM limits. Humans are physically limited in the number of actions
per minute (APM) they can execute. Our agent has a monitoring layer
that enforces APM limitations. This introduces an action economy that
requires actions to be prioritized. Agents are limited to executing at
most 22 non-duplicate actions per 5-s window. Converting between
actions and the APM measured by the game is non-trivial, and agent ac-
tions are hard to compare with human actions (computers can precisely
execute different actions from step to step). See Fig. 2c and Extended
Data Fig. 1 for APM details.
Delays. Humans are limited in how quickly they react to new informa-
tion; AlphaStar has two sources of delays. First, in real-time evaluation
(not training), AlphaStar has a delay of about 110 ms between when a
frame is observed and when an action is executed, owing to latency,
observation processing, and inference. Second, because agents
decide ahead of time when to observe next (on average 370 ms,
but possibly multiple seconds), they may react late to unexpected
situations. The distribution of these delays is shown in Extended
Data Fig. 2.
Related work
Games have been a focus of artificial intelligence research for decades
as a stepping stone towards more general applications. Classic board
games such as chess25 and Go26 have been mastered using general-
purpose reinforcement learning and planning algorithms18. Reinforce-
ment learning methods have achieved substantial successes in video
games such as those on the Atari platform27, Super Mario Bros28, Quake
III Arena Capture the Flag29, and Dota 230.
Real-time strategy (RTS) games are recognized for their game-
theoretic and domain complexities31. Many sub-problems of RTS games,
for example, micromanagement, base economy, or build order opti-
mization, have been studied in depth7,32–35, often in small-scale envi-
ronments36,37. For the combined challenge, the StarCraft domain has
emerged by consensus as a research focus1,7. StarCraft: Brood War has
an active competitive AI research community38, and most bots com-
bine rule-based heuristics with other AI techniques such as search4,39,
data-driven build-order selection40, and simulation41. Reinforcement
learning has also been studied to control units in the game7,34,42–44,
and imitation learning has been proposed to learn unit and building
compositions45. Most recently, deep learning has been used to predict
future game states46. StarCraft II similarly has an active bot community3
since the release of a public application programming interface (API)7.
No StarCraft bots have defeated professional players, or even high-level
casual players47, and the most successful bots have used superhuman
capabilities, such as executing tens of thousands of APM or viewing
the entire map at once. These capabilities make comparisons against
humans hard, and invalidate certain strategies. Some of the most recent
approaches use reinforcement learning to play the full game, with
hand-crafted, high-level actions48, or rule-based systems with machine
learning incrementally replacing components43. By contrast, AlphaStar
uses a model-free, end-to-end learning approach to playing StarCraft
II that sidesteps the difficulties of search-based methods that result
from imperfect models, and is applicable to any domain that shares
some of the challenges present in StarCraft.
Dota 2 is a modern competitive team game that shares some com-
plexities of RTS games such as StarCraft (including imperfect informa-
tion and large time horizons). Recently, OpenAI Five defeated a team
of professional Dota 2 players and 99.4% of online players30. The hero
units of OpenAI Five are controlled by a team of agents, trained together
with a scaled up version of PPO49, based on handcrafted rewards. How-
ever, unlike AlphaStar, some game rules were simplified, players were
restricted to a subset of heroes, agents used hard-coded sub-systems
for certain aspects of the game, and agents did not limit their percep-
tion to a camera view.
AlphaStar relies on imitation learning combined with reinforcement
learning, which has been used several times in the past. Similarly to the
training pipeline of AlphaStar, the original AlphaGo initialized a policy
network by supervised learning from human games, which was then
used as a prior in Monte-Carlo tree search26. Similar to our statistic z,
other work attempted to train reward functions from human prefer-
ences and use them to guide reinforcement learning50,51 or learned
goals from human intervention52.
Related to the league, recent progress in multi-agent research has led
to agents performing at human level in the Capture the Flag team mode
of Quake III Arena29. These results were obtained using population-
based training of several agents competing with each other, which
used pseudo-reward evolution to deal with the hard credit assignment
problem. Similarly, the Policy Space Response Oracle framework53 is
related to league training, although league training specifies unique
targets for approximate best responses (that is, PFSP and exploiters).
Architecture
The policy of AlphaStar is a function πθ(at | st,z) that maps all previous
observations and actions st = o1:t, a1:t − 1 (defined in Extended Data Tables 1, 2)
Article
and z (representing strategy statistics) to a probability distribution
over actions at for the current step. πθ is implemented as a deep neural
network with the following structure.
The observations ot are encoded into vector representations,
combined, and processed by a deep LSTM9, which maintains
memory between steps. The action arguments at are sampled auto-
regressively10, conditioned on the outputs of the LSTM and the observa-
tion encoders. There is a value function for each of the possible rewards
(see Reinforcement learning).
Architecture components were chosen and tuned with respect to
their performance in supervised learning, and include many recent
advances in deep learning architectures7,8,12,54,55. A high-level overview
of the agent architecture is given in Extended Data Fig. 3, with more
detailed descriptions in Supplementary Data, Detailed Architecture.
AlphaStar has 139 million weights, but only 55 million weights are
required during inference. Ablation Fig. 3f compares the impact of
scatter connections, transformer, and pointer network.
Supervised learning
Each agent is initially trained through supervised learning on replays
to imitate human actions. Supervised learning is used both to initialize
the agent and to maintain diverse exploration56. Because of this, the
primary goal is to produce a diverse policy that captures StarCraft’s
complexities.
We use a dataset of 971,000 replays played on StarCraft II versions
4.8.2 to 4.8.6 by players with MMR scores (Blizzard’s metric, similar to
Elo) greater than 3,500, that is, from the top 22% of players. Instruc-
tions for downloading replays can be found at https://github.com/
Blizzard/s2client-proto. The observations and actions are returned
by the game’s raw interface (Extended Data Tables 1, 2). We train one
policy for each race, with the same architecture as the one used during
reinforcement learning.
From each replay, we extract a statistic z that encodes each player’s
build order, defined as the first 20 constructed buildings and units,
and cumulative statistics, defined as the units, buildings, effects, and
upgrades that were present during a game. We condition the policy
on z in both supervised and reinforcement learning, and in supervised
learning we set z to zero 10% of the time.
To train the policy, at each step we input the current observations
and output a probability distribution over each action argument
(Extended Data Table 2). For these arguments, we compute the KL
divergence between human actions and the policy’s outputs, and apply
updates using the Adam optimizer57. We also apply L2 regularization58.
The pseudocode of the supervised training algorithm can be found
in Supplementary Data, Pseudocode.
We further fine-tune the policy using only winning replays with MMR
above 6,200 (16,000 games). Fine-tuning improved the win rate against
the built-in elite bot from 87% to 96% in Protoss versus Protoss games.
The fine-tuned supervised agents were rated at 3,947 MMR for Terran,
3,607 MMR for Protoss and 3,544 MMR for Zerg. They are capable of
building all units in the game, and are qualitatively diverse from game
to game (Extended Data Fig. 4).
Reinforcement learning
We apply reinforcement learning to improve the performance of
AlphaStar based on agent-versus-agent games. We use the match out-
come (−1 on a loss, 0 on a draw and +1 on a win) as the terminal reward
rT, without a discount to accurately reflect the true goal of winning
games. Following the actor–critic paradigm14, a value function Vθ(st, z)
is trained to predict rt, and used to update the policy πθ(at | st, z).
StarCraft poses several challenges when viewed as a reinforcement
learning problem: exploration is difficult, owing to domain complexity
and reward sparsity; policies need to be capable of executing diverse
strategies throughout training; and off-policy learning is difficult,
owing to large time horizons and the complex action space.
Exploration and diversity. We use human data to aid in exploration
and to preserve strategic diversity throughout training. First, we
initialize the policy parameters to the supervised policy and continu-
ally minimize the KL divergence between the supervised and current
policy59,60. Second, we train the main agents with pseudo-rewards to
follow a strategy statistic z, which we randomly sample from human
data. These pseudo-rewards measure the edit distance between sam-
pled and executed build orders, and the Hamming distance between
sampled and executed cumulative statistics (see Supplementary Data,
Detailed Architecture). Each type of pseudo-reward is active (that is,
non-zero) with probability 25%, and separate value functions and losses
are computed for each pseudo-reward. We found our use of human
data to be critical in achieving good performance with reinforcement
learning (Fig. 3e).
Value and policy updates. New trajectories are generated by actors.
Asynchronously, model parameters are updated by learners, using
a replay buffer that stores trajectories. Because of this, AlphaStar is
subject to off-policy data, which potentially requires off-policy cor-
rections. We found that existing off-policy correction methods14,61
can be inefficient in large, structured action spaces such as that used
for StarCraft, because distinct actions can result in similar (or even
identical) behaviour. We addressed this by using a hybrid approach
that combines off-policy corrections for the policy (which avoids
instability), with an uncorrected update of the value function (which
introduces bias but reduces variance). Specifically, the policy is
updated using V-trace and the value estimates are updated using
TD(λ)5 (ablation in Fig. 3i). When applying V-trace to the policy in
large action spaces, the off-policy corrections truncate the trace
early; to mitigate this problem, we assume independence between
the action type, delay, and all other arguments, and so update the
components of the policy separately. To decrease the variance of
the value estimates, we also use the opponent’s observations as
input to the value functions (ablation in Fig. 3k). Note that these
are used only during training, as value functions are unnecessary
during evaluation.
In addition to the V-trace policy update, we introduce an upgoing
policy update (UPGO), which updates the policy parameters in the
direction of
(
ρ G V s z
t
− (
θ
t
U
t
π a s z
, ))∇ log (
, )
θ
θ
|
t
t
where
U
G
t
=
U
r G
+
t
t
+1
r V s
+ (
t
θ
t
if
Q s
(
a
t
z
, ) otherwise
,
+1
t
+1
z
V s
, ) ≥ (
θ
+1
t
z
, )
+1
|
|
θ
θ
′
, 1
)
(
s z
, )
t
s z
, )
t
π a
(
t
π a
(
t
is an upgoing return, Q(st,at,z) is an action-value estimate,
is a clipped importance ratio, and πθ′ is the
ρ = min
t
policy that generated the trajectory in the actor. Similar to self-
imitation learning17, the idea is to update the policy from partial tra-
jectories with better-than-expected returns by bootstrapping when
the behaviour policy takes a worse-than-average action (ablation in
Fig. 3i). Owing to the difficulty of approximating Q(st, at, z) over the
large action space of StarCraft, we estimate action-values with a
one-step target, Q(st, at, z) = rt + Vθ(st + 1, z).
The overall loss is a weighted sum of the policy and value function
losses described above, corresponding to the win-loss reward rt as well
as pseudo-rewards based on human data, the KL divergence loss with
respect to the supervised policy, and the standard entropy regulariza-
tion loss13. We optimize the overall loss using Adam57. The pseudocode
of the reinforcement learning algorithm can be found in Supplementary
Data, Pseudocode.
Multi-agent learning
League training is a multi-agent reinforcement learning algorithm that
is designed both to address the cycles commonly encountered during
self-play training and to integrate a diverse range of strategies. During
training, we populate the league by regularly saving the parameters
from our agents (that are being trained by the RL algorithm) as new
players (which have fixed, frozen parameters). We also continuously
re-evaluate the internal payoff estimation, giving agents up-to-date
information about their performance against all players in the league
(see evaluators in Extended Data Fig. 6).
Prioritized fictitious self-play. Our self-play algorithm plays games
between the latest agents for all three races. This approach may chase
cycles in strategy space and does not work well in isolation (Fig. 3d).
FSP20–22 avoids cycles by playing against all previous players in the
league. However, many games are wasted against players that are de-
feated in almost 100% of games. Consequently, we introduce PFSP.
Instead of uniformly sampling opponents in the league, we use a match-
making mechanism to provide a good learning signal. Given a learning
agent A, we sample the frozen opponent B from a candidate set C with
probability
f
∑
C∈
C
ℙ
A
( [ beats ])
ℙ
C
f
( [ beats ])
A
B
Where f: [0, 1] → [0, ∞) is some weighting function.
Choosing fhard(x) = (1 − x)p makes PFSP focus on the hardest players,
where p ∈ ℝ+ controls how entropic the resulting distribution is. As
fhard(1) = 0, no games are played against opponents that the agent already
beats. By focusing on the hardest players, the agent must beat everyone
in the league rather than maximizing average performance, which is
even more important in highly non-transitive games such as StarCraft
(Extended Data Fig. 8), where the pursuit of the mean win rate might
lead to policies that are easy to exploit. This scheme is used as the
default weighting of PFSP. Consequently, on the theoretical side, one
can view fhard as a form of smooth approximation of max–min optimiza-
tion, as opposed to max–avg, which is imposed by FSP. In particular,
this helps with integrating information from exploits, as these are
strong but rare counter strategies, and a uniform mixture would be
able to just ignore them (Extended Data Fig. 5).
Only playing against the hardest opponents can waste games against
much stronger opponents, so PFSP also uses an alternative curriculum,
fvar(x) = x(1 − x), where the agent preferentially plays against opponents
around its own level. We use this curriculum for main exploiters and
struggling main agents.
Populating the league. During training we used three agent types
that differ only in the distribution of opponents they train against,
when they are snapshotted to create a new player, and the probability
of resetting to the supervised parameters.
Main agents are trained with a proportion of 35% SP, 50% PFSP
against all past players in the league, and an additional 15% of PFSP
matches against forgotten main players the agent can no longer beat
and past main exploiters. If there are no forgotten players or strong
exploiters, the 15% is used for self-play instead. Every 2 × 109 steps, a
copy of the agent is added as a new player to the league. Main agents
never reset.
League exploiters are trained using PFSP and their frozen copies are
added to the league when they defeat all players in the league in more
than 70% of games, or after a timeout of 2 × 109 steps. At this point there
is a 25% probability that the agent is reset to the supervised parameters.
The intuition is that league exploiters identify global blind spots in the
league (strategies that no player in the league can beat, but that are not
necessarily robust themselves).
Main exploiters play against main agents. Half of the time, and if the
current probability of winning is lower than 20%, exploiters use PFSP
with fvar weighting over players created by the main agents. This forms
a curriculum that facilitates learning. Otherwise there is enough learn-
ing signal and it plays against the current main agents. These agents
are added to the league whenever all three main agents are defeated
in more than 70% of games, or after a timeout of 4 × 109 steps. They
are then reset to the supervised parameters. Main exploiters identify
weaknesses of main agents, and consequently make them more robust.
For more details refer to the Supplementary Data, Pseudocode.
Infrastructure
In order to train the league, we run a large number of StarCraft II
matches in parallel and update the parameters of the agents on the
basis of data from those games. To manage this, we developed a highly
scalable training setup with different types of distributed workers.
For every training agent in the league, we run 16,000 concurrent
StarCraft II matches and 16 actor tasks (each using a TPU v3 device
with eight TPU cores23) to perform inference. The game instances pro-
gress asynchronously on preemptible CPUs (roughly equivalent to 150
processors with 28 physical cores each), but requests for agent steps
are batched together dynamically to make efficient use of the TPU.
Using TPUs for batched inference provides large efficiency gains over
previous work14,29.
Actors send sequences of observations, actions, and rewards over
the network to a central 128-core TPU learner worker, which updates
the parameters of the training agent. The received data are buffered in
memory and replayed twice. The learner worker performs large-batch
synchronous updates. Each TPU core processes a mini-batch of four
sequences, for a total batch size of 512. The learner processes about
50,000 agent steps per second. The actors update their copy of the
parameters from the learner every 10 s.
We instantiate 12 separate copies of this actor–learner setup: one
main agent, one main exploiter and two league exploiter agents for
each StarCraft race. One central coordinator maintains an estimate of
the payoff matrix, samples new matches on request, and resets main
and league exploiters. Additional evaluator workers (running on the
CPU) are used to supplement the payoff estimates. See Extended Data
Fig. 6 for an overview of the training setup.
Evaluation
AlphaStar Battle.net evaluation. AlphaStar agents were evaluated
against humans on Battle.net, Blizzard’s online matchmaking system
based on MMR ratings, on StarCraft II balance patch 4.9.3. AlphaStar
Final was rated at Grandmaster level, above 99.8% of human players
who were active enough in the past months to be placed into a league
on the European server (about 90,000 players).
AlphaStar played only opponents who opted to participate in the
experiment (the majority of players opted in)62, used an anonymous
account name, and played on four maps: Cyber Forest, Kairos Junc-
tion, King’s Cove, and New Repugnancy. Blizzard updated the map
pool a few weeks before testing. Instead of retraining AlphaStar, we
simply played on the four common maps that were kept in the pool of
seven available maps. Humans also must select at least four maps and
frequently play under anonymous account names. Each agent ran on
a single high-end consumer GPU. We evaluated at three points during
training: supervised, midpoint, and final.
For the supervised and midpoint evaluations, each agent began with
a fresh, unranked account. Their MMR was updated on Battle.net as
for humans. The supervised and midpoint evaluations played 30 and
60 games, respectively. The midpoint evaluation was halted while
still increasing because the anonymity constraint was compromised
after 50 games.
For the final Battle.net evaluation, we used several accounts to par-
allelize the games and help to avoid identification. The MMRs of our
Article
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
