表面织构对活塞环-缸套接触压力分布影响的理论分析.pdf-资料库

5 10 15 20 25 30 35 40 中国科技论文在线 http://www.paper.edu.cn 表面织构对活塞环-缸套接触压力分布影响的理论分析吴一贤1，杨露露1，吕品1，翟华1，王虎2** （1. 合肥工业大学工业与装备技术研究院，合肥，230009； 2. 合肥工业大学机械工程学院，合肥，230009）摘要：本文基于一维平均雷诺方程,对具有表面织构的活塞环-缸套摩擦副系统，建立了活塞环-油膜-缸套系统的一维接触润滑模型，对具有矩形、三角形和椭圆形三种表面织构的缸套，分别得到了活塞环-缸套接触压力的简化解析解，并进行了活塞环-缸套间接触压力的分析和比较。计算结果表明，缸套上三种纹理结构对接触压力的分布和变化具有不同的影响。缸套上是矩形表面织构时,织构区域的压力沿直线变小；缸套上是三角形和椭圆形表面织构时，织构区域的压力沿曲线变小，并且椭圆表面织构区域的接触压力变化要比三角形表面织构区域的接触压力变化平缓。因此，采用椭圆形表面织构可以较好的改善活塞环-缸套的接触压力分布情况，提高活塞环的工作性能和使用寿命。关键词：活塞环；缸套；表面织构；接触压力；流体润滑模型中图分类号：TH122 Theoretical analysis on the influence of piston ring-cylinder contact pressure distribution for surface texture Wu Yi-xian1, Yang Lulu1, Lu Pin1, Zhai Hua1, Wang Hu2 (1. Institute of Industry and Equipment Technology,Hefei University of Technology, Hefei 230009; 2. School of Mechanical Engineer ing, Hefei University of Technology, Hefei 230009) Abstrac t:In this paper, the contact pressure distribution between a textured cylinder liner and a piston ring is studied based on one-dimensional average Reynolds equations. The simp lified analytical relations of the contact pressure distributions for the piston ring/textured cylinder systems with rectangular, triangular and elliptica l cylinder-surface te xtures, respectively, are derived. The numerical results show that the three types of the cylinder surface texture structures have different effects on the contact pressure distributions. The variations of the contact pressures in the textured regions with the rectangular and the triangular te xtures are seen sharper than those with elliptical te xtu res, indicating that a re latively stable contact pressure distribution could be achieved for the cylinder with elliptical textures. Ke ywor ds: p iston ring; cylinder liner; surface te xture; contact p ressure; fluid lubricat ion model 0 引言内燃机广泛的应用于工业生产，交通运输行业中。活塞环-缸套摩擦副是内燃机中重要的摩擦副之一，其接触摩擦运动情况的好坏直接影响着内燃机的工作状况。活塞环-缸套间的压力过大会导致摩擦损耗增大，影响活塞环的使用寿命，使内燃机效率减小，还会出现拉缸现象；活塞环-缸套间的压力过小则会导致气密性不足，直接影响内燃机的动力输出。因此，改善活塞环-缸套间的接触摩擦性质一直是该领域关注的研究问题。近年来,通过表面织构技术来改善提高摩擦接触的润滑性能受到了广泛重视[1,2]。根据流作者简介：吴一贤（1991-），男，硕士研究生，主要研究方向：汽车活塞环受力理论分析通信联系人：吕品(1958-),男，博导，主要研究方向：理论力学建模与分析. E-mail: lupin@hfut.edu.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 45 体润滑理论，对考虑了表面织构摩擦副的接触摩擦数值分析也有很多报道 [3,4]。最近， Biboulet 等[5-7]根据活塞环-缸套接触的一维近似模型，得到了缸套具有三角纹理结构的摩擦副接触摩擦分析的解析表达式，简化了数值分析方法的计算量。本文在 Biboulet 等[5]的工作的基础上，对具有光滑、矩形、三角形和椭圆形等表面织构的缸套（如图 1 所示），分别得到了活塞环-缸套接触压力的简化解析解进行接触压力的分析，比较了这几种不同情况下活塞环-缸套间的压强分布和摩擦等性质，为内燃机摩擦副 50 的织构优化设计提供参数和依据。图 1 几种不同的缸套织构形式 A.矩形 B.三角形 C.椭圆形 D.平面 Fig. 1 Several texture forms on cylinder: A. rectangular, B. triangle, C. elliptic, D. plane 1 活塞环-缸套一维模型的基本方程和解析解 55 1.1 基本方程图 2 活塞环-油膜--缸套系统的一维的润滑接触模型 Fig. 2 Contact model of 1D piston ring-cylinder liner 60 图 2 为活塞环-油膜--缸套系统的一维的润滑接触模型示意图。活塞环-缸套间的油膜厚度可根据活塞环-缸套接触的几何模型来表示：（1）式中，h0 为最小油膜厚度，R 为活塞环的曲率半径。由于油膜厚度远小于活塞环的曲率半径，为后面推导方便，可将（1）式简化，近似表示为： 65 （2） - 2 - 220xRRhhRxhh220

中国科技论文在线 http://www.paper.edu.cn 定义无量纲变量 H=h/h0 和，式（2）写成无量纲的形式为[5]：（3）进一步定义无量纲变量（4） 70 式（2）可以表示成更简洁的形式为：（5）在（1）-（5）中，为后边讨论方便，活塞环-缸套间的油膜厚度变化分别用有量纲和无量纲的形式表示。本文中，除活塞环的曲率半径 R，大写字母变量均表示无量纲参量。图 2 所示的活塞环-油膜-缸套系统的润滑模型可用一维平均雷诺方程来描述：（6）式中为时间参数，为油膜压力，为油膜厚度, 为润滑油的粘度，假设为常数，为活塞环和缸套间的平均往复速度。假设最小油膜厚度为常数，考虑表面织构的活塞环-缸套间油膜厚度可以表示为[5]：（7）其中 hs 表示式（2）所定义的光滑活塞环-缸套间的油膜厚度，hg 则是表面织构纹理的结构尺寸在平均往复速度下引起的活塞环-缸套间油膜厚度变化。将（7）带入（6）可得到稳定状态的平均雷诺方程形式：（8） 75 80 由于方程中不显含时间参数，使求解简化，便于得到解析形式解。根据前面定义的无量纲参量，稳定状态的平均雷诺方程（8）可进一步表示为无量纲的形式为[5]： 85 （9） 1.2 光滑接触的解析解对于活塞环-缸套光滑接触的油膜压力可通过求解平均雷诺方程（9）求解得到一般解（10） 90 式中参数 Y 和 H 由（4）和（5）式给出，Z=Y/H，表示润滑油在活塞环-缸套接触出口位置处的油膜厚度。由（10）可知，出口处的油膜压力为，因此，活塞环-缸套间的油膜压力变化与出口处压力的差值为：（11）当运用式（10）和（11）计算活塞环-缸套接触时的压强分布时，可作为输入参数，以此 - 3 - 0/RhxX212XHY2XY21YHthxhxphxm0312tph0m0h)2()(,txhxhtxhmgsxhhxphxgsm0312XHHXPHXgs3HHZZYHPbbd4arctan83212bHbYHddYP)()(bddYPYPPbH

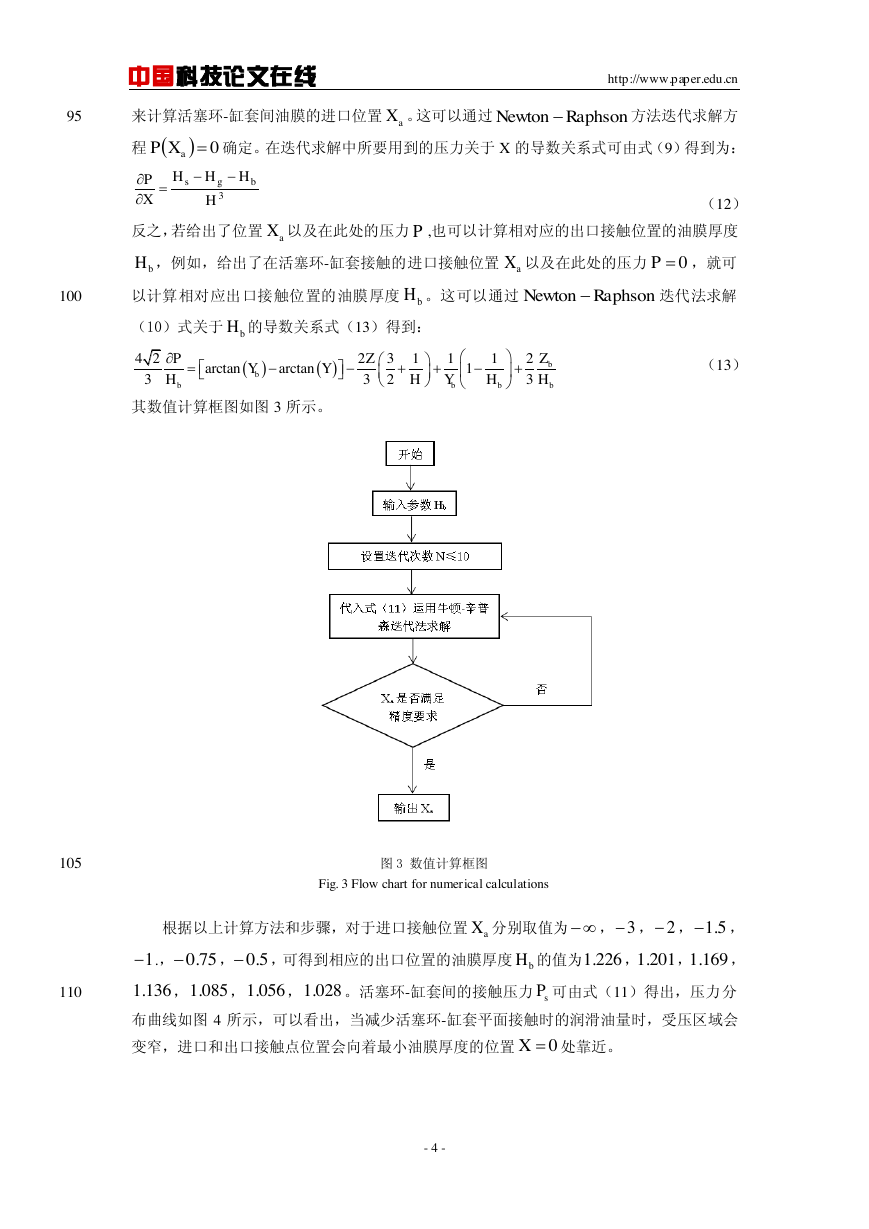
中国科技论文在线 http://www.paper.edu.cn 95 来计算活塞环-缸套间油膜的进口位置。这可以通过方法迭代求解方程确定。在迭代求解中所要用到的压力关于 X 的导数关系式可由式（9）得到为：（12）反之，若给出了位置以及在此处的压力 ,也可以计算相对应的出口接触位置的油膜厚度，例如，给出了在活塞环-缸套接触的进口接触位置以及在此处的压力，就可 100 以计算相对应出口接触位置的油膜厚度。这可以通过迭代法求解（10）式关于的导数关系式（13）得到：其数值计算框图如图 3 所示。（13） 105 图 3 数值计算框图 Fig. 3 Flow chart for numerical calculations 根据以上计算方法和步骤，对于进口接触位置分别取值为，，， .，，，可得到相应的出口位置的油膜厚度的值为，，，， 110 ，，，。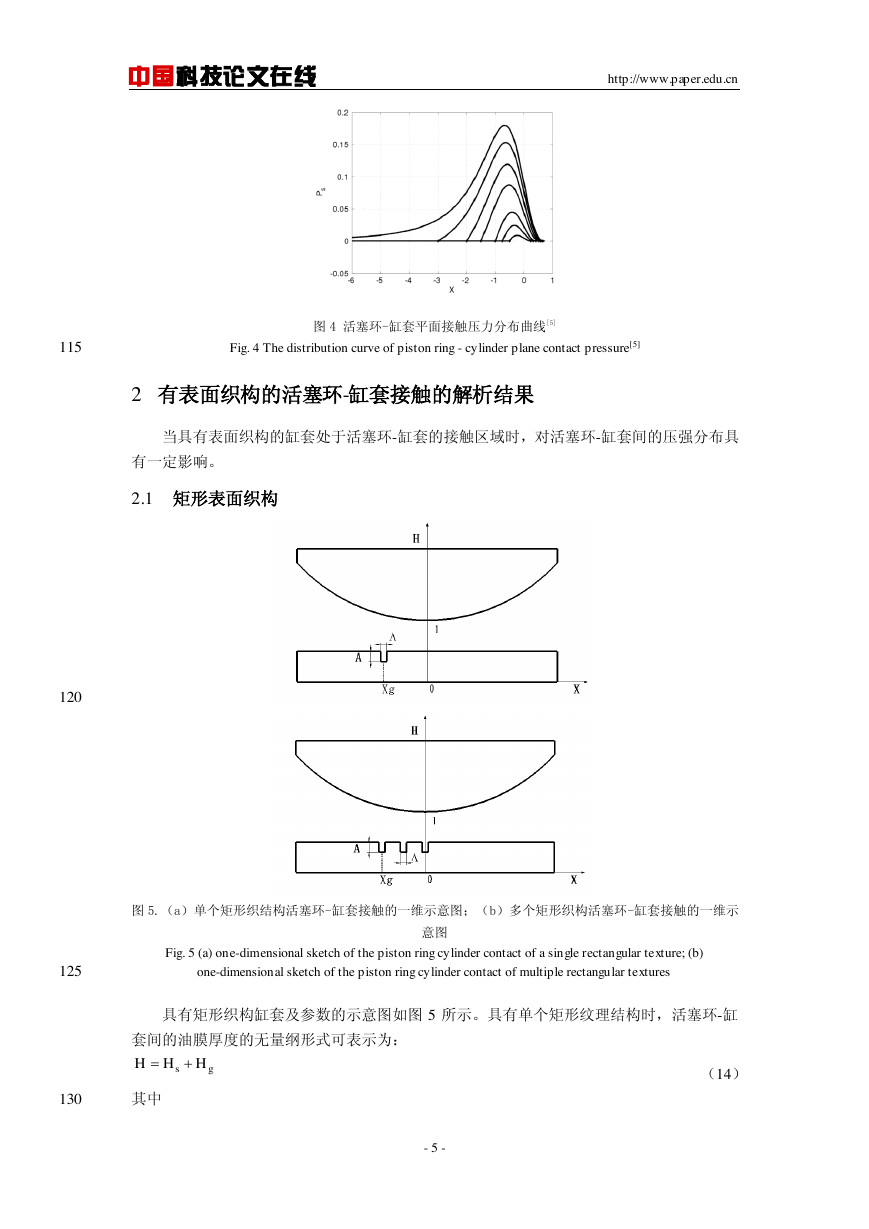活塞环-缸套间的接触压力可由式（11）得出，压力分布曲线如图 4 所示，可以看出，当减少活塞环-缸套平面接触时的润滑油量时，受压区域会变窄，进口和出口接触点位置会向着最小油膜厚度的位置处靠近。 - 4 - aXRaphsonNewton0aXP3HHHHXPbgsaXPbHaX0PbHRaphsonNewtonbH42231112arctanarctan13323bbbbbbZPZYYHHYHHaX325.1175.05.0bH226.1201.1169.1136.1085.1056.1028.1sP0X

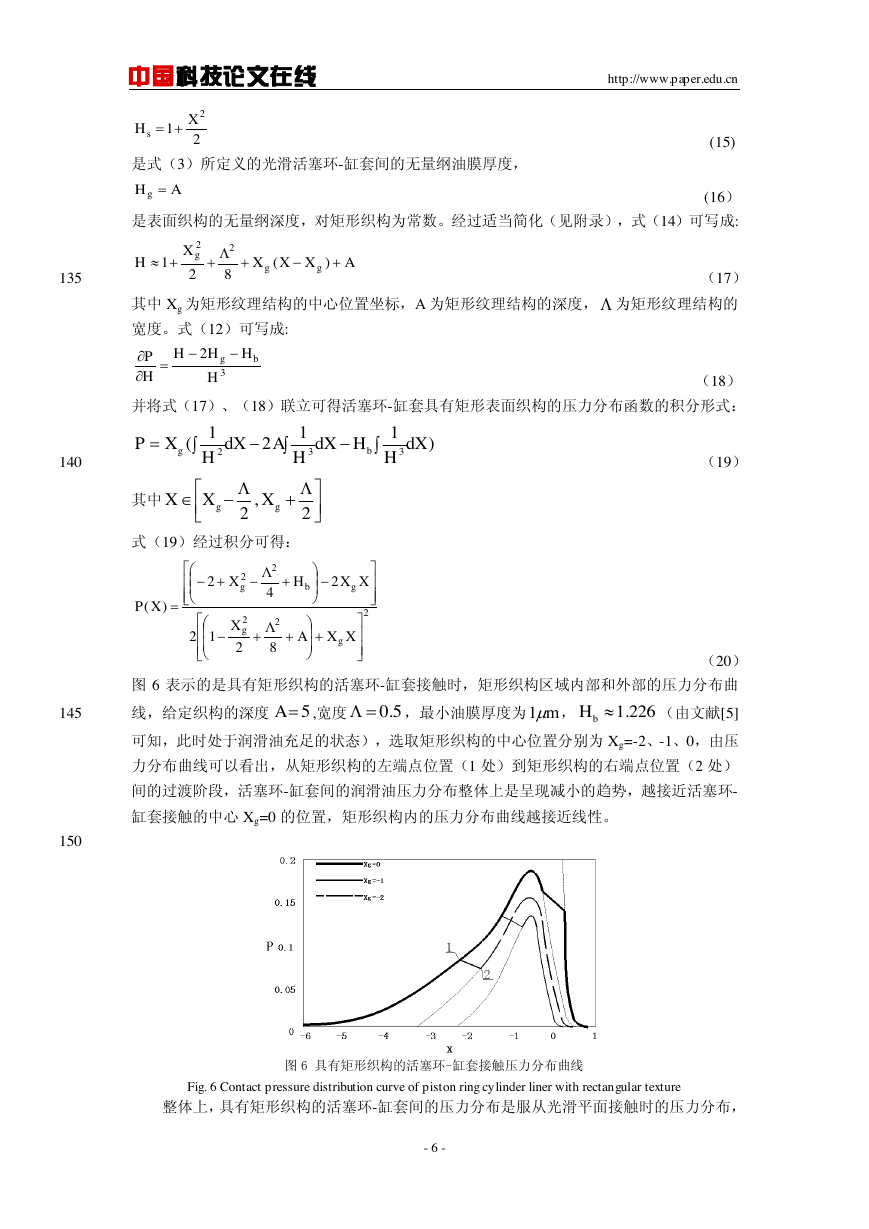
中国科技论文在线 http://www.paper.edu.cn 115 Fig. 4 The distribution curve of piston ring - cylinder plane contact pressure[5] 图 4 活塞环-缸套平面接触压力分布曲线[5] 2 有表面织构的活塞环-缸套接触的解析结果当具有表面织构的缸套处于活塞环-缸套的接触区域时，对活塞环-缸套间的压强分布具有一定影响。 2.1 矩形表面织构 120 图 5.（a）单个矩形织结构活塞环-缸套接触的一维示意图；（b）多个矩形织构活塞环-缸套接触的一维示 Fig. 5 (a) one-dimensional sketch of the piston ring cylinder contact of a single rectangular texture; (b) one-dimensional sketch of the piston ring cylinder contact of multiple rectangular textures 意图 125 具有矩形织构缸套及参数的示意图如图 5 所示。具有单个矩形纹理结构时，活塞环-缸套间的油膜厚度的无量纲形式可表示为：（14） 130 其中 - 5 - gsHHH

中国科技论文在线 http://www.paper.edu.cn (15) 是式（3）所定义的光滑活塞环-缸套间的无量纲油膜厚度， (16）是表面织构的无量纲深度，对矩形织构为常数。经过适当简化（见附录），式（14）可写成: 135 （17）其中 Xg 为矩形纹理结构的中心位置坐标，A 为矩形纹理结构的深度，为矩形纹理结构的宽度。式（12）可写成: （18）并将式（17）、（18）联立可得活塞环-缸套具有矩形表面织构的压力分布函数的积分形式： 140 （19）其中式（19）经过积分可得：图 6 表示的是具有矩形织构的活塞环-缸套接触时，矩形织构区域内部和外部的压力分布曲 145 线，给定织构的深度 ,宽度，最小油膜厚度为，（由文献[5] （20）可知，此时处于润滑油充足的状态），选取矩形织构的中心位置分别为 Xg=-2、-1、0，由压力分布曲线可以看出，从矩形织构的左端点位置（1 处）到矩形织构的右端点位置（2 处）间的过渡阶段，活塞环-缸套间的润滑油压力分布整体上是呈现减小的趋势，越接近活塞环- 缸套接触的中心 Xg=0 的位置，矩形织构内的压力分布曲线越接近线性。 150 图 6 具有矩形织构的活塞环-缸套接触压力分布曲线 Fig. 6 Contact pressure distribution curve of piston ring cylinder liner with rectangular texture 整体上，具有矩形织构的活塞环-缸套间的压力分布是服从光滑平面接触时的压力分布， - 6 - 212XHsAHgAXXXXHggg)(8212232HHHHHPbg233111(2)gbPXdXAdXHdXHHH2,2XXggX222228Λ21224Λ2)(XXAXXXHXXPgggbg5A5.0m1226.1bH

中国科技论文在线 http://www.paper.edu.cn 155 与图 4 类似，只是在矩形织构处出现压力的变化。例如，当矩形织构的中心位置在 Xg=-2 时，在矩形织构的左端点（1 处）左侧是服从光滑平面接触时的压力分布（在图 6 中以实线表示），而在矩形织构的区间内（1 -2 处之间），压力分布出现下降的趋势，这是由于矩形织构区间内的油膜间隙要比矩形织构外的间隙大，导致了油压减小。在矩形织构的右端点（2 处）的右侧，活塞环-缸套间的压力又重新服从光滑平面接触时压力分布（在图 6 中以虚线表示）。 160 需要注意到，与矩形织构起始端（1 处）左边的压力分布相比较，矩形织构的末端（2 处）右侧则是服从不同的光滑平面压力分布。由图 6 可知，矩形织构左侧的压力是服从进口位置 Xa 趋于无穷条件下的光滑平面接触压力分布曲线，而矩形织构右侧的压力则是服从进口接触位置 Xa≈-3.3 条件下的光滑平面接触压力分布曲线。此外，当活塞环-缸套的接触位置越接近中心位置时，活塞环和缸套间的间隙越小，由图 6 可知，此时活塞环-缸套间的压力数 165 值就越大。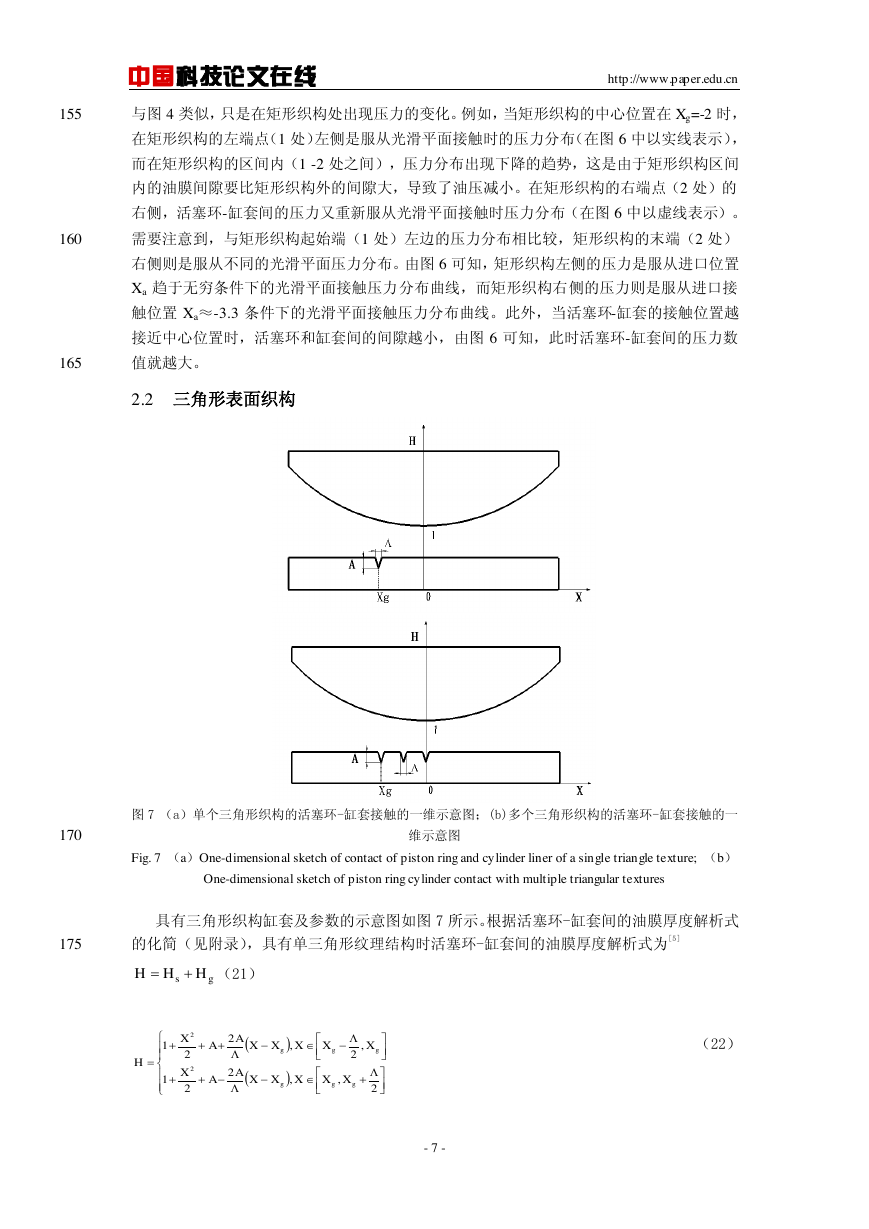 2.2 三角形表面织构图 7 （a）单个三角形织构的活塞环-缸套接触的一维示意图；(b)多个三角形织构的活塞环-缸套接触的一 170 维示意图 Fig. 7 （a）One-dimensional sketch of contact of piston ring and cylinder liner of a single triangle texture; （b） One-dimensional sketch of piston ring cylinder contact with multiple triangular textures 具有三角形织构缸套及参数的示意图如图 7 所示。根据活塞环-缸套间的油膜厚度解析式 175 的化简（见附录），具有单三角形纹理结构时活塞环-缸套间的油膜厚度解析式为[5] （21）（22） - 7 - gsHHH2,,221,2,22122ggggggXXXXXAAXXXXXXAAXH

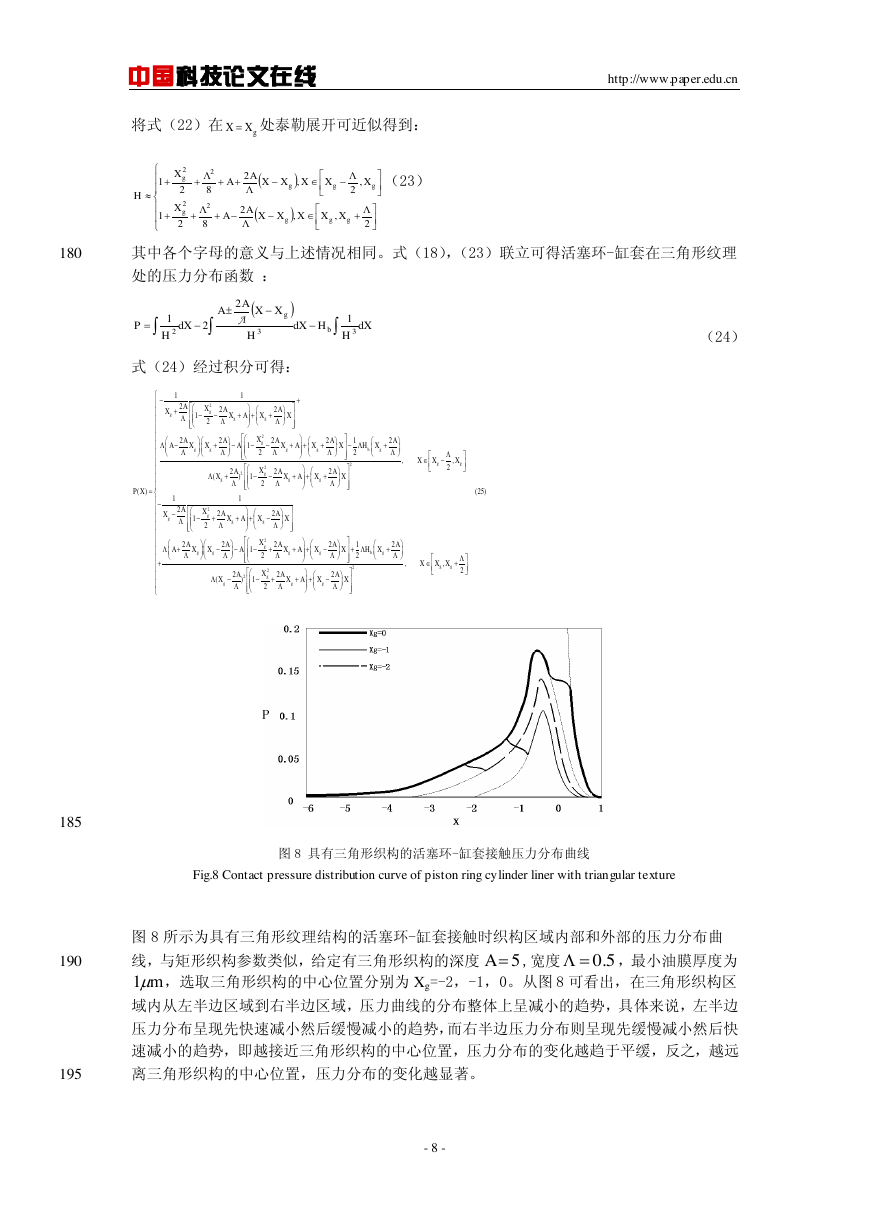
中国科技论文在线 http://www.paper.edu.cn 将式（22）在处泰勒展开可近似得到：（23） 180 其中各个字母的意义与上述情况相同。式（18），（23）联立可得活塞环-缸套在三角形纹理处的压力分布函数：式（24）经过积分可得：（24） 185 190 图 8 具有三角形织构的活塞环-缸套接触压力分布曲线 Fig.8 Contact pressure distribution curve of piston ring cylinder liner with triangular texture 图 8 所示为具有三角形纹理结构的活塞环-缸套接触时织构区域内部和外部的压力分布曲线，与矩形织构参数类似，给定有三角形织构的深度，最小油膜厚度为，选取三角形织构的中心位置分别为 Xg=-2，-1，0。从图 8 可看出，在三角形织构区域内从左半边区域到右半边区域，压力曲线的分布整体上呈减小的趋势，具体来说，左半边 ,宽度压力分布呈现先快速减小然后缓慢减小的趋势，而右半边压力分布则呈现先缓慢减小然后快速减小的趋势，即越接近三角形织构的中心位置，压力分布的变化越趋于平缓，反之，越远 195 离三角形织构的中心位置，压力分布的变化越显著。 - 8 - gXX2Λ,,Λ28Λ21,2Λ,Λ28Λ212222ggggggggXXXXXAAXXXXXXAAXHdXHHdXHXXAAdXHPbg3321221Λ22221122212222212122222()12()gggggggggbgggggAXAAXXAXXXAAAAAAXXAXAXXHXXAAAXXAXXPX22222,,2112221222221212222()12gggggggggggbgggggXXXAXAAXXAXXXAAAAAAXXAXAXXHXXAAXXAX2(25),,22ggXXXAX5A5.0m1

资料库

表面织构对活塞环-缸套接触压力分布影响的理论分析.pdf

相关推荐

开发技术

热门标签

最新资料