2012山东省青岛市中考数学真题及答案.doc-资料库

第1页 / 共12页

第2页 / 共12页

第3页 / 共12页

第4页 / 共12页

第5页 / 共12页

第6页 / 共12页

第7页 / 共12页

第8页 / 共12页

2012 山东省青岛市中考数学真题及答案一、选择题（本题满分 24 分，共有 8 小题，每小题 3 分） 1．（3 分）（2012•青岛）﹣2 的绝对值是（ A．） C． B．﹣2 ﹣ D．2 2．（3 分）（2012•青岛）下列图形中，既是轴对称图形，又是中心对称图形的是（ A． C． B． D．） 3．（3 分）（2012•青岛）如图，正方体表面上画有一圈黑色线条，则它的左视图是（） A． B． C． D． 4．（3 分）（2012•青岛）已知，⊙O1 与⊙O2 的半径分别是 4 和 6，O1O2=2，则⊙O1 与⊙O2 的位置关系是（ A．内切 B．相交 C．外切 D．外离） 5．（3 分）（2012•青岛）某次知识竞赛中，10 名学生的成绩统计如下：分数（分） 60 人数（人） 1 则下列说法正确的是（ A．学生成绩的极差是 4 C．学生成绩的中位数是 80 分 B．学生成绩的众数是 5 D．学生成绩的平均数是 80 分 80 5 90 2 70 1 ） 100 1 6．（3 分）（2012•青岛）如图，将四边形 ABCD 先向左平移 3 个单位，再向上平移 2 个单位，那么点 A 的对应点 A′的坐标是（）

A．（6，1） B．（0，1） C．（0，﹣3） D．（6，﹣3） 7．（3 分）（2012•青岛）用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色．那么可配成紫色的概率是（） A． B． C． D． 8．（3 分）（2012•青岛）点 A（x1，y1），B（x2，y2），C（x3，y3）都是反比例函数的图象上，若 x1＜x2＜0＜x3，则 y1，y2，y3 的大小关系是（ C．y3＜y2＜y1 A．y3＜y1＜y2 B．y1＜y2＜y3 ） D．y2＜y1＜y3 二、填空题（本题满分 18 分，共有 6 道小题，每小题 3 分） 9．（3 分）（2012•青岛）计算：（﹣3）0+ = _________ ． 10．（3 分）（2012•青岛）为改善学生的营养状况，中央财政从 2011 年秋季学期起，为试点地区在校生提供营养膳食补助，一年所需资金约为 160 亿元，用科学记数法表示为 _ 元． 11．（3 分）（2012•青岛）如图，点 A、B、C 在⊙O 上，∠AOC=60°，则∠ABC 的度数是 _________ ． 12．（3 分）（2012•青岛）如图，在一块长为 22 米、宽为 17 米的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分种上草坪，使草坪面积为 300 平方米．若设道路宽为 x 米，则根据题意可列出方程为 _________ ．

13．（3 分）（2012•青岛）如图，Rt△ABC 中，∠ACB=90°，∠ABC=30°，AC=1，将△ABC 绕点 C 逆时针旋转至△A′B′C′，使得点 A′恰好落在 AB 上，连接 BB′，则 BB′的长度为 _________ ． 14．（3 分）（2012•青岛）如图，圆柱形玻璃杯，高为 12cm，底面周长为 18cm，在杯内离杯底 3cm 的点 C 处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿 4cm 与蜂蜜相对的点 A 处，则蚂蚁到达蜂蜜的最短距离为 _________ cm．三、作图题（本题满分 4 分）用圆规、直尺作图，不写作法，但要保留作图痕迹． 15．（4 分）（2012•青岛）已知：线段 a，c，∠α．求作：△ABC．使 BC=a，AB=c，∠ABC=∠α．结论：

四、解答题（本题满分 74 分，共有 9 道小题） 16．（8 分）（2012•青岛）（1）化简：（2）解不等式组：． 17．（6 分）（2012•青岛）某校为开展每天一小时阳光体育活动，准备组建篮球、排球、足球、乒乓球四个兴趣小组，并规定每名学生至少参加 1 个小组，也可兼报多个小组．该校对八年级全体学生报名情况进行了抽样调查，并将所得数据制成如下两幅统计图：根据图中的信息解答下列问题：（1）补全条形统计图；（2）若该校八年级共有 400 名学生，估计报名参加 2 个兴趣小组的人数；（3）综合上述信息，谈谈你对该校即将开展的兴趣小组活动的意见和建议．（字数不超过 30 字） 18．（6 分）（2012•青岛）某商场为了吸引顾客，举行抽奖活动，并规定：顾客每购买 100 元的商品，就可随机抽取一张奖券，抽得奖券“紫气东来”、“花开富贵”、“吉星高照”，就可以分别获得 100 元、50 元、20 元的购物券，抽得“谢谢惠顾”不赠购物券；如果顾客不愿意抽奖，可以直接获得购物券 10 元．小明购买了 100 元的商品，他看到商场公布的前 10000 张奖券的抽奖结果如下：花开富贵奖券种类出现张数（张） 500 1000 （1）求“紫气东来”奖券出现的频率；（2）请你帮助小明判断，抽奖和直接获得购物卷，哪种方式更合算？并说明理由．吉星高照 2000 紫气东来谢谢惠顾 6500 19．（6 分）（2012•青岛）小丽乘坐汽车从青岛到黄岛奶奶家，她去时经过环湾高速公路，全程约 84 千米，返回时经过跨海大桥，全程约 45 千米．小丽所乘汽车去时的平均速度是返回时的 1.2 倍，所用时间却比返回时多 20 分钟．求小丽所乘汽车返回时的平均速度．

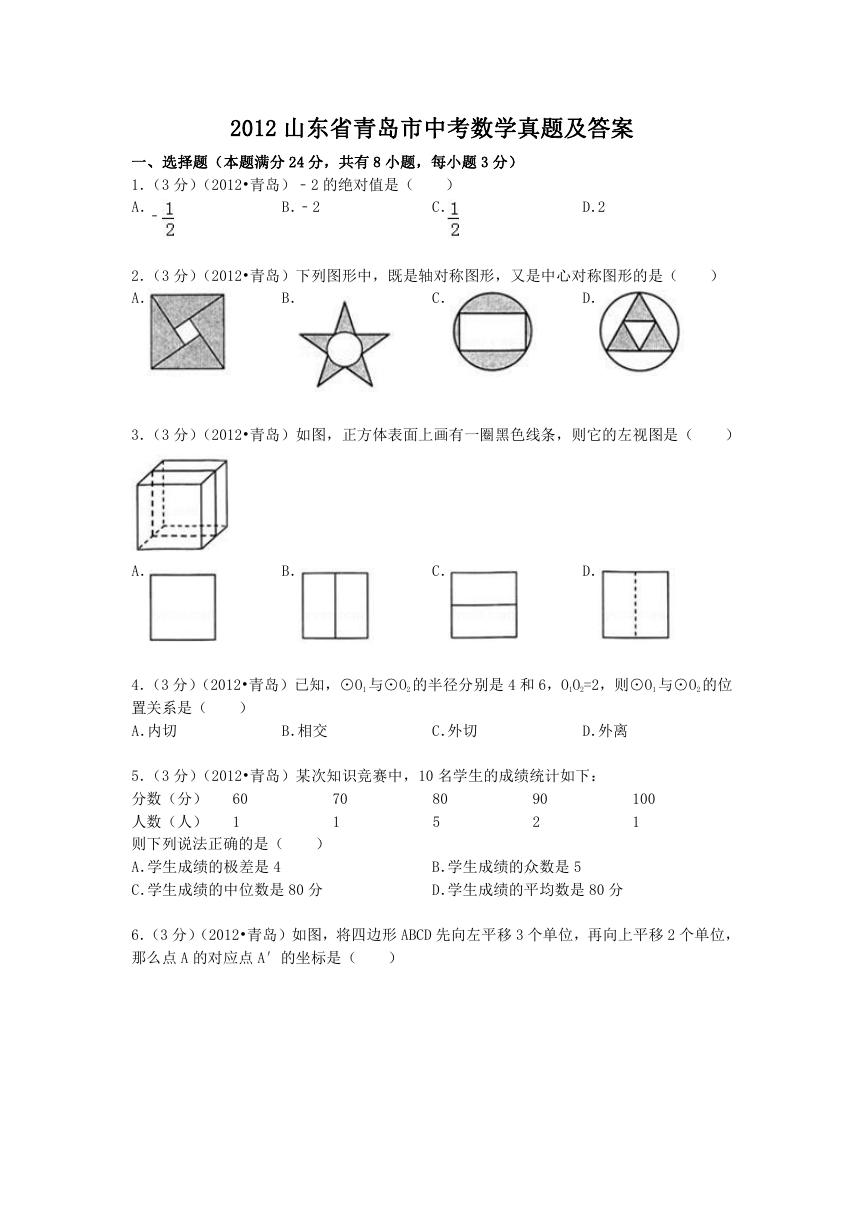
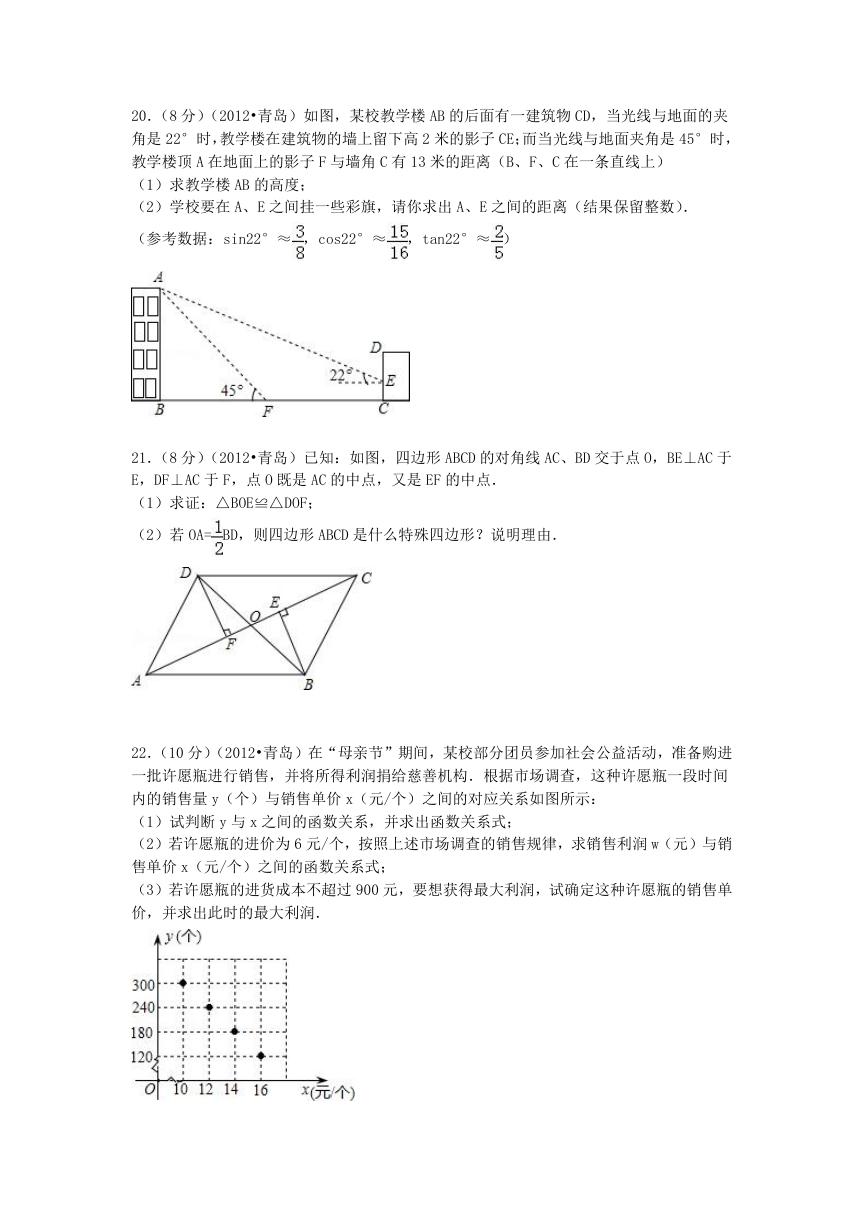
20．（8 分）（2012•青岛）如图，某校教学楼 AB 的后面有一建筑物 CD，当光线与地面的夹角是 22°时，教学楼在建筑物的墙上留下高 2 米的影子 CE；而当光线与地面夹角是 45°时，教学楼顶 A 在地面上的影子 F 与墙角 C 有 13 米的距离（B、F、C 在一条直线上）（1）求教学楼 AB 的高度；（2）学校要在 A、E 之间挂一些彩旗，请你求出 A、E 之间的距离（结果保留整数）．（参考数据：sin22°≈ ，cos22°≈ ，tan22°≈ ） 21．（8 分）（2012•青岛）已知：如图，四边形 ABCD 的对角线 AC、BD 交于点 O，BE⊥AC 于 E，DF⊥AC 于 F，点 O 既是 AC 的中点，又是 EF 的中点．（1）求证：△BOE≌△DOF；（2）若 OA= BD，则四边形 ABCD 是什么特殊四边形？说明理由． 22．（10 分）（2012•青岛）在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量 y（个）与销售单价 x（元/个）之间的对应关系如图所示：（1）试判断 y 与 x 之间的函数关系，并求出函数关系式；（2）若许愿瓶的进价为 6 元/个，按照上述市场调查的销售规律，求销售利润 w（元）与销售单价 x（元/个）之间的函数关系式；（3）若许愿瓶的进货成本不超过 900 元，要想获得最大利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润．

23．（10 分）（2012•青岛）问题提出：以 n 边形的 n 个顶点和它内部的 m 个点，共（m+n）个点作为顶点，可把原 n 边形分割成多少个互不重叠的小三角形？问题探究：为了解决上面的问题，我们将采取一般问题特殊性的策略，先从简单和具体的情形入手：探究一：以△ABC 的三个顶点和它内部的 1 个点 P，共 4 个点为顶点，可把△ABC 分割成多少个互不重叠的小三角形？如图①，显然，此时可把△ABC 分割成 3 个互不重叠的小三角形．探究二：以△ABC 的三个顶点和它内部的 2 个点 P、Q，共 5 个点为顶点，可把△ABC 分割成多少个互不重叠的小三角形？在探究一的基础上，我们可看作在图①△ABC 的内部，再添加 1 个点 Q，那么点 Q 的位置会有两种情况：一种情况，点 Q 在图①分割成的某个小三角形内部．不妨假设点 Q 在△PAC 内部，如图②；另一种情况，点 Q 在图①分割成的小三角形的某条公共边上．不妨假设点 Q 在 PA 上，如图 ③．显然，不管哪种情况，都可把△ABC 分割成 5 个不重叠的小三角形．探究三：以△ABC 的三个顶点和它内部的 3 个点 P、Q、R，共 6 个点为顶点可把△ABC 分割成 _________ 个互不重叠的小三角形，并在图④中画出一种分割示意图．探究四：以△ABC 的三个顶点和它内部的 m 个点，共（m+3）个顶点可把△ABC 分割成 _________ 个互不重叠的小三角形．探究拓展：以四边形的 4 个顶点和它内部的 m 个点，共（m+4）个顶点可把四边形分割成 _________ 个互不重叠的小三角形．问题解决：以 n 边形的 n 个顶点和它内部的 m 个点，共（m+n）个顶点可把△ABC 分割成 _________ 个互不重叠的小三角形．实际应用：以八边形的 8 个顶点和它内部的 2012 个点，共 2020 个顶点，可把八边形分割成多少个互不重叠的小三角形？（要求列式计算） 24．（12 分）（2012•青岛）已知：如图，在 Rt△ABC 中，∠C=90°，AC=6cm，BC=8cm，D、E 分别是 AC、AB 的中点，连接 DE，点 P 从点 D 出发，沿 DE 方向匀速运动，速度为 1cm/s；同时，点 Q 从点 B 出发，沿 BA 方向匀速运动，速度为 2cm/s，当点 P 停止运动时，点 Q 也停止运动．连接 PQ，设运动时间为 t（s）（0＜t＜4）．解答下列问题：（1）当 t 为何值时，PQ⊥AB？（2）当点 Q 在 BE 之间运动时，设五边形 PQBCD 的面积为 y（cm2），求 y 与 t 之间的函数关系式；

（3）在（2）的情况下，是否存在某一时刻 t，使 PQ 分四边形 BCDE 两部分的面积之比为 S △PQE：S 四边形 PQBCD=1：29？若存在，求出此时 t 的值以及点 E 到 PQ 的距离 h；若不存在，请说明理由．

2012 年山东省青岛市中考数学试卷参考答案与试题解析 5．C 6．B 3．B 4．A 一、选择题 1．D 2．C 二、填空题（本题满分 18 分，共有 6 道小题，每小题 3 分）请将 9--14 各小题的答案填写在第 14 小题后面给出的表格相应位置上． 9．7．10．1.6×1010．11．150°．12．（22﹣x）（17﹣x）=300．13．．14．5 四、解答题（本题满分 74 分，共有 9 道小题） 7． D 8． A ． 16．解：（1）原式= = …4 分解：（2）解不等式①，x＞，解不等式②，x≤4， ∴原式不等式组的解集为＜x≤4． 17．解：（1）∵从统计图知报名参加丙小组的有 15 人，占总数的 30% ∴总人数有 15÷30%=50 人， ∴报名参加丁小组的有 50﹣10﹣20﹣15=5 人，统计图为：（2）报名参加 2 个兴趣小组的有 400× =160 人（3）合理即可：如：利用课余时间多参加几个兴趣小组． 18．解：（1）或 5%；（2）平均每张奖券获得的购物券金额为 +0× =14（元） ∵14＞10 ∴选择抽奖更合算． 19．解：设小丽所乘汽车返回时的平均速度是 x 千米/时，根据题意得：

资料库

2012山东省青岛市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料