2017C题颜色与物质浓度的辨识问题——倪永亮等（南京铁道职业技术学院，专科组MATLAB 创新奖获得者）.pdf-资料库

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第1页.png

第1页 / 共31页

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第2页.png

第2页 / 共31页

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第3页.png

第3页 / 共31页

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第4页.png

第4页 / 共31页

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第5页.png

第5页 / 共31页

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第6页.png

第6页 / 共31页

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第7页.png

第7页 / 共31页

9607006d-9c18-49ba-bfb4-217f2d56401c.pdf-第8页.png

第8页 / 共31页

颜色与物质浓度的辨识问题摘要本文是对颜色与物质浓度的辨识问题的研究，通过对溶液色度值与待测物浓度的实验数据进行多元回归分析，建立了线性和非线性回归方程模型，给出了数据的评价准则和模型的误差分析。问题一：首先依据对数据初步分析，发现物质浓度与颜色读数存在着一定的关系。利用 MATLAB 统计工具箱中的 Regress 函数求出回归系数和置信区间，并进行残差分析，最终建立关于颜色读数和物质浓度的多元线性回归模型。基于对模型的检验分析的基础上，给出了判别数据优劣的五大准则，分别是评估模型是否成功的四个要素，检验、相关系数、值、估计误差方差；再加上数据完整性要素，即模型拟合过程中是否存在异常数据剔除。根据判别准则，数据优劣的排序为：组胺>溴酸钾>奶中尿素>硫酸铝钾>工业碱。问题二：首先建立二氧化硫浓度与颜色读数之间的线性回归模型，模型的残差较大，拟合效果不佳。考虑建立非线性二次回归模型，利用 MATLAB 统计工具箱中的 rstool 函数建模，通过剩余标准差和残差评估模型优劣。最终建立的非线性二次回归模型中，剩余标准差很小，预测模型非常好，模型的残差相比五元线性回归模型降低了一个数量级，因此线性二次回归模型比线性回归模型更优。问题三：首先降低多元线性回归模型中颜色的维度来分析颜色维度对模型的影响；然后再通过减少数据量来分析数据量对模型的影响。通过分析发现：数据量不能低于 6,一般在 10-15 之间；颜色纬度可以降低，二纬和三纬都可以，一纬模型就不太优甚至不成立了，而且颜色维度的大小比数据量的多少对模型的影响更大；于是最后使用层次分析法对数据量的多少和颜色维度的大小对模型的影响因子进行分析求解，得出了影响因子分别为 0.414 和 0.586。关键词：多元线性回归，多元非线性二次回归，MATLAB，误差，层次分析法 1 F2RP2S

问题重述（一）问题的背景：比色法是目前常用的一种检测物质浓度的方法，即把待测物质制备成溶液后滴在特定的白色试纸表面，等其充分反应以后获得一张有颜色的试纸，再把该颜色试纸与一个标准比色卡进行对比，就可以确定待测物质的浓度档位了。由于每个人对颜色的敏感差异和观测误差，使得这一方法在精度上受到很大影响。随着照相技术和颜色分辨率的提高，希望建立颜色读数和物质浓度的数量关系，即只要输入照片中的颜色读数就能够获得待测物质的浓度。试根据附件所提供的有关颜色读数和物质浓度数据完成下列问题：（二）问题的提出： 1.附件 Data1.xls 中分别给出了 5 种物质在不同浓度下的颜色读数，讨论从这 5 组数据中能否确定颜色读数和物质浓度之间的关系，并给出一些准则来评价这 5 组数据的优劣。 2.对附件 Data2.xls 中的数据，建立颜色读数和物质浓度的数学模型，并给出模型的误差分析。 3.探讨数据量和颜色维度对模型的影响。二、模型假设与符号说明 1．模型假设 1）反应应具有较高的灵敏度和选择性； 2）反应生成的有色化合物的组成恒定且较稳定； 3）选择适当的显色反应和控制好适宜的反应条件。 2．符号说明：见表 1 符号含义单位 F P 各待测物理论浓度 (i=1,2,3,4,5,6) 各待测物实际浓度 (i=1,2,3,4,5,6) 回归方程回归系数残差相关系数 F 值与 F 对应的概率估计误差方差 2 iY/ppmmgLiY/ppmmgLCr2R2S

B G R H S 蓝色颜色值绿色颜色值红色颜色值色调饱和度数据量表 1 符号说明三、问题的分析首先对 Data1.xls 和 Data2.xls 提供的数据利用 MATLAB 进行相关性分析发现：颜色读数（五个维度：B,G,R,H,S）对物质浓度呈现一定线性相关性，而这一结论与文献[1]使用朗博-比尔吸收定律得到的结论一致。即物质浓度和颜色读数之间存在一定的关系。其次利用统计学中的多元回归[2]对给出的六组数据进行回归分析，从而得出物质浓度与颜色读数（五维）之间的相互关系，确定它们之间合适的数学表达式（或数学模型）即经验公式或回归方程。针对问题一基于对 Data1.xls 的数据分析，我们可以利用 MATLAB 统计工具箱中的 Regress 函数求出回归系数和置信区间，绘出残差图并进行残差分析，剔除置信区间不包含零点的异常点数据，重新进行多元线性回归，能够更好地建立关于颜色读数和物质浓度的多元线性回归模型。基于对模型的检验分析的基础上，可以考虑评估模型是否成功的四个要素，检验、相关系数、值、估计误差方差 ,相关系数越接近 1，说明回归方程越显著；时拒绝，越大，说明回归方程越显著；与对应的概率时拒绝，回归模型成立。估计误差方差越小，回归方程越显著。还可以再考虑数据完整性要素，即模型拟合过程中是否存在异常数据剔除。给出对应评价 Data1.xls 中 5 组数据优劣的五大准则，并根据 5 组数据是否同时满足五大准则对其优劣进行判别。针对问题二问题二是在问题一的基础上，进一步确定颜色读数和物质浓度的数学模型- 线性回归方程。首先建立二氧化硫浓度与颜色读数之间的线性回归模型，模型的残差较大，拟合效果不佳。考虑建立非线性二次回归模型，利用 MATLAB 统计工具箱中的 rstool 函数建 3 mF2RP2S2R1(,1)FFknk0HFFP0H

模，通过剩余标准差和残差评估模型优劣。最终建立的非线性二次回归模型中，剩余标准差很小，预测模型非常好，模型的残差相比多元线性回归模型降低了一个数量级，因此线性二次回归模型比线性回归模型更优。通过两种模型的误差的对比发现：非线性回归二次方程的精度更高。针对问题三问题三是讨论数据量和颜色维度对模型的影响。根据问题一和问题二的求解结果发现：数据量的大小会影响模型的优劣；以及通过枚举法调整线性回归中变量的数量即颜色维度发现：颜色维度的多少也会影响模型的优劣。而且数据量对模型优劣的影响度大于颜色维度对模型优劣的影响度。因此本文提出采用层次分析法对两者的影响因子进行分析，最终得出了数据量和颜色维度对模型优劣的影响因子。问题一：四、模型的建立与求解基于对数据的分析，本文认为有 Data1.xls 提供的 5 组数据能确定颜色读数与物质浓度之间的关系，并建立了多元线性回归模型：（Ⅰ）（Ⅰ）式中 , , , , 表示方程的回归系数。利用 matlab 统计工具箱建立多元线性回归方程： [b, bint,r,rint,stats]=regress(Y,X,alpha)（Ⅱ）式（Ⅱ）中 b 为回归系数，bint 为回归系数的置信区间，r 为残差，rint 为残差的置信区间，alpha 为显著性水平。stats 包含四个统计量，相关系数、F 值、与 F 对应的概率 p，估计误差方差。相关系数越接近 1，说明回归方程越显著；时拒绝，F 越大，说明回归方程越显著；与 F 对应的概率时拒绝，回归模型成立。估计误差方差越小，回归方程越显著。 1.组胺浓度与颜色读数之间的关系函数：根据组胺的实验数据（见表 2），其中 0 表示待测物质浓度为零的情形，即水溶液，使用 matlab 对数据进行多元线性回归（代码见附录中程序 1），画出残差图（图 1）并给出具体的残差值（表 3）和其置信区间（表 4）。浓度（ppm） B 0 100 50 68 37 46 G 110 66 87 4 R 121 110 117 H 23 12 16 S 111 169 155 12345YCRCGCBCHCS1C2C3C4C5C2R2R1(,1)FFknk0Hp0H

25 12.5 0 100 50 25 12.5 62 66 65 35 46 60 64 99 102 110 64 87 99 101 表 2 组胺的实验数据 120 118 120 109 118 120 118 19 20 24 11 16 19 20 122 112 115 172 153 126 115 图 1 组胺浓度与颜色读数线性回归残差图浓度（ppm）残差值 r 0 100 50 25 12.5 0 100 50 25 12.5 -0.993129343227508 -0.083240562564029 -0.184054282892987 -0.087070619285910 0.920198815901770 0.733366635833562 0.141799543614084 -0.222352920091282 1.056506552856305 -1.282023820143920 相关系数表 3 组胺浓度与颜色读数线性回归残差值 F 值与 F 对应的概率估计误差方差 P 0.999580110101 1904.461358300401 0.000000771022 1.312155935514 表 4 由表 4：相关系数 =0.999580110101，说明回归方程非常显著。F 对应的概率，拒绝，根据 F 检验，回归模型（Ⅲ）成立。 5 2R2Rp0H

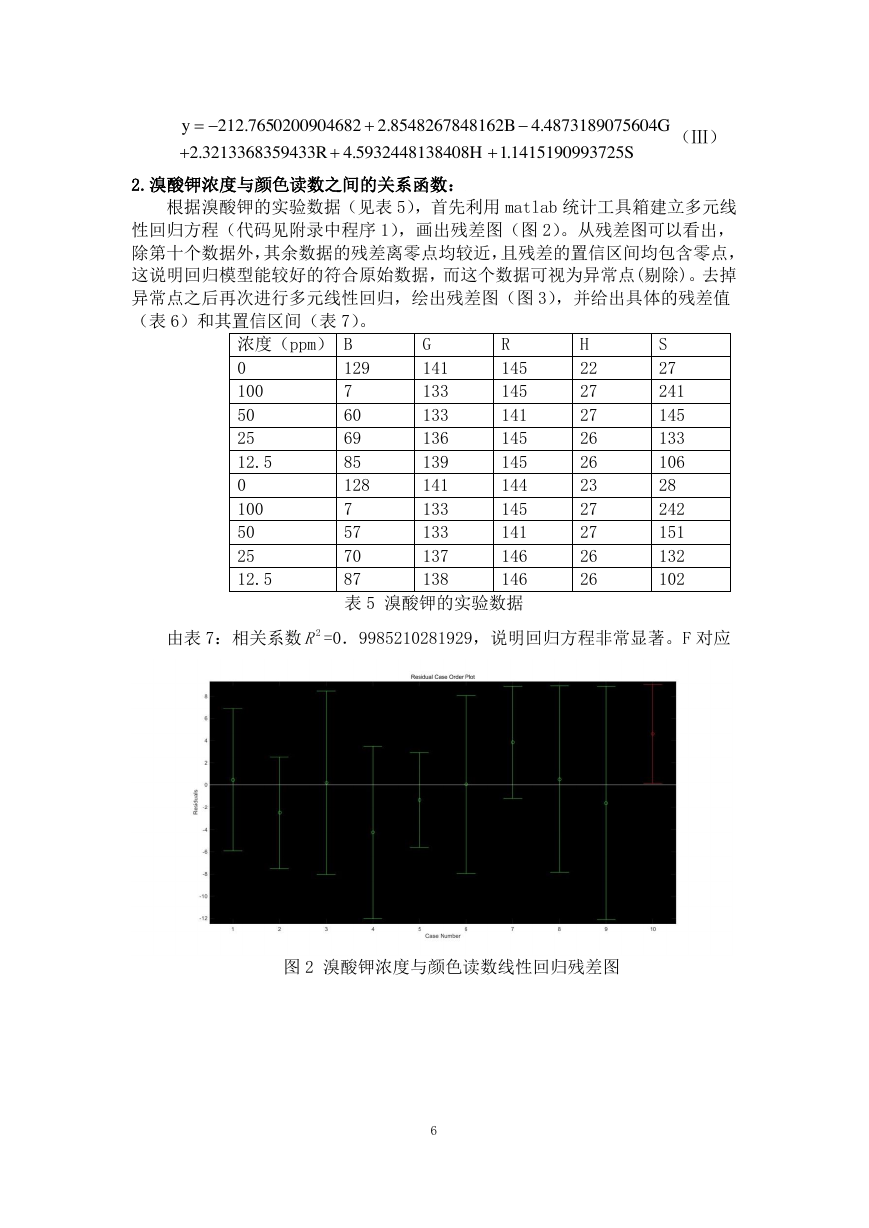
（Ⅲ） 2.溴酸钾浓度与颜色读数之间的关系函数：根据溴酸钾的实验数据（见表 5），首先利用 matlab 统计工具箱建立多元线性回归方程（代码见附录中程序 1），画出残差图（图 2）。从残差图可以看出，除第十个数据外，其余数据的残差离零点均较近，且残差的置信区间均包含零点，这说明回归模型能较好的符合原始数据，而这个数据可视为异常点(剔除)。去掉异常点之后再次进行多元线性回归，绘出残差图（图 3），并给出具体的残差值（表 6）和其置信区间（表 7）。浓度（ppm） B 0 100 50 25 12.5 0 100 50 25 12.5 R 145 129 145 7 141 60 145 69 145 85 144 128 145 7 141 57 146 70 87 146 表 5 溴酸钾的实验数据 G 141 133 133 136 139 141 133 133 137 138 H 22 27 27 26 26 23 27 27 26 26 S 27 241 145 133 106 28 242 151 132 102 由表 7：相关系数 =0．9985210281929，说明回归方程非常显著。F 对应图 2 溴酸钾浓度与颜色读数线性回归残差图 6 212.76502009046822.85482678481624.48731890756042.32133683594334.59324481384081.1415190993725yBGRHS2R

图 3 剔除异常点后溴酸钾浓度与颜色读数线性回归残差图浓度（ppm） 0 100 50 25 12.5 0 100 50 25 残差值 r -0.311054621479073 -1.739298695133584 1.198950353741111 -2.046358165775416 -0.633956401784815 0.563887602493494 1.832705601078601 -0.844912938120160 1.980037264978989 表 6 相关系数 F 值与 F 对应的概率 P 估计误差方差 0．9985210281929 405．0872464611553 0.0001928592100 5.8200279444505 表 7 的概率，拒绝，根据 F 检验，回归模型（Ⅳ）成立。（Ⅳ） 3．工业碱浓度与颜色读数之间的函数关系：根据工业碱的实验数据（见表 8），使用 matlab 对数据进行多元线性回归（代码见附录中程序 1），画出残差图（图 4）并给出具体的残差值（表 9）和其置信区间（表 10）。浓度（ppm） B 7.34 8.14 8.74 153 151 158 G 140 142 126 R 132 133 127 7 H 108 104 120 S 35 29 52 2Rp0H1309.8324252141507.825296356378+4.9494079801104.7225113506989.8507456348373.572004296212yBGRHS

9.19 10.18 11.8 0 161 127 94 152 85 21 6 142 118 119 91 132 132 147 148 105 表 8 工业碱的实验数据 120 211 237 32 图 4 工业碱浓度与颜色读数线性回归残差图浓度（ppm）残差值 r 7.34 8.14 8.74 9.19 10.18 11.8 0 3.193187385650077 1.630046034029125 -0.845684659598861 0.362126613702886 -0.206897864646130 0.084838267818999 -4.217615776955910 表 9 相关系数 F 值与 F 对应的概率 P 估计误差方差 0.631383991895078 0.342570033863204 0.851764320877558 31.538101080870671 表 10 由表 10：相关系数 =0.631383991895078，说明回归方程不显著。根据 F 检验，F 对应的概率，接受，回归模型（Ⅴ）不成立。（Ⅴ） 4．硫酸铝钾浓度与颜色读数之间的函数关系：根据硫酸铝钾的实验数据（见表 11），使用 matlab 对数据进行多元线性回归（代码见附录中程序 1），画出残差图（图 5）。浓度（ppm） B 0 0 116 114 G 126 126 R 104 104 8 H 76 74 S 44 45 2R2Rp0H261.06486974071350.16421293824671.39816940939730.31364160779600.13058109229480.8798705475876yBGRHS

资料库

2017C题颜色与物质浓度的辨识问题——倪永亮等（南京铁道职业技术学院，专科组MATLAB 创新奖获得者）.pdf

相关推荐

课程资源

热门标签

最新资料