2020年广东暨南大学材料力学考研真题.doc

发布时间：2022-09-15 发布人：admin 分类：说明书资料大小：0.24M 资料格式：doc 举报版权申诉

第1页 / 共5页

第2页 / 共5页

第3页 / 共5页

第4页 / 共5页

第5页 / 共5页

文本预览

2020 年广东暨南大学材料力学考研真题招生专业与代码：一般力学与力学基础、工程力学、固体力学、结构工程考试科目名称及代码：材料力学 819 考生注意：所有答案必须写在答题纸（卷）上，写在本试题上一律不给分。一、填空题（共 5 小题，每小题 2 分，共 10 分） 1-1．若将等截面实心圆直杆的直径增加一倍，其它条件不变，则其扭转刚度是原来的倍。 1-2．两根承受轴向拉伸的杆件均在线弹性范围内，一为钢杆弹性模量 E1=210GPa，另一为铸铁弹性模量 E2=100GPa 。若两杆的正应力相等，则两杆的纵向线应变的比值为；若两杆的纵向应变相同，则两杆的正应力的比值为。 1-3．如题 1-3 图所示，在板状试件表面贴两片应变片，在集中力 P 作用下平行轴线的应变片 1 120 10   6   ，垂直轴线的应变片  2    6 40 10  ；那么试件泊松比为。 1-4．如题 1-4(a)图、题 1-4(b)图单元体中，实线代表变形前，虚线代表变形后，题 1-4(a) 图角应变为为弧度) ，题 1-4(b) 图角应变为。(图中角度 1-5．矩形截面柱如题 1-5 图所示，F1 的作用线与柱的中心轴线重合，F2 作用在 y 轴上，F2 与柱 z轴线距离为 e；立柱的 m-m截面b h 上最大压应力是。

二、单项选择题（共 5 小题，每小题 2 分，共 10 分）题 1-5 图 2-1．各向同性假设材料沿各个方向具有相同的。 (A) 力学性质 (B) 外力 (C) 变形 (D) 位移 2-2．空心圆截面直杆的外径为 D、内径为 d，在计算扭转最大剪应力时需要确定扭转截面系数 WP，其表达式以下正确的是。 (A)  3D 16  (B) 3 d 16 (C)  16D  4（D  d 4   ） (D)   3（D 16  d 3  ） 2-3．非圆截面杆自由扭转时，横截面上。 (A) 只有切应力，没有正应力 (B) 只有正应力，没有切应力 (C) 既有正应力又有切应力 (D) 正应力、切应力均为零 2-4. 梁在集中力作用的截面处，它的内力图。 (A) 剪力 FS 图突变、弯矩 M 图光滑连续 (B) 剪力 FS 图突变、弯矩 M 图转折 (C) 弯矩 M 图突变、剪力 FS 图光滑连续 (D) 弯矩 M 图突变、剪力 FS 图转折 2-5．对于拉伸强度低于剪切强度的铸铁等脆性材料圆杆，扭转破坏是由 45o 斜截面上的引起。 (A) 最大拉应力 (B) 最大压应力 (C) 最大剪应力 (D) 都有可能三、简答题（共 5 小题，共 40 分） 3-1．一根等截面直杆受力如题 3-1 图所示，已知杆的横截面面积 A和材料的弹性模量 E。(1) 作轴力图； (2) 求杆轴线上 B点的位移ΔB 、C点的位移ΔC 及 D点的位移 ΔD 。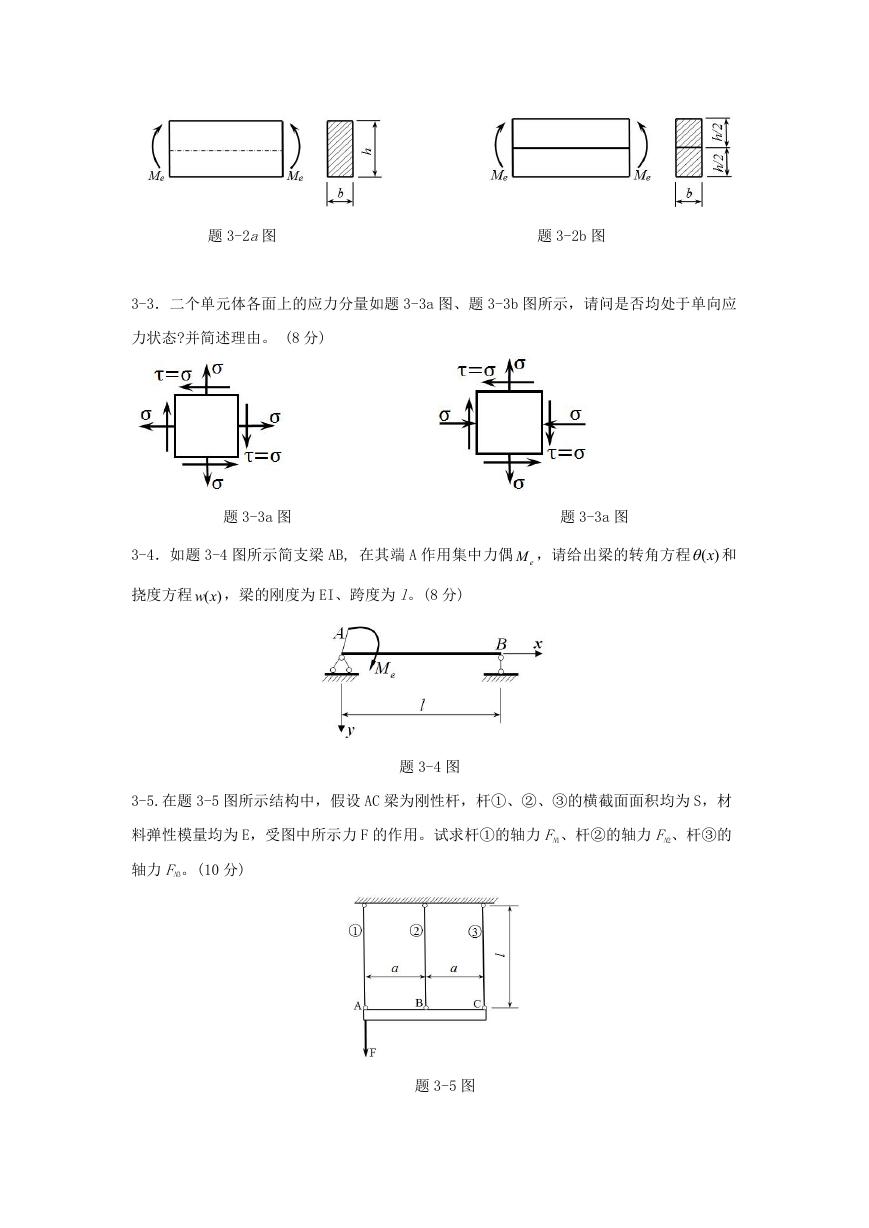(8 分) 题 3-1 图 3-2．一矩形截面b h 的等直梁，两端承受外力偶矩 Me (如题 3-2a图)。已知梁的中性层上 hb 的梁，将两梁仍叠合在一起，并承受相无应力，若将梁沿中性层锯开成为两根截面为 2 同外力偶矩 Me (如题 3-2b 图)。试问：为什么锯开前、后，两者的工作情况不同？锯开后，可采取什么措施以保证其工作状态不变。 (6 分)

题 3-2a图题 3-2b 图 3-3．二个单元体各面上的应力分量如题 3-3a 图、题 3-3b 图所示，请问是否均处于单向应力状态?并简述理由。 (8 分) 题 3-3a 图题 3-3a 图 3-4．如题 3-4 图所示简支梁 AB, 在其端 A 作用集中力偶 eM ，请给出梁的转角方程 ( )x 和挠度方程 ( )w x ，梁的刚度为 EI、跨度为 l。(8 分) 题 3-4 图 3-5.在题 3-5 图所示结构中，假设 AC 梁为刚性杆，杆①、②、③的横截面面积均为 S，材料弹性模量均为 E，受图中所示力 F 的作用。试求杆①的轴力 FN1、杆②的轴力 FN2、杆③的轴力 FN3。(10 分) 题 3-5 图

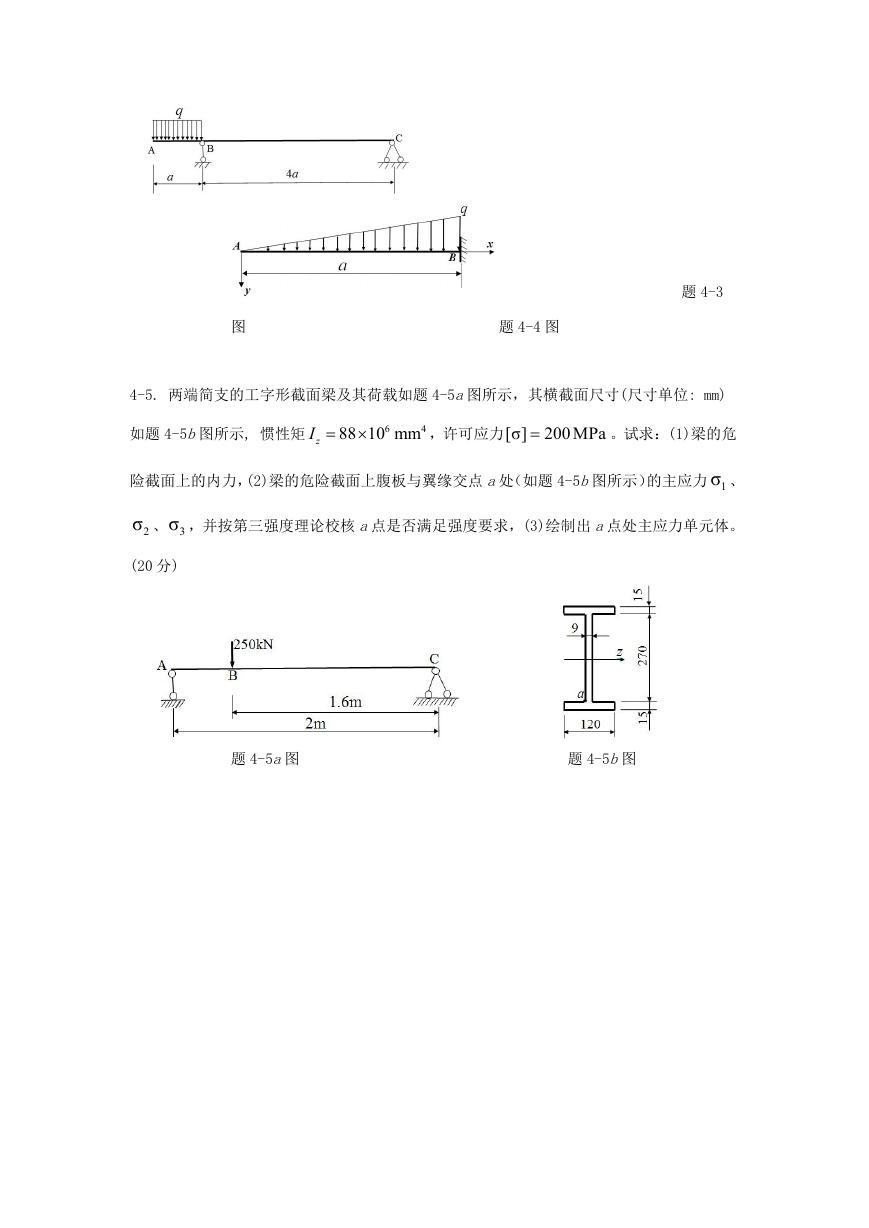
四、计算题（共 5 小题，共 90 分） 4-1. 如题 4-1 图所示支架，圆截面斜撑杆 AB 直径 d=40mm，弹性模量 E=200GPa，比例极限 p =240MPa，稳定安全因素 nst=2，试根据杆 AB 的稳定性确定许可载荷[F]。(15 分) 题 4-1 图 4-2．如题 4-2 图所示，实心圆轴 AB 的直径 d=100mm，长 l=1m，其两端所受外力偶矩Ｍe=14kN·m，材料的切变模量 G=80GPa。请求：(1)最大切应力及两端截面间的相对扭转角；(2)如题 4-2 图所示 C 截面上 D、Ｅ、Ｆ三点处切应力的大小及其方向(请在图中标出三点应力方向)，点 D、Ｅ在外圆周上，点Ｆ距离圆心 O 为 25mm；(3) C 截面上点 D、Ｅ、Ｆ处的切应变。(20 分) 题 4-2 图 4-3.已知题 4-3 图所示外伸简支梁的均布载荷 q 和尺寸 a。试求：(1)梁的支座反力，(2)建立梁的剪力方程 ( ) SF x 和弯曲方程 ( )M x ，(3) 作剪力图和弯矩图。(20 分) 4-4.弯曲刚度为 EI 的悬臂梁受三角形分布荷载如题 4-4 图所示，其中 q、a 为已知量。梁的材料为线弹性体且不计切应变对挠度的影响。试计算悬臂梁自由端 A 的转角θ A 、梁自由端 A 的垂直位移 Ayw 。(15 分)

图题 4-4 图题 4-3 4-5. 两端简支的工字形截面梁及其荷载如题 4-5a图所示，其横截面尺寸(尺寸单位: mm) 如题 4-5b图所示, 惯性矩 zI  88 10 mm  6 4 ，许可应力[σ] 200MPa  。试求：(1)梁的危险截面上的内力，(2)梁的危险截面上腹板与翼缘交点 a处（如题 4-5b图所示）的主应力 1σ 、 2σ 、 3σ ，并按第三强度理论校核 a点是否满足强度要求，(3)绘制出 a点处主应力单元体。 (20 分) 题 4-5a图题 4-5b图

分享到：

赞收藏

资料库

2020年广东暨南大学材料力学考研真题.doc

相关推荐

考研

热门标签

最新资料