《计算机图形学》教案.doc-资料库

hjt4444-10164323-4744302542869887557.doc.pdf-第1页.png

第1页 / 共52页

hjt4444-10164323-4744302542869887557.doc.pdf-第2页.png

第2页 / 共52页

hjt4444-10164323-4744302542869887557.doc.pdf-第3页.png

第3页 / 共52页

hjt4444-10164323-4744302542869887557.doc.pdf-第4页.png

第4页 / 共52页

hjt4444-10164323-4744302542869887557.doc.pdf-第5页.png

第5页 / 共52页

hjt4444-10164323-4744302542869887557.doc.pdf-第6页.png

第6页 / 共52页

hjt4444-10164323-4744302542869887557.doc.pdf-第7页.png

第7页 / 共52页

hjt4444-10164323-4744302542869887557.doc.pdf-第8页.png

第8页 / 共52页

普通本科课程教案（计算机图形学）计算机科学与技术系编印

计算机图形学教案学时：64，其中讲授 52 学时，上机 12 学时。适用专业：计算机科学与技术专业。先修课程：高等数学、线性代数、数据结构、VC++或者ＪＡＶＡ等撰写人：何静涛一、课程的性质、教育目标及任务：计算机图形学是一门研究图形学与图像处理的基本理论、方法及其在智能化检测中应用的学科，是计算机科学与技术等电子信息类本科专业的专业课。本课程侧重于对图形学的基本图元的基本生成，以及图像处理中对图像在空间域与频率域的基本处理算法的研究。并对图形学与图像处理基本理论和实际应用进行系统介绍。目的是使学生系统掌握图形学与图像处理的基本概念、原理和实现方法，学习图形学与图像处理分析的基本理论、典型方法和实用技术，具备解决智能化检测与控制中应用问题的初步能力，为在计算机视觉、模式识别等领域从事研究与开发打下扎实的基础。二、教学内容基本要求： 1．了解图形学与图像处理的发展、应用以及当前国际国内研究的热点和重要成果； 2．理解图形学与图像处理对图元以及图像的分析与理解的以及二维与三维形状重建等； 3．掌握图形学与图像处理中最基本、最广泛应用的概念、原理、理论和算法以及基本技术和方法； 4．能够运用一门高级语言编写简单的图形学与图像处理软件，实现各种图形学与图像处理的算法。三、主要教学内容：学习图形学的基本概念，了解光栅显示系统的原理；掌握基本图元的生成算法：直线的生成算法、曲线的生成算法、多边形的生成算法；掌握区域填充、线段剪裁以及多边形的剪裁；掌握图元的几何变换、以及投影的基本理论。了解图像的概念；图像数字化的基本原理：取样、量化、数字图像的表示；线性系统理论在图像变换，滤波中的应用：线性系统理论、离散图像变换、小波变换；图像编码压缩、增强，以及复原的基本方法：无失真压缩、有失真压缩、变换编码、压缩标准、图像滤波原理、复原滤波器、直方图运算、点运算；图像识别的基本原理和方法：图像分割、图像分析、图像分类．四、参考书目： (1), Baker Donald Hearn & M,Pauline 1

（2),< Computer Graphics with OpenGL, Third Edition> (3),计算机图形学实用技术 (4),计算机图形学 (5) <>, Rafael C. Gonzalez & Richard E. Woods. 陈元琰,张晓竞,科学出版社北京大学出版社 Donald Hearn & M,Pauline Baker 倪明田,吴良芝 Publishing House of Electronics Industry. (6) << Image Processing ,Analysis, and Machine Vision ( second Edition)>> ,Milan Sonka, Vaclav Hlavac. Publishing House of People Post 第一讲图形学基本概念重点：了解图形学概念；掌握图形学中的几个概念：分辨率，光栅，扫描线，像素，帧缓冲器；了解图形学的基本用途；掌握图形学光栅扫描显示系统的工作原理；难点：光栅扫描显示系统的工作原理；教学方法：课堂讨论式教学方法，基于问题式以及启发式教学方法相结合。双语教学。主要内容： 1，什么是计算机图形学？ 2，计算机图形学的主要用途是什么？ 3，计算机图形学中的一些基本概念：什么是分辨率？什么是光栅？什么是光栅扫描系统的扫描线？什么是像素？什么是帧缓冲器？什么是刷新率？图 1.1 扫描线图 1.2 像素点 2

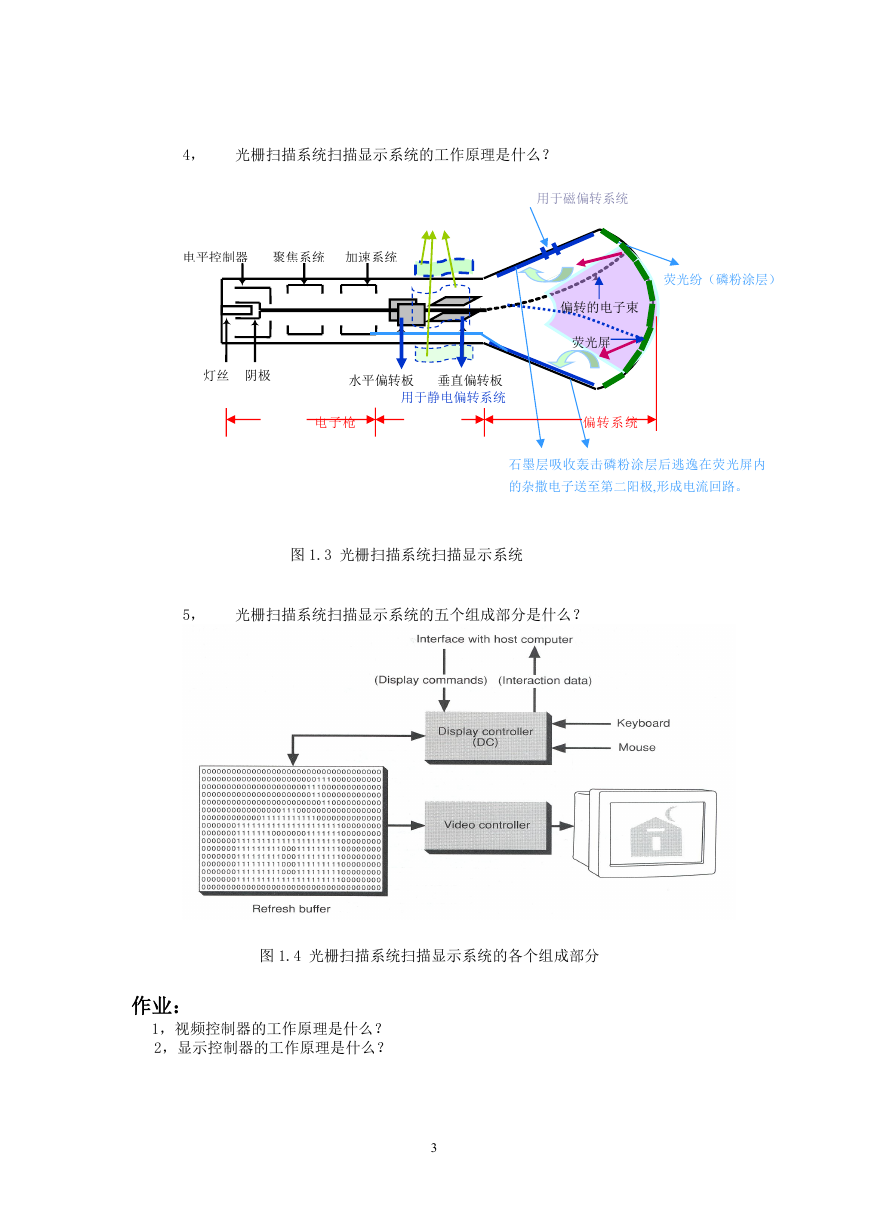
4，光栅扫描系统扫描显示系统的工作原理是什么？电平控制器聚焦系统加速系统用于磁偏转系统偏转的电子束荧光屏荧光纷（磷粉涂层）灯丝阴极水平偏转板垂直偏转板用于静电偏转系统电子枪偏转系统石墨层吸收轰击磷粉涂层后逃逸在荧光屏内的杂撒电子送至第二阳极,形成电流回路。图 1.3 光栅扫描系统扫描显示系统 5，光栅扫描系统扫描显示系统的五个组成部分是什么？图 1.4 光栅扫描系统扫描显示系统的各个组成部分作业： 1，视频控制器的工作原理是什么？ 2，显示控制器的工作原理是什么？ 3

重点：第二讲直线段的生成算法掌握图形学中直线段的几个画法，（1）DDA 算法；（2）中点画线算法；（3）Bresenham 画线算法；难点：对这三个画线算法的理解与实现；教学方法：课堂讨论式教学方法，基于问题式以及启发式教学方法相结合。双语教学。主要内容： 1. 概念扫描变换：确定最佳逼近图形的象素集，并用指定属性写象素； 2. 直线段的扫描转换算法数值微分法(DDA)；中点法；Bresenham 法 (1) DDA 法已知直线段 L(P0, P1), P0 (x0, y0), P1(x1, y1)；直线斜率 k  y x 1 1   y x 0 0 画线过程：从 x 的左端点 x0 开始，向 x 右端点步进，步长=1(个象素)，计算相应的 y 坐 y=Kx+B；取象素点(x, round(y))作为当前点的坐标。计算 yi+1 = kxi+1+B = k1 xi+B+kx = yi+kx 当x =1; 即：当 x 每递增 1，y 递增 k； yi+1 = yi+k 3 Line: P0(0, 0) P1(5, 2) 2 1 DDALine(x0, y0, x1, y1, color) 0 1 2 3 4 5 dx=5, dy=2, k=0.4 0 2 4 x 1 3 5 int(y) y+0.5 0 1 2 0 1 2 0 0.4+0.5 0.8+0.5 1.2+0.5 1.6+0.5 2.0+0.5 6  int x0, y0, x1, y1, color； int x； float dx, dy, y, k; dx, = x1-x0, dy=y1-y0; k=dy/dx, y=y0; for (x=x0; xx1, x++)  drawpixel (x, int(y+0.5), color); y=y+k;   问题 1：当 dx=0，或 dy=0 时过程应怎样处理？问题 2：当 k 1 时过程又应如何处理？ 4

(2) 中点法 ① 基本原理：画直线段的过程中，当前象素点为(xp, yp)，下一个象素点有两种可选择点 p1(xp+1, yp)或 p2(xp+1, yp+1)，若 M=(xp+1, yp+0.5)，即为 p1 与 p2 之中点，且 Q 为理想直线与 x=xp+1 垂线的交点。当 M 在 Q 的下方，则 P2 应为下一点；M 在 Q 的上方，应取 P1 为下一点。 P2 Q P1 M P(xp,yp) ② 算法过程分析：令直线段 L(p0(x0,y0), p1(x1, y1)), 其方程式 F(x, y)=ax+by+c=0 a=y0-y1, b=x1-x0, c=x0y1-x1y0; 点与 L 的关系：on: F(x,y)=0; Up: F(x, y)>0; down: F(x, y)<0; 令 d=F(M)=F(xp+1, yp+0.5)=a(xp+1)+b(yp+0.5)+c 当 d<0，M 在 L(Q 点)下方，取 P2 为下一个象素；当 d>0，M 在 L(Q 点)上方，取 P1 为下一个象素；当 d=0，选 P1 或 P2 均可，约定取 P1 为下一个象素；节省计算的中点增量法， · 若当前象素处于 d0 情况，其位置 d=a(xp+1)+b(yp+0.5)+c 即取 P1 象素要判下一个象素位置，应计算 d1=F(xp+2, yp+0.5)=a(xp+2)+b(yp+0.5)=d+a; · 若 d<0 时，当前象素位置 d=a(xp+1)+b(yp+1.5)+c=d+b 判下一个象素的选择， d2=a(xp+2)+b(yp+1.5)+c=d+a+b 画线从(x0, y0)开始，d 的初值 d0=F(x0+1, y0+0.5)=F(x0, y0)+a+0.5b 因 F(x0, y0)=0，则 d0=a+0.5b，免乘法，d=2a+b(d1, d2 也乘以 2) ③ 算法程序 Midpoint Line (x0, y0, x1, y1, color) int x0, y0, x1, y1, color; { int a, b, d1, d2, d, x, y; a=y0-y1, b=x1-x0, d=2a+b; d1=2a, d2=2(a+b); x=x0, y=y0, drawpixel(x, y, color); while (x

④ 举例 P0(0, 0), P1(5, 2) i 1 2 3 4 5 6 xi 0 1 2 3 4 5 yi 0 0 1 1 2 2 d 1 -3 3 -1 5 1 3 2 1 0 1 2 3 4 问题 1：若上述算法往下取二步(i=2)，则算法和象素的取法将变成怎样？ (3) Bresenham 算法 ① 算法原理类似于中点法，由误差项符号决定下一个象素取右边点还是右上点。算法原理如下: 6 5 0 dy  dx  1  设 y i m , 由 Euler 公式,有: ( xmy i   x i )  my i  i 1  这里, y  i ( i xf ) 。假设在 ix 列已取 ( , i yx ,ri ) ，在 1ix 列真正交点为 ( x i 1  , y i  ! ) ，象素点 ( x i 1  , y i ,1  r ) 应取那个网格点？考虑误差项 ( x ) y   1 i  y , ri i 1   5.0 ，如图， y i ,1  r  ,1 y , ri y , ri     , i ( x  ( x  ) 1  )   0 0 i 1  事实上，我们有如下的递推公式， (  x i  2 )  y i  2  y i ,1  r  5.0  ( x   i  ( x   1  i 1  ) ) ,1   m m  , ( x  ( x  i ) 1  ) 1  i   0 0 且有初值 ( x 2 )  y 2  y 1  5.0  m  5.0 ，于是有如下算法： Bresenhamline (x0, y0, x1, y1, color) int x0, y0, x1, y1, color; { int x, y, dx, dy; float k, e; dx = x1-x0, dy = y1- y0, k=dy/dx; e=-0.5, x=x0, y=y0; for (i=0; idx; i++) {drawpixel (x, y, color); x=x+1，e=e+k; if (e0) 6

{ y++, e--;} } } P0(0, 0), P1(5, 2) x 0 1 2 3 4 5 y 0 0 1 1 2 2 e 0.5 -0.1 -0.7 -0.3 -0.9 -0.5 3 2 1 1 0 Bresenhamline 算法 2 3 4 5 3 2 1 0 1 2 整数 Bresenhamline 算法 3 4 5 InterBresenhamline (x0, y0, x1, y1, color) { P0(0, 0), P1(5, 2) x y e 0 1 0 0 -5 -1 2 1 -7 1 2 2 3 4 5 -3 -9 -5 dx = x1-x0, dy = y1- y0, e=-dx; x=x0, y=y0; for (i=0; idx; -e+) {drawpixel (x, y, color); x++, e=e+2*dy; if (e0) { y++, e=e-2*dx;} } } 作业：推导这三种算法中当直线斜率分别是大于 1 与小于-1 的情况第三讲圆的生成算法重点：掌握图形学中元的生成画法：中点画圆算法；难点：中点画圆算法理解与实现；教学方法：课堂讨论式教学方法，基于问题式以及启发式教学方法相结合。双语教学。主要内容： 1，圆的特征圆被定义为到给定中心位置（xc,yc）距离为r的点集。圆心位于原点的圆有四条对称轴 x=0,y=0,x=y和x=-y。若已知圆弧上一点（x,y）,可以得到其关于四条对称轴的其它7个点，这种性质称为八对称性。因此，只要扫 7

资料库

《计算机图形学》教案.doc

相关推荐

课程资源

热门标签

最新资料