10.1109/ULTSYM.2011.0481 1-3 Microfabricated Composite Acoustic Matching Layers for High Frequency Transducers Tung Manh, Lars Hoff Institute of Micro and Nano Systems Technology Vestfold University College Horten, Norway Tung.Manh@hive.no Tonni Franke Johansen Department of Circulation and Medical Imaging Norwegian University of Science and Technology Trondheim, Norway Geir Uri Jensen Department of Microsystems and Nanotechnology SINTEF ICT Oslo, Norway the paper presents fabrication and Abstract—This characterization of a 1-3 silicon-polymer composite matching layer made by Deep Reactive Ion Etch (DRIE) method. A well- defined composite layer thickness of 83 µm was obtained by using Silicon-on-Insulator (SOI) wafers as substrate. The resulting composite has 7 µm size posts and 9 µm spacing between posts. A slight tapering of the posts was observed after the DRIE process, causing the posts to be narrower in the bottom than at the top. The composite was used as acoustic matching layer in an air- backed 15 MHz transducer and characterized by electrical impedance measurements in air. The effective acoustic properties of the composite, speed of sound and acoustic impedance, deduced from measured results, were found to be lower than those predicted from iso-strain model. This deviation can be explained by tapering of the trench walls and the dispersion caused by the finite dimensions of the bi-phase material, an explanation that was verified by FEM simulations. Keywords-1-3 composite; acoustic matching layers; silicon micromachining; high frequency transducers. I. INTRODUCTION for high frequency High frequency broadband ultrasound transducers provide high resolution images in situations where the imaging depth is small, e.g. in intravascular ultrasound. In such transducers, one or more acoustic matching layers are used to effectively couple energy from the transducer to the tissue. We have previously presented methods to fabricate such matching layers using micromachining technologies from Micro-Electro-Mechanical Systems (MEMS) industry, such as photolithography and etch [1]. The acoustic matching is a silicon-polymer composite, of 2-2 or 1-3 connectivity, where the silicon substrate is micromachined and filled with epoxy resin. Different micromachining methods can be used to fabricate such a layer, e.g. anisotropic wet etch of <110>-oriented silicon wafer or Deep Reactive Ion Etch (DRIE) by the Bosch- process. Anisotropic wet etch depends on the crystal orientation, and is only suitable to form 2-2 composite transducers layer by structures. This method requires a very good alignment of the feature lines along the <111> crystal planes, which can be demanding at the small dimensions needed for transducers working at high frequencies. This paper describes fabrication of 1-3 composites by DRIE method. This technology is not sensitive to crystal orientation, and is promising for mass production. The process uses a Silicon-on-Insulator (SOI) wafer with a buried silicon dioxide layer to stop the etching at a well-defined thickness, 83 µm. The composite fabricated by this method was bonded to a 15MHz PZT disc with coaxial electrodes, forming an air- backed ultrasound transducer. Composite properties were calculated from electrical measurements in air, and compared to values calculated from the iso-strain model. II. THEORY A. The iso-strain model A composite behaves acoustically like a homogeneous material if its lateral dimensions are sufficiently fine. Within this regime, effective elastic parameters of the composite can be calculated from the theoretical model developed by Smith et al. [2] without piezoelectric coupling. The resulting effective parameters for a 1-3 composite are = C c 33 ⎡ ⎢ ⎢ v c ⎢ ⎢ ⎢ ⎣ Si 11 2 + p ⎛ c ⎜ 12 ⎝ Si ⎞ c ⎟ 12 ⎠ − ˆ v Si c 11 ˆ v ⎛ ⎜ ⎝ 2 − Si ⎞ c ⎟ 12 ⎠ p + ν ⎛ c ⎜ 11 ⎝ = v Z Si ˆ p C ρ ρ ρ + % v C C C c ρ 33 C c 33 C ρ V C = = ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ + p c 12 ⎞ ⎟ ⎠ + ˆ vc p 11 (1) (2) (3) (4) This work is funded by the Research Council of Norway under Grants No. 176540, 191282, and 181712/I30. 978-1-4577-1252-4/11/$26.00 ©2011 IEEE 1932 2011 IEEE International Ultrasonics Symposium Proceedings 

etched structures vacuum filled by epoxy resin (Spurrs, Electron Microscopy Sciences, PA, USA) to form the composite material. The impregnated wafers were cured at 70°C for 8 hours. The composite with high aspect ratio posts in polymer matrix is shown in Fig. 1. The processed wafers were diced into 6mm x 6mm dies using a Disco Abrasive Systems dicing saw (Disco Corporation, Japan). The top polymer and bottom silicon layers of each sample were grinded and polished, leaving only the composite layer. This lapping process was done using MultiPrepTM System grinding and polishing equipment (Allied High Tech Products Inc, USA) with a coarse to fine grit scheme. The final lapping particle diameter was 5 µm and the polishing chemical was a mixture of colloidal silica and 0.05 µm alumina (Allied High Tech Products Inc, USA). Figure 2. The real and imaginary parts of the electrical impedance of an air backed transducer simulated in FEM, using a silicon-polymer composite as acoustic matching layer on top of the piezoelectric plate with different composite unit sizes. The solid curve with no symbols (-) corresponds to an effective composite material using the iso-strain model. The dotted curve (·) is p), solid curve with circles with a kerf of 1/16 shear wavelength in polymer (λs p, solid curve with arrows (-〈-) is with a kerf of 1/2 (-o-) is with a kerf of 1/8 λs p. λs Figure 1. SEM image of the 1-3 composite with silicon posts (light color) in polymer matrix (dark color). where the overbars ( x ) refer to effective parameters of the composite, superscript p refer to parameters of the polymer, superscript Si to parameters of the silicon substrate, and ijc are the elastic superscript C to parameters of the composite. coefficients of the materials, ρis the density; v is the volume fraction of silicon in the composite, with being the CZ is the effective acoustic volume fraction of polymer. CV is the longitudinal wave speed of the impedance and composite, both measured in the thickness direction. B. Finite Element Method (FEM) model −= 1ˆ v v The iso-strain model is widely used due to its simplicity. However, as it is a 1D model, it can only capture the thickness vibration mode, and it will also ignore the finite dimensions of the composite structure. Moreover, deviations from a perfect structure, such as the tapering profile of the walls from the DRIE process, cannot be described by a simple 1D model. To investigate these effects, a 3D finite element method (FEM) model of the transducer was set up using COMSOL Multiphysics, version 4.1 (Comsol AB, Stockholm, Sweden), The FEM model was made for a transducer with center frequency 15 MHz, consisting of one composite silicon- polymer layer for acoustic matching and a PZT plate as the active element. Several different composite dimensions were tested, while keeping the silicon volume fraction constant at 0.19. The composite period was increased in steps of kerf sλ being the shear wavelength in polymer. size sλ , with p p /16 III. FABRICATION AND CHARACTERIZATION MATERIAL PROPERTIES FOR 1-3 COMPOSITE MATCHING LAYER TABLE I A. Fabrication First, a 0.5 μm aluminum layer was sputtered on top of the SOI wafer. The Al layer was patterned by 1.5 μm photoresist, etched to create a mask for the DRIE process, and the photoresist removed by plasma stripping. DRIE was done in an AMS 200 I-Productivity machine (Alcatel Micro Machining Systems, Annecy, France) using an LF (Low Frequency) bias process. The Al mask and polymer were stripped in piranha solution. The wafer was rinsed in DI water, air dried, and the Parameter Density (kg/m3) Thickness (µm) Longitudinal wave velocity (m/s) Acoustic impedance (MRayl) Mechanical loss factor Dimension Measured at Fitted Top 1335 83 4730 6.32 ― Bottom 1278 83 4336 5.54 ― 1309 83 4126 5.40 27.1 1933 2011 IEEE International Ultrasonics Symposium Proceedings 

were used to find the material coefficients of the PZT in thickness mode. Then, the composite layers were bonded to the PZT discs, and impedance measurements on this structure were used to extract the properties of the silicon-polymer composite. All impedance measurements were done in air, using an HP 8753D Network Analyzer (Agilent Technologies, Santa Clara, CA, USA), with the PZT discs connected to the SMA connector. Before bonding to the piezoelectric disc, feature sizes from the top and bottom of the composite were measured under microscope, and initial estimates for the material parameters were calculated using the iso-strain model. Improved values three composite material parameters, acoustic for CZ , longitudinal wave speed CV , and Q-factor impedance CQ , were found by fitting the measured electrical impedance curves to calculations from the Mason model, using the iso- strain estimates as start values. The fitting was done using a non-linear regression scheme, the Nelder-Mead simplex method, implemented in MATLAB (The Mathworks Inc., Natick, MA, USA). The thickness of the composite layers is accurately defined by the device layer thickness in the SOI wafer, and the PZT material parameters were known from electrical impedance measurements on the PZT disc alone. the Figure 3. Real and imaginary parts of electrical impedances of the transducer simulated in FEM. Solid line with circles (-o-) is the electrical impedance without tapering effect and post width of 6.1 µm. Dotted line (·) is the electrical impedance with linear tapering, post width of 7.0 µm at the top and 0.3° angle profile. Solid line (-) is the electrical impedance without tapering effect and post width of 7.0 µm. To form an ultrasound transducer, the composite was glued to a 5mm diameter coaxial piezoelectric disc (PZT5A, Boston Piezo-optics, Bellingham, MA), using Spurrs epoxy as adhesion. The diameter of the center electrode of the coaxial disc is 3.2 mm, the gap between the center electrode and the outer ring is 0.4 mm, and the outer ring has width 0.4 mm. The coaxial electrodes allow electrical connection to both electrodes from the back side of the transducer. The transducer was mounted on an SMA electrical connector, connecting the outer wrapping electrode of the disc to the outer ground part of the connector. The center electrode of the disc was electrically connected to the center of the SMA connector via a thin wire, using conductive epoxy as adhesion (Epo-Tek EE129-4, Epoxy Technology, Inc., Bellerica, MA). This creates an air- backed transducer consisting of a piezo-electric plate and one silicon-polymer composite acoustic matching layer. A Teflon tube was designed to cover the SMA as housing, making it waterproof. B. Characterization Acoustic properties of the composite layer were estimated from electrical impedance measurements on the transducer. This was done in a two-step approach. First, electrical impedance measured on the piezoelectric coaxial discs alone (a) (b) Figure 4. 1-3 composite structure of the layer used to make air-backed transducer in this paper (a) top view and (b) bottom view. The images show the reduction of silicon volume fraction at the bottom compared to that on the top. The post sizes are 7.0µm at the top and reduced to 6.1µm in the bottom. 1934 2011 IEEE International Ultrasonics Symposium Proceedings 

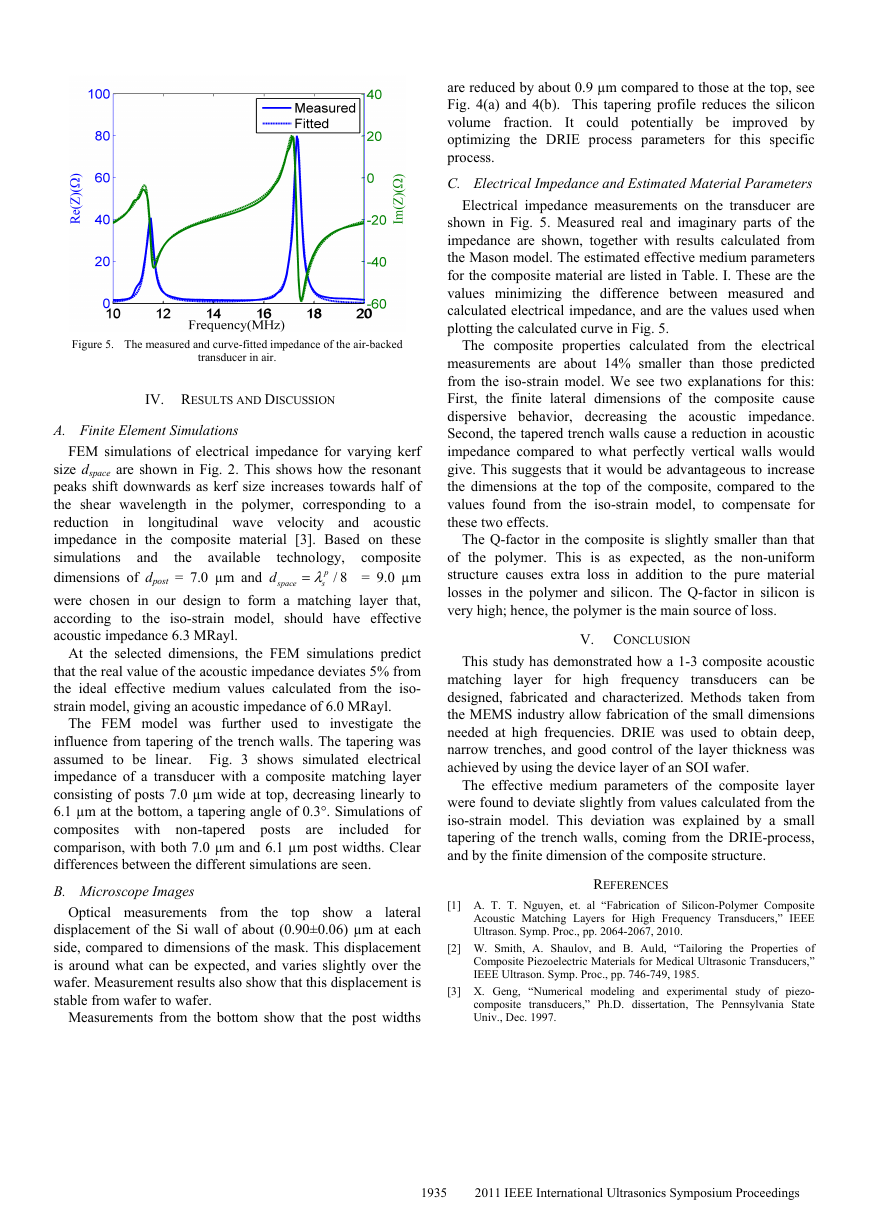
are reduced by about 0.9 µm compared to those at the top, see Fig. 4(a) and 4(b). This tapering profile reduces the silicon volume fraction. It could potentially be improved by optimizing the DRIE process parameters for this specific process. C. Electrical Impedance and Estimated Material Parameters Electrical impedance measurements on the transducer are shown in Fig. 5. Measured real and imaginary parts of the impedance are shown, together with results calculated from the Mason model. The estimated effective medium parameters for the composite material are listed in Table. I. These are the values minimizing the difference between measured and calculated electrical impedance, and are the values used when plotting the calculated curve in Fig. 5. The composite properties calculated from the electrical measurements are about 14% smaller than those predicted from the iso-strain model. We see two explanations for this: First, the finite lateral dimensions of the composite cause dispersive behavior, decreasing impedance. Second, the tapered trench walls cause a reduction in acoustic impedance compared to what perfectly vertical walls would give. This suggests that it would be advantageous to increase the dimensions at the top of the composite, compared to the values found from the iso-strain model, to compensate for these two effects. the acoustic The Q-factor in the composite is slightly smaller than that of the polymer. This is as expected, as the non-uniform structure causes extra loss in addition to the pure material losses in the polymer and silicon. The Q-factor in silicon is very high; hence, the polymer is the main source of loss. V. CONCLUSION layer for high frequency This study has demonstrated how a 1-3 composite acoustic matching transducers can be designed, fabricated and characterized. Methods taken from the MEMS industry allow fabrication of the small dimensions needed at high frequencies. DRIE was used to obtain deep, narrow trenches, and good control of the layer thickness was achieved by using the device layer of an SOI wafer. The effective medium parameters of the composite layer were found to deviate slightly from values calculated from the iso-strain model. This deviation was explained by a small tapering of the trench walls, coming from the DRIE-process, and by the finite dimension of the composite structure. REFERENCES [1] A. T. T. Nguyen, et. al “Fabrication of Silicon-Polymer Composite Acoustic Matching Layers for High Frequency Transducers,” IEEE Ultrason. Symp. Proc., pp. 2064-2067, 2010. [2] W. Smith, A. Shaulov, and B. Auld, “Tailoring the Properties of Composite Piezoelectric Materials for Medical Ultrasonic Transducers,” IEEE Ultrason. Symp. Proc., pp. 746-749, 1985. [3] X. Geng, “Numerical modeling and experimental study of piezo- composite transducers,” Ph.D. dissertation, The Pennsylvania State Univ., Dec. 1997. Figure 5. The measured and curve-fitted impedance of the air-backed transducer in air. IV. RESULTS AND DISCUSSION A. Finite Element Simulations d space in FEM simulations of electrical impedance for varying kerf size dspace are shown in Fig. 2. This shows how the resonant peaks shift downwards as kerf size increases towards half of the shear wavelength in the polymer, corresponding to a reduction longitudinal wave velocity and acoustic impedance in the composite material [3]. Based on these simulations and technology, composite the available dimensions of dpost = 7.0 µm and = 9.0 µm were chosen in our design to form a matching layer that, according to the iso-strain model, should have effective acoustic impedance 6.3 MRayl. λ= / 8p s At the selected dimensions, the FEM simulations predict that the real value of the acoustic impedance deviates 5% from the ideal effective medium values calculated from the iso- strain model, giving an acoustic impedance of 6.0 MRayl. The FEM model was further used to investigate the influence from tapering of the trench walls. The tapering was assumed to be linear. Fig. 3 shows simulated electrical impedance of a transducer with a composite matching layer consisting of posts 7.0 µm wide at top, decreasing linearly to 6.1 µm at the bottom, a tapering angle of 0.3°. Simulations of composites with non-tapered posts are for comparison, with both 7.0 µm and 6.1 µm post widths. Clear differences between the different simulations are seen. B. Microscope Images included the top show a Optical measurements from lateral displacement of the Si wall of about (0.90±0.06) µm at each side, compared to dimensions of the mask. This displacement is around what can be expected, and varies slightly over the wafer. Measurement results also show that this displacement is stable from wafer to wafer. Measurements from the bottom show that the post widths 1935 2011 IEEE International Ultrasonics Symposium Proceedings