logo资料库

基于组合权重的灰色关联理想解法及其在教师素质评价中的应用.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.18M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    http://www.paper.edu.cn 基于组合权重的灰色关联理想解法及其在教师素质 评价中的应用 杜成喜，张玥 北京市房山区教育委员会，北京 （102488） E-mail：zhangyue.bit@163.com 摘 要：引入灰色系统理论，对传统理想解法（TOPSIS）进行了拓展，提出了一种基于组 合权重的灰色关联理想解法（GC-TOPSIS）。利用 AHP 和熵值法对决策指标进行组合赋权， 依据灰色关联分析理论，以灰色关联度为决策单元构造 GC-TOPSIS 模型，最后通过一个教 师素质评价的实例验证了方法的有效性和可行性。 关键词：层次分析法；熵值法；传统理想解法；灰色关联度；灰色关联理想解法 中图分类号：G4 1．引言 理想解法（Technique for Order Preference by Similarity to Ideal Solution，TOPSIS）由 Hwang 和 Yoon 于 1981 年提出，直译为逼近理想解的排序方法，是一种有效的多指标决策 方法。其基本思路是通过构造多指标问题的理想解和负理想解，并以靠近理想解和远离负理 想解两个基准作为评价各对象的判断依据，因此理想解法又称为双基准法。理想解法基于确 定性数据样本，分析的依据是数据序列之间确定的距离关系。然而，在多指标决策过程中往 往是统计数据非常有限，加上人为的因素，许多数据波动较大，没有典型的分布规律，而且 既有定性因素，又有定量因素，因素之间不都具有确定的数量关系，也就是部分信息已知， 部分信息未知，是一种典型的灰色系统。在“贫信息”情况下，传统数学方法在客观、全面地 分析此类问题时就显得无能为力了。而具有所需原始数据少、原理简单、运算方便、易于挖 掘数据规律等优点的灰色系统理论，尤其是灰色关联分析理论在处理此类问题时能取得令人 满意的结果。 另外，传统理想解法在确定决策指标的权重系数时，或者用客观赋权法[1，2]，或者用主 观赋权法[3]，只有少数文献[4]考虑到了二者的结合。然而事实上，在分析的初始阶段，由于 样本数据较少，数据间的内在规律还没有形成，应注重专家的经验估计，以主观赋权为主； 随着样本数据的不断积累，可以利用指标间的内在规律来确定指标的权重系数，此时应以客 观赋权为主。因此，合理的赋权方法应该同时基于指标数据之间的内在规律和专家经验对决 策指标进行赋权[5，6]。为此，本文引入灰色系统理论对传统的理想解法进行拓展，提出了一 种 基 于 组 合 赋 权 思 想 和 考 虑 决 策 者 偏 好 程 度 的 灰 色 关 联 理 想 解 法 （Grey Correlation Technique for Order Preference by Similarity to Ideal Solution，GC-TOPSIS），为“贫信息”环 境下的多指标决策问题提出了一种新思路。 2．指标权重的确定 理想解法的前提是对决策指标进行赋权。权重的确定方法主要有两种：一是主观赋权法， 即指标权重由专家根据经验主观判断而得到，决策结果具有较强的主观随意性，如层次分析 法（AHP）、最小平方法、专家调查法（Delphi 法）、环比评分法、TAC-TIC 法等，其中 AHP 应用广泛，能将复杂问题层次化，将定性问题定量化，是一种较合理的主观赋权方法； 二是客观赋权法，即根据原始数据之间的关系来确定权重，具有较强的数学理论依据，如主 - 1 -
    http://www.paper.edu.cn 成分分析法、熵值法、离差及均方差法等。其中熵值法应用较多，它依据指标所包含的信息 量的大小确定指标权重。为了使决策结果更真实、可靠、更符合客观实际，针对主、客观赋 权法的优缺点，本文在确定 GC-TOPSIS 指标权重时运用博弈论方法将主观权重和客观权重 融合起来，得到一个均衡的综合权重。 （1）基于博弈论的综合权重法[7] 为了提高多属性权重赋值的科学性，可使用 L 种方法对指标进行赋权，由此构造一个 ，将这 L 个向量任意线性组合就构成了一个可能 W { ωω 2 , 1 }l ω = , , K 基本的权重集 的权重集 W l = ∑ k 1 = αωα k k T k ( > )0 （1） 的 ∗ kω ，本文采用了博弈论的方法来获得 ∗ ω视为可能的权重集的一种可能的权重向量。如何在可能的权重向量集中找到最满意 kω 。它的基本思想是在不同的权重之间寻找一致或 妥协，即极小化可能的权重跟各个基本权重之间的各自偏差。因此，寻找最满意的权向量， 可归结为对式（1）中 L 个线性组合系数 kα 进行优化，优化的目标是使ω与各个 kω 的离差 的极小化。如此，导出了下面的对策模型： min l ∑ j 1 = ωωα i − j T j i ( = ,2,1 , K L ) （2） 2 由矩阵的微分性质可以得出式（2）的最优化一阶导数条件，即为如下矩阵： 1 T ⎡ ωω 1 ⎢ ⎢ ⎢ T ωω ⎣ 1 M l K K T ωω l 1 M T ωω l l ⎤ ⎥ ⎥ ⎥ ⎦ α ⎛ 1 ⎜ α ⎜ 2 ⎜ ⎜⎜ ⎝ K α l ⎞ ⎟ ⎟ ⎟ ⎟⎟ ⎠ = 1 2 T ⎡ ωω 1 ⎢ T ωω ⎢ 2 ⎢ K ⎢ T ωω ⎢ ⎣ l l （3） ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 计算求得( αα 2 1 , , , K )lα ，然后再对其进行归一化处理。即 因此，综合权重为 / ααα k ∗ = k k l ∑ k 1 = （4） l ∗ ω ∑ 1 = （2）熵值法和层次分析法确定权重 分别采用一种主观赋权法（层次分析法）和一种客观赋权法（熵值法）来组成可能的权 （5） T ωα k = • ∗ k k 重集，运用博弈论方法将两者融合、协调，得到最优的权重向量。 3．灰色关联理想解法（GC-TOPSIS） 灰色关联分析[8，9]的基本思想是对系统数据序列几何关系和曲线几何形状的相似程度进 行比较分析，以曲线间相似程度大小作为关联程度的衡量尺度。曲线越接近，相应序列之间 的关联度越大，反之则越小。因此对于多指标决策问题来说，如果某一方案与系统设置的虚 拟理想方案的关联度越大，就可以认为该方案越接近理想方案。因此本文提出了一种基于灰 色关联分析的灰色关联理想解法（GC-TOPSIS）。基本思路是：首先按照传统 TOPSIS 法确 - 2 -
    定理想方案和负理想方案，然后利用灰色关联理论采用灰色关联度去测评各方案指标数列与 理想方案和负理想方案的关联程度，最后按照方案的灰色关联相对贴近度对方案进行优劣排 序。具体步骤如下： http://www.paper.edu.cn （1）设有 m 个方案，n 个指标，指标值为 nmijx ( ) × = 。用向量归一化法对决策矩阵作标准化处理，得标准化矩阵 xij 1( ≤≤ mi 1, ≤≤ j n ) Y ，则决策矩阵 = ( nmijy ) × ，其 X 中 y ij = ij x m ∑ i 1 = i ( = ,2,1 , K jm ; = ,2,1 , K n ) x 2 ij （2）计算加权标准化矩阵 U = u ( ) nmij × = ( ∗ ω j y ) nmij × = m （3）确定理想方案和负理想方案 理想方案： U + 0 ju )(max {( imi 1 ≤≤ ju )(min (, imj 1 ≤≤ ∈ = J j j + 1 2 U ⎡ ⎢ U ⎢ ⎢ M ⎢ U ⎣ = ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ u 1 u 2 ⎡ ⎢ ⎢ ⎢ ⎢ u ⎣ )1( )1( u 1 u 2 )2( )2( nu )( 1 nu )( 2 K K M )1( m MKM nu )2( )( m K u m ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ ∈ J − ))} = u ( + 0 ),1( u + 0 ),2( , K ju ), ( + 0 , K nu ))( + 0 负理想方案： ju U )(max {( − imi 0 1 ≤≤ = Jj ∈ + ju )(min (, imj 1 ≤≤ Jj ∈ − ))} = u ( − 0 ),1( u − 0 ),2( , K ju ( ), − 0 , K nu ))( − 0 其中 +J 是值越大越好的指标集合， −J 是值越小越好的指标集合。 （4）计算第 i 个方案与理想方案关于第 j 个指标的灰色关联系数 ∈ )1,0( （6） r =+ ij , ζ Mm + ζ M k )( + ζ m min ， = Δ i ku )( i 其中， Δ i k )( = ku )( + 0 − 分辨系数，一般取值 0.5。 min k Δ i k )( ， M = max i max k Δ i k )( ；ζ 为 i 则各方案与理想方案的灰色关联系数矩阵 + R = r + 11 r + 21 M r + m 1 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ r + 12 r + 22 r + n 1 r + n 2 K K MKM r r + + m mn 2 K ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 第 i 个方案与理想方案的灰色关联度为 R + i n 1 = ∑ n 1 = j r + ij i (, = ,2,1 , K m ) （7） 同理，第 i 个方案与负理想方案关于第 j 个指标的灰色关联系数 r =− ij Mm + ζ M k )( + ζ i Δ , ζ ∈ )1,0( （8） - 3 -
    其中， Δ i k )( = ku )( − 0 − ku )( i ， m = min i min k Δ i k )( ， M = max i max k Δ i k )( 。 则各方案与负理想方案的灰色关联系数矩阵 http://www.paper.edu.cn − R = r − 11 r − 21 M r − m 1 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ r − 12 r − 22 r − n 1 r − n 2 K K MKM r r − − m mn 2 K ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ 第 i 个方案与负理想方案的灰色关联度为 R − i n 1 = ∑ n 1 = j r − ij i (, = ,2,1 , K m ) （9） （5）计算每个方案的灰色关联相对贴近度 C i = R + i + R − i R + i i (, = ,2,1 , K m ) （10） 由灰色关联定理[8]可知，系统中任何两个行为序列都不可能严格无关联，即 iR < − 值得指出的是，当某一方案与理想方案的关联度较大时，一般可以认为该方案接近于理 ，这与传统 TOPSIS 的相对贴近度不同。 。因此灰色关联相对贴近度 < iC iR < + ≤ < ≤ 1 1 0 1 0 ， 0 想方案。但为了全面评价方案的优劣，必须同时考虑方案与负理想方案的关联度。然而有时 会出现某一方案同时与理想方案和负理想方案的关联度都较大的情况。因此，本文引入偏好 系数对评价公式进行修正。 C j = ⎧ ⎪ ⎨ ⎪⎩ R + θ i + R R − + + θ θ i i − + R + i 0 < θ + < 0;1 < θθ − = ;1 + θ − 0 = < 1 , i ( = ,2,1 , K m ) （11） 其中， +θ 和 −θ 为偏好系数，它们分别反映了决策者对评价方案与理想方案、评价方案 < +θ ， 与负理想方案关联度的偏好程度或者关心程度。一般取 + >θθ − ，并满足 ≤ 1 0 0 ≤ −θ ， < 1 + − + θθ 1= 。若 + − + θθ 1≠ ，则可进行归一 化处理，令 =′ θ + θ + + θθ − + ， =′ θ − θ − + θθ − + ，此时 1=′+′ + θθ − 。当 = − + θθ = 1 2 时，灰色关联相对贴近度就变为公式（10） 表示的形式了。 （6）根据灰色关联相对贴近度的大小对各方案进行排序。贴近度越大，则方案越优； 反之，贴近度越小，则方案越劣。 4．实证分析 为了进一步说明 GC-TOPSIS 的步骤，本文以教师素质评价问题进行了实证分析。教师 素质的综合评价指标包括责任感、专业水平、工作绩效、品德操行以及工作意愿。各评价指 标的定量化表示以及各参评教师评价指标的原始数据如表 1 所示。 教师 责任感 专 业 水 工 作 绩 品 德 操 工 作 表 1 各参评教师评价指标的原始数据 - 4 -
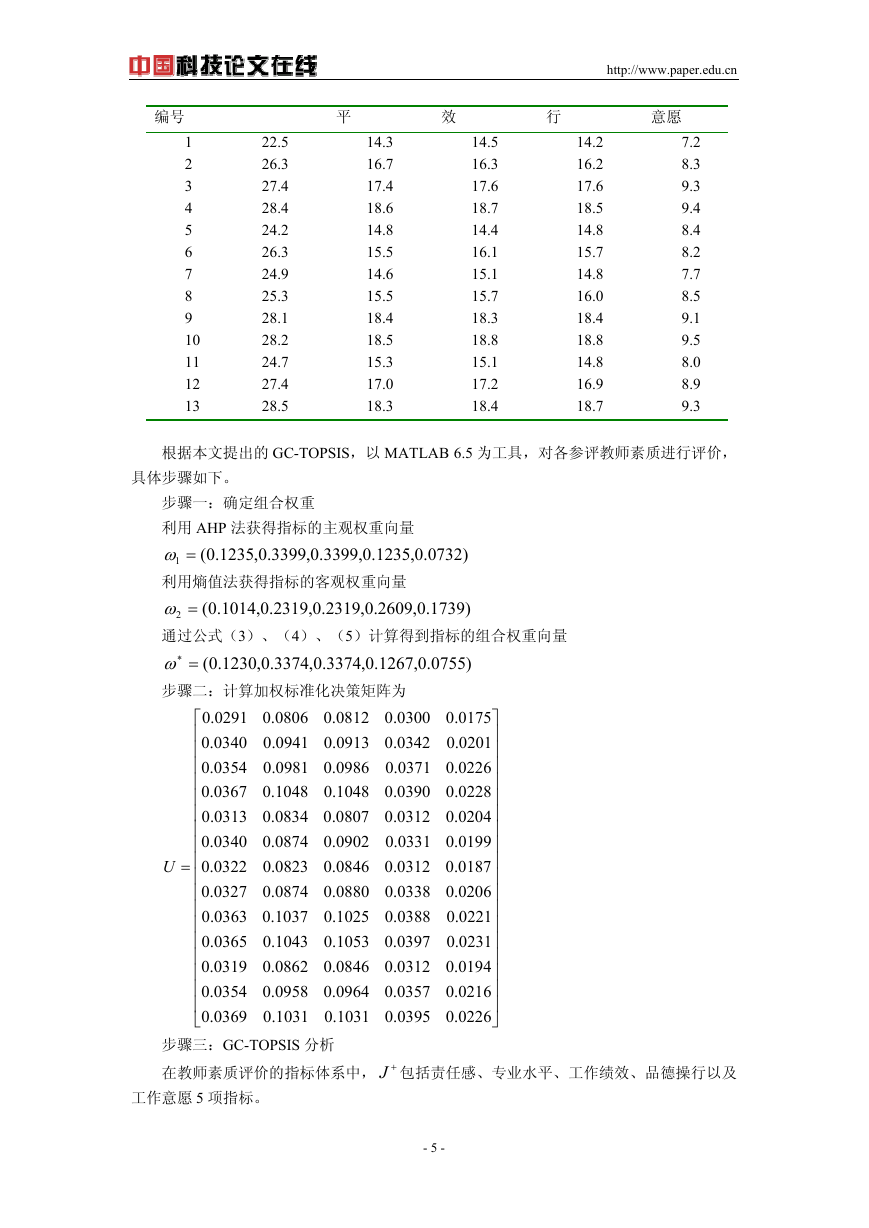
    编号 1 2 3 4 5 6 7 8 9 10 11 12 13 22.5 26.3 27.4 28.4 24.2 26.3 24.9 25.3 28.1 28.2 24.7 27.4 28.5 http://www.paper.edu.cn 平 效 行 意愿 14.3 16.7 17.4 18.6 14.8 15.5 14.6 15.5 18.4 18.5 15.3 17.0 18.3 14.5 16.3 17.6 18.7 14.4 16.1 15.1 15.7 18.3 18.8 15.1 17.2 18.4 14.2 16.2 17.6 18.5 14.8 15.7 14.8 16.0 18.4 18.8 14.8 16.9 18.7 7.2 8.3 9.3 9.4 8.4 8.2 7.7 8.5 9.1 9.5 8.0 8.9 9.3 根据本文提出的 GC-TOPSIS，以 MATLAB 6.5 为工具，对各参评教师素质进行评价， 具体步骤如下。 .0( 3399 .0, 3399 .0, 1235 .0, 步骤一：确定组合权重 利用 AHP 法获得指标的主观权重向量 .0, 1235 1 =ω 利用熵值法获得指标的客观权重向量 2609 2 =ω 通过公式（3）、（4）、（5）计算得到指标的组合权重向量 .0(=∗ω 1267 步骤二：计算加权标准化决策矩阵为 0755 ) 3374 3374 .0, 1230 .0, 2319 .0, 1014 .0, 2319 .0, .0, 1739 0732 ) .0( ) .0, .0, U = 0.0291 0.0340 0.0354 0.0367 0.0313 0.0340 0.0322 0.0327 0.0363 0.0365 0.0319 0.0354 0.0369 ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ 0.0806 0.0941 0.0981 0.1048 0.0834 0.0874 0.0823 0.0874 0.1037 0.1043 0.0862 0.0958 0.1031 0.0812 0.0913 0.0986 0.1048 0.0807 0.0902 0.0846 0.0880 0.1025 0.1053 0.0846 0.0964 0.1031 0.0300 0.0342 0.0371 0.0390 0.0312 0.0331 0.0312 0.0338 0.0388 0.0397 0.0312 0.0357 0.0395 0.0175 ⎤ ⎥ 0.0201 ⎥ 0.0226 ⎥ ⎥ 0.0228 ⎥ ⎥ 0.0204 ⎥ 0.0199 ⎥ ⎥ 0.0187 ⎥ 0.0206 ⎥ ⎥ 0.0221 ⎥ 0.0231 ⎥ ⎥ 0.0194 ⎥ ⎥ 0.0216 ⎥ 0.0226 ⎦ 步骤三：GC-TOPSIS 分析 在教师素质评价的指标体系中， +J 包括责任感、专业水平、工作绩效、品德操行以及 工作意愿 5 项指标。 - 5 -
    http://www.paper.edu.cn 最终确定的理想解和负理想解分别为 0 =+U 0 =−U 按照公式（6）、（8）计算各参评教师与理想解和负理想解的关联系数矩阵分别为 048,0.1053 806,0.0807 0.0369,0.1 0.0291,0.0 ,0.0397,0. ,0.0300,0. 0231 ) ) 0175 ( ( R =+ R =− 0.6119 ⎡ ⎢ 0.8092 ⎢ 0.8913 ⎢ ⎢ 0.9840 ⎢ ⎢ 0.6872 ⎢ 0.8092 ⎢ ⎢ 0.7235 ⎢ 0.7455 ⎢ ⎢ 0.9535 ⎢ 0.9685 ⎢ ⎢ 0.7110 ⎢ ⎢ 0.8913 ⎢ 1.0000 ⎣ 1.0000 ⎡ ⎢ 0.7151 ⎢ 0.6613 ⎢ ⎢ 0.6181 ⎢ ⎢ 0.8483 ⎢ 0.7151 ⎢ ⎢ 0.7987 ⎢ 0.7736 ⎢ ⎢ 0.6308 ⎢ 0.6244 ⎢ ⎢ 0.8146 ⎢ ⎢ 0.6613 ⎢ 0.6119 ⎣ 0.3370 0.5348 0.6474 1.0000 0.3650 0.4141 0.3534 0.4141 0.9179 0.9609 0.3981 0.5775 0.8786 1.0000 0.4767 0.4128 0.3370 0.8146 0.6440 0.8786 0.6440 0.3475 0.3417 0.6872 0.4473 0.3534 0.3379 0.4677 0.6474 0.9609 0.3333 0.4489 0.3727 0.4155 0.8146 1.0000 0.3727 0.5802 0.8483 0.9609 0.5371 0.4073 0.3379 1.0000 0.5642 0.7593 0.6276 0.3607 0.3333 0.7593 0.4393 0.3545 0.5591 0.6910 0.8255 0.9462 0.5913 0.6508 0.5913 0.6758 0.9318 1.0000 0.5913 0.7546 0.9840 1.0000 0.7455 0.6340 0.5775 0.9111 0.7987 0.9111 0.7640 0.5829 0.5591 0.9111 0.6833 0.5642 0.6872 ⎤ ⎥ 0.8039 ⎥ 0.9609 ⎥ ⎥ 0.9762 ⎥ ⎥ 0.8200 ⎥ 0.7935 ⎥ ⎥ 0.7365 ⎥ 0.8311 ⎥ ⎥ 0.9248 ⎥ 1.0000 ⎥ ⎥ 0.7688 ⎥ ⎥ 0.8913 ⎥ 0.9609 ⎦ 1.0000 ⎤ ⎥ 0.8255 ⎥ 0.7069 ⎥ ⎥ 0.6989 ⎥ ⎥ 0.8092 ⎥ 0.8367 ⎥ ⎥ 0.9111 ⎥ 0.7987 ⎥ ⎥ 0.7278 ⎥ 0.6872 ⎥ ⎥ 0.8662 ⎥ ⎥ 0.7500 ⎥ 0.7069 ⎦ 按照公式（7）、（9）计算各参评教师与理想解和负理想解的灰色关联度为 (=+R 613,0.7945 0.5066,0.6 ,0.9735,0. ,0.5139,0. 6.0=+θ 5594,0.623 8766,0.711 4.0=−θ 3,0.5555,0 7,0.8518,0 .6164,0.90 .7216,0.52 85,0.9859, 99,0.5091, 0.5684,0.7 0.8077,0.5 962,0.5182 ) 。按照公式（11）计算得到每个参评教师的 390,0.934 ) ， (=−R 0.9922,0.6 600,0.5645 取决策者的偏好系数 灰色关联相对贴近度 ,0.7397,0. 0.4337,0.6 005,0.6786 4891,0.567 (=C 根据灰色关联相对贴近度的大小对各参评教师进行排序，排序结果为 10 表明 10 号参评教师综合素质评价质量最佳，其次是 4 号参评教师，再其次是 13 号参评 0.5135,0.6 00,0.7439, .5617,0.72 8,0.4945,0 ffff 503,0.730 ) fff fff 15 ff 12 13 2 3 9 4 6 8 11 7 - 6 -
    http://www.paper.edu.cn 教师，最差的是 1 号参评教师。通过对比可以发现本文的排序结果完全和文献[10]中的排序 相一致，这说明 GC-TOPSIS 具有很好的可行性和有效性。 5．结束语 在多指标决策过程中，实际问题往往是一种“部分信息已知、部分信息未知”的典型灰色 系统问题。传统数学方法在对此类问题的处理上有较大的局限性。为此，本文引入灰色系统 理论，并考虑决策者的偏好程度对传统 TOPSIS 进行了拓展，提出了一种灰色关联理想解法 —GC-TOPSIS，以期能为“贫信息”条件下的多指标决策做一点有意义的尝试，并通过一个实 际算例验证了方法的有效性和可行性。作为一种尝试，GC-TOPSIS 难免存在例如决策者的 偏好可能左右评价结果等问题。在以后的研究中应克服以上问题，进一步完善 GC-TOPSIS， 使其更具有普遍适应性。 参考文献 [1] 马丽娟. 基于供应链管理的供应商选择问题初探[J]. 工业工程与管理, 2002, 6: 23-25. [2] 姜灵敏. 理想解法及其在商业银行经营绩效综合评价中的应用[J]. 系统工程理论方法应用, 2002, 11(3): [3] 方世建, 华武, 陈刚. 安徽工业经济效益 TOPSIS 法分析研究[J]. 预测, 2003, 3: 77-80. [4] 陈雷, 王延章. 基于熵权系数与 TOPSIS 集成评价决策方法的研究[J]. 控制与决策, 2003, 18(4): 227-230. 456-459. [5] 于洋, 李一军. 基于多策略评价的绩效指标权重确定方法研究[J]. 系统工程理论与实践, 2003, 8: 8-15. [6] Ma J, Fan Z P, Huang L H. A Subjective and Objective Integrated Approach to Determine Attributes Weights[J]. European J of Operational Research, 1999, 112(2): 397-404. [7] 陈家良. 基于博弈论的组合赋权评价方法研究[J]. 福建电脑, 2003, 9: 15-16. [8] 刘思峰, 郭天榜, 党耀国. 灰色系统理论及其应用[M]. 北京: 科学出版社, 1999. [9] 邓聚龙. 灰色系统理论教程[M]. 武汉: 华中理工大学出版社, 1990. [10] 刘光洁. 灰色决策模型及其在教师素质评价中的应用[J]. 长春师范学院学报, 2004, 1(23): 43-45. Grey Correlation Based on Combinational Weight and Its Application in the Evaluation of Quality of Teacher Fangshan District Commission of Education of Beijing Municipality,Beijing (102488) Chengxi Du,Yue Zhang Abstract Introducing the Grey system theory, this paper presents a new Grey correlation technique for order preference by similarity to ideal solution (GC-TOPSIS) and so as to develop the traditional TOPSIS. First, we decide the weight of every decision - making index by using AHP and entropy method. Second, according to Grey correlation analysis method, we establish GC-TOPSIS by using Grey correlation degree as decision-making unit. Finally, through a evaluation of quality of teacher problem we prove its validity and feasibility. Keywords: AHP；entropy method；traditional TOPSIS；Grey correlation degree；GC-TOPSIS - 7 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料