卡尔曼滤波及其应用(杨金显)13.1.pdf

发布时间：2022-05-31 发布人：admin 分类：说明书资料大小：4.37M 资料格式：pdf 举报版权申诉

liudali000-10805428-4744300845224604096.pdf-第1页.png

第1页 / 共112页

liudali000-10805428-4744300845224604096.pdf-第2页.png

第2页 / 共112页

liudali000-10805428-4744300845224604096.pdf-第3页.png

第3页 / 共112页

liudali000-10805428-4744300845224604096.pdf-第4页.png

第4页 / 共112页

liudali000-10805428-4744300845224604096.pdf-第5页.png

第5页 / 共112页

liudali000-10805428-4744300845224604096.pdf-第6页.png

第6页 / 共112页

liudali000-10805428-4744300845224604096.pdf-第7页.png

第7页 / 共112页

liudali000-10805428-4744300845224604096.pdf-第8页.png

第8页 / 共112页

文本预览

线性系统理论 Kalman滤波及其应用主讲人：杨金显 yangjinxian@hpu.edu.cn 电气工程与自动化学院

Kalman滤波来源在学习卡尔曼滤波之前，首先看看为什么叫“卡尔曼”。跟其他著名的理论（例如傅立叶变换，泰勒级数等等）一样，卡尔曼也是一个人的名字，而跟他们不同的是，他是个现代人！ 1959 年起美国大空署即 NASA开始研究载人太空船登月方案，当时提出了两个主要问题： ①中途导航和制导； ②液体燃料助推器大挠度条件下的自动驾驶问题。因这两项研究的工作量都很庞大，无力同时进行，选择了前者作为重点—— 宇宙飞船的测轨问题。导航问题中主要解决对太空船运动状态的估计，量测信息来自三个子系统：飞船装备的惯性测量装置、天文观测仪和地面测轨系统，测轨数据经数据链传送至太空船。估计方法曾试图采用递推加权最小二乘法和维纳滤波方法，均因精度满足不了要求和计算过于繁杂而不得不放弃。 2

Kalman简介 R.E.Kalman，1930年5月19日生于匈牙利布达佩斯，分别于1953年和1954年在马萨诸塞州工业学院电子工程系获得学士学位和硕士学位，1957年获得哥伦比亚大学获博士学位。主要经历：1958~1964年，在巴尔的摩的RIAS任研究数学家。1964~1971年，在斯坦福大学任教授。1971~1992年，在佛罗里达大学任研究生教授和数学系统理论中心主任。自1973年，他在苏黎世担任数学系统理论主席。另外，他还是美国科学院、工程院以及艺术院的成员，也是匈牙利、法国以及俄罗斯科学院的成员。主要奖项： IEEE荣誉金奖（1974 年）、IEEE 百年纪念奖（1984 年）、京都奖（1985年，日本）、美国数学协会的斯蒂尔奖（1987年）以及贝尔曼奖（1997 年）。 3 3

主要内容引言 Kalman滤波发展及应用 Kalman滤波公式 Kalamn滤波实现 Kalman滤波与导航实例：跟踪技术，组合导航，旋翼飞机 4

引言-最优滤波信号：传递和运载信息的时间或空间函数确定性信号：有一类信号的变化规律是既定的，如调幅广播中的载波信号、阶跃信号、脉宽固定的矩形脉冲信号等，它们都具有确定的频谱。随机信号：没有既定的变化规律，在相同的初始条件和环境条件下，信号的每次实现都不一样，如陀螺漂移、海浪、作水平飞行的飞机飞越山区时无线电高度表的输出信号、惯导系统的导航输出误差、 GPS 的 SA 误差等，它们没有确定的频谱。 5

引言-最优滤波滤波：从混合在一起的诸多信号中提取出所需要的信号。确定性信号的滤波？确定性信号具有确定性的频谱，可根据各信号频带的不同，设置具有相应频率特性的滤波器，如低通、高通、带通、带阻滤波器，使有用信号无衰减地通过，使干扰信号受到抑制。这类滤波器可用物理方法实现—模拟滤波器，也可用计算机通过算法实现—数字滤波器。对确定性信号的滤波处理也称常规滤波。 6

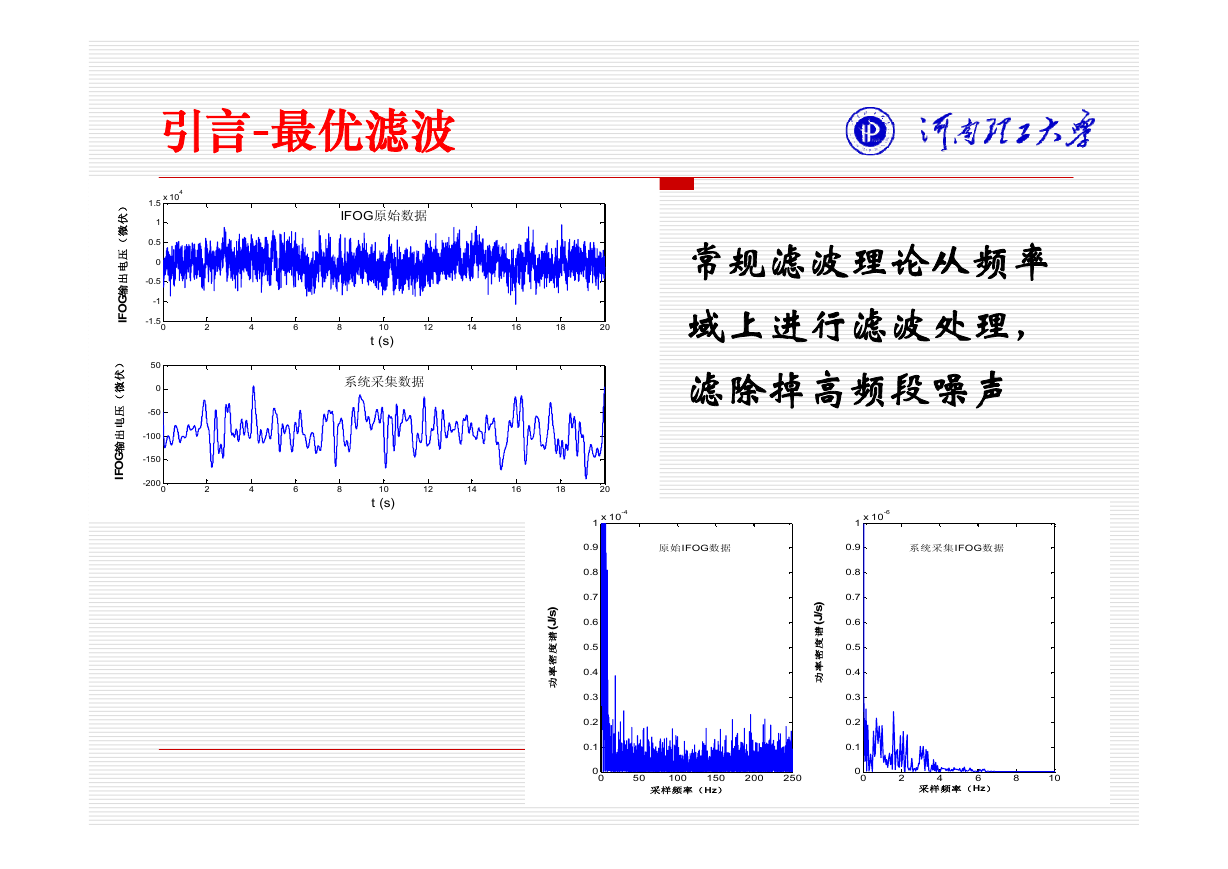
引言-最优滤波）伏微（压电出输 G O F I ）伏微（压电出输 G O F I x 104 1.5 1 0.5 0 -0.5 -1 -1.5 0 50 0 -50 -100 -150 -200 0 IFOG原始数据 2 4 6 8 10 t (s) 12 14 16 18 20 系统采集数据常规滤波理论从频率域上进行滤波处理，滤除掉高频段噪声 2 4 6 8 10 t (s) 12 14 16 18 20 x 10-4 1 x 10-6 1 / ) s J ( 谱度密率功 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 原始IFOG数据系统采集IFOG数据 / ) s J ( 谱度密率功 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 50 100 150 采样频率（Hz） 200 250 0 0 2 4 6 采样频率（Hz） 8 7 10

引言-最优滤波常规的频率域滤波方法无法滤除与有用信号混叠在一起的低频噪声。工程中常见的噪声信号有白噪声和有色噪声信号。白色噪声和有色噪声均为随机信号。 8

分享到：

赞收藏

资料库

卡尔曼滤波及其应用(杨金显)13.1.pdf

相关推荐

人工智能

热门标签

最新资料