logo资料库

2020-2021学年广西河池市南丹县八年级上学期期中数学试题及答案.doc

发布时间：2023-11-19 发布人：admin 分类：说明书 资料大小：0.43M 资料格式：doc 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    2020-2021 学年广西河池市南丹县八年级上学期期中数学试题及答案 本试卷分为三大题 26 小题，满分 120 分，考试用时 120 分钟。 注意：答案一律填写在答题卷上，在试题卷上作答无效 ．．．．．．．．．。 一、选择题(本大题共 12 小题,每小题 3 分,共 36 分)请用 2B 铅笔在答题卷上将选定的答案标号涂黑。 1．下列交通标志是轴对称图形的是 A． B． C． D． 2．如图，在△ABC中，∠A＝80°，点 D在 BC的延长线上，∠ACD＝145°，则∠B是 A．45° C．65° B．55° D．75° 3．已知图中的两个三角形全等，则  的度 数是 A．72° C．58° B．60° D．50° 4．如图，点 E，F在 AC上，AD=BC，DF=BE， 要使△ADF≌△CBE，还需要添加的一个条件是 A．∠A=∠C B．∠D=∠B C．AD∥BC D．DF∥BE 5．下列说法正确的是 A．全等三角形是指形状相同的两个三角形 B．全等三角形是指面积相等的两个三角形 C．两个等边三角形是全等三角形 D．全等三角形是指两个能完全重合的三角形 6．若一个多边形的内角和为 1080°，则这个多边形的边数为 A．6 B．7 C．8 D．9 7．一个三角形三个内角的度数之比为 2∶3∶7,这个三角形一定是 A．等腰三角形 B．直角三角形 C．锐角三角形 D．钝角三角形 8．将一副直角三角尺如图放置，若
    ∠AOD=20°，则∠BOC的大小为 A．140° C．170° B．160° D．150° 9．若等腰三角形的顶角为80 ，则它的一个底角度数为 A． 20 B．50 C．80 D．100 10．如图，已知CD AB ， BE AC ，且 AO 平分 BAC ， 那么图中全等三角形共有 A．2 对 C．4 对 B．3 对 D．5 对 11．已知等腰△ABC的周长为 18cm，BC＝8cm，若 △ABC≌△A′B′C′全等，则△A′B′C′的腰长等于 A．8cm B．2cm或 8cm C．5cm D．8cm或 5cm 12．如图，∠MON=30°，点 1 A A A ，…在 , , 2 3 射线 ON上，点 1 B B B ，…在射线 OM , , 2 3 上，△ 1 A A B ，△ 2 A A B ，△ 3 A A B … 1 3 2 2 4 3 均为等边三角形．若 1 OA = ，则 1 A A B 的边长为 △ 2020 2020 2021 A.2019 B.2020 C. 10102 D. 20192 二、填空题（本大题共 6 小题，每小题 3 分，满分 18 分；只要求填写最后结果.） 13．点 A(3，－2)关于 x轴对称的点的坐标是________． 14．如图，BE，CD是△ABC的高，且 BD＝EC，判定△BCD≌△CBE的依据是“_____”． 15．如图所示，在△ABC中，AE是角平分线，AD是高，∠BAC＝80°，∠EAD＝10°，则∠B的度数为 ． 16．如图△ ABC 中， AD 是 BC 上的中线， BE 是 ABD△ 中 AD 边上的中线，若△ ABC 的面积是 24， 则△ ABE 的面积是________.
    14 题图 15 题图 16 题图 17．如图，△ABC的边 BC的垂直平分线 MN交 AC于 D，若△ADB的周长是 10cm，AB＝4cm，则 AC＝_____cm． 18．如图，在△ABC中，AB=8，AC=6，则 BC边上的中线 AD的取值范围是_________. 17 题图 18 题图 三、解答题（本大题共 8 题，共 66 分；解答应写出必要的文字说明、演算步骤或推理过程.） 19．(6 分)如图，在正方形网格上的一个△ABC，且每个小正方形的边长为 1(其中点 A，B，C均在网格上)． （1）作△ABC关于直线 MN的轴对称图形△A'B'C'； （2）在 MN上画出点 P，使得 PA+PC最小； （3）写出△ABC的面积． 20．(8 分)如图，已知△ABC中，AD⊥BC于点 D，E为 AB边上任意一点， EF⊥BC于点 F，∠1=∠2．求证：DG∥AB．请把证明的过程填写完整． 证明：∵AD⊥BC，EF⊥BC（ ） ∴∠EFB=∠ADB=90°（垂直的定义） ∴EF∥ ∴∠1= （ （ ） ） 又∵∠1=∠2（已知） ∴ （ ）
    ∴DG∥AB（ ） 21．(8 分)如图所示，在△ABC中，D是 BC边上一点∠1=∠2，∠3=∠4，∠BAC=63°，求∠1 和∠DAC的度 数． 22．(8 分)如图，在△ABC中，∠B＝60°，过点 C作 CD∥AB，若∠ACD＝60°. 求证：△ABC是等边三角形. 23．(8 分)一个零件的形状如图，按规定∠A＝90°，∠B和∠C应分别是 32°和 21°，检验工人量得∠BDC ＝149°，就判断这个零件不合格，运用三角形的有关知识说明零件不合格的理由． 24．(8 分)如图，已知 AB＝AE，∠B＝∠E，BC＝ED，AF⊥CD． 求证：F是 CD的中点．
    25．(10 分)如图，∠A＝∠B，AE＝BE，点 D在 AC 边上，∠1＝∠2，AE和 BD 相交于点 O． 求证：△AEC≌△BED 26．(10 分)如图，已知△ABC是边长为 3cm 的等边三角形，动点 P、Q同时从 A,B两点出发(点 P不与点 A,B 重合，点 Q不与点 B,C重合)，分别沿 AB,BC方向匀速移动，它们的速度都是 1cm/s，当点 P到达点 B 时，P,Q两点停止运动，设点 P的运动时间为 ts，则当 t 为何值时，△PBQ是直角三角形？
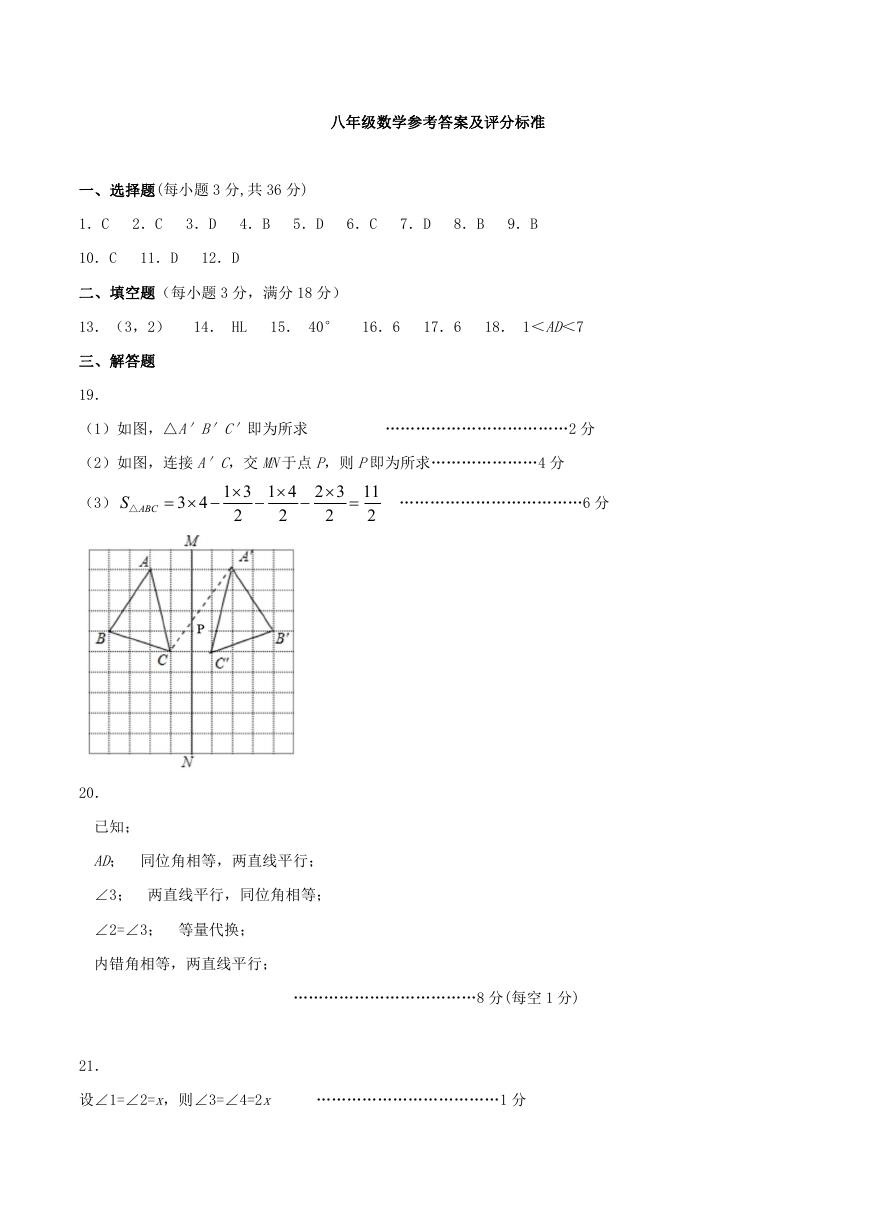
    八年级数学参考答案及评分标准 一、选择题(每小题 3 分,共 36 分) 1．C 2．C 3．D 4．B 5．D 6．C 7．D 8．B 9．B 10．C 11．D 12．D 二、填空题（每小题 3 分，满分 18 分） 13．（3，2） 14． HL 15． 40° 16．6 17．6 18． 1＜AD＜7 三、解答题 19． （1）如图，△A′B′C′即为所求 ………………………………2 分 （2）如图，连接 A′C，交 MN于点 P，则 P即为所求…………………4 分 （3） S △ ABC    3 4 1 3 1 4   2 2   2 3  2  11 2 ………………………………6 分 20． 已知； AD； 同位角相等，两直线平行； ∠3； 两直线平行，同位角相等； ∠2=∠3； 等量代换； 内错角相等，两直线平行； ………………………………8 分(每空 1 分) 21． 设∠1=∠2=x，则∠3=∠4=2x ………………………………1 分
    因为∠BAC=63° 所以∠2＋∠4=117°，即 x＋2x=117°………………………………3 分 所以 x=39°，即∠1=39° ………………………………4 分 所以∠3=∠4=78° ………………………………6 分 ∠DAC=180°－∠3－∠4=24° ………………………………8 分 22． 证法一： ∵ CD∥AB ∴ ∠A＝∠ACD＝60°…………………………3 分 ∵ ∠B＝60° 在△ABC中 ∠ACB＝180°－∠A－∠B＝60°………………5 分 ∴ ∠A＝∠B＝∠ACB ………………………6 分 ∴ △ABC是等边三角形 ……………………8 分 证法二： ∵ CD∥AB， ∴ ∠B＋∠BCD＝180°………………………1 分 ∵ ∠B＝60° ∴ ∠BCD＝120°………………………………2 分 ∴ ∠ACB＝∠BCD－∠ACB＝60° …………3 分 在△ABC中， ∠A＝180°－∠B－∠ACB＝60°………………5 分 ∴ ∠A＝∠B＝∠ACB…………………………6 分 ∴△ABC是等边三角形. ……………………8 分 . 23． 不合格，理由如下 ………………………………1 分
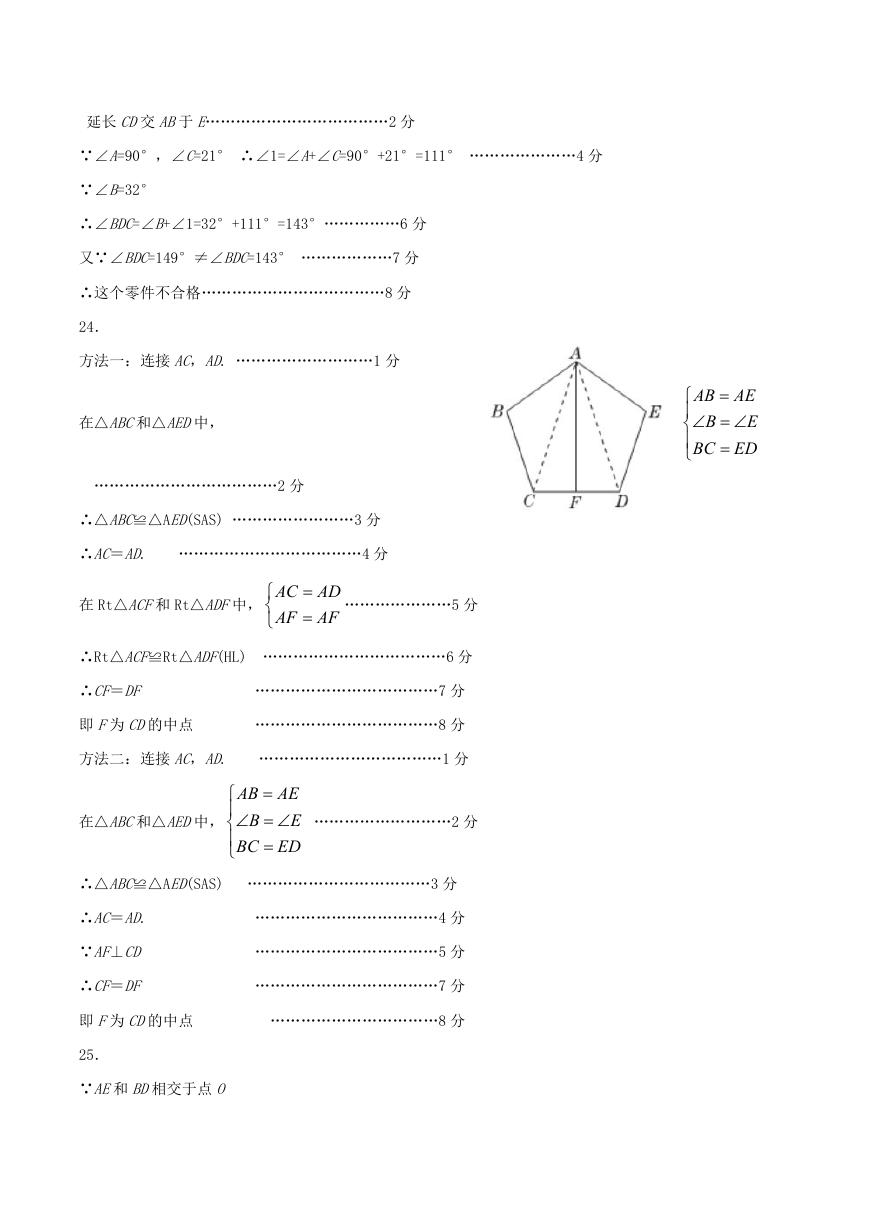
     AB AE     E   BC ED  B  延长 CD交 AB于 E………………………………2 分 ∵∠A=90°，∠C=21° ∴∠1=∠A+∠C=90°+21°=111° …………………4 分 ∵∠B=32° ∴∠BDC=∠B+∠1=32°+111°=143°……………6 分 又∵∠BDC=149°≠∠BDC=143° ………………7 分 ∴这个零件不合格………………………………8 分 24． 方法一：连接 AC，AD. ………………………1 分 在△ABC和△AED中， ………………………………2 分 ∴△ABC≌△AED(SAS) ……………………3 分 ∴AC＝AD. ………………………………4 分 在 Rt△ACF和 Rt△ADF中， AC AD AF AF      …………………5 分 ∴Rt△ACF≌Rt△ADF(HL) ………………………………6 分 ∴CF＝DF ………………………………7 分 即 F为 CD的中点 ………………………………8 分 方法二：连接 AC，AD. ………………………………1 分 在△ABC和△AED中，  AB AE     E   BC ED  B  ………………………2 分 ∴△ABC≌△AED(SAS) ………………………………3 分 ∴AC＝AD. ∵AF⊥CD ∴CF＝DF ………………………………4 分 ………………………………5 分 ………………………………7 分 即 F为 CD的中点 ……………………………8 分 25． ∵AE和 BD相交于点 O
    分享到：
    赞 收藏

    相关推荐

    资料库

    初中二年级

    共收录369份资料，累计95个分类，关注成员有19位，主要包括：2021年,2020年,黑龙江,2022年,贵州,内蒙古,云南,青海,吉林,上海,甘肃,浙江,海南,四川,湖南,广西,山西,山东,辽宁,福建,湖北,河南,河北,江西,广东,安徽,天津,陕西,北京,2019年,江苏

    热门标签

    2021年 2020年 黑龙江 2022年 贵州 内蒙古 云南 青海 吉林 上海 甘肃 浙江 海南 四川 湖南 广西 山西 山东 辽宁 福建 湖北 河南 河北 江西 广东 安徽 天津 陕西 北京 2019年 江苏

    最新资料