logo资料库

基于量子遗传算法的认知无线电频谱分配.pdf

发布时间：2022-06-03 发布人：admin 分类：说明书 资料大小：0.48M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    3  2 1 第 58 卷 第 2 期 2009 年 2 月 1000 58 (02) 3290 2009 1358 06 物 　理 　学 　报 ACTA PHYSICA SINICA Vol. 58 ,No. 2 ,February ,2009 2009 Chin. Phys. Soc. 基于量子遗传算法的认知无线电频谱分配 赵知劲1) 　彭 　振1) 　郑仕链2) 　徐世宇1) 　楼才义2) 　杨小牛2) 1) (杭州电子科技大学通信工程学院 ,杭州 　310018) 2) (中国电子科技集团公司第 36 研究所 ,嘉兴 　314033) (2008 年 4 月 11 日收到 ;2008 年 7 月 5 日收到修改稿) 　　提出了基于量子遗传算法的认知无线电频谱分配算法 ,通过仿真比较了本文算法与颜色敏感图论着色频谱分 配算法的性能. 结果表明基于量子遗传算法的频谱分配算法性能明显优于颜色敏感图论着色算法 ,它能更好地实 现网络效益最大化 ;当用户数和频带数较少时 ,量子遗传算法在进化代数很少时就能找到理想最优解 ,而颜色敏感 图论着色算法所得到的解与理想最优解偏差较大. 关键词 : 认知无线电 , 频谱分配 , 量子遗传算法 , 图论着色 PACC : 9580D 1 引 言 无线频谱是一种宝贵的自然资源. 美国联邦通 信委员 会 ( Federal Communications Commission , 简 称 FCC) 的研究报告[1 ] 表明 ,当前采用的固定频谱分配 政策导致部分频段拥挤不堪 ,而其他频段使用率则 极为低下. 为了缓解无线频谱资源短缺 、频谱利用率 不均的局面 ,人们提出了使用认知无线电技术的动 态频谱共享机制 ,允许认知无线电用户 (也称次用 户) 使用主用户当前未使用的频谱空穴 ,从而提高频 谱利用率[2 ] . 认知无线电通过感知外部无线环境 、智能调整 无线电参数并不断学习来最佳满足 外 部 环 境 需 求[3 ] ,期望实现高可靠性的通信并最大化频谱利用 率[2 ] . 本文着眼于研究频谱空穴检测完成后 ,空闲频 谱资源在次用户间的分配问题. 针对中心式或分布 式的网络体系结构 、协作式或非协作式的频谱分配 行为 、共存式或覆盖式的频谱接入技术[4 ] ,人们提出 了不同的动态频谱分配方法 ,主要包括博弈论[5 —7 ] 、 拍卖理论[8 ] 、议价机制[9 ] 、图论着色[10 —12 ] 等. 文献 [10 ,11 ]提出了一种认知无线电频谱分配模型和基 于图论着色理论的频谱分配算法 ,文献[12 ]则在此 基础上提出了一种并行着色频谱分配算法. 本文在 讨论这种频谱分配模型基础上 ,提出了一种全新的 基于量子遗传算法 ( quantum genetic algorithm , 简称 QGA) 的频谱分配方法 ,通过仿真对基于 QGA 的频 谱分配算法和基于图论着色理论的分配算法性能进 行了比较 ,仿真结果验证了本文所提算法的高效性 和优越性. 2 量子遗传算法 量子遗传算法[3 ,13 —16 ] 是量子计算和遗传算法相 结合的产物 ,其关键步骤包括染色体编码 、种群测 量 、种群更新等. 2 1 染色体编码方式 在 QGA 中 ,染色体编码采用量子位来实现. 量 子位与经典位的不同之处在于它可以落在| 0〉和| 1〉 之外的线性组合态 ,其状态通常表示为 φ〉= α 0〉+ β 1〉, (1) 其中 ,α和β分别表示状态| 0〉和状态| 1〉的概率幅. 对量子位测量时得到 0 的概率为| α| 2 ,得到 1 的概 率为| β| 2 .α和β需要满足归一化条件 | α| 2 +| β| 2 = 1. (2) 　　设一个染色体包含 l 位量子位 ,则其编码形式 为 q = α1 β1 α2 β2 … … αl βl , (3) 浙江省教育厅科技计划项目 (批准号 :20050543) 和电科院预研基金项目 (批准号 :41101040102) 资助的课题. 通讯联系人. E mail :lianshizheng @126 com
    2 期 赵知劲等 : 基于量子遗传算法的认知无线电频谱分配 9531 其中| αj | 2 + | βj | 2 = 1 , j = 1 ,2 , …, l . 采用量子位编 码后 ,QGA 中染色体种群可以表示为 Q ( g) = { qg 1 , p } ,其中 g 表示进化代数 , P 表示种群规模 2 , …, qg qg i ( i = 1 ,2 , …, P) 表示第 g 代种群中 (种群大小) , qg 第 i 个染色体 ,它可表示为 αg i2 βg i2 αg βg … … αg i1 βg i1 qg i = (4) il il . 之 ,则调整量子位使得概率幅对 αij βij 向着有利于 bj 出现的方向演化. 2 4 QGA 基本流程 QGA 基本流程图如图 1 所示. 算法终止条件一 般以是否达到最大进化代数 G 作为衡量标准. 随着 进化的进行 ,种群的解逐渐向最优解收敛. 2 2 种群测量 p } ,其中每一个二进制解 pg 测量将改变量子位的状态 ,使其从| 0〉和| 1〉的 叠加态塌缩到与观测结果相应的特定状态. 对种群 Q ( g) 中的各个个体实施一次测量 ,将得到一组状 态 P ( g) . P ( g) 是一组二进制解 , P ( g) = { pg 1 , pg 2 , i ( i = 1 ,2 , …, P) 均 …, pg i 中第 j 位的 是由长度为 l 的二进制串组成 ,并且 pg i 中第 j 位量子位的概率| αg ij | 2 ( j = 1 ,2 , 取值通过 qg …, l) 确定 ,即随机产生一个[0 ,1 ]之间的数 ,比较其 与| αg i 中相应位 取值为“0”,否则取值为“1”. 适应度评价针对 P ( g) 进行 ,而不是 Q ( g) . ij | 2 的大小 ,如果它小于| αg ij | 2 ,则 pg 2 3 种群更新 初始化种群时 , q0 i 中 的α0 ij 和β0 ij 均 初 始 化 为 2 ,表示在初始搜索时所有状态均以相同的概率 1 进行叠加. QGA 中使用量子门实现种群的进化. 本 文中使用的量子旋转门的更新操作如下所示 : α′ij β′ij = cosθij sinθij - sinθij cosθij αij βij 为 染 色 体 i 第 j 个 量 子 位 , , (5) α′ij β′ij 表 示 其中 , αij βij 更新后的形式 ,θij 表示量子旋转门的旋转角. αij βij 本文采用如下调整策略 :θij =Δθij ·s (αij ,βij ) ,其中 Δθij和 s (αij ,βij ) 分别代表旋转的角度和方向 ,具体 取值与文献[3 ]中一致. 该调整策略将待调整个体当 前的测量值的适应度 f ( pi ) 与已保存的最优解的适 应度 f ( b) 进行比较 ,如果 f ( pi ) > f ( b) ,则调整个 体 i 中相应位的量子位 (该位测量值 pij (二进制串 pi 的第 j 位) 与最优解相应位的值 bj 不相等) ,使得 概率幅对 αij βij 向着有利于 pij 出现的方向演化 ; 反 图 1 　QGA 基本流程 3 基于 QGA 的认知无线电频谱分配 3 1 认知无线电频谱分配模型 认知无线电频谱分配模型[11 ] 由可用频谱矩阵 、 效益矩阵 、干扰矩阵和无干扰分配矩阵描述. 假定 N 为次用户数 ,各个次用户分别用标号 0 ,1 , …, N - 1 表示 , M 为认知无线电可用频带数 ,频带间相互 正交 ,各个频带分别用 0 ,1 , …, M - 1 表示. 可用频谱矩阵是指在某个空间、某个时间主用 户不占用的频谱. 由于主用户地理位置、发射功率等 参数的不同 ,临近次用户对主用户频谱的可用性可 能不同. 例如对于某可用频带 m (0 ≤m ≤M) ,在主
    0631 物 　　理 　　学 　　报 58 卷 用户发射功率覆盖范围以外的次用户可以使用该频 带 ,而在覆盖范围以内的次用户不能使用该频带. 频 谱对于次用户是否空闲用可用频谱矩阵 L 表示 : L = { ln , m | ln , m ∈{0 ,1}} N ×M , ln , m = 1 表示用户 n 可以 使用频带 m , ln , m = 0 表示用户 n 不能使用频带 m. 不同的次用户采用的发射功率、空时特性 、调制 技术等有所不同 ,在不同的频谱上具有不同的传输 效益. 用户获得的效益用效益矩阵 B 表示 : B = { bn , m } N ×M , bn , m 表示用户 n 在频带 m 上获得的效 益 ,如频谱利用率 、最大流量等. 对于某一个可用频带 ,不同的次用户都可能使 用该频带 ,这样用户之间可能会产生干扰. 用户之间 的干扰用干扰矩阵 C 表示 : C = { cn , k , m | cn , k , m ∈{0 , 1}} N ×N ×M , cn , k , m = 1 表示用户 n 和用户 k 同时使用 频带 m 时会产生干扰 , cn , k , m = 0 则表示不会产生干 扰. 当 n = k 时 , cn , n , m = 1 - ln , m . 实际应用中 ,由于 认知无线电系统进行频谱分配的时间相对于频谱环 境变化的时间很短 ,因此假定用户地理位置 、可用频 谱资源等是静态的 ,即矩阵 L , B , C 在一个分配周 期内维持不变. 无干扰分配矩阵 A = { an , m | an , m ∈{0 ,1}} N ×M , an , m = 1 表示频带 m 已经分配给用户 n , an , m = 0 表 示频带 m 没有分配给用户 n. 无干扰分配必须满足 C 定义的如下无干扰约束条件 : an , m + ak , m ≤1 , cn , k , m = 1 , 0 ≤ n , k < N ,0 ≤ m < M. (6) 　　给定某一无干扰频谱分配 ,用户由此获得的总 效益 用 效 益 向 量 表 示 : R = {βn = ∑M - 1 m = 0 an , m · bn , m } N ×1 ,其中βn 表示用户 n 获得的总效益. 认知无 线电频谱分配目标即最大化网络效益 U ( R) , 令 Λ( L , C) N , M 表示无干扰频谱分配矩阵集合 ,则频谱 分配可表示为如下所示的优化问题 : A = arg max N ,M A ∈Λ( L , C) U ( R) , (7) 其中 A U ( R) = ∑N - 1 为最优的无干扰频谱分配矩阵. 本文中 , βn ,即最大化整个网络的效益总和. n = 0 3 2 基于 QGA 的频谱分配算法 本文提出的基于 QGA 的频谱分配算法中 ,每一 条染色体测量后的二进制串表示一种可能的频谱分 配. 由于与可用频谱矩阵 L 中值为 0 的元素位置相 对应的无干扰频谱分配矩阵 A 中的元素值必定为 0 ,若将 A 中所有元素均用量子位表示 ,将使染色体 中包含大量冗余 ,所以本文仅对与 L 中值为 1 的元 素位置对应的 A 中的元素进行量子位编码 ,故染色 体中量子位个数等于 L 中值为 1 的元素个数. 图 2 给出了 N = 5 , M = 6 时的染色体测量值结构示例 , 若 A 中所有元素均用一个量子位进行编码 ,则所需 量子位数为 30 ,由于 A 需要满足 L 的约束限制 ,仅 将加下划线的元素映射为量子位 ,则量子位数仅为 9. 初始种群中概率幅均初始化为 1 2 ,随着进化的 进行根据 (5) 式不断更新 ,图 1 中 pi = [ 0 ,1 ,1 ,0 ,1 , 1 ,0 ,1 ,0 ]为初始种群中第 i 个染色体的测量值. 对 染色体测量值进行适应度评价时需要将其映射为 A ,本文直接将测量值的每一位按行逐个填充到与 L 中值为 1 的元素位置相对应的 A 的元素 ,如图 2 中箭头所示 ,由此得到了一种频谱分配. 图 2 　染色体测量值结构示例 　　量子位测量值取 0 或 1 由概率幅决定 ,并不一 定满足 (6) 式定义的无干扰约束条件. 本文对量子位 染色体测量值进行如下无干扰约束处理 :对任意频 带 m (0 ≤m < M) ,寻找满足 cn , k , m = 1 的所有 n 和 k ,检查 A 中第 m 列第 n 行和第 m 列第 k 行元素对 应的量子位测量值是否均为 1 ,若是 ,随机将其中一 位置 0 ,另一位保持不变. 经以上处理后 ,染色体测 量值满足无干扰约束 ,因此测量值代表了一种可行
    2 期 的频谱分配. 赵知劲等 : 基于量子遗传算法的认知无线电频谱分配 1631 衡量染色体测量值性能的适应度函数与目标函 数相对应 ,由于频谱分配所要实现的目标是最大化 网络效益 U ( R) ,故本文直接将 U ( R) 作为适应度 函数. 随着进化的进行 ,种群中个体测量值适应度不 断增加 , 达到最大迭代次数时 , 算法终止 , 此时将 B ( g) 保存的解映射为 A 的形式 ,即得到了最佳的 频谱分配. 综上所述 ,本文提出的基于 QGA 的频谱分配算 法的流程如下 : 1) 给定可用频谱矩阵 L = { ln , m | ln , m ∈{0 , 1}} N ×M ,效益矩阵 B = { bn , m } N ×M 和干扰矩阵 C = { cn , k , m | cn , k , m ∈{0 ,1}} N ×N ×M ,确定种群规模 P ,确 N M ∑ ln , m ,记录 L 中值为 1 定染色体量子位数 l = ∑ 的元素对应的 n 与 m ,即令 L 1 = { ( n , m) | ln , m = 1} 且使 L 1 中元素按照 n 递增 、m 递增方式排列 , L 1 中 元素个数为 l. m = 1 n = 1 2) 令 g = 0 ,初始化种群 Q ( g) = { qg 1 , qg 2 , …, qg P}. 1 , pg 4) 将 pg 2 , …, pg 一组状态 (染色体测量值) P ( g) = { pg 3) 对 Q ( g) 中的每个个体实施一次测量 ,得到 P}. i ( i = 1 ,2 , …, P) 的第 j 位映射为 an , m , 其中 ( n , m) 为 L 1 中第 j 个元素 ( j = 1 ,2 , …, l) ;对 所有 m (0 ≤m < M) ,寻找满足 cn , k , m = 1 的所有 n 和 k ,检查 A 中第 m 列第 n 行和第 m 列第 k 行元素 对应的两位测量值是否均为 1 ,若是 ,随机将其中一 位设置为 0 ,另一位保持不变. 5) 对 P ( g) 进行适应度评价 ,将 P ( g) 中最优解 保存至 B ( g) . 6) 如果达到最大进化次数 ,算法终止 ,将 B ( g) 中保存的二进制串映射为 A 的形式 ,即得到了最佳 的频谱分配 ;否则 ,继续. 7) g = g + 1. 8) 对种群 Q ( g - 1) 实施一次测量 ,得到一组状 态 P ( g) = { pg 1 , pg 2 , …, pg P}. 10) 运用适应度函数对 P ( g) 进行适应度评价. 11) 将 P ( g) 和 B ( g - 1) 中的最优解保存至 B ( g) . 12) 使 用 量 子 旋 转 门 对 种 群 进 行 更 新 , 得 到 Q ( g) ,转至 6) . 4 性能仿真及结果分析 针对 3 1π至 0 1 节所述频谱分配模型 ,目前研究人员 主要采用图论着色理论来解决 ,并且将相应算法称 为颜 色 敏 感 图 论 着 色 算 法 ( color sensitive graph coloring ,简称 CSGC) [10 —12 ] . 本文仿真中对基于 QGA 的频谱分配算法和 CSGC 算法性能进行了比较. 005π间 QGA 参数取值为 P = 20 ,Delta 在 0 动态变化 (随进化代数线性递减) ,最大进化代数为 50. 图 3 给出了当 N = 20 , M = 22 时不同的初始条件 下的实验结果 ,不同实验中 B , L , C 不同 ,同一次实 验中 CSGC 算法和本文提出的基于 QGA 的频谱分配 算法所采用的 B , L , C 相同 , B , L , C 根据文献[11 ] 附录 Ⅰ提供的伪码仿真产生. 从图中可以看出 ,50 次实验中基于 QGA 的频谱分配算法所得到的网络 效益多数明显大于 CSGC 获得的网络效益 ,仅有少 数点较为接近 ,说明了基于 QGA 的频谱分配算法的 有效性和优越性. 图 3 　QGA 和 CSGC 性能比较 9) 将 pg i ( i = 1 ,2 , …, P) 的第 j 位映射为 an , m , 其中 ( n , m) 为 L 1 中第 j 个元素 ( j = 1 ,2 , …, l) ;对 所有 m (0 ≤m < M) ,寻找满足 cn , k , m = 1 的所有 n 和 k ,检查 A 中第 m 列第 n 行和第 m 列第 k 行元素 对应的两位测量值是否均为 1 ,若是 ,随机将其中一 位置 0 ,另一位保持不变. 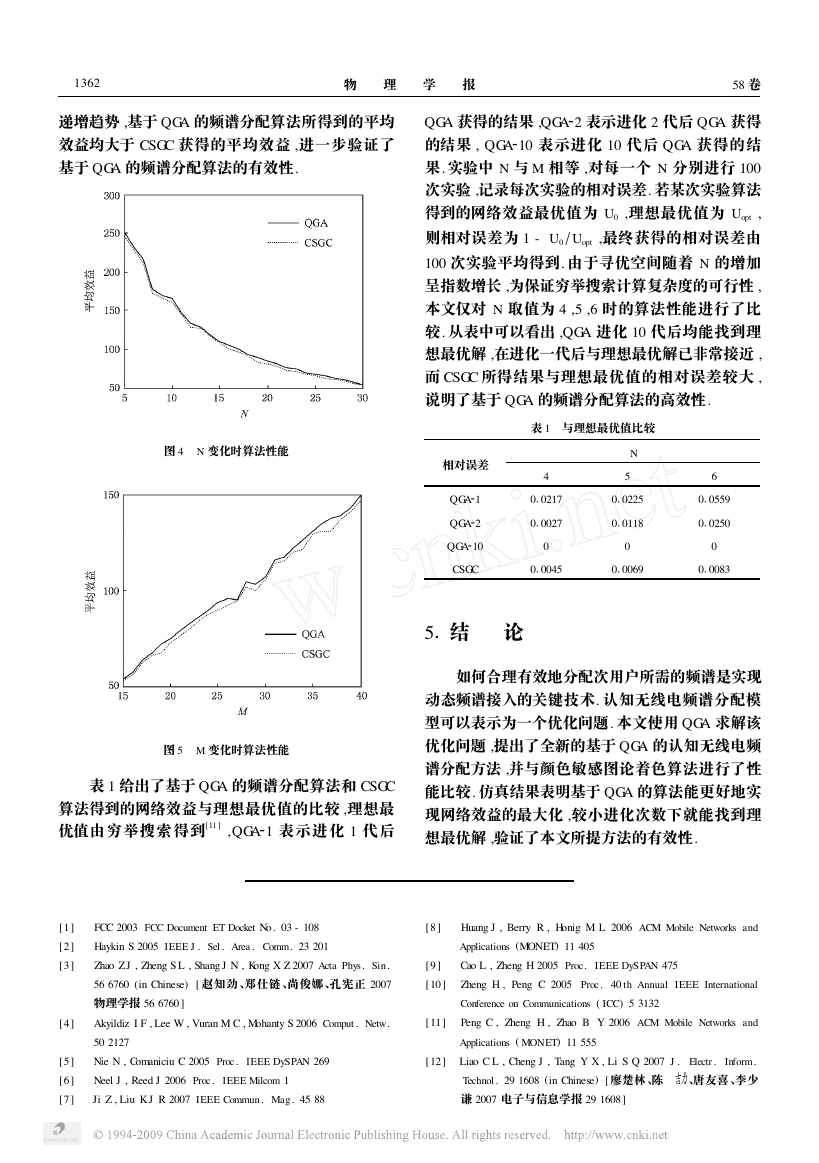图 4 给出了 M = 30 时平均效益随次用户数 N 的变化曲线 ,平均效益等于网络效益除以 N . 由图 3 可知 ,随着 N 的增加 ,平均效益呈递减趋势. 基于 QGA 的频谱分配算法所得到的平均效 益 均 大 于 CSGC. 图 5 给出了 N = 15 时平均效益随可用频谱数 M 的变化曲线. 随着频带数 M 的增加 ,平均效益呈
    2631 物 　　理 　　学 　　报 58 卷 递增趋势 ,基于 QGA 的频谱分配算法所得到的平均 效益均大于 CSGC 获得的平均效益 ,进一步验证了 基于 QGA 的频谱分配算法的有效性. 图 4 　N 变化时算法性能 图 5 　M 变化时算法性能 表 1 给出了基于 QGA 的频谱分配算法和 CSGC 算法得到的网络效益与理想最优值的比较 ,理想最 优值由穷举搜索得到[11 ] ,QGA 1 表示进化 1 代后 2 表示进化 2 代后 QGA 获得 QGA 获得的结果 ,QGA 的结果 , QGA 10 表示进化 10 代后 QGA 获得的结 果. 实验中 N 与 M 相等 ,对每一个 N 分别进行 100 次实验 ,记录每次实验的相对误差. 若某次实验算法 得到的网络效益最优值为 U0 ,理想最优值为 Uopt , 则相对误差为 1 - U0 Uopt ,最终获得的相对误差由 100 次实验平均得到. 由于寻优空间随着 N 的增加 呈指数增长 ,为保证穷举搜索计算复杂度的可行性 , 本文仅对 N 取值为 4 ,5 ,6 时的算法性能进行了比 较. 从表中可以看出 ,QGA 进化 10 代后均能找到理 想最优解 ,在进化一代后与理想最优解已非常接近 , 而 CSGC 所得结果与理想最优值的相对误差较大 , 说明了基于 QGA 的频谱分配算法的高效性. 表 1 　与理想最优值比较 4 0 0 0217 0027 0 N 5 0 0 0225 0118 0 0 0045 0 0069 相对误差 QGA 1 QGA 2 QGA 10 CSGC 6 0 0 0559 0250 0 0 0083 5 结 　论 如何合理有效地分配次用户所需的频谱是实现 动态频谱接入的关键技术. 认知无线电频谱分配模 型可以表示为一个优化问题. 本文使用 QGA 求解该 优化问题 ,提出了全新的基于 QGA 的认知无线电频 谱分配方法 ,并与颜色敏感图论着色算法进行了性 能比较. 仿真结果表明基于 QGA 的算法能更好地实 现网络效益的最大化 ,较小进化次数下就能找到理 想最优解 ,验证了本文所提方法的有效性. [1 ] [2 ] [3 ] [4 ] [5 ] [6 ] [7 ] FCC 2003 FCC Document ET Docket No. 03 - 108 Haykin S 2005 IEEE J . Sel . Area. Comm. 23 201 Zhao ZJ , Zheng S L , Shang J N , Kong X Z 2007 Acta Phys. Sin. [ 赵知劲、郑仕链、尚俊娜、孔宪正 2007 56 6760 (in Chinese) 物理学报 56 6760 ] Akyildiz I F , Lee W , Vuran M C , Mohanty S 2006 Comput . Netw. 50 2127 Nie N , Comaniciu C 2005 Proc. IEEE DyS PAN 269 Neel J , Reed J 2006 Proc. Ji Z , Liu KJ R 2007 IEEE Commun. Mag. 45 88 IEEE Milcom 1 [8 ] [9 ] [10 ] [11 ] Huang J , Berry R , Honig M L 2006 ACM Mobile Networks and Applications (MONET) 11 405 Cao L , Zheng H 2005 Proc. IEEE DyS PAN 475 Zheng H , Peng C 2005 Proc. 40 th Annual IEEE International Conference on Communications ( ICC) 5 3132 Peng C , Zheng H , Zhao B Y 2006 ACM Mobile Networks and Applications ( MON ET) 11 555 [12 ] Liao C L , Cheng J , Tang Y X , Li S Q 2007 J . Electr. Inform. Technol . 29 1608 (in Chinese) [ 廖楚林、陈 　　、唐友喜、李少 谦 2007 电子与信息学报 29 1608 ]
    3  2 1 2 2 期 赵知劲等 : 基于量子遗传算法的认知无线电频谱分配 3631 [13 ] Narayanan A , Moore M 1996 IEEE International Conference on [15 ] Yan J A , Zhuang Z Q 2003 J . Electron. 20 62 [14 ] Han K H , Kim J H 2000 IEEE International Conference on Evolutionary Computation 61 Evolutionary Computation 1354 [16 ] Zhou S , Pan W , Luo B , Zhang W L , Ding Y 2006 Acta Electron. Sin. 34 897 (in Chinese) [ 周 　殊、潘 　炜、罗 　斌、张伟利、丁 　莹 2006 电子学报 34 897 ] Cognitive radio spectrum a ssignment ba sed on quantum genetic algorithm Zhao Zhi Jin1) 　Peng Zhen1) 　Zheng Shi Lian2) 　Xu Shi Yu1) 　Lou Cai Yi2) 　Yang Xiao Niu2) 1) ( Telecommunication School , Hangzhou Dianzi University , Hangzhou 　310018 , China) 2) ( The 36 th Research Institute of China Electronic Technology Group Corporation , Jiaxing 　314033 , China) (Received 11 April 2008 ; revised manuscript received 5 July 2008) Abstract Cognitive radio spectrum assignment based on quantum genetic algorithm is proposed , and simulations are conducted to compare the proposed method with color sensitive graph coloring algorithm. Results show that the proposed method greatly outperforms the color sensitive graph coloring algorithm as it better optimizes network utilization. The proposed method can find the optimal solutions after only several generations , while the relative differences between solutions obtained by color sensitive graph coloring algorithm and the optimal solutions are quite large. Keywords : cognitive radio , spectrum assignment , quantum genetic algorithm , graph coloring PACC : 9580D Project supported by the Science and Technology Program of the Education Department of Zhejiang Province , China ( Grant No. 20050543) and the Pre Research Foundation of Electronics Science Research Institute , China ( Grant No. 41101040102) Corresponding author. E mail : lianshizheng @126 com
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料