logo资料库

经典的滤波电路(值得收藏).ppt

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.92M 资料格式：ppt 举报 版权申诉
第1页 / 共24页
第2页 / 共24页
第3页 / 共24页
第4页 / 共24页
第5页 / 共24页
第6页 / 共24页
第7页 / 共24页
第8页 / 共24页
资料共24页，剩余部分请下载后查看
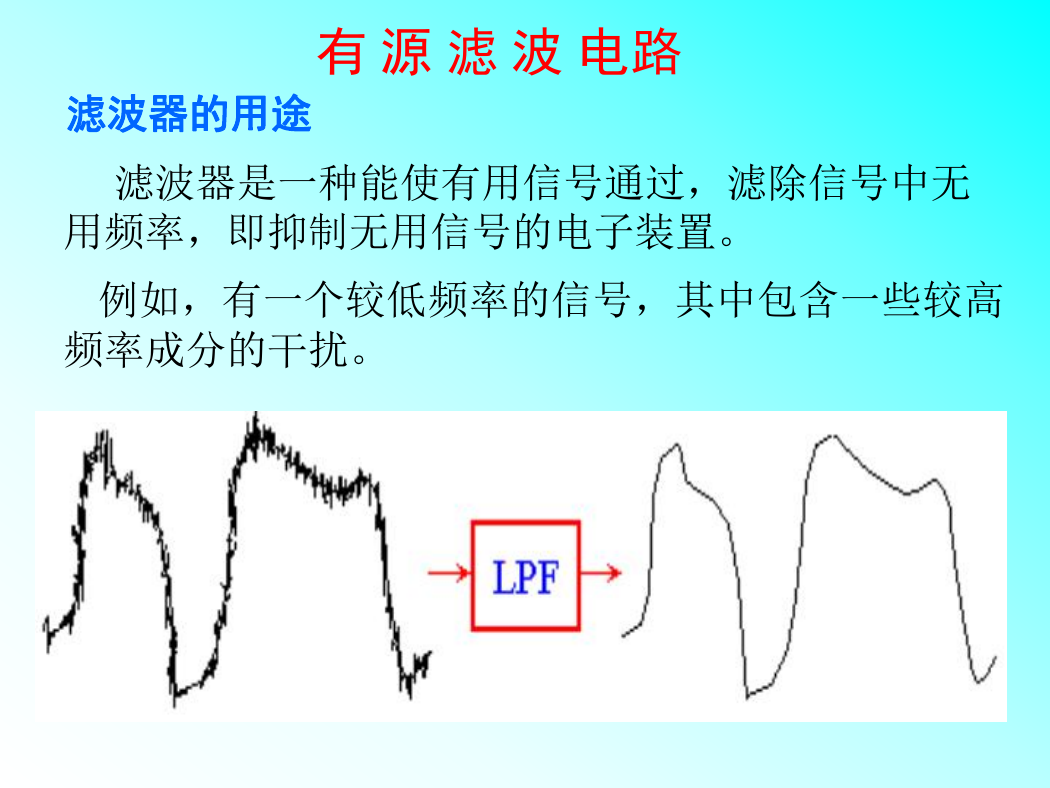
    有 源 滤 波 电路 滤波器的用途 滤波器是一种能使有用信号通过，滤除信号中无 用频率，即抑制无用信号的电子装置。 例如，有一个较低频率的信号，其中包含一些较高 频率成分的干扰。
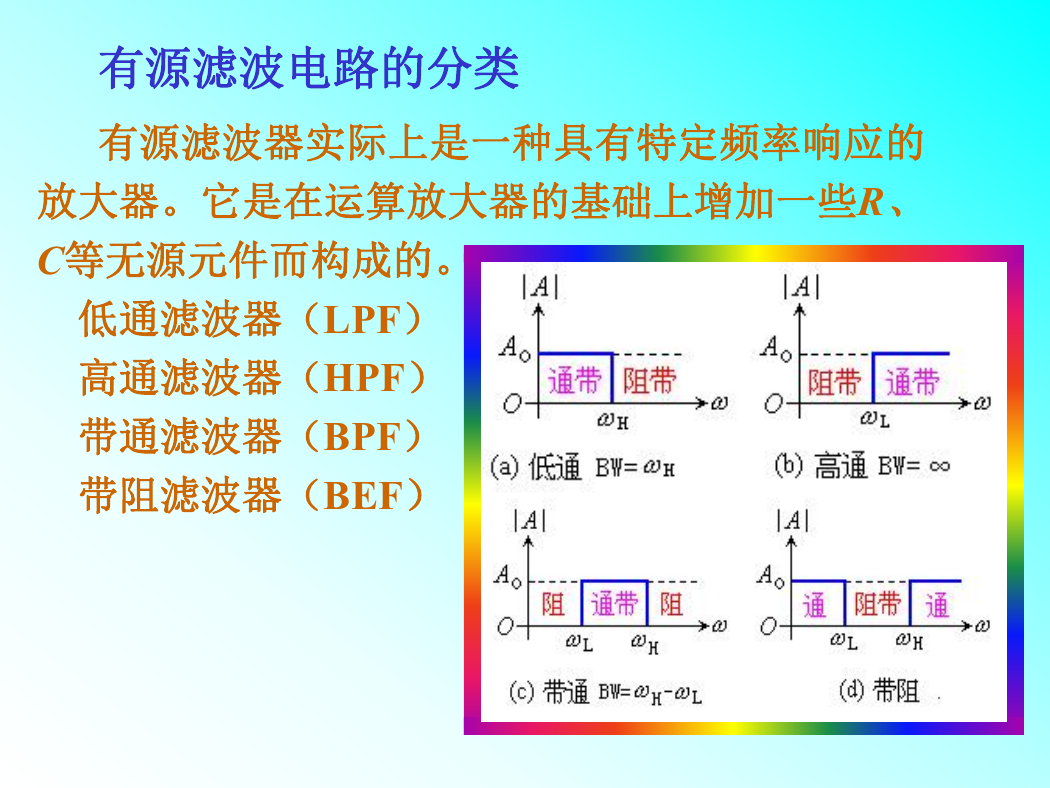
    有源滤波电路的分类 有源滤波器实际上是一种具有特定频率响应的 放大器。它是在运算放大器的基础上增加一些R、 C等无源元件而构成的。 低通滤波器（LPF） 高通滤波器（HPF） 带通滤波器（BPF） 带阻滤波器（BEF）
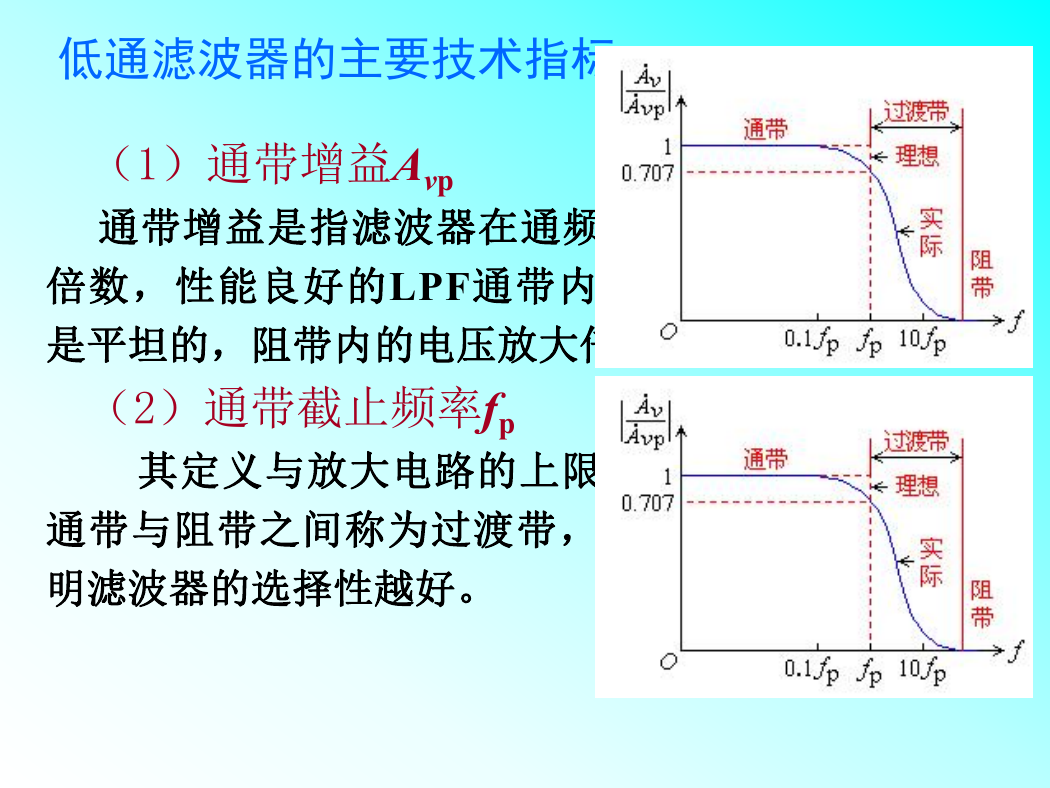
    低通滤波器的主要技术指标 （1）通带增益Avp 通带增益是指滤波器在通频带内的电压放大 倍数，性能良好的LPF通带内的幅频特性曲线 是平坦的，阻带内的电压放大倍数基本为零。 （2）通带截止频率fp 其定义与放大电路的上限截止频率相同。 通带与阻带之间称为过渡带，过渡带越窄，说 明滤波器的选择性越好。
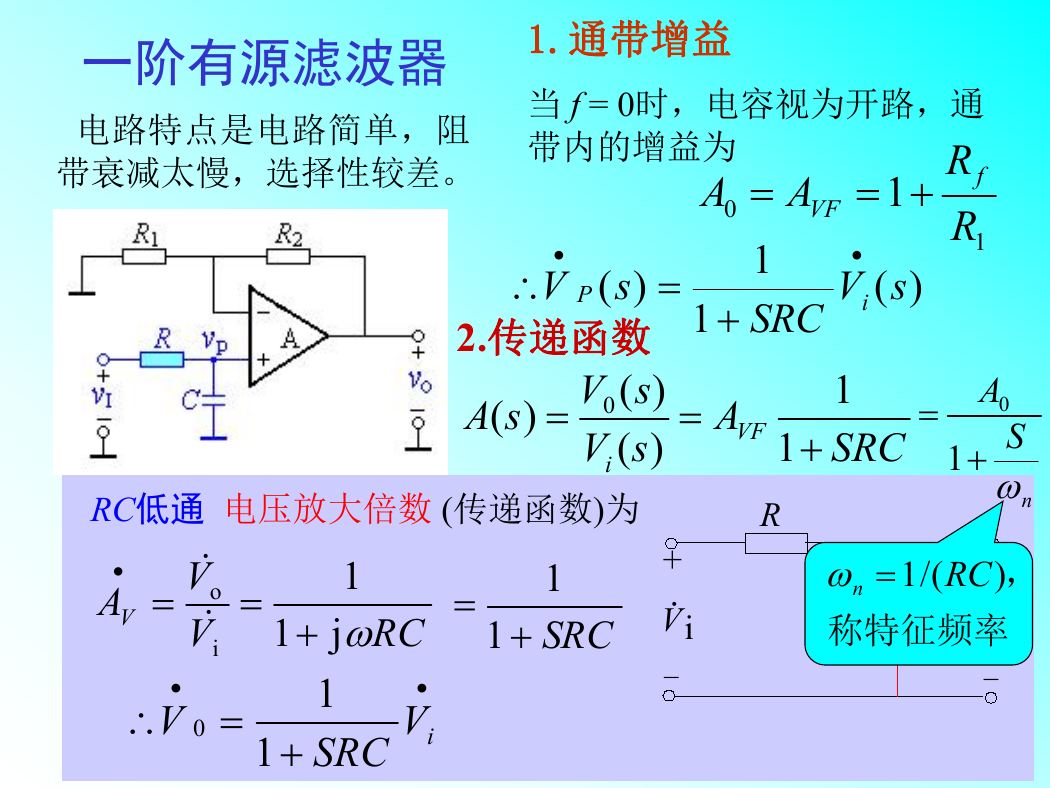
    一阶有源滤波器 电路特点是电路简单，阻 带衰减太慢，选择性较差。 P   )( sV 2.传递函数 )( sV )( sA 0 )( sV i RC低通 电压放大倍数 (传递函数)为   AV   V o  V i  V  0  1 j1  1 SRC  1 RC  iV  1  1 SRC 1.通带增益 当 f = 0时，电容视为开路，通 带内的增益为 R f A 0 R 1 A VF 1   )( sV i  1 SRC  1   + . V i - 1 SRC   A 0 S   n 1 A VF 1 R + ，) /(1 RC n  . C V o 称特征频率 -
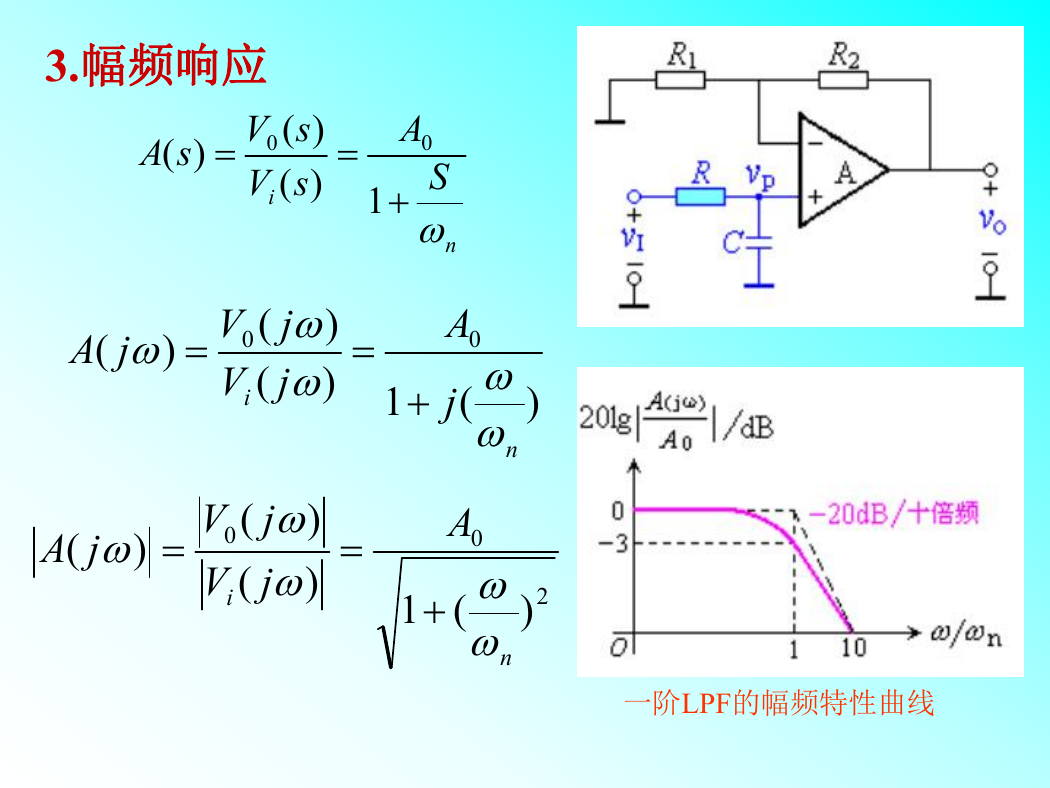
    3.幅频响应  )( sA )( sV 0 )( sV i  A 0 S   n 1 ( jA )   ( jV 0 ( jV i )  )   1  A 0  ( j  n ) ( jA )   ( jV 0 ( jV i )  )   A 0   n (1  2 ) 一阶LPF的幅频特性曲线
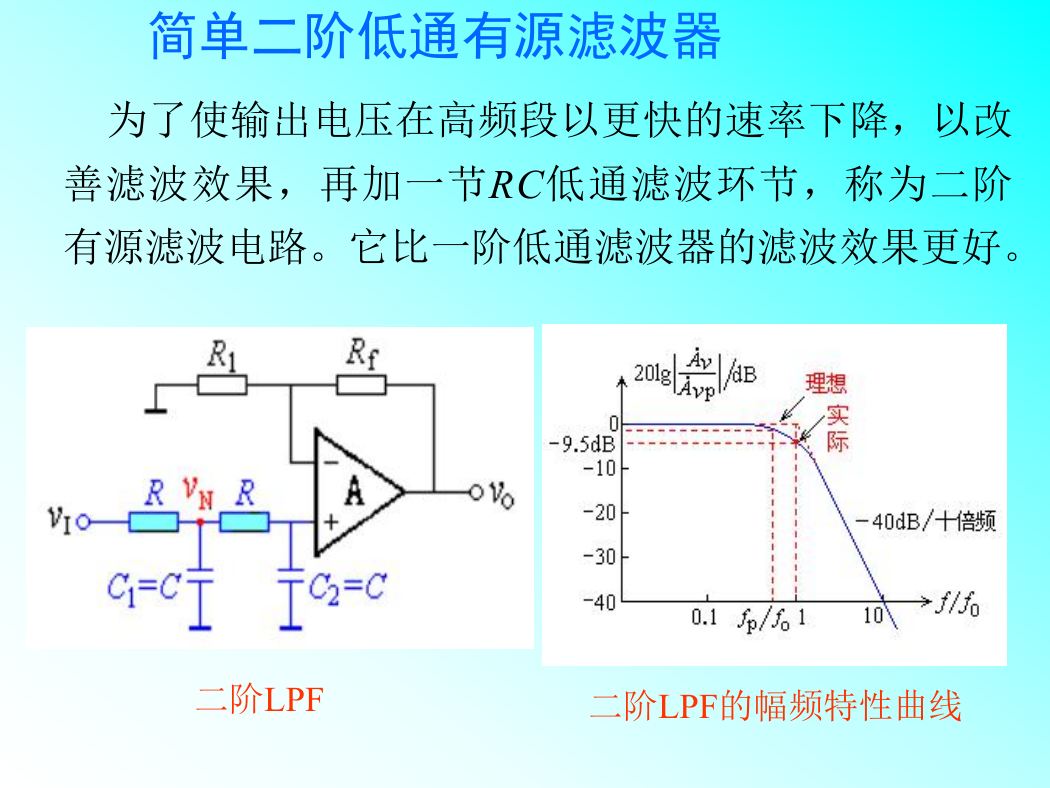
    简单二阶低通有源滤波器 为了使输出电压在高频段以更快的速率下降，以改 善滤波效果，再加一节RC低通滤波环节，称为二阶 有源滤波电路。它比一阶低通滤波器的滤波效果更好。 二阶LPF 二阶LPF的幅频特性曲线
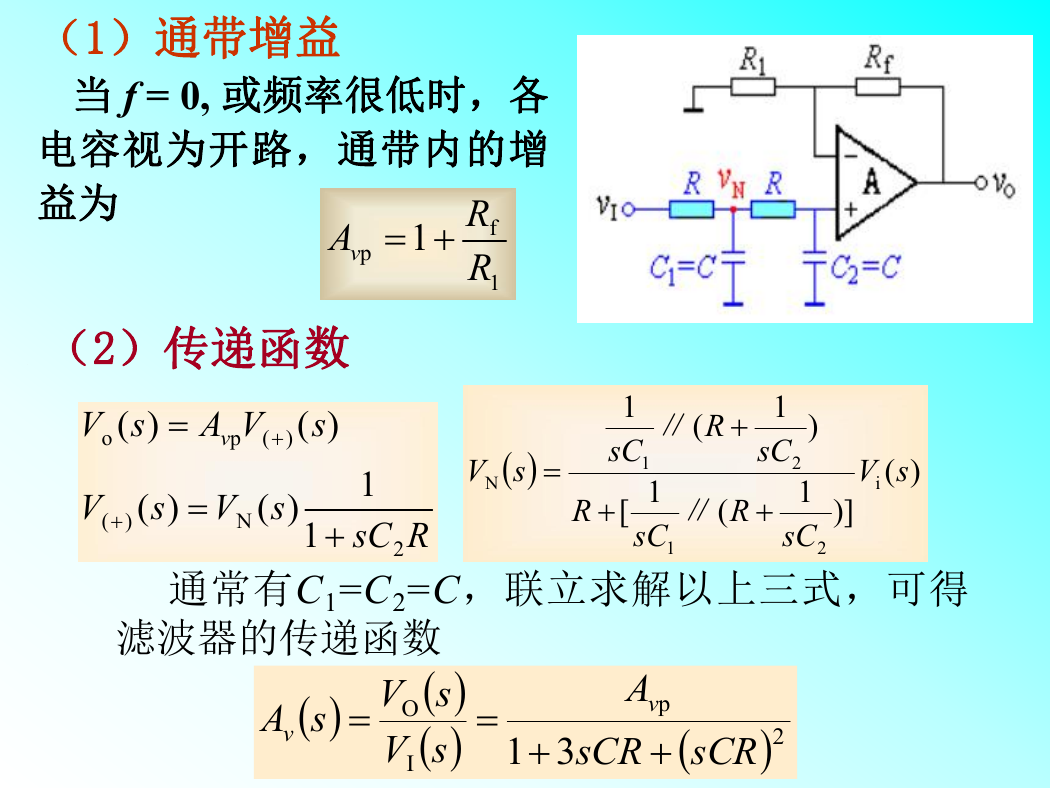
    （1）通带增益 当 f = 0, 或频率很低时，各 电容视为开路，通带内的增 益为 Av p 1  R f R 1 （2）传递函数 )( sV o  VA (p v  ) )( s V (  )( s  )( sV N   sV N  1 RsC 2 1 ∥ sC 1 1[  sC 1 R ( R  ∥ ( R 2 )1 sC )]1  sC 2 )( sV i 1  ) 通常有C1=C2=C，联立求解以上三式，可得 滤波器的传递函数   sV O   sV I A p v sCR    sA v 31  sCR 2   
    (3)通带截止频率 将s换成 jω，令 ,可得 0 RC π2 /1  f 0   A v (1  A v 2 ) p  f f 0 当 时，上式分母的模 f  pf (1  f f 0  j3 f f p 0 2 2 )  j3 p 0 f f 7 f p f 0 f 0   37.0 53  2 解得截止频率 37.0 π2 RC 与理想的二阶波特图相比，在超过 以后， 幅频特性以-40 dB/dec的速率下降，比一阶的 下降快。但在通带截止频率 之间幅频 特性下降的还不够快。 f  p 0f  f 0
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料