模式识别实验二.doc-资料库

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第1页.png

第1页 / 共12页

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第2页.png

第2页 / 共12页

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第3页.png

第3页 / 共12页

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第4页.png

第4页 / 共12页

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第5页.png

第5页 / 共12页

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第6页.png

第6页 / 共12页

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第7页.png

第7页 / 共12页

ef2b6e93-6cce-41a1-a493-3e5b10f254b1.doc.pdf-第8页.png

第8页 / 共12页

大连东软信息学院电子工程系学生实验报告课程名称：___ Bayes 分类器设计______________ 专业班级：___智能 15001_________ 姓名：___朱晓东___________ 学号：__15160700106________________ -- 学年第学期

大连东软信息学院电子工程系实验报告注意事项 1. 课前必须认真预习实验，认真书写预习报告，了解实验步骤，未预习或预习达不到要求的学生不准参加实验； 2. 实验完毕，必须将结果交实验指导教师进行检查，并将计算机正常关机、将仪器设备、用具及椅子等整理好，方可离开实验室； 3. 按照实验要求书写实验报告，条理清晰，数据准确； 4. 当实验报告写错后，不能撕毁，请在相连的实验报告纸上重写； 5. 实验报告严禁抄袭，如发现抄袭实验报告的情况，则抄袭者与被抄袭者该次实验以 0 分计； 6. 无故缺实验者，按学院学籍管理制度进行处理； 7. 课程结束后实验报告册上交实验指导教师，并进行考核与存档。

大连东软信息学院电子工程系实验名称实验目的及要求实验内容及原理实验项目(二 ) — 预习报告 Bayes 分类器设计能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识，理解二类分类器的设计原理。最小风险贝叶斯决策可按下列步骤进行： (1)在已知 ( iP  ， ) ( iXP  ，i=1,…，c 及给出待识别的 X 的情况下，根据贝 ) 叶斯公式计算出后验概率： ) P )  i ( i P (  i X ) ( XP  c  ( XP j 1  )  i P ( ) i j=1,…，x (2)利用计算出的后验概率及决策表，按下面的公式计算出采取 ia ,i=1,…，a 的条件风险 ( XaR i )  c  j 1   j P a ( ) ( , j i X ) ,i=1,2,…,a (3)对(2)中得到的 a 个条件风险值 ( XaR i ) ,i=1,…，a 进行比较，找出使其条件风险最小的决策 ka ，即  R a x  R a x   k i min 1, a i    则 ka 就是最小风险贝叶斯决策。假定某个局部区域细胞识别中正常（ 1）和非正常（ 2 ）两类先验概率分别为正常状态：P（ 1）=0.9；异常状态：P（ 2 ）=0.1。现有一系列待观察的细胞，其观察值为 x ： -3.9847 -3.5549 -1.2401 -0.9780 -0.7932 -2.8531 -2.7605 -3.7287 -3.5414 -2.2692 -3.4549 -3.0752 -3.9934 2.8792 -0.9780 0.7932 1.1882 3.0682

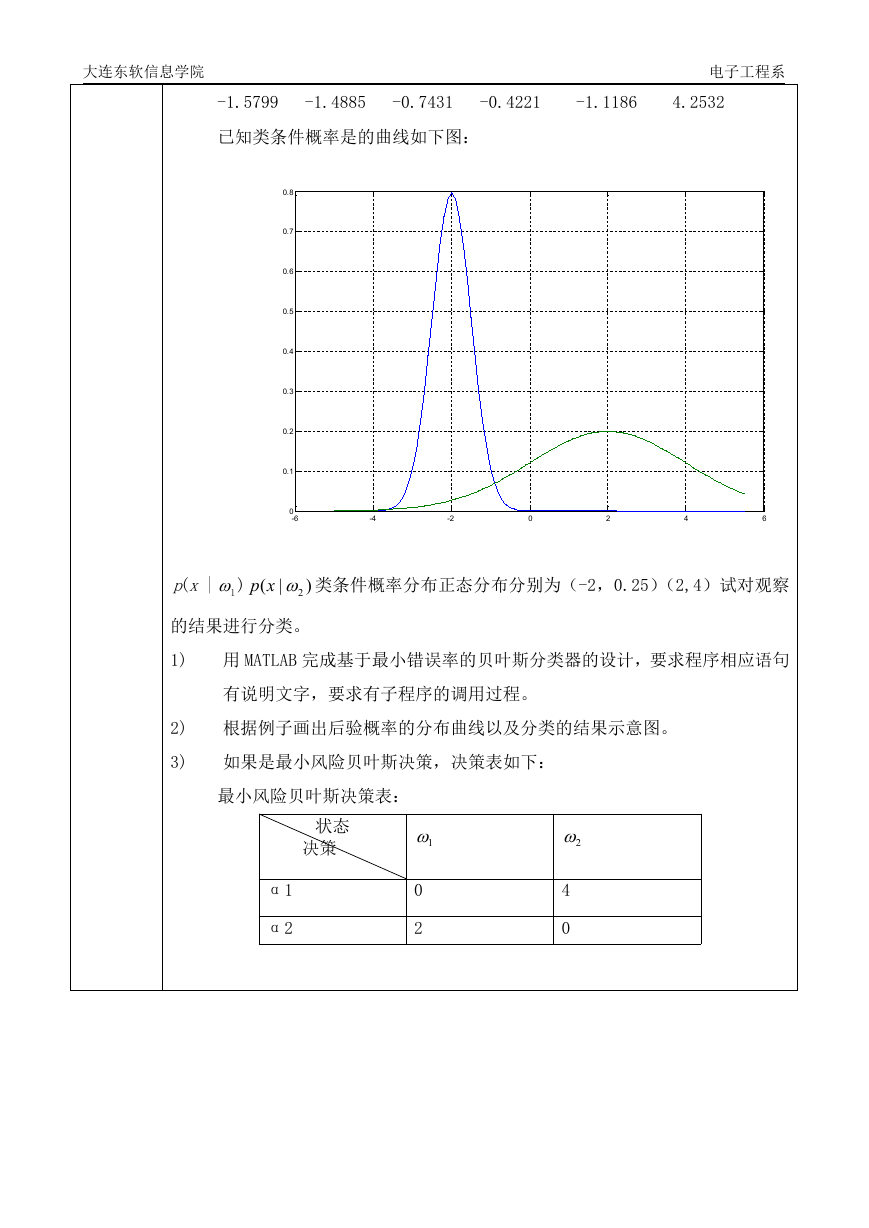
大连东软信息学院电子工程系 -1.5799 -1.4885 -0.7431 -0.4221 -1.1186 4.2532 已知类条件概率是的曲线如下图： 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -6 -4 -2 0 2 4 6 1xp |( ) ( 2xp | ) 的结果进行分类。类条件概率分布正态分布分别为（-2，0.25）（2,4）试对观察 1) 用 MATLAB 完成基于最小错误率的贝叶斯分类器的设计，要求程序相应语句有说明文字，要求有子程序的调用过程。 2) 根据例子画出后验概率的分布曲线以及分类的结果示意图。 3) 如果是最小风险贝叶斯决策，决策表如下：最小风险贝叶斯决策表：状态决策 α1 α2 1 0 2 2 4 0

大连东软信息学院电子工程系预习过程中的疑问实验名称实验室分组情况实验步骤（算法、代码、方法等）实验项目( ) — 实验报告 Bayes 分类器设计指导教师赵秀洁实验日期成绩 -1.2401 -0.9780 -0.7932 -2.8531 -3.0752 3.0682 -3.4549 1.1882 -1.1186 4.2532 ]; -3.5549 -3.7287 2.8792 -1.4885 -2.2692 0.7932 -0.4221 -3.5414 -0.9780 -0.7431 x=[-3.9847 -2.7605 -3.9934 -1.5799 pw1=0.9; pw2=0.1; e1=-2; a1=0.5; e2=2; a2=2 ;%ÀàÌõ¼þ¸ÅÂÊ·Ö²¼ m=numel(x);%µÃµ½´ý²âÏ¸°û¸öÊý pw1_x=zeros(1,m) ;%´æ·Å¶Ôw1µÄºóÑé¸ÅÂÊ¾ØÕó pw2_x=zeros(1,m) ;%´æ·Å¶Ôw2µÄºóÑé¸ÅÂÊ¾ØÕó result=zeros(1,m) ;%´æ·Å±È½Ï½á¹û¾ØÕó %ÀàÌõ¼þ¸ÅÂÊ·þ´ÓÕýÌ¬·Ö²¼ for i=1:m

大连东软信息学院 %¼ÆËãw1ÏÂµÄºóÑé¸ÅÂÊ 电子工程系 pw1_x(i)=(pw1*normpdf(x(i),e1,a1))/(pw1*normpdf(x(i),e1,a1)+pw2*normp df(x(i),e2,a2)); %¼ÆËãw2ÏÂµÄºóÑé¸ÅÂÊ pw2_x(i)=(pw2*normpdf(x(i),e2,a2))/(pw1*normpdf(x(i),e1,a1)+pw2*normp df(x(i),e2,a2)); end if pw1_x(i)>pw2_x(i)%±È½ÏÁ½ÀàºóÑé¸ÅÂÊ result(i)=0 ;%Õý³£Ï¸°û for i=1:m else end result(i)=1 ;%Òì³£Ï¸°û end a=[-5:0.05:5] ;%È¡Ñù±¾µãÒÔ»-Í¼ n=numel(a); pw1_plot=zeros(1,n); pw2_plot=zeros(1,n); for j=1:n pw1_plot(j)=(pw1*normpdf(a(j),e1,a1))/(pw1*normpdf(a(j),e1,a1)+pw2*no rmpdf(a(j),e2,a2)); %¼ÆËãÃ¿¸öÑù±¾µã¶Ôw1µÄºóÑé¸ÅÂÊÒÔ»-Í¼ pw2_plot(j)=(pw2*normpdf(a(j),e2,a2))/(pw1*normpdf(a(j),e1,a1)+pw2*no rmpdf(a(j),e2,a2)); %¼ÆËãÃ¿¸öÑù±¾µã¶Ôw2µÄºóÑé¸ÅÂÊÒÔ»-Í¼ end figure(1) hold on plot(a,pw1_plot,'k-',a,pw2_plot,'r-') for k=1:m if result(k)==0 plot(x(k),-0.1,'b*')%Õý³£Ï¸°ûÓÃ*±íÊ¾ else end plot(x(k),-0.1,'rp')%Òì³£Ï¸°ûÓÃÎå½ÇÐÇ±íÊ¾ end legend('Õý³£Ï¸°ûºóÑé¸ÅÂÊÇúÏß','Òì³£Ï¸°ûºóÑé¸ÅÂÊÇúÏß','Õý³£Ï¸°û','Òì³£ Ï¸°û') xlabel('Ñù±¾Ï¸°ûµÄ¹Û²ìÖµ') ylabel('ºóÑé¸ÅÂÊ')

大连东软信息学院 grid on return; 电子工程系 function[R1_x,R2_x,result]=danger(x,pw1,pw2) m=numel(x);%得到待测细胞个数 R1_x=zeros(1,m);%存放把样本X判为正常细胞所造成的整体损失 R2_x=zeros(1,m);%存放把样本X判为异常细胞所造成的整体损失 -0.9780 -0.7932 -3.4549 1.1882 -1.1186 -3.0752 3.0682 4.2532 ] -2.2692 0.7932 -0.4221 -3.5549 -3.7287 2.8792 -1.4885 -3.5414 -0.9780 -0.7431 result=zeros(1,m);%存放比较结果矩阵 x = [-3.9847 -1.2401 -2.8531 -2.7605 -3.9934 -1.5799 disp(x) pw1 = 0.9 pw2 = 0.1 e1=-2; a1=0.5; e2=2; a2=2; %类条件概率分布 r11=0; r12=2; r21=4; r22=0; %风险决策表 %类条件概率服从正态分布 for i=1:m %计算两类风险值 R1_x(i)=r11*pw1*normpdf(x(i),e1,a1)/(pw1*normpdf(x(i),e1,a 1)+pw2*normpdf(x(i),e2,a2))+r21*pw2*normpdf(x(i),e2,a2)/(p w1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e2,a2)); R2_x(i)=r12*pw1*normpdf(x(i),e1,a1)/(pw1*normpdf(x(i),e1,a 1)+pw2*normpdf(x(i),e2,a2))+r22*pw2*normpdf(x(i),e2,a2)/(p

大连东软信息学院电子工程系 w1*normpdf(x(i),e1,a1)+pw2*normpdf(x(i),e2,a2)); end for i=1:m if R2_x(i)>R1_x(i)%第二类比第一类风险大 result(i)=0;%正常细胞 else result(i)=1;%异常细胞 end end a=[-5:0.05:5];%取样本点以画图 n=numel(a); R1_plot=zeros(1,n); R2_plot=zeros(1,n); for j=1:n R1_plot(j)=r11*pw1*normpdf(a(j),e1,a1)/(pw1*normpdf(a(j),e 1,a1)+pw2*normpdf(a(j),e2,a2))+r21*pw2*normpdf(a(j),e2,a2) /(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j),e2,a2)); %计算每个样本点对w1的后验概率以画图 R2_plot(j)=r12*pw1*normpdf(a(j),e1,a1)/(pw1*normpdf(a(j),e 1,a1)+pw2*normpdf(a(j),e2,a2))+r22*pw2*normpdf(a(j),e2,a2) /(pw1*normpdf(a(j),e1,a1)+pw2*normpdf(a(j),e2,a2)); %计算每个样本点对w2的后验概率以画图 end figure(1) hold on plot(a,R1_plot,'b-',a,R2_plot,'g*-') for k=1:m if result(k)==0 plot(x(k),-0.1,'b^')%正常细胞用上三角表示 else plot(x(k),-0.1,'go')%异常细胞用五角星表示 end end

资料库

模式识别实验二.doc

相关推荐

人工智能

热门标签

最新资料