很好的控制工程实验报告，只需稍加修改就可直接用.doc-资料库

qiandaosanren-1092578-4744300845181062666.doc.pdf-第1页.png

第1页 / 共21页

qiandaosanren-1092578-4744300845181062666.doc.pdf-第2页.png

第2页 / 共21页

qiandaosanren-1092578-4744300845181062666.doc.pdf-第3页.png

第3页 / 共21页

qiandaosanren-1092578-4744300845181062666.doc.pdf-第4页.png

第4页 / 共21页

qiandaosanren-1092578-4744300845181062666.doc.pdf-第5页.png

第5页 / 共21页

qiandaosanren-1092578-4744300845181062666.doc.pdf-第6页.png

第6页 / 共21页

qiandaosanren-1092578-4744300845181062666.doc.pdf-第7页.png

第7页 / 共21页

qiandaosanren-1092578-4744300845181062666.doc.pdf-第8页.png

第8页 / 共21页

《机械控制基础》实验指导书浙江师范大学交通学院机械电子系 2008 年 4 月

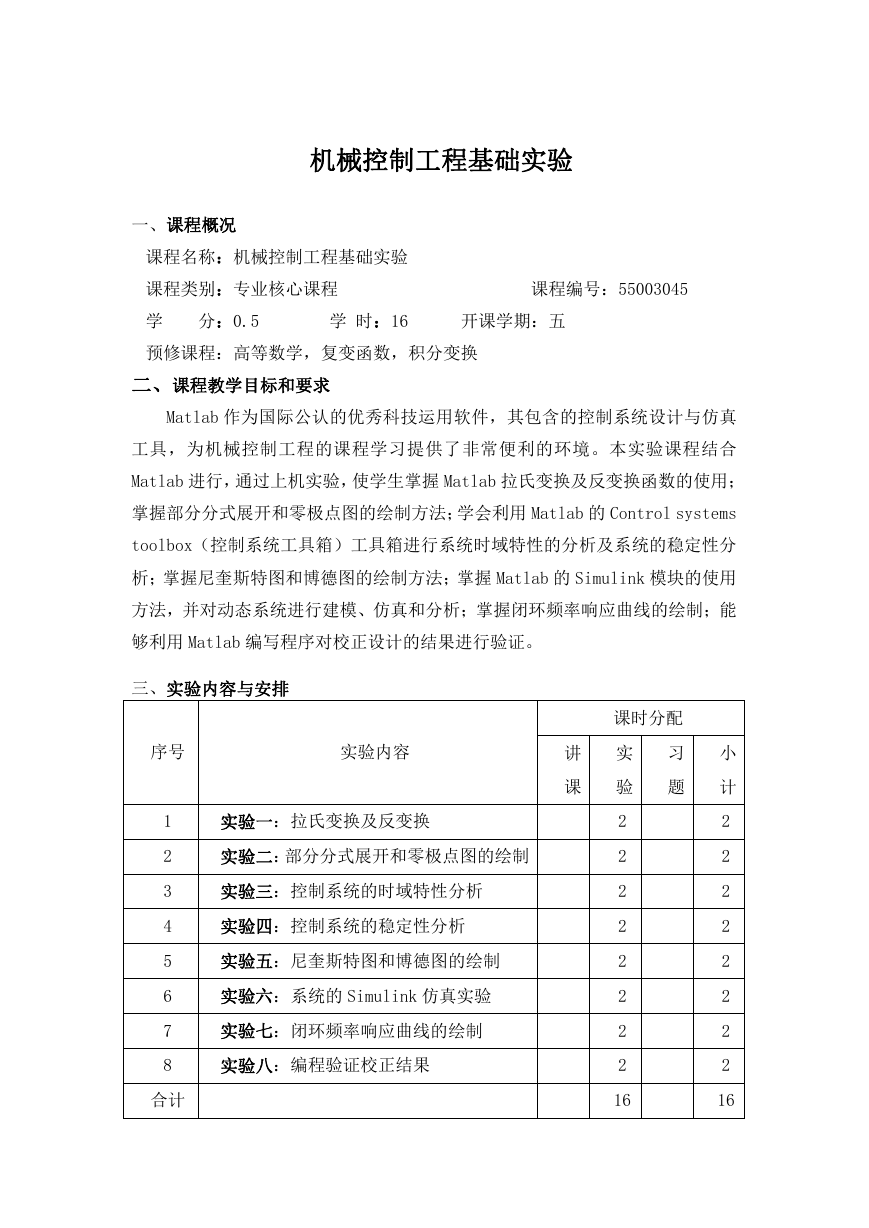
机械控制工程基础实验一、课程概况课程名称：机械控制工程基础实验课程类别：专业核心课程课程编号：55003045 学分：0.5 学时：16 开课学期：五预修课程：高等数学，复变函数，积分变换二、课程教学目标和要求 Matlab 作为国际公认的优秀科技运用软件，其包含的控制系统设计与仿真工具，为机械控制工程的课程学习提供了非常便利的环境。本实验课程结合 Matlab 进行，通过上机实验，使学生掌握 Matlab 拉氏变换及反变换函数的使用；掌握部分分式展开和零极点图的绘制方法；学会利用 Matlab 的 Control systems toolbox（控制系统工具箱）工具箱进行系统时域特性的分析及系统的稳定性分析；掌握尼奎斯特图和博德图的绘制方法；掌握 Matlab 的 Simulink 模块的使用方法，并对动态系统进行建模、仿真和分析；掌握闭环频率响应曲线的绘制；能够利用 Matlab 编写程序对校正设计的结果进行验证。三、实验内容与安排序号实验内容实验一：拉氏变换及反变换实验二：部分分式展开和零极点图的绘制实验三：控制系统的时域特性分析实验四：控制系统的稳定性分析实验五：尼奎斯特图和博德图的绘制实验六：系统的 Simulink 仿真实验实验七：闭环频率响应曲线的绘制实验八：编程验证校正结果 1 2 3 4 5 6 7 8 合计课时分配讲课实验习题小计 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 16 16

四、主要参考书目 [1] 王积伟吴振顺主编，《控制工程基础》.高等教育出版社，2005. [2] 王积伟张祖顺等主编，《控制工程基础学习指导与习题详解》.高等教育出版社，2005. [3] 董玉红杨清梅，《机械控制工程基础》.哈尔滨工业大学出版社，2003 [4] 杨叔子《机械工程控制基础》.华中科技大学出版社，2005 [5] 刘坤《Matlab 自动控制原理习题精解》.国防工业出版社，2005 五、实验考核方式实验考核：独立完成全部平时实验，取得课程总成绩的 30％。六、编制人签名：审核人签名：

实验一：拉氏变换及反变换一、实验目的 1．掌握 Matlab 的使用方法。 2．能够使用 Matlab 对时域函数进行拉氏变换与反变换。二、实验内容 1．计算时域函数 (2  e ( ) t  f 1 13 3 t  3sin 2 t  2cos 2 ) t 的拉氏变换。 2．计算时域函数 2 3)( s ( ) F s   s ( 的拉氏反变换。 2  4) 三、实验原理在Matlab的符号工具箱中，有拉氏变换和拉氏反变换的运算函数，及有关定义变量，表达式简化等的函数，下面作简单介绍。函数功能调用格式备注 1aplace 拉氏变换 L＝1aplace(F) ilaPLace 拉氏反变换 F＝ilaplace(L) Simple（简单）简化函数 simple(S) Pretty（美化）显示打印函数 Pretty(S) F是时域函数表达式，约定的自变量是t，得到的拉氏变换函数是L(s) L是拉氏函数 F是时域函数四、实验方法与步骤 1）计算时域函数 f ( ) t 1 13 进入Matlab环境   3 t (2 e  3sin 2 t  2cos 2 ) t 的拉氏变换。输入实验程序如下： >> syms t y; >> y=laplace(1/13 *(2*exp(-3*t)+3*sin(2*t)-2*cos(2*t))),b=simple(y) 得到运行结果： y =

2/13/(s+3)+6/13/(s^2+4)-2/13*s/(s^2+4) b = 2/(s+3)/(s^2+4) >> pretty(b) 2 3)( s ( s  2  4) 2）计算时域函数 ( ) F s  2 3)( s ( s  2  4) 的拉氏反变换输入实验程序如下： >> syms s; >> y=ilaplace(2/(s+3)/(s^2+4)),simple(y) 得到运行结果： y = 2/13*exp(-3*t)-2/13*cos(4^(1/2)*t)+3/26*4^(1/2)*sin(4^(1/2)*t) simplify: 2/13*exp(-3*t)+3/13*sin(2*t)-2/13*cos(2*t) 五、实验要求 1．验证Matlab拉氏变换与反变换函数 2．掌握拉氏变换与反变换的方法六、场地、设备与器材计算机及Matlab平台

实验二：部分分式展开和零极点图的绘制一实验目的 1．掌握使用Matlab进行部分分式展开的方法 3．掌握使用Matlab绘制零极点图的方法二实验内容 1．已知系统传递函数为： ( ) G s  1 5 s 2 s   20 试求系统的部分分式展开，并绘制系统的零极点图。 2．已知系统传递函数为： ( ) G s  2 8 s 12  s  3 24 s 47  16  2 s  4 s 60 s 试绘制系统的零极点图。三实验原理 Matlab提供了函数residue(留数)求解有理分式的部分分式展开，pzmap在复平面内绘制系统的零极点图，其应用格式为：功能函数 residue 求解有理分式的部分分式展开 pzmap 在复平面内绘制出系统的零极点图备注调用格式 [r,p,k]=residue(b,a) 其中b和a分别表示降幂排列的该有理分式的分子和分母多项式系数；r是求得的部分分式展开的各分子系数，p是系统极点，k是常数项得到以传递函数 Pzmap(num,den) ( ) G s  ( ) num s ( ) den s 表示的系统零极点图。其中num和den分别表示降幂排列的该有理分式的分子和分母多项式系数。四实验方法与步骤 1）实验程序为： >> b=[1]; >> a=[1,5,20]; >> [r,p,k]=residue(b,a)

运算结果为： r = p = 0 - 0.1348i 0 + 0.1348i -2.5000 + 3.7081i -2.5000 - 3.7081i k = [] 绘制系统零极点图程序： >> num=[1]; >> den=[1,5,20]; >> pzmap(num,den) 运行结果如下左图： 2）实验程序为： >> num=[8,24,16]; >> den=[1,12,47,60,0]; >> pzmap(num,den) 运行结果如上右图：五实验要求 1．对（2）式进行部分分式展开。 2．思考零极点分布对系统性能的影响。六实验设备计算机及Matlab平台

实验三：控制系统的时域特性分析一实验目的 1．掌握线性定常系统动态性能指标的测试方法。 2．研究线性定常系统的参数对其动态性能和稳定性的影响。 3. 能够使用Matlab计算系统对典型输入的响应，绘制响应曲线。二实验内容 1. 学习 Matlab 函数的使用方法 2. 使用 Matlab 编程求解一阶系统对典型输入的响应，绘制响应曲线 3. 分别使二阶系统的ζ=0，0<ζ<1，ζ＝1，ζ<0 和ζ>1，使用Matlab绘制其响应曲线。一阶系统闭环传递函数为 1 Ts  二阶系统开环传递函数为 ( ) G s  1 ( ) G s  2 s  2  n 2 2   n  s n 三实验原理本实验研究一阶，二阶系统的动态响应。控制系统最常用的时域分析方法是，当输入信号为单位阶跃和单位脉冲函数时，求出系统的输出响应，分别称为单位阶跃响应和单位脉冲响应。在 Matlab 中，求取连续系统的单位阶跃响应函数 step（阶梯），单位脉冲响应函数 impulse（脉冲），零输入响应函数 initial（初始）。其调用格式如下表所示：函数 step 求阶跃响应求脉冲响应 impulse initial 求连续系统的零输入响应功能调用格式 [y,x]=step(num,den,t) [y,x]=impulse(num,den,t) [y,x,t]=initial(a,b,c,d,x0) 四实验方法与步骤 1．分别计算一阶系统对输入信号（单位阶跃函数，单位脉冲函数）在初始状态为零时的时间响应。求系统对单位阶跃输入的响应。当取 T 值为 1 时，程序如下：

资料库

很好的控制工程实验报告，只需稍加修改就可直接用.doc

相关推荐

课程资源

热门标签

最新资料