logo资料库

蒋玉龙半导体器件原理 PPT.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：11.76M 资料格式：pdf 举报 版权申诉
第1页 / 共366页
第2页 / 共366页
第3页 / 共366页
第4页 / 共366页
第5页 / 共366页
第6页 / 共366页
第7页 / 共366页
第8页 / 共366页
资料共366页，剩余部分请下载后查看
    L01-pn结的频率特性与开关特性
    半导体器件原理
    第一章 pn结的频率特性与开关特性
    1.1 半物要点回顾1
    幻灯片编号 4
    幻灯片编号 5
    幻灯片编号 6
    幻灯片编号 7
    第一章 pn结的频率特性与开关特性
    幻灯片编号 9
    幻灯片编号 10
    幻灯片编号 11
    幻灯片编号 12
    幻灯片编号 13
    幻灯片编号 14
    幻灯片编号 15
    幻灯片编号 16
    第一章 pn结的频率特性与开关特性
    幻灯片编号 18
    幻灯片编号 19
    幻灯片编号 20
    幻灯片编号 21
    幻灯片编号 22
    L02-双极型晶体管
    半导体器件原理
    第二章 双极型晶体管
    幻灯片编号 3
    幻灯片编号 4
    幻灯片编号 5
    第二章 双极型晶体管
    2.2 电流放大原理1
    幻灯片编号 8
    幻灯片编号 9
    幻灯片编号 10
    第二章 双极型晶体管
    幻灯片编号 12
    幻灯片编号 13
    幻灯片编号 14
    幻灯片编号 15
    幻灯片编号 16
    幻灯片编号 17
    幻灯片编号 18
    幻灯片编号 19
    幻灯片编号 20
    幻灯片编号 21
    幻灯片编号 22
    幻灯片编号 23
    幻灯片编号 24
    幻灯片编号 25
    幻灯片编号 26
    幻灯片编号 27
    幻灯片编号 28
    幻灯片编号 29
    幻灯片编号 30
    幻灯片编号 31
    幻灯片编号 32
    幻灯片编号 33
    幻灯片编号 34
    幻灯片编号 35
    幻灯片编号 36
    幻灯片编号 37
    幻灯片编号 38
    幻灯片编号 39
    幻灯片编号 40
    幻灯片编号 41
    第二章 双极型晶体管
    幻灯片编号 43
    幻灯片编号 44
    幻灯片编号 45
    幻灯片编号 46
    幻灯片编号 47
    幻灯片编号 48
    幻灯片编号 49
    幻灯片编号 50
    幻灯片编号 51
    第二章 双极型晶体管
    幻灯片编号 53
    幻灯片编号 54
    幻灯片编号 55
    幻灯片编号 56
    第二章 双极型晶体管
    幻灯片编号 58
    幻灯片编号 59
    幻灯片编号 60
    幻灯片编号 61
    幻灯片编号 62
    幻灯片编号 63
    幻灯片编号 64
    幻灯片编号 65
    幻灯片编号 66
    幻灯片编号 67
    幻灯片编号 68
    幻灯片编号 69
    幻灯片编号 70
    幻灯片编号 71
    幻灯片编号 72
    幻灯片编号 73
    幻灯片编号 74
    幻灯片编号 75
    幻灯片编号 76
    幻灯片编号 77
    幻灯片编号 78
    幻灯片编号 79
    幻灯片编号 80
    幻灯片编号 81
    幻灯片编号 82
    幻灯片编号 83
    幻灯片编号 84
    幻灯片编号 85
    幻灯片编号 86
    幻灯片编号 87
    幻灯片编号 88
    幻灯片编号 89
    幻灯片编号 90
    幻灯片编号 91
    幻灯片编号 92
    幻灯片编号 93
    幻灯片编号 94
    幻灯片编号 95
    幻灯片编号 96
    幻灯片编号 97
    幻灯片编号 98
    幻灯片编号 99
    幻灯片编号 100
    幻灯片编号 101
    幻灯片编号 102
    幻灯片编号 103
    幻灯片编号 104
    幻灯片编号 105
    幻灯片编号 106
    幻灯片编号 107
    幻灯片编号 108
    幻灯片编号 109
    幻灯片编号 110
    幻灯片编号 111
    幻灯片编号 112
    幻灯片编号 113
    幻灯片编号 114
    幻灯片编号 115
    幻灯片编号 116
    第二章 双极型晶体管
    幻灯片编号 118
    幻灯片编号 119
    幻灯片编号 120
    幻灯片编号 121
    幻灯片编号 122
    幻灯片编号 123
    幻灯片编号 124
    幻灯片编号 125
    幻灯片编号 126
    幻灯片编号 127
    幻灯片编号 128
    幻灯片编号 129
    幻灯片编号 130
    幻灯片编号 131
    幻灯片编号 132
    幻灯片编号 133
    幻灯片编号 134
    幻灯片编号 135
    幻灯片编号 136
    幻灯片编号 137
    幻灯片编号 138
    幻灯片编号 139
    幻灯片编号 140
    幻灯片编号 141
    幻灯片编号 142
    幻灯片编号 143
    幻灯片编号 144
    幻灯片编号 145
    幻灯片编号 146
    幻灯片编号 147
    幻灯片编号 148
    幻灯片编号 149
    L03-MOSFET的基本特性
    半导体器件原理
    第三章 MOSFET的基本特性
    幻灯片编号 3
    幻灯片编号 4
    幻灯片编号 5
    幻灯片编号 6
    幻灯片编号 7
    幻灯片编号 8
    幻灯片编号 9
    幻灯片编号 10
    幻灯片编号 11
    幻灯片编号 12
    第三章 MOSFET的基本特性
    幻灯片编号 14
    幻灯片编号 15
    幻灯片编号 16
    幻灯片编号 17
    幻灯片编号 18
    幻灯片编号 19
    幻灯片编号 20
    幻灯片编号 21
    幻灯片编号 22
    幻灯片编号 23
    幻灯片编号 24
    幻灯片编号 25
    幻灯片编号 26
    幻灯片编号 27
    幻灯片编号 28
    幻灯片编号 29
    幻灯片编号 30
    幻灯片编号 31
    幻灯片编号 32
    第三章 MOSFET的基本特性
    幻灯片编号 34
    幻灯片编号 35
    幻灯片编号 36
    幻灯片编号 37
    幻灯片编号 38
    幻灯片编号 39
    幻灯片编号 40
    幻灯片编号 41
    幻灯片编号 42
    幻灯片编号 43
    幻灯片编号 44
    幻灯片编号 45
    幻灯片编号 46
    幻灯片编号 47
    幻灯片编号 48
    幻灯片编号 49
    幻灯片编号 50
    幻灯片编号 51
    幻灯片编号 52
    幻灯片编号 53
    幻灯片编号 54
    幻灯片编号 55
    幻灯片编号 56
    幻灯片编号 57
    幻灯片编号 58
    幻灯片编号 59
    幻灯片编号 60
    幻灯片编号 61
    幻灯片编号 62
    幻灯片编号 63
    幻灯片编号 64
    幻灯片编号 65
    幻灯片编号 66
    幻灯片编号 67
    幻灯片编号 68
    幻灯片编号 69
    幻灯片编号 70
    幻灯片编号 71
    幻灯片编号 72
    幻灯片编号 73
    幻灯片编号 74
    幻灯片编号 75
    幻灯片编号 76
    幻灯片编号 77
    幻灯片编号 78
    幻灯片编号 79
    幻灯片编号 80
    幻灯片编号 81
    幻灯片编号 82
    幻灯片编号 83
    幻灯片编号 84
    幻灯片编号 85
    幻灯片编号 86
    幻灯片编号 87
    幻灯片编号 88
    幻灯片编号 89
    第三章 MOSFET的基本特性
    幻灯片编号 91
    幻灯片编号 92
    幻灯片编号 93
    幻灯片编号 94
    幻灯片编号 95
    幻灯片编号 96
    幻灯片编号 97
    幻灯片编号 98
    幻灯片编号 99
    幻灯片编号 100
    幻灯片编号 101
    幻灯片编号 102
    幻灯片编号 103
    第三章 MOSFET的基本特性
    幻灯片编号 105
    幻灯片编号 106
    幻灯片编号 107
    幻灯片编号 108
    幻灯片编号 109
    幻灯片编号 110
    幻灯片编号 111
    幻灯片编号 112
    幻灯片编号 113
    幻灯片编号 114
    幻灯片编号 115
    幻灯片编号 116
    幻灯片编号 117
    第三章 MOSFET的基本特性
    幻灯片编号 119
    幻灯片编号 120
    幻灯片编号 121
    L04-小尺寸MOSFET的特性
    半导体器件原理
    第四章 小尺寸MOSFET的特性
    幻灯片编号 3
    幻灯片编号 4
    幻灯片编号 5
    幻灯片编号 6
    幻灯片编号 7
    幻灯片编号 8
    幻灯片编号 9
    幻灯片编号 10
    幻灯片编号 11
    幻灯片编号 12
    幻灯片编号 13
    幻灯片编号 14
    幻灯片编号 15
    幻灯片编号 16
    幻灯片编号 17
    幻灯片编号 18
    幻灯片编号 19
    幻灯片编号 20
    幻灯片编号 21
    幻灯片编号 22
    幻灯片编号 23
    幻灯片编号 24
    幻灯片编号 25
    幻灯片编号 26
    幻灯片编号 27
    幻灯片编号 28
    幻灯片编号 29
    幻灯片编号 30
    第四章 小尺寸MOSFET的特性
    幻灯片编号 32
    幻灯片编号 33
    幻灯片编号 34
    幻灯片编号 35
    幻灯片编号 36
    幻灯片编号 37
    幻灯片编号 38
    幻灯片编号 39
    幻灯片编号 40
    幻灯片编号 41
    幻灯片编号 42
    幻灯片编号 43
    幻灯片编号 44
    第四章 小尺寸MOSFET的特性
    幻灯片编号 46
    幻灯片编号 47
    幻灯片编号 48
    幻灯片编号 49
    幻灯片编号 50
    幻灯片编号 51
    幻灯片编号 52
    幻灯片编号 53
    幻灯片编号 54
    幻灯片编号 55
    幻灯片编号 56
    幻灯片编号 57
    幻灯片编号 58
    幻灯片编号 59
    幻灯片编号 60
    幻灯片编号 61
    幻灯片编号 62
    幻灯片编号 63
    幻灯片编号 64
    幻灯片编号 65
    幻灯片编号 66
    幻灯片编号 67
    幻灯片编号 68
    幻灯片编号 69
    幻灯片编号 70
    幻灯片编号 71
    幻灯片编号 72
    幻灯片编号 73
    幻灯片编号 74
    半导体器件原理 1/22 主讲人：蒋玉龙 本部微电子学楼312室，65643768 Email: yljiang@fudan.edu.cn http://10.14.3.121
    第一章 pn结的频率特性与开关特性 2/22 1.1 半物要点回顾 1.2 pn结的频率特性 1.3 pn结的开关特性
    1.1 半物要点回顾1 3/22 ( E C ( E F F − − E E V ) ) ]kT ]kT  J = J s exp       qV kT  −   1    d 耗尽 =    02 rεε q V D V − N 2/1    ( qV kT ) − ] 1 exp ( − Lx )p 重要公式 = =  V   C J J N N [ n exp − 0 [ p exp − 0 dn qD n =扩 n dx E qn µ=漂 n n dp qD −=扩 p dx E qp µ=漂 p [ exp J J = p p p n 0 xp )( ∆
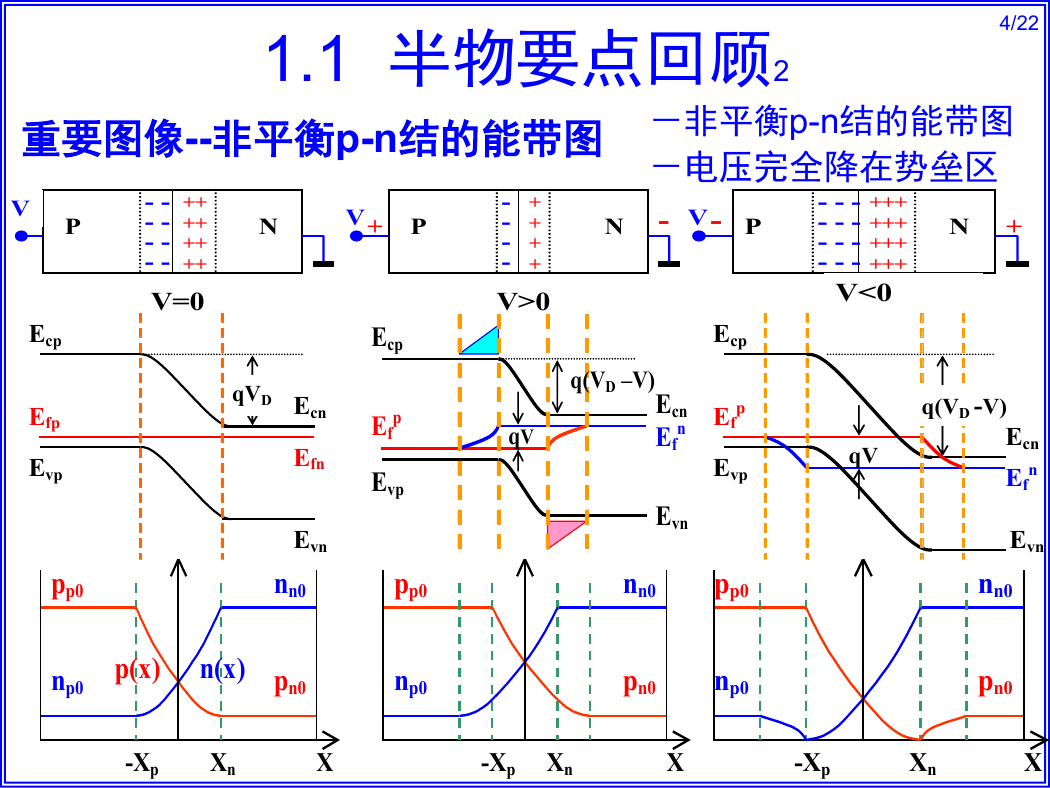
    1.1 半物要点回顾2 4/22 重要图像--非平衡p-n结的能带图 V N V + P －非平衡p-n结的能带图 －电压完全降在势垒区 - + V N - P N - + - + - + - + V>0 - - - - - - - - - - - - +++ +++ +++ +++ V<0 Ecp q(VD –V) Ecn n Ef qV Evn nn0 pn0 p Ef Evp pp0 np0 q(VD -V) Ecn n Ef qV Evn nn0 pn0 P Ecp Efp Evp pp0 np0 - - ++ - - ++ - - ++ - - ++ V=0 qVD Ecn Efn Evn nn0 p(x) n(x) pn0 Ecp p Ef Evp pp0 np0 -Xp Xn X -Xp Xn X -Xp Xn X
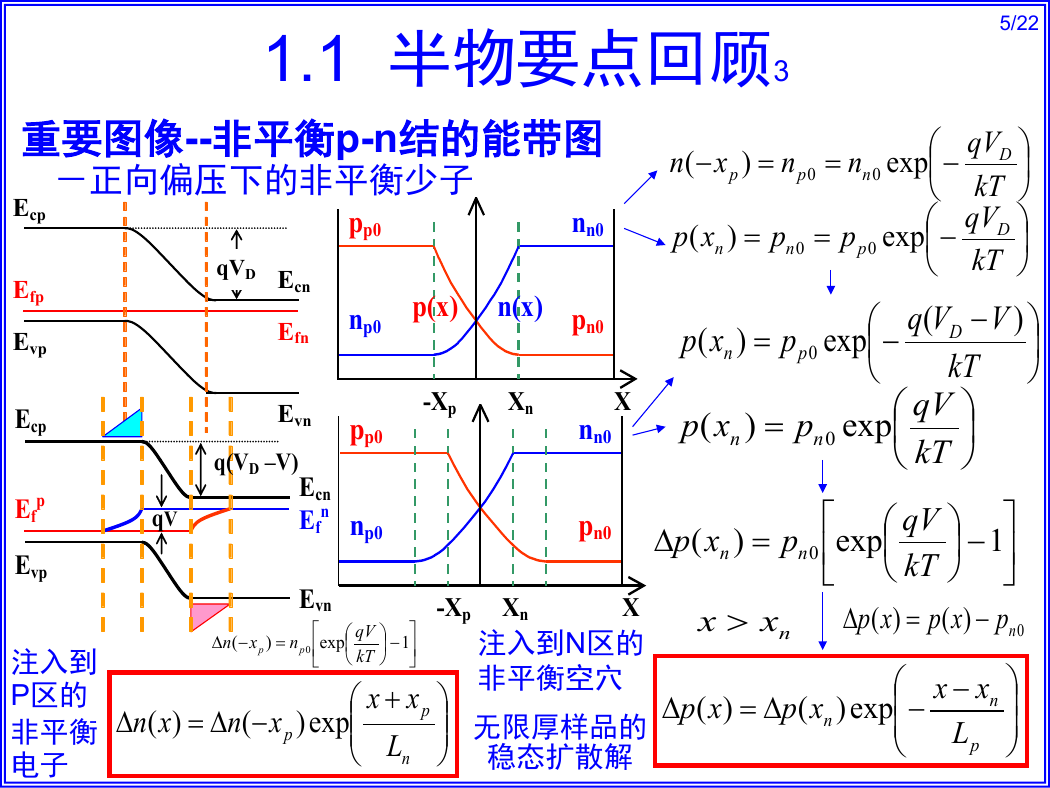
    1.1 半物要点回顾3 5/22 重要图像--非平衡p-n结的能带图 Ecp －正向偏压下的非平衡少子 pp0 nn0 n ( − x p ) = n p 0 = n n 0 xp ( n ) = p n 0 = p p 0 exp exp       )    qV − D  kT  qV − D  kT  Vq V ( − D kT    qV kT exp −    exp xp ( n ) = p n 0 xp ( ∆ n ) = p n 0    x > nx    qV kT = exp    xp )( ∆  −  xp )( − xp )( ∆ ∆= xp ( ) n   exp   − x − L p x  1   np     n 0 Efp Evp Ecp p Ef Evp 注入到 P区的 非平衡 电子 p(x) n(x) pn0 xp ( n ) = p p 0 qVD Ecn Efn Evn q(VD –V) Ecn n Ef qV np0 pp0 np0 -Xp Xn X nn0 pn0 n ( −∆ x ) = n p xn )( ∆ ( −∆= n x ) p Evn  exp   p 0  1   x qV   −  kT   x  +  exp L  n p    -Xp Xn X 注入到N区的 非平衡空穴 无限厚样品的 稳态扩散解
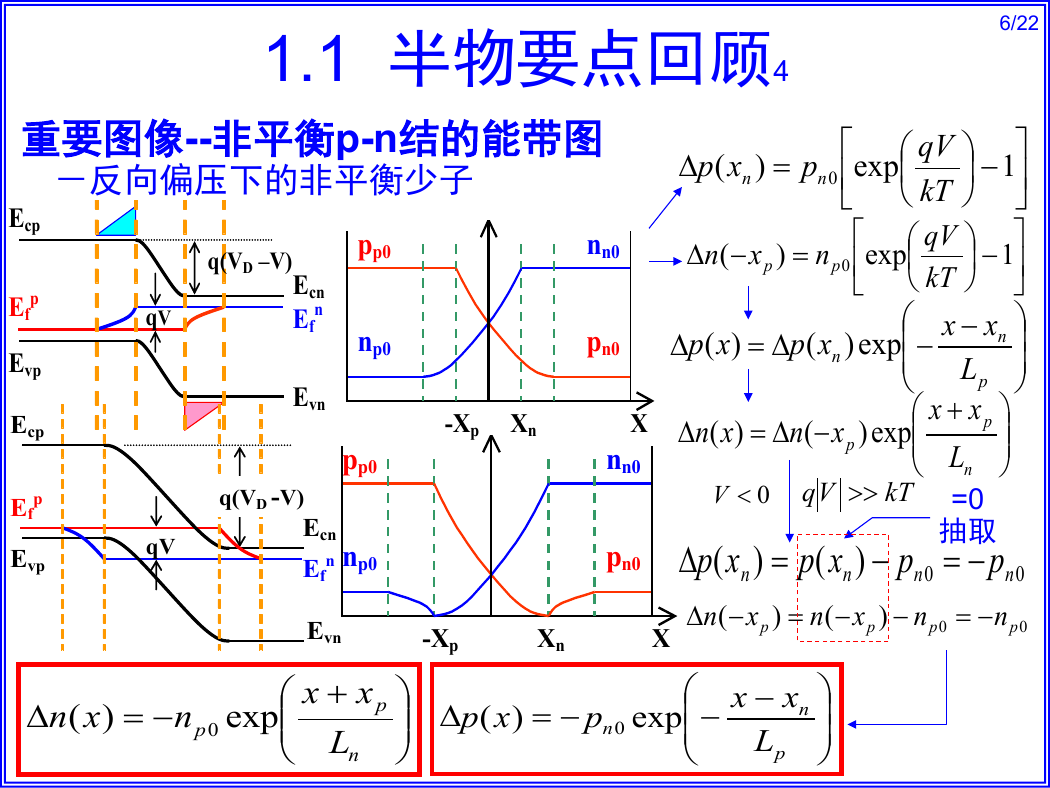
    1.1 半物要点回顾4 6/22 xp ( ∆ n ) = p n 0    n ( −∆ x ) = n p p 0    xp )( ∆ ∆= xp ( ) n xn )( ∆ ( −∆= n x p >> 0
    1.1 半物要点回顾5 pp0 np0 -Xp Xn J= Jp +Jn Jp 7/22 nn0 pn0 Jn Jp X X −  1   0p p n 0n p << ∆ n n << ∆ p 重要图像-- 理想p-n结的J-V关系 前提： －小注入 －突变耗尽层条件 （耗尽层外电中性） －忽略势垒区中载流子的产生、复合 －非简并 电流密度 J J J = p xp xp ( )( ∆ ∆= x ( p x ( n xp ( ∆ + + ) ) n ) + = ) n n n n J = = x x − L p −   exp   pd ∆ dx 2 qD n in NL n A | xx = + = n     J ( x n ) p −= qD p J s =     2 n qD ip NL p D 0 n p n ) n x 扩散电流组成 J x ( n J ( −    qV kT ) p qV  exp  kT   1   2 n i N  1   ( −  −   −  0 = n p    J n A x Jn ) = p -Xp Xn qD n L n    n p 0 exp    qV kT qV kT     −      1      J = J s exp p J J     qD L p p p n exp 0    2 n i N D p 0 = n
    第一章 pn结的频率特性与开关特性 8/22 1.1 半物要点回顾 1.2 pn结的频率特性 1.3 pn结的开关特性
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料