ADAMS函数学习..ppt

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.16M 资料格式：ppt 举报版权申诉

hello84-1883330-4744302542999448567.ppt.pdf-第1页.png

第1页 / 共16页

hello84-1883330-4744302542999448567.ppt.pdf-第2页.png

第2页 / 共16页

hello84-1883330-4744302542999448567.ppt.pdf-第3页.png

第3页 / 共16页

hello84-1883330-4744302542999448567.ppt.pdf-第4页.png

第4页 / 共16页

hello84-1883330-4744302542999448567.ppt.pdf-第5页.png

第5页 / 共16页

hello84-1883330-4744302542999448567.ppt.pdf-第6页.png

第6页 / 共16页

hello84-1883330-4744302542999448567.ppt.pdf-第7页.png

第7页 / 共16页

hello84-1883330-4744302542999448567.ppt.pdf-第8页.png

第8页 / 共16页

文本预览

• 冲击函数impact (c, ċ, c0, k, e, cmax, d) c : 两个对象之间的实际距离（可用距离函数DZ 等实现） ċ ：c 的一阶导数（可用速度函数VZ等实现） c0：确定碰撞力打开和关闭的触发距离，它应该是实常数 k ：刚度系数 e : 刚度指数 cmax 阻尼系数 d : 阻尼完全起作用的距离当 c >=c0 , Fimpact=off 当 c < c0 , Fimpact=on d必须是大于0的数？（不清楚怎么用，也不知道用在什么环境下）

• 线性的弹簧---阻尼关系式： ForceSPDP=-k(q-q0)-cq.+F0 q : 确定弹簧阻尼器的两个位置之间的距离 q.:沿两个位置之间连线方向的相对速度 k ：弹簧刚度系数（永远大于0） c : 粘性阻尼系数（永远大于0） F0 ：弹簧的参考力（预载） q0 : 参考长度（在预载位置，永远大于0）在ADAMS中，用户自定义方程是 -k(DM(I,J)-q0 )-c*VR(I,J)+F0

• 近似拟和法曲线函数AKISPL AKISPL（x , z , spline , iord） x : 确定x轴数值的独立变量 z : 可选参数，确定插值表面z轴数值的第二个独立变量 spline : 用于确定相关变量（y）与独立变量（x或z 一一对应关系的样条曲线） iord : 确定插值点阶数的整数变量（通常为0，也可以是1或2）例如 AKISPL（DM（I，J），0 , spline_1 , 0）注意：在创建AKISPL函数时，可以精确地创建 CUBSPL和CURVE函数；另外，当z为0时，iord可以省略，例如 f = AKISPL(DX(marker_1, marker_2, marker_2), 0, spline_1)

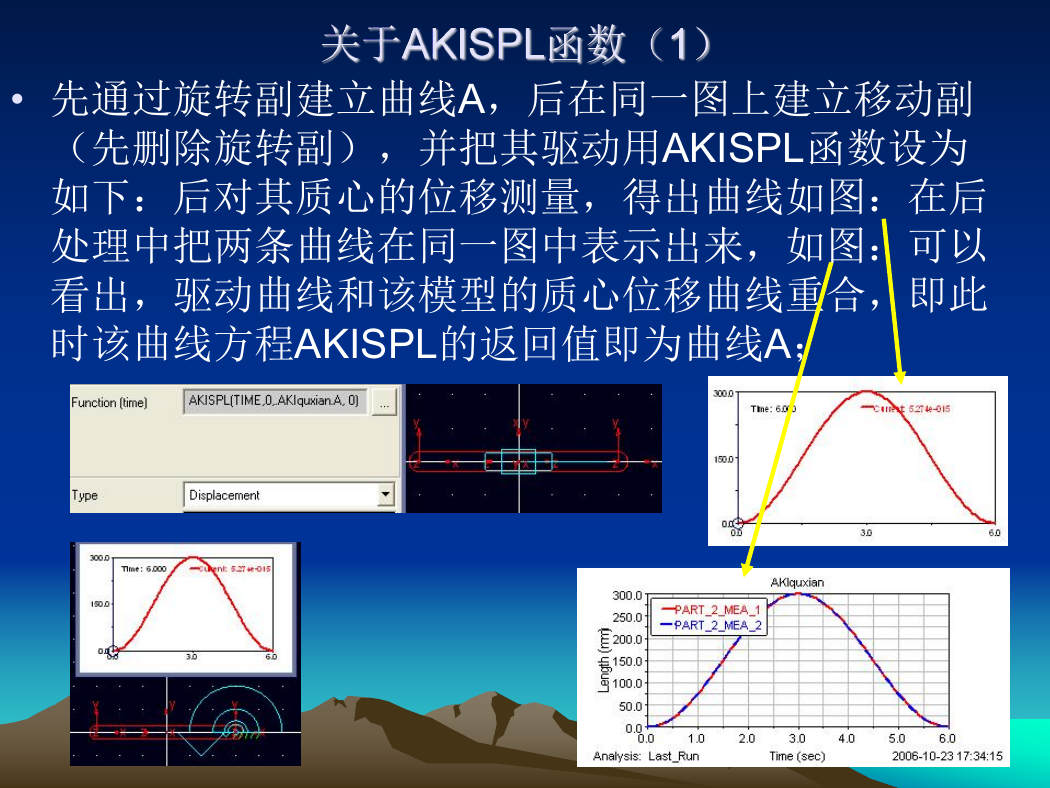
• 先通过旋转副建立曲线A，后在同一图上建立移动副（先删除旋转副），并把其驱动用AKISPL函数设为如下：后对其质心的位移测量，得出曲线如图：在后处理中把两条曲线在同一图中表示出来，如图：可以看出，驱动曲线和该模型的质心位移曲线重合，即此时该曲线方程AKISPL的返回值即为曲线A；

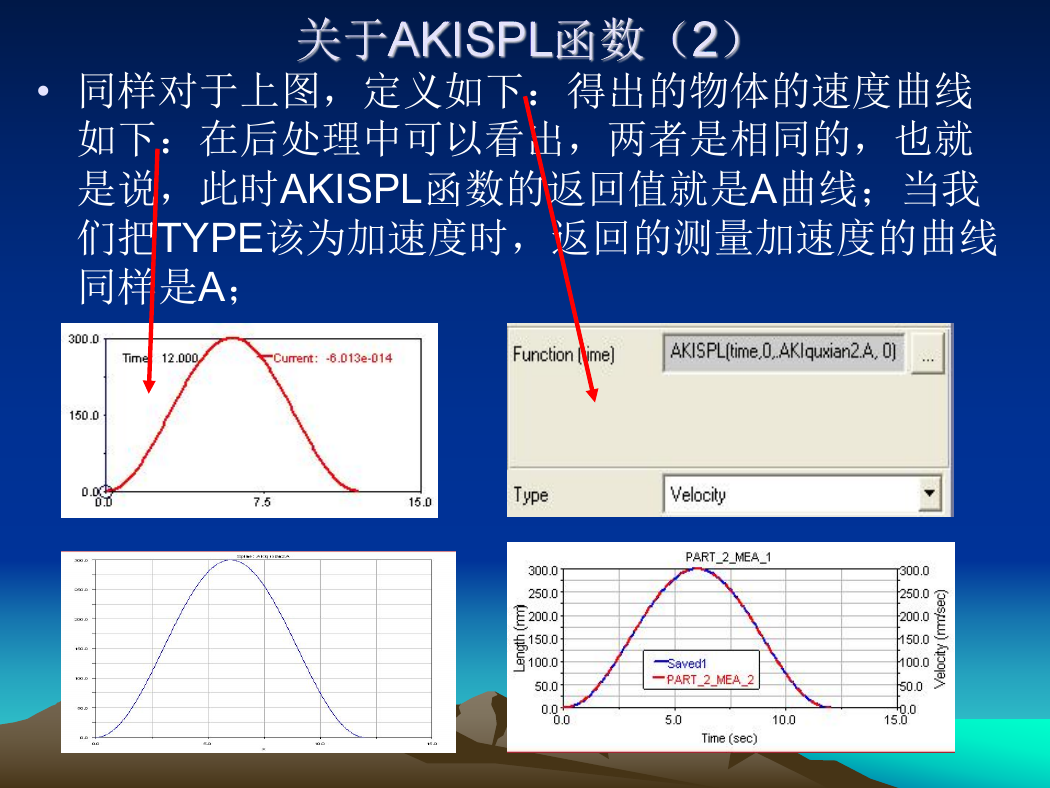
• 同样对于上图，定义如下：得出的物体的速度曲线如下：在后处理中可以看出，两者是相同的，也就是说，此时AKISPL函数的返回值就是A曲线；当我们把TYPE该为加速度时，返回的测量加速度的曲线同样是A；

• 使用Cubic样条函数（CUBSPL）在驱动中比 Akima样条函数要好 • 使用Akima样条函数（AKISPL）在力中比Cubic 样条函数要好 • Akima插值方法更快，并且可以定义为一个表面，但它的导数通常不连续 • 在IMPACT或者BISTOP函数中，不要使用1.0作为指数

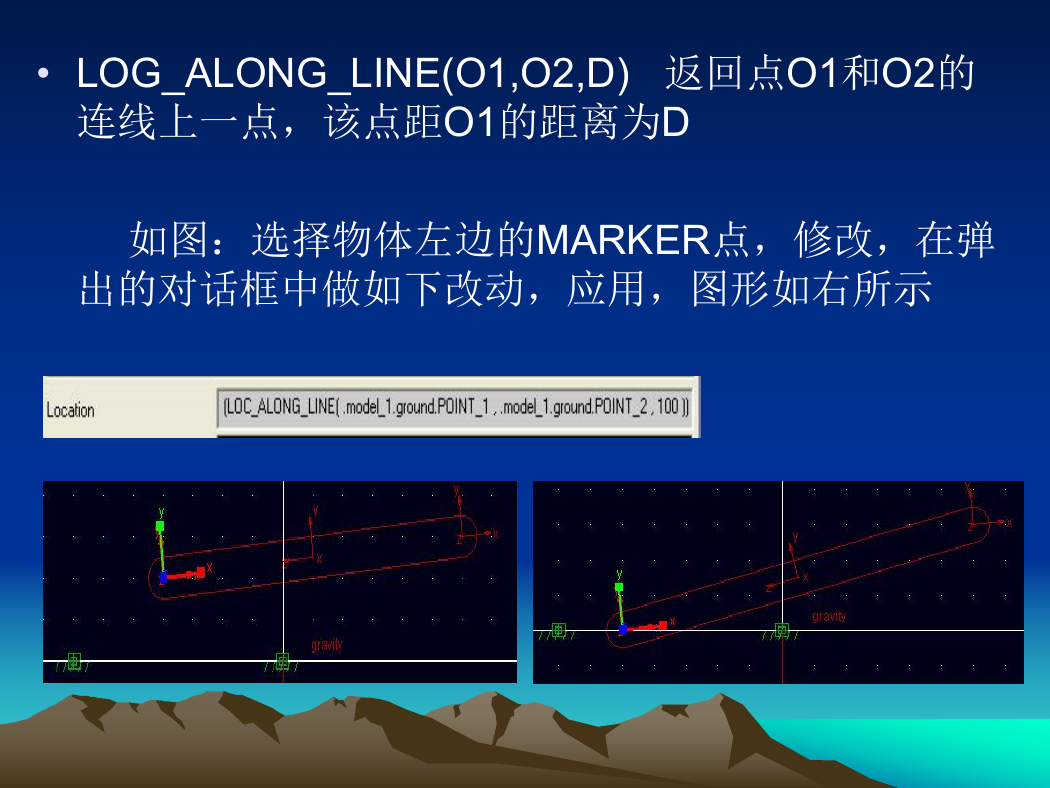
• LOG_ALONG_LINE(O1,O2,D) 返回点O1和O2的连线上一点，该点距O1的距离为D 如图：选择物体左边的MARKER点，修改，在弹出的对话框中做如下改动，应用，图形如右所示

• STEP函数 STEP(q,q1,f1,q2,f2) q : 独立的变量 q1 : 变量的初始值 f1 : 函数的初始值 q2 : 变量的终止值 f2 : 函数的终止值注意：定义函数时要求 q1 < q2 • STEP 有两种书写格式：　一种是嵌入式：STEP (x, x0, h0, x1, （STEP (x, x1, h1, x2, （STEP (x, x2, h2, x3, h2) ））））（当然你可以嵌套更多的）　另一种就是增量式：STEP (x, x0, h0, x1, h1)+STEP (x, x1, h2, x2, h3)+STEP (x, x2, h4, x3, h5)+……

分享到：

赞收藏

资料库

ADAMS函数学习..ppt

相关推荐

开发技术

热门标签

最新资料